Reduced-Order Observer-Based Leader-Following Formation Control for Discrete-Time Linear Multi-Agent Systems

Zhongxin Liu,,Yangbo Li,Fuyong Wang,and Zengqiang Chen

Abstract—Formation control of discrete-time linear multi-agent systems using directed switching topology is considered in this work via a reduced-order observer,in which a formation control protocol is proposed under the assumption that each directed communication topology has a directed spanning tree.By utilizing the relative outputs of neighboring agents,a reduced-order observer is designed for each following agent.A multi-step control algorithm is established based on the Lyapunov method and the modified discrete-time algebraic Riccati equation.A sufficient condition is given to ensure that the discrete-time linear multiagent system can achieve the expected leader-following formation.Finally,numerical examples are provided so as to demonstrate the effectiveness of the obtained results.

I.INTRODUCTION

FOR the last few years,a great deal of researchers have studied distributed coordination of groups of agents for their broad applications in many domains.As an important fundamental problem in cooperative control,the purpose of consensus control is to design appropriate control protocols such that all agents can reach the agreement value of their common states asymptotically or in finite time.Much effort has been taken to solve all sorts of distributed coordination control problems in the early literature,such with formation control [1]–[3],containment control [4]–[7],output regulation[8],the adaptive consensus problem [9]–[10],the state constraint consensus problem [11]–[12] etc.

In the existing literature,Lyapunov-based methods and stochastic matrices were commonly used in solving first-order[13]–[16] and second-order [17]–[22] consensus problems.In addition,the consensus problem of linear multi-agent systems has also been investigated in many literature [23]–[27].Compared to systems with continuous-time dynamics,discrete-time systems are much more suitable for realization using computer.Moreover,many practical systems cannot be characterized by continuous dynamics.Some interesting issues on consensus stability of discrete-time multi-agent systems have been investigated in [28]–[32].

Most literature mentioned above assume that agents could measure the state information of their neighbours through communication channels unerringly.However,for many practical systems,the agents can only measure the output information of their neighbors due to an unreliable communication environment or other reason,full state information is thus not always available.For such consensus problems,a common method is to propose suitable observers so as to estimate these unmeasurable variables.In [17],owing to the unpredictable speed of the leader,an estimation law was adopted using first-order followers to estimate the leader's state.An observer-based consensus strategy for a second-order system lacking a velocity measurement was proposed in [18].Based on the relative outputs of the neighbours,observer-type consensus protocols were presented in [23],which can solve consensus problem for linear networked systems.In many practical systems,switching is a common phenomenon.For example,those systems with abrupt parameter variations can be modelled as switched systems.The leader-following consensus problem of linear systems with state-observer under one group of directed switching topologies was investigated in [24],and the conclusion of [24] was then extended in [30] to discretetime systems.In [31],two consensus problems for discrete-time multi-agent systems with switching network topology were studied,and the consensus problem for discrete-time linear multi-agent systems under directed switching networks was investigated in [32].In [33],the authors investigated the consensus problem with linear multi-agent systems by adopting a new reduced-order observer.Based on [33],the leaderfollowing multi-agent consensus problem was investigated in[34] by designing a reduced-order observer for each following agent.For a system with discrete-time linear dynamics,a distributed reduced-order observer-based consensus control law was given in [35].

With the development of consensus theory,its application by researchers trying to solve formation control issues has increased.By converting formation control problems for networked systems into consensus-like problems,the tools in consensus theory can be used in dealing with subsequent problems.It has been proposed in [36] that many existing leaderfollowing,virtual leader,and behavioural formation control methods can be integrated in the general framework of consensus protocol establishment.Some necessary and sufficient graphical conditions for formation control of unicycles were obtained in [37].In [38],a behavior-based method was proposed to realize complex formation for multirobots.A new formation control approach based on the distances among the networked robots modeled as single integrators was provided in [39].For general linear multi-agent systems with switching directed topologies,the time-varying formation control was investigated in [40] and the time-varying output formation control was studied in [41].By using an adaptive based method,a distributed time-varying formation control strategy for multi-agent systems with high-order linear dynamics was investigated in [42].For leader-to-formation stability of multi-agent systems,an adaptive optimal control approach was proposed in [43].Considering the same communication problems as above-mentioned,many issues of observer-based formation control problems have been studied recently.A learning-based model predictive control (LBMPC)algorithm was presented in [3] for formation flight control of multiple vehicles systems.In [2],by introducing linear extended state observer,a formation control strategy was provided for the case where the velocity of the neighboring agent is unmeasurable.The leader-following formation problem for a multi-robot system was studied in [1],in which the leader agent is unknown to the followers.

So far,the bulk of existing literature on observer-based formation control has been largely focused on continuoustime systems.Motivated by the above works,especially by[33] and [34],we consider the leader-following formation control problem for discrete-time linear multi-agent systems through using a reduced-order observer-based strategy.The main contributions of this work are summarized as follows:1)Under directed switching topology,the leader-following formation control problem for discrete-time linear multi-agent systems is first considered in this work;2) A novel reducedorder observer is designed for each following agent based on the relative output information,which can estimate the state effectively;3) Based on the Lyapunov method and the modified discrete-time algebraic Riccati equation,a multi-step control algorithm is established for achieving the expected leader-following formation.

A.Notation

Rm×n(or Cm×n) denotes the set ofm×nreal (or complex)matrices.ATrepresents the transpose of matrixA.Inis then×nidentity matrix,and 1n=[1,1,...,1]T.For a symmetric matrixP,whenP>0(<0,≥0,≤0),we say it is positive definite (negative definite,positive semi-definite,or negative semi-definite).‖·‖ denotes the Euclidean norm.|·| denotes the module of a complex number or the absolute value of a real number.⊗ denotes the Kronecker product.

II.PRELIMINARIES AND PROBLEM FORMULATION

Using graph theory,the interaction relationship amongNagents of a multi-agent system can be described by a directed graph G=(V,E,A).Here,V={ν1,ν2,...,νN} [den]otes the set of nodes and E ⊆V×V is the edge set.is the weighted adjacency matrix,which is defined such thatai j>0 if(vj,vi)∈E andai j=0 otherwise.It is assumed thataii=0,i∈Sr≜{1,2,...,N}.The Laplacian matrix L is defined asandlij=−aij,i≠j.A directed tree of a directed graph that is formed by the graph edges that connect from the root node to every other node in the graph is called a directed spanning tree.According to the definition,we can easily obtain that the Laplacian matrix L satisfies L1N=0.Now some basic lemmas are introduced in the following.

Lemma 1 [13]:The Laplacian matrix L is positive semidefinite and satisfies L1N=0.If a weighted digraphG contains a directed spanning tree,then the corresponding Laplacian matrix L has exactly one zero eigenvalue.

Lemma 2 [44]:A symmetric matrixScan be partitioned into the following block form

The following lemma is given to address the existence of solutions for the modified discrete-time algebraic Ricatti equation.

Lemma 3 [45]–[46]:If(A,B) is stabilizable and(A,Q12) is detectable,there exists a scalar δc∈[0,1) such that the discrete-time modified algebraic Riccati equation (1) has a unique positive definite solutionPfor any δc<δ ≤1.Meanwhile,for any initial conditionP0≥0,P=limk→∞Pkholds ifPksatisfies

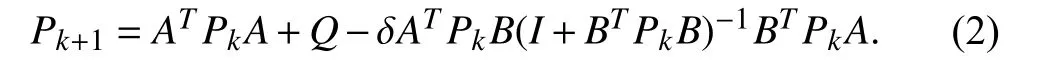
Remark 1:It is not hard to see that the Riccati equation (1)is reduced to a Lyapunov equation if δ=0.If δ=1,the equation (1) is degenerated to the common discrete-time Riccati equation.

Lemma 4 [47]:For the Laplacian matrix L,the followingN×Nnonsingular matrixUcan be found

whereU1∈RN×(N−1),U2∈R(N−1)×Nand υT1N=1,υTL=0,such that

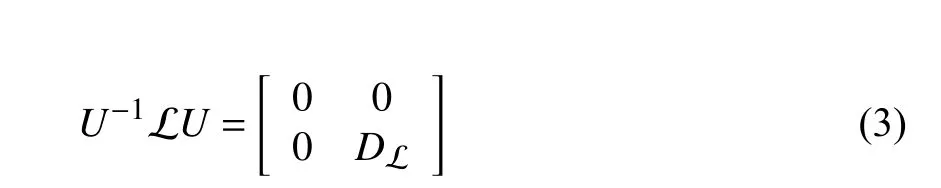
whereDLis an upper-triangular matrix,and the diagonal elements λiof which satisfies R e(λi)>0,i=2,3,...,N.

Consider a leader-following multi-agent system consisting of one leader andNfollowers.Let G′be a directed graph with theseN+1 nodes.G′is used to model the communicating topology of the multi-agent system,and G′containsν0(denoting the leader) and a subgraph G.It is supposed in this work that at least one following agent of G is connected to the leader ν0via a direct edge,and graph G′contains a directed spanning tree rooted at the leader.

In discussing time-varying interaction topology,the set of graph{s for the exi}sting interaction topologies is given aswith index set P={1,2,...,m}.Let σ:[0,∞)→Pbe a switching signal used to describe the topology switching between subintervals.Lσdenotes the Laplacian of graphwith switching signal σ.The dynamics of the following agents are described by the following discrete-time linear systems

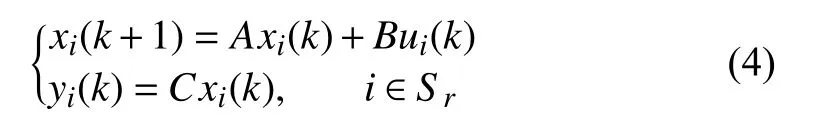
wherexi∈Rn,ui∈Rpandyi∈Rqare the state,control input and measured output of agenti,respectively.A∈Rn×n,B∈Rn×pandC∈Rq×nare constant matrices.Based on the above dynamics equation and supposingCis full row rank,it would not be difficult to select a matrixT∈R(n−q)×nsuch thatis non-singular.

The leader’s dynamics is described by

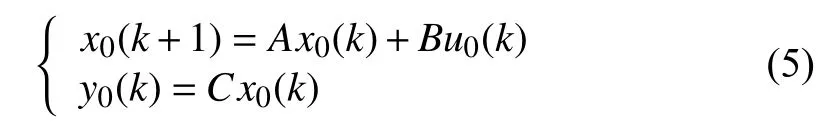
wherex0∈Rnis the leader’s state,y0∈Rqis the output of leader andu0∈Rpis the input of leader.

Remark 2:It is assumed in this work thatu0(k) is known by all followers,here we consider the case that the leader’s control input is nonzero.The coefficient matrices for the leader are supposed to be the same as those of the followers due to practical backgrounds including birds,insects,etc.

Assumption 1:Each directed communi cation topologyG′has a directed spanning tree.

Assumption 2:The matrix pair (A,B) is stabilizable,(A,C) is detectable.Cis a full row rank matrix,namelyrank(C)=q.

Assumption 3:The followers can only receive the relative output measurements with their neighbors directly.

The leader-following system (4) and (5) is said to achieve consensus,if

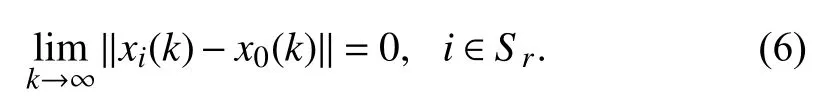
The purpose of this paper is to design a distributed reducedorder observer-based control protocolui(k) using only the relative output feedback information for formation control problems of a leader-following discrete-time linear system.Specifying a formation by a vectorin whichhi∈Rnis the desired relative place of agentito the leader,then the leader-following system is said to achieve formationhif

III.MAIN RESULTS

A.Generalized Reduced-Order Observer

In this subsection,a distributed reduced-order observer is introduced for each following agent in (4):

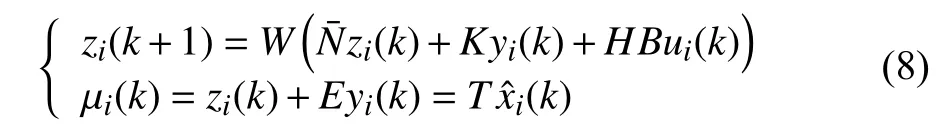
Remark 3:For consensus control of linear multi-agent systems,the distributed continuous-time reduced observers were designed in [33] and [34].Motivated by the works [33]and [34],a novel distributed discrete-time reduced-order observer is designed based on the relative output information.Based on the Lyapunov method and the modified discretetime algebraic Riccati equation,a multi-step control algorithm is established for leader-following formation control of discrete-time linear multi-agent systems.

Theorem 1:Consider a general discrete-time system model(4),and suppose that Assumptions 1–3 hold.If the following conditions (10) of coefficient matrices hold,andis Schur stable,the estimation errorei(k) converge to zero exponentially asymptotically,which means that the observer(8) can estimate the state ofTxieffectively.

B.Discrete-Time Formation Control of Linear Systems

In this subsection,a distributed control protocol is proposed,utilizing merely the relative output feedback information for leader-following formation control.Considering the formation definition (7),a new state vector can be designed as follow:

Theorem 2:Consider the leader-following systems (4) and(5) with the control protocol (21) and the reduced-order observer (20),and suppose that Assumptions 1–3 hold.Then,the considered system can achieve formation control if condition (22) holds.The gain matrixMis chosen asand the constantc,matricesP1,Eare obtained via Algorithm 1.

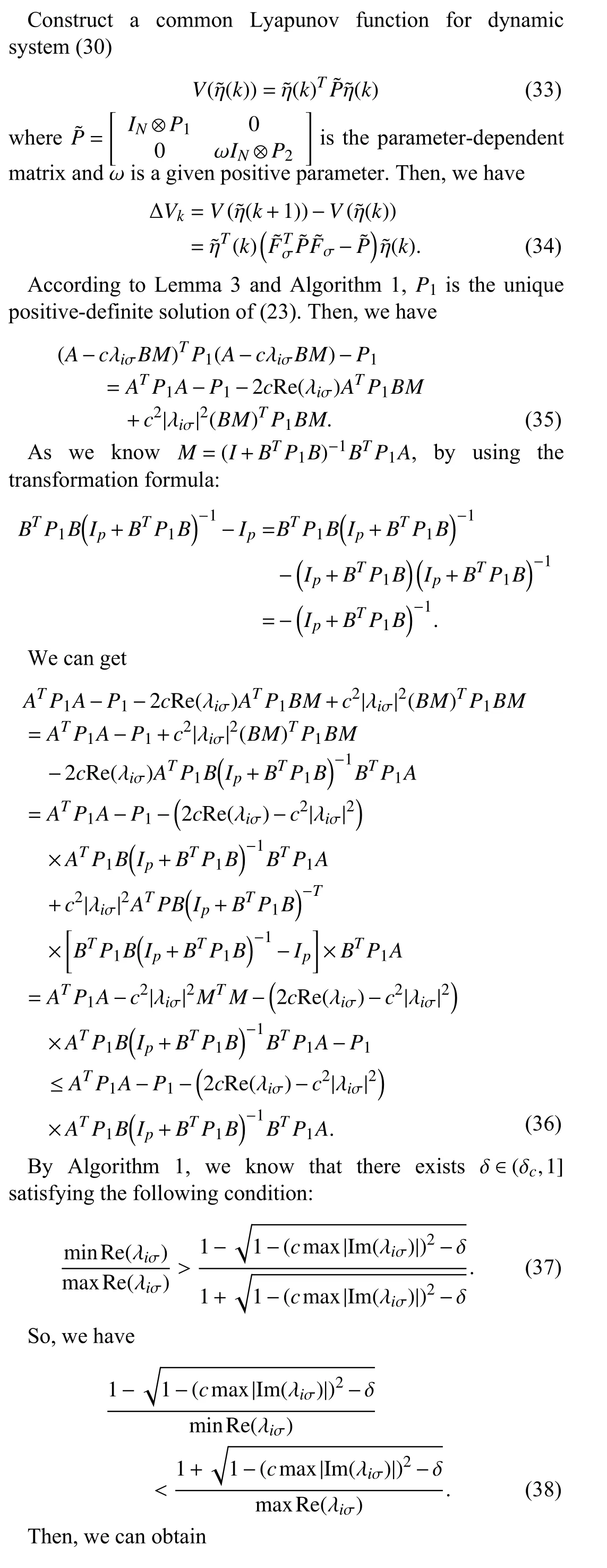
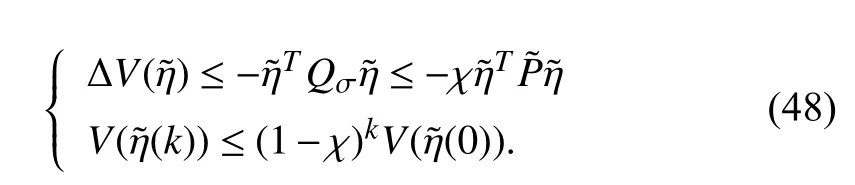
Thus,the system (30) is exponentially asymptotically stable,the formation problem is solved by the control protocol (21)and the reduced-order observer (20),i.e.,x0(k)−hi‖=0 ∀i∈Sr.■

Remark 5:It can be seen that if we choose the formation vectorh=0,the consensus problem of multi-agent system (4)and (5) can be solved if (7) holds.Thus,the consensus problem is a special case of the formation problem.The observer-based consensus problem of discrete-time linear systems has been studied in [10].The common Lyapunov function is available for all interaction topologies,and under certain conditions the switching topology can be extended to the jointly connected topology case that each of the subsystems is unstable.

Remark 6:Compared with most of current works on consensus control with undirected switching topology,leaderfollowing formation control for discrete-time linear multiagent systems with directed switching topology is first considered in this work.Under directed topology,the Laplacian matrix associated with the communication graph is asymmetrical.The eigenvalues of the matrix have an imaginary part because the Laplacian matrix associated with communication topology is asymmetric.Comparing the controller and observer design with undirected switching topology then becomes difficult.Moreover,using switching communication,the description and certification of theoretical results becomes complicated and difficult for a system with directed topology.

IV.SIMULATIONS

A numerical simulation is provided in this section to illustrate the effectiveness of the theoretical results.Consider a group of agents consisting of four followers and one leader.Fig.1 shows the switching communication topology.The coefficient matrices of both leader and follower dynamics are given as

Fig.1.Switching communication topology graph.

The topologies are arbitrarily switched among the three graphs

The observer coefficient matrixT=[0,0,1]T,and some coefficient matrices of control protocol (21) are given as follows:

Through simple calculations,we can getThen,take δ=0.4 andc=0.3 which satisfies the above conditions.We can obtain

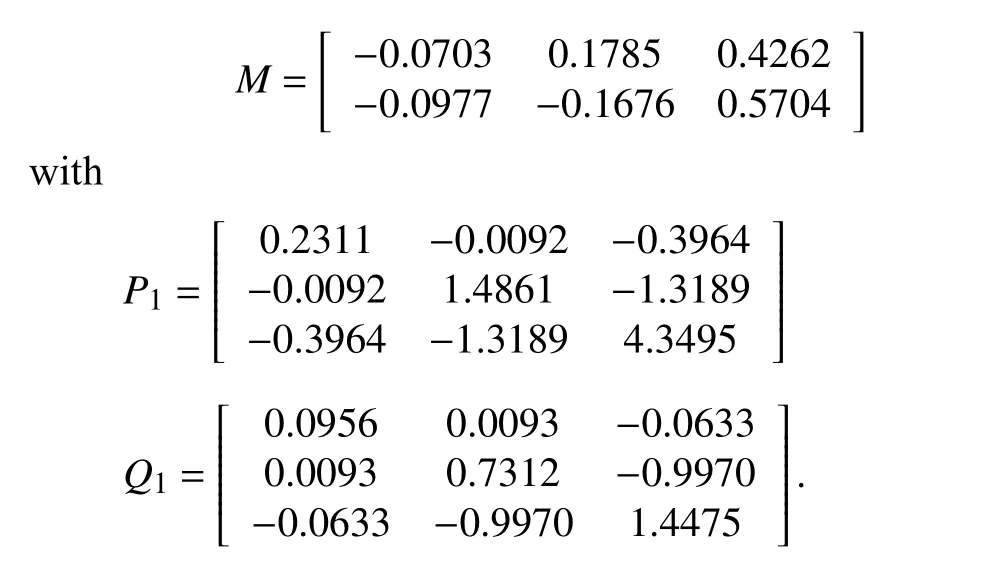
In general,x0(0) is taken as [10,−5,15]Tandu0(k) is taken as [2,1]T.The initial states of the following agents are random generated with an item in each dimension in the interval[−30,30].Choosing a simple formation vectorh=[[2,−2,−2]T,[−2,2,2]T,[4,3,2]T,[−4,−3,−2]T]Tfor the leader-following system.Figs.2–3 shows the estimation errorei(k)and the state ψi1(k) of four followers.The position trajectories of leaders and followers under the protocol (21)are showed in Figs.4–7.It is shown that the multi-agent system can achieve the expected formation.Now,the feasibility and effectiveness of protocols (20) and (21) are now verified.

Fig.2.Estimation error trajectories of four followers.

Fig.3.State trajectories of the observers.

V.CONCLUSIONS

In this work,a novel reduced-order observer-based control law is presented for leader-following formation of discretetime linear multi-agent systems with directed switching topologies by utilizing the relative output information of neighboring agents.Using the model transformation method,the formation control problem is converted into an output feedback control problem with a reduced-order observer of the associated switching system.Based on the Lyapunov method and the modified discrete-time algebraic Riccati equation,a sufficient condition is obtained to ensure that the discrete-time linear multi-agent system can achieve the expected leaderfollowing formation.Future works will focus on parameter time-changing systems.

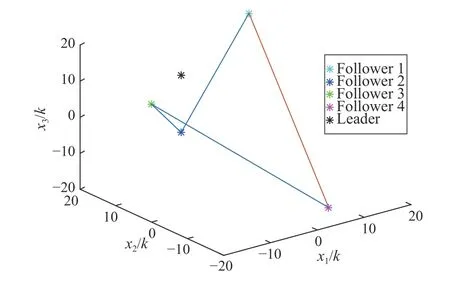
Fig.4.Position trajectories:k=0.

Fig.5.Position trajectories:k=15.

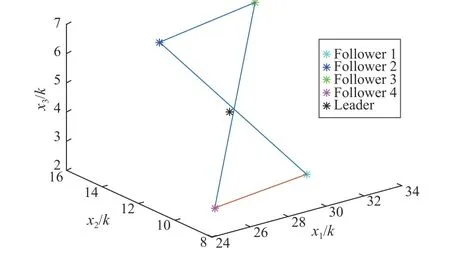
Fig.6.Position trajectories:k=30.

Fig.7.Position trajectories:k=45.