Distributed Order-Up-To Inventory Control in Networked Supply Systems With Delay

Przemysław Ignaciuk,

Abstract—In this work,the dynamics of networked goods distribution systems subject to the control of a continuous-review order-up-to inventory policy are investigated.In the analytical study,as opposed to the earlier models constrained to the serial and arborescent interconnection structures,an arbitrary multiechelon topology is considered.This external,uncertain demand,following any distribution,may be imposed on all network nodes,not just conveniently selected contact points.As in the physical systems,stock relocation to refill the reserves is subject to nonnegligible delay,which poses a severe stability threat and may lead to cost-inefficient decisions.A state-space model is created and used as the framework for analyzing system properties.In particular,it is formally demonstrated that despite unpredictable demand fluctuations,a feasible (nonnegative and bounded)reserves replenishment signal is generated at all times,and the stock gathered at the nodes does not surpass a finite,precisely determined level.The theoretical content is illustrated with a case study of the Chinese oil supply system.

I.INTRODUCTION

THE challenges associated with complex connectivity architectures in current production and goods distribution systems predispose control policy selection towards numerical methods [1]–[3] and approximate solutions [4],[5].Formal studies are primarily restricted to basic configurations:singleechelon [6],serial [7],or arborescent (with separable paths of goods flow) [8]–[10].In contrast,this work aims to establish a formal framework to analyze the dynamics of modern distribution systems organize in a more complex– networked– scheme of suppliers,distribution centers,and retailers exchanging resources with a delay according to the popular order-up-to (OUT) inventory policy [11].

Earlier studies on distribution system dynamics regulated by the OUT policy are summarized in [12].Later on,using the transfer-function approach,Hoberget al.[13] assessed the impact of delay on the stability of the periodic-review twoechelon configuration.The study was extended over perishable inventories in [14] and variability containment objectives in [15].In [16],a block-diagram manipulation was employed to give more insights into the dynamical phenomena in contemporary supply chains,albeit still limited to the localized approximation.The serial configuration in a discrete-time framework was investigated in [17] as a basis forH∞-optimal controller design,and in [18] for modelpredictive control.A continuous-time model of a similar system was developed in [7] to help in choosing suitable gains for the modified– proportional OUT policy.The works on the arborescent retarded systems continued in [19]–[21],targeting parameter selection to improve stability margin [19],reduce variability [20],or costs [21],under a given demand type.

Approximating the presently deployed multi-echelon systems with non-trivial interconnection dependencies [22],[23] by fundamental constructs leads to cost increase,or even instability [24],[25].In this paper,as opposed to [6]–[10],[13]–[21],the networked nature of resource distribution systems is given explicit consideration.The constructed framework allows for an arbitrary interconnection topology among system elements (nodes) and uncertain,time-varying demand to be placed at any node.The excess demand is lost,which breaks the frequently applied simplification to linear stock dynamics [12],[15].The reserves,from which both the exogenous and internal demand is served,are acquired with non-zero lead-time delay.

The contributions of this paper include providing a statespace model of networked goods distribution systems with retarded transshipments and lost sales and conducting an analytical study of OUT policy dynamical performance.It is formally shown that the policy always issues a feasible,i.e.,nonnegative and bounded,replenishment signal despite having no knowledge of demand future evolution,or a global perspective on the system interconnection structure.The stock level at the nodes is demonstrated to be nonnegative and upper-bounded.The policy can thus be safely deployed in current systems with cross-border cooperation,in a fully distributed mode.The choice of the reference stock level for high demand satisfaction rate is indicated.The inventory managers are thus equipped with explicit guidelines regarding the selection of storage space at the nodes and maximizing the response towards external actors.Consequently,the attractive image of a reliable goods provider is established,and solid,long-term business relationships may be formed.The theoretical content is illustrated via a case study of the Chinese oil supply system [9].

II.ANALYTICAL FRAMEWORk

In the considered class of systems,suppliers,distribution centers,and retailers interact with each other in goods exchange so that an exogenous,uncertain demand is satisfied.The controlled elements– distribution centers,retailers– will be termed“nodes.”An example setting comprising six nodes,three of which are subjected to market demand,and two external suppliers is sketched in Fig.1.Neither the statistical parameters nor the actual demand pattern is accessible beforehand.From a logistic system perspective,the demand constitutes a driving factor for ordering decisions to refill stock.Hence,there are two types of inputs:the exogenous signal– demand– that in the dynamical framework is treated as a perturbation,and the control signal– the sequence of stock refill decisions.

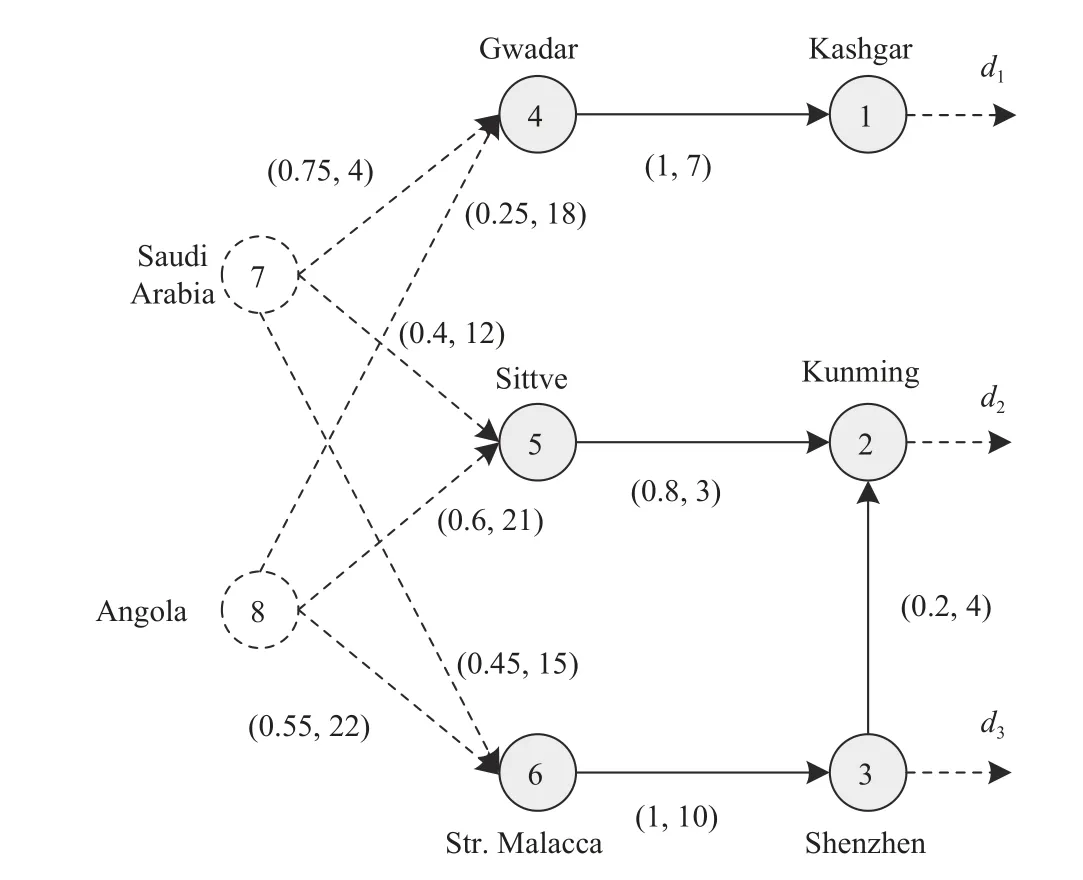
Fig.1.Chinese oil supply system:1–6 controlled nodes,7,8 external sources.Demand is placed at nodes 1–3.The numbers at the links signify:(supplier contribution,delivery delay).

As opposed to [6]–[10],[13]–[21],an arbitrary system topology in which a unidirectional path connecting each controlled node with at least one supplier exists is considered.In the proposed model,the topology encompassesnnodes whose indices are taken from the setXn={1,2,…,n}.The stock gathered at the nodes,used to answer the demand,is refilled frommexternal suppliers.The set of indices of all nodes and suppliers isX={1,2,…,m+n}.

The evolution of time will be tracked by the continuous variablet.Letxi(t) denote the stock level at nodei,i∈Xn,at instantt,anddi(t) be the intensity of external demand placed at that node.The operations performed at the node proceed according to the following sequence:

1) Determine the current stock levelxi(t),received shipmentsand external demanddi(t).

2) Fulfill the demand up to the volume of available resources.In the case of a deficit,the surplus demand is realized elsewhere– a lost-sales system.

3) Record the (internal) replenishment requests from neighbors in the network.

4) Respond to internal requests using leftover resources.In the case of deficit,the requested quantity is proportionally reduced,i.e.,the shortage at timetat nodei,sayεi(t),implies the reduction of the lot sent towards nodej,uj(t),touj(t)[1–– the set of node indices for which nodeisupplies goods.

The reserves gathered at a node are used to fulfill both external market demand and internal requests from the neighbors,with external demand given priority to achieve a better company image.Unlike previous similar approaches to the analysis of inventory system dynamics,e.g.,[9],in the presented model,the demand may be placed at any node.Although substantially complicates the design framework,this premise allows one to relate to the phenomena occurring in the currently deployed physical systems more closely.

The demand is represented by an a priori unknown,timevarying function

The request issued by nodeiat timetfor its suppliers(external sources and neighbors in the system) will be denoted byui(t),i∈Xn,and the lot to be retrieved from supplierj,j∈X,via partitioning coefficientφji(t) ∈ [0,1].Consequently,the quantity of the goods sent by nodeito the neighbors

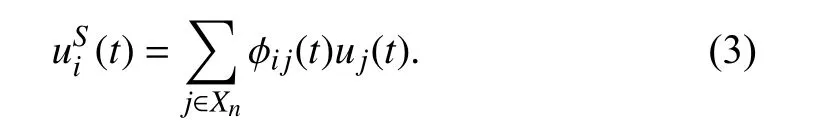
If the nominal order partitioning:is not possible because of a goods shortage,the coefficients are reduced as dictated by rule 4.More specifically,if nodejhas gathered enough resources to respond to the request from node i immediately,thenotherwiseand

The external suppliers are assumed to be uncapacitated(they do not experience shortage).Coefficientsφijreflect the connection structure.Without losing generality,it is assumed that no node is isolated,i.e.,a path exists from each node to at least one external source,and the network is directed,i.e.,φji(t) ≠ 0 impliesφij(t)=0,andφii(t)=0,to preclude selfsupply.

The order realization takes a non-negligible amount of time.The delay in goods provision from nodejtoiwill be denoted byhji,hji∈H,H– the set of all delay values at the internode links.With this notation,the quantity of the goods received by nodeiat instanttis

In order to perform a detailed,formalanalysis,a state-space description of the system dynamics will be introduced.The following representation is proposed

where,

1)x(t)=[x1(t) ···xn(t)]Tis the state vector (stock level at the nodes),

2)u(t)=[u1(t) ···un(t)]Tis the controlled input (replenishment quantity requested by the nodes),

3)s(t)=[s1(t) ···sn(t)]Tis the perturbing input which expresses the uncertainty in demand realization at the nodes;withone has from (1)

For the sake of further analysis,a matrix,grouping the topological information,will be defined as

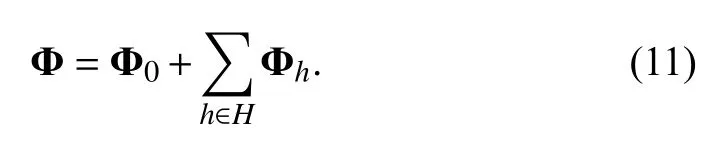
The time reference has been dropped in (11) to emphasize the nominal– no-goods-shortage– conditions.

Lemma 1:Matrix Φ given by (11) has a positive inverse.

Proof:One needs to show that all the entries of Φ–1are nonnegative.In the nominal case,for eachi,one has from (4),

III.ORDER-UP-TO INVENTORY CONTROL

The OUT policy states that the stock should be refilled to a reference level whenever it falls below this level.In systems with non-negligible delivery delays,the quantity of the goods in transit needs to be incorporated into the replenishment request,usually through the inventory position [11,ch.3].

The order quantity at nodeiat instanttis determined as(forecasts ignored)

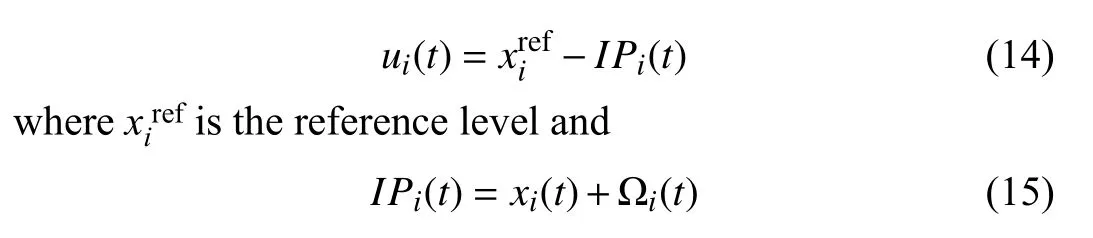
is the inventory position,which holds information about the on-hand stockxi(t) and the transported goods Ωi(t),i.e.,the shipments already requested but not yet procured due to delays.The open-order quantity Ωi(t) is calculated by tracking the difference between the requested and retrieved resources as

For notational convenience,the summation in (17) is taken over allj∈X.However,coefficientsφji(·) are non-zero only for the nodeisuppliers.

Looking at (17) from the perspective of a control system,the calculation of the replenishment quantity– the input signal–proceeds according to proportional control (with unity gain)with dead-time compensation.Since resource accumulation at the nodes is an integrating process,the controlled plant is an integrator.In turn,tracking the open-order quantity may be interpreted as an operation of the Smith predictor.The presence of multiple channels in the network,however,requires extending the classical predictor structure over multiple loops modulated by time-varying weighting coefficients.The block diagram of control structure (17) is illustrated in Fig.2.The weightsφji(t) change with time with respect to the resource state at the upstream nodes.If the delay undergoes uncertain variations,to uphold the information about the open-order quantity,the delay compensator may be complemented by a corrective term,as in [26].The continuous-time systems,however,require separate treatment,possibly using recent advancements [27],[28].

Fig.2.OUT policy in a time-delay system perspective.

In order to establish a replenishment order,the OUT policy needs no explicit information from other nodes– it can be conveniently deployed in a distributed fashion.However,the ordering decisions will impact the entire system state owing to a non-trivial interconnection topology.To examine the control system properties as a whole,a state-space policy representation,consistent with (6),will be introduced.

First,the information about reference levels is grouped into the vectorWith this notation,using(6)–(9),the OUT policy (17),implemented independently at the nodes,can be synthesized into a vector form as

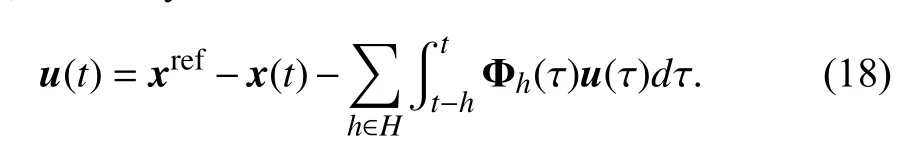
IV.OUT POLICY PROPERTY ANALYSIS

It follows from (18) thatu(0)=xref–x(0).Consequently,for a feasible (nonnegative and upper-bounded) replenishment signal,one needs to choose the reference asxref≥x(0).The theorem below demonstrates thaturemains feasible for anyt>0 despite a priori unknown demand fluctuations.

Theorem 2:The input signalu(t) in system (6),generated according to (18),is nonnegative and upper-bounded for anyt>0.

The control process commences withu(0)=xref–x(0) ≥ 0.Hence,it follows from (20) and (21) that the components ofudecrease as long as they are bigger than the corresponding components of vector s,which are nonnegative by definition.Consequently,they may not drop below zero.In turn,to establish the maximum value of the replenishment signal,it is necessary to investigate the case whenIn those circumstances,onceui(·) reaches the corresponding level of vector(constraint (7)),uimay never grow beyond that level again,andu(t) ≤ Φ–1dmax.■

The derivations presented so far prove that to ensure a realizable– non-negative– stock replenishment signal,the reference level cannot be set lower than the initial reserves.Equivalently,only such set of the initial states is permitted,which conform to the inequalityx(0) ≤xref.The theorem formulated in a later part of the text demonstrates that the stock never grows beyond the reference level,which thus designates the storage space to be reserved at the nodes.

Theorem 3:If control (18) is applied in system (6) to regulate the goods distribution process,then the stock accumulated at the nodes is nonnegative and does not exceed the reference level,i.e.,

Proof:Rules 2 and 4 implyxi(t) ≥ 0 at any node.Consequently,x(t) ≥ 0,and it remains to show that for anyt≥0 the upper bound dictated by (22) is also satisfied.

The reference stock level is chosen so thatx(0) ≤xref.Applying (19) to (6),yields

By definition,Φh≥ 0 and s(t) ≥ 0.In turn,it follows from Lemma 1 that the inverse of Φ is a positive matrix (it contains only nonnegative entries).Hence,using (25),x(t) ≤xref.■

Theorem 3 shows that the warehouse space equal to the stock reference level is sufficient to store all goods transported to each node.Thus (costly) emergency storage is never required.Another desirable property is being able to obtain a high service level,i.e.,to satisfy as much of the demand as possible from the immediately available resources.The sequel demonstrates how to achieve full demand satisfaction by selecting a single design parameter– the stock reference level.

V.NUMERICAL ExAMPLE

The characteristics of the resource distribution process will be illustrated for the example setting depicted in Fig.1,which reflects the China oil supply system [9].The oil for market contact points 1–3,responding to demandsd1–d3,is delivered through intermediate nodes 4–6 using channels with different parameters (φij– lot partitioning,hij– delay),originating at two external sources 7 and 8.The demand,depicted in Fig.3,experiences seasonal variations with abrupt,unanticipated intensity shifts.The stock replenishment in the controlled network (nodes 1–6) is regulated by the OUT policy (18).AssumingMbpd (millions of barrels per day),the reference level is selected according to(27) asxref=[20.5 15 63 21.5 52 113.5]TMb to maximize the service rate.The initial conditionx(0)=xref.

The analytical findings from Section IV regarding the OUT policy performance are verified in relation to another common policy– (r,Q) one– that states that one must refill the stock byQunits when the level of reserves drops belowr,which is useful when the trading agreements favor shipments of a predetermined quantity.Here,Qis set equal to the large crude oil tanker capacity of 2.0 Mb.The stock evolution under the OUT policy is sketched in Fig.4 and under the (r,Q) one in Fig.5.One can learn from Fig.4 that,precisely as dictated by Theorem 3,the OUT policy keeps the stock within the allocated storage space set asxref.The stock stays positive even when the demand is at its maximum,which means a full service rate and uninterrupted oil supply despite a priori unknown demand changes.Although the (r,Q) policy generates smaller holding costs at intermediate nodes 4–6,it leads to unfulfilled demand at the end-points.As evidenced in Fig.5,the reserves drop to zero in response to a demand surge(at node 2:days 18–25,at node 3:days 33–40),which implies inconsistent supplies.

Fig.3.Daily demand.

Fig.4.Stock level evolution under OUT policy.

Fig.5.Stock level evolution under (r,Q) policy.

VI.SUMMARY AND CONCLUSIONS

In the paper,a framework to conduct a formal analysis of inventory policy dynamics in systems with complex,networked structures has been provided.It was proved that irrespective of the demand pattern imposed onto the system,the OUT policy generates a nonnegative and upper-bounded stock replenishment signal,even though it has access to local information only.It was also shown that the stock of goods accumulating at the nodes does not grow beyond the reference level.Thus,it was formally demonstrated that this popularamong-practitioners strategy could be safely deployed in modern,multi-dimensional distribution systems.Moreover,guidelines for tuning policy performance to maximize the service level have been provided.As a result,the image towards external actors of a reliable goods distributor can be preserved,even in the uncertain lost-sales setting.While the analytical study emphasizes the OUT policy,the framework is flexible to investigate the performance of other inventory control strategies,e.g.,a nonlinear (r,Q) policy.It is a subject of the current work to be reported in future publications.