利用视加速度补偿和推力逐级释放的垂直着陆制导方法*

周 鼎，陈韦贤，邱 伟

(上海宇航系统工程研究所·上海·201109)

0 引 言

着陆段是运载火箭子级垂直返回的最后阶段，也是回收过程中技术难度较大的部分。子级在动力学特性和飞行环境高动态变化、强扰动和大参数不确定的情况下，需要以有限的控制能力实现大范围减速，并且满足复杂的位姿状态约束及狭窄的终端硬约束，这对制导和控制提出了很高的要求。经典的离线标称轨迹设计结合跟踪制导律的方法呈现出在适应性方面的不足，而广泛应用于月面和行星着陆的多项式制导又无法处理推力大小及与方向相关的约束，因此，利用当前更新的飞行状态开展在线轨迹规划进而实施跟踪制导的方法已成为现在的研究重点之一。

随着硬件平台计算能力的不断提升，利用迭代优化的计算制导已成为近年来有希望突破瓶颈的技术途径，其中快速发展的研究热点是基于凸优化的在线轨迹规划方法。加州理工大学JPL实验室和Acikmese教授团队基于火星动力学下降任务在凸优化理论推广及工程化方面取得了无损凸化、定制化内点法、G-FOLD制导算法飞行试验、时间最优连续凸化等一系列重要成果。与火星着陆不同，运载火箭子级在地球上的返回过程中，受大气环境的影响比较显著，气动力虽然相对于推力(控制力)而言并非“主导力”，但其存在较大的模型偏差及不确定性，这要求制导方法对气动力系数偏差具备较强的鲁棒性。现有研究的主要关注点多集中于如何改善轨迹优化性能，针对获得优化轨迹后如何形成较好的闭环制导的相关研究还比较少。因此在轨迹在线规划的基础上，子级还需要具备足够的控制能力来补偿气动力的偏差。在这样的需求牵引下，本文通过在线滚动规划进行子级着陆的闭环制导，并提出了视加速度补偿和推力逐级释放的两种策略对制导方法进行调整。

1 着陆段在线轨迹规划

本节给出了着陆段在线轨迹规划涉及的问题模型、规划算法及定制化求解器。

1.1 轨迹优化问题描述

依据参考文献[3]中的坐标系定义，在着陆点坐标系下建立运载火箭子级着陆段的动力学模型。在建模时仅考虑气动阻力，依靠发动机进行制动和控制；此外，考虑着陆段的飞行距离较短，在这一过程中可将引力场近似为平行引力场。相应的轨迹优化问题(问题1)可描述为：

(1)目标函数

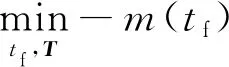
(1)

其中，

m

为子级质量，

t

为终端时间，为发动机推力矢量；此处选取剩余质量最大为指标是为了使着陆过程的推进剂消耗最小化，从发射主任务的角度看这种方式可以将更多的运载能力用于提升载荷质量。

(2)动力学约束

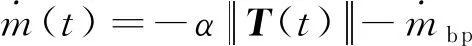
(2)

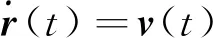
(3)

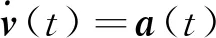
(4)

(5)

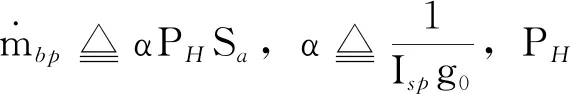
(3)状态约束

m

≤

m

(

t

)

(6)

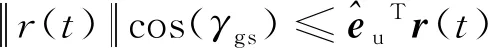
(7)

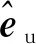
(4)控制约束

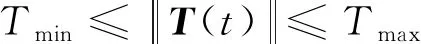
(8)

(9)

(5)边值条件

(10)

(11)

1.2 问题离散与凸化

上述着陆段轨迹优化的问题1是一个非线性、非凸的连续最优控制问题，在利用凸优化方法进行求解前，需要对问题进行离散化和凸化处理。本文采用一阶保持离散，并对推力进行无损凸化处理。动力学相关离散公式参见文献[13]。这里给出控制约束的离散凸化

(12)

T

≤

Γ

[

k

]≤

T

(13)

(14)

其中，

N

为离散节点数，

Γ

为推力松弛变量。

1.3 序列迭代

此时的动力学中仍然存在非凸的气动阻力项[

k

]，考虑采用序列线性化进行迭代凸化近似。为保证连续两次迭代之间的状态量满足线性化的小偏量假设，引入信赖域变量进行约束，即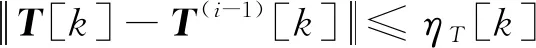

(15)

|Δ

t

-Δ

t

(-1)|≤

η

Δ

(16)

其中，

k

∈[0,

N

-1]，

η

为推力信赖域，Δ

t

为离散区间时长，

η

Δ为相应的信赖域，上角标(

i

-1)表示前一次迭代的解，

i

=1,2,…。

此外，为减缓人为线性化带来的问题不可行风险，引入松弛加速度变量作为虚拟控制，相关约束如下

(17)

其中，为松弛加速度，

κ

R为相应的边界。

在序列迭代的过程中主要涉及两个问题模型：初始参考轨迹生成模型和迭代求解模型。

(1)初始参考轨迹生成

该模型用于生成初始参考轨迹以启动算法，需要给出初始参考质量和速度大小的序列

μ

[

k

]和

s

[

k

]，相应的阻力和加速度可以离散凸化表示为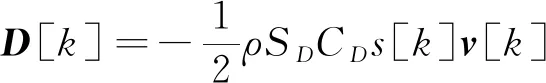

(18)

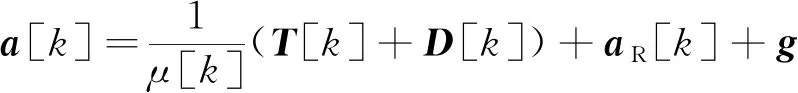
(19)

初始参考轨迹优化记为问题2-I，其目标函数为

(20)

其中，R=[

κ

R[0],

κ

R[1],…,

κ

R[

N

-1]]，

ω

R为虚拟控制罚因子。

(2)迭代求解

序列迭代问题(问题2-II)与初始化问题(问题2-I)相比增加了信赖域变量及离散时间变量，含非凸气动阻力的加速度等式约束采用如下离散凸化形式

[

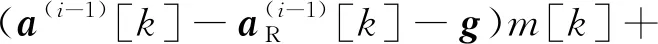
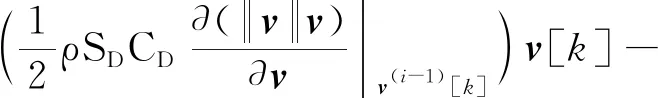
k

]+

m

(-1)[

k

][

k

]-

m

(-1)[

k

][

k

]

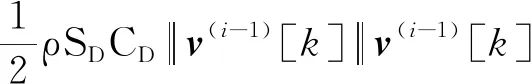
(21)

相应地，问题(问题2-II)的目标函数为

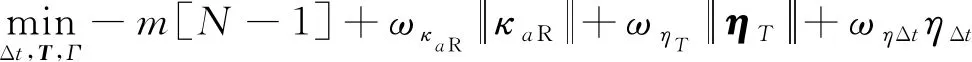
(22)

其中，=[

η

[0],

η

[1],…,

η

[

N

-1]]，

ω

和

ω

Δ为信赖域罚因子。

1.4 定制化内点法求解器

无论是初始参考轨迹生成(问题2-I)还是迭代求解(问题2-II)，相应的凸化问题都可以表示为标准的二阶锥规划(Second-Order Cone Programming，SOCP)问题，即

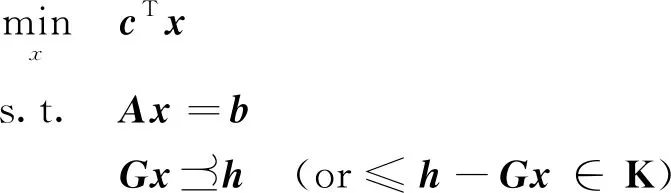
(23)

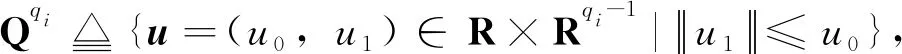
考虑在线规划的任务需求，本节针对上述SOCP问题定制求解器，给出求解所用的原-对偶路径跟随内点算法的实现流程如下。内点算法相关理论细节参见文献[11]。其中，SOCP问题的最优性条件称为KKT(Karush-Kuhn-Tucker)条件，相应的KKT矩阵为

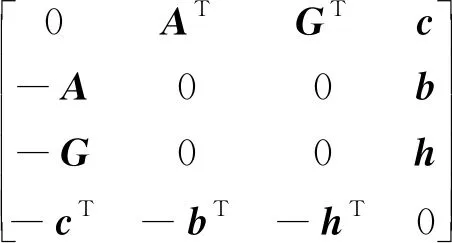
图1 二阶锥规划问题求解定制化内点算法流程Fig.1 Customized interior point method flowchart for solving second-order cone programming

2 着陆段制导律设计

2.1 基于滚动时域在线规划的闭环制导

本节基于滚动时域控制的思想，利用SOCP问题在线求解的快速性和良好的收敛性，设计子级着陆段的闭环制导算法。算法以较高频的频率利用当前的导航信息构建轨迹优化问题，并通过序列凸化进行迭代求解，将优化解以前馈指令的形式作用于火箭子级；同时，考虑模型偏差和不确定性，对推力进行逐级调整和视加速度补偿。

2.2 推力逐级释放

采用上述滚动时域的闭环制导策略，整个着陆过程中需要进行多次在线轨迹规划。在着陆段前期给出的指令一般为最小推力，经过一定的制导更新周期后，指令均为最大推力，这符合燃料最省动力下降的Bang-Bang控制规律；然而，在干扰及偏差存在的情况下，前期采取的小推力可能会增大后期的控制负担，导致即使在后期施加最大推力也难以实现着陆要求的终端控制精度。为此，本文提出了一种逐级释放推力能力的策略。

对整个着陆段进行分段，每个子阶段的最大推力是固定的，但随着飞行时间增加，最大推力逐级增大，最后一段的最大推力与子级实际可允许的最大推力相等。在前期制导中，由于最大推力减小，调节范围变小，使得产生的推力指令倾向于采用最大控制能力，避免前期生成的指令过于保守；后期制导系统可用的控制能力余量也足够，而最大推力也按照分段逐级增大，保证了后期具有足够的控制能力。图2给出了一种推力逐级释放的示例。

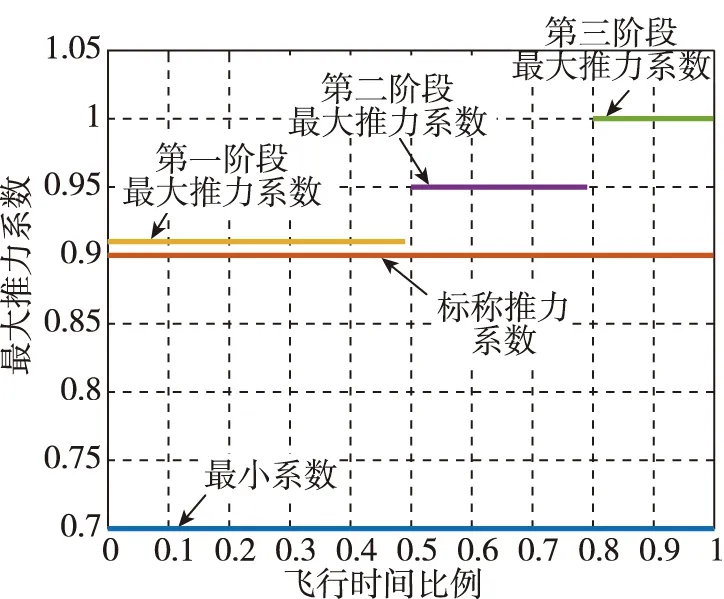
图2 推力逐级释放示意图Fig.2 Illustration for thrust level-wise release

子阶段划分的原则为：在着陆段前期飞行中，由干扰引起的误差是一个逐步积累的过程，即使前期制导精度很高，仍会有部分误差传递至后期飞行中，所以前期飞行精度对整个着陆段终端精度的影响不大，故可将飞行前期阶段单独处理。当飞行到中间靠后阶段时，此时的误差便能直接影响终端着陆精度，因此这个阶段的制导精度保持在一个较高水平。当能力不足时,必须逐级调整最大推力系数，直到制导方法的能力能够应对消除状态误差。当火箭接近着陆点时，其状态误差对着陆点精度的影响最大，需要完全放开火箭的控制能力，利用制导系统保证着陆点精度达到要求。如图2所示，在推力逐级释放策略中，每一段的最大推力系数是根据算法及闭环仿真中的调试测试经验确定的，一般可按约5%的推力逐级进行调节。

2.3 视加速度补偿

在每个制导更新周期内，为保证干扰及偏差下的飞行精度，需要跟踪在线生成的轨迹。本文考虑将可以直接测量的视加速度作为特征量进行轨迹跟踪。具体步骤如下：

(1)计算当前周期视加速度预测值

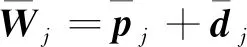
(24)

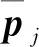
(2)计算补偿后的视加速度

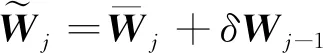
(25)

(3)获取当前周期实测的视加速度

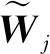
(4)计算下一周期的视加速度补偿量

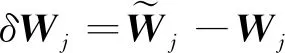
(26)

3 算例仿真与对比分析

本节以某运载火箭子级垂直着陆任务为背景，针对提出的制导算法及补偿策略进行了算例仿真与对比分析。

3.1 推力逐级释放效果

考虑初始质量、大气密度及气动阻力偏差，分别按无推力逐级释放和有推力逐级释放给出着陆段在线滚动规划在每个制导周期(周期为2s)内的规划成功/失败情况。其中，规划成功的标志是序列凸化迭代在有限的次数内收敛，本文设置的序列凸化迭代次数上界为10次。此外，根据仿真结果的统计分析，在主频为1.4GHz的环境下，在线规划所需的时间小于300ms，满足实时性需求。

在规划失败的情况下采用最近一次规划成功的结果进行推力插值，在制导周期内采用轨迹跟踪视加速度补偿。由表1可以看出，在第12个或13个制导周期后，规划均失败，说明此时子级的控制能力在物理上已无法满足着陆要求，这主要是由于前期规划过于保守而致使后期制导负担过大。

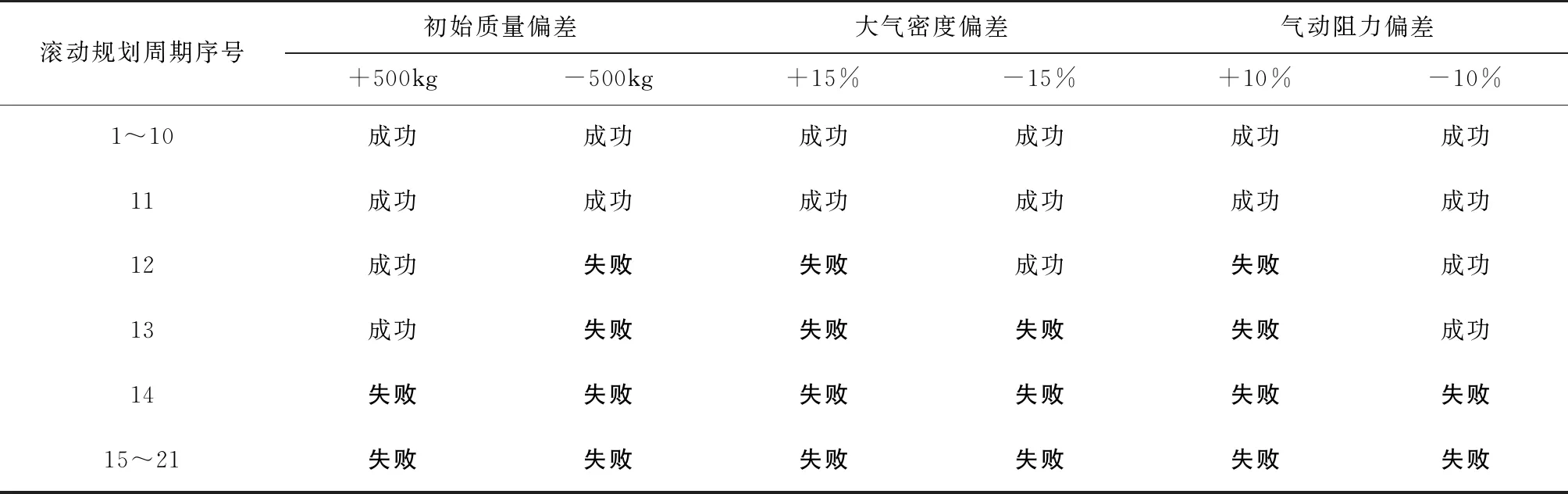
表1 无推力逐级释放的着陆段滚动规划情况Tab.1 Receding horizon planning for landing without thrust level-wise release

表2给出了引入推力逐级释放后的滚动规划情况。

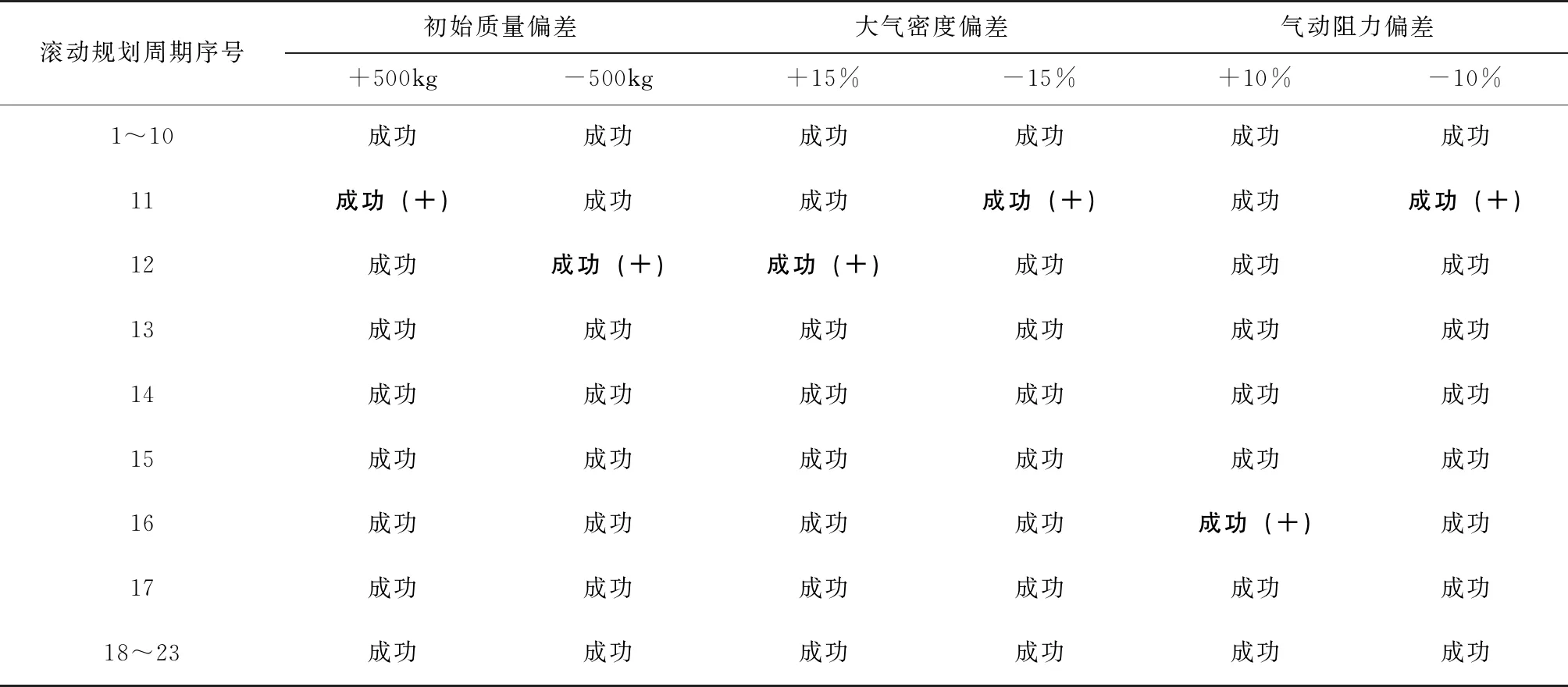
表2 考虑推力逐级释放的着陆段滚动规划情况Tab.2 Receding horizon planning for landing with thrust level-wise release

对比表1和表2可以看出，在引入推力逐级释放策略后，基本只需要进行一次推力上界的调整就可以使得滚动规划后续持续成功，表明该策略的加入对于提高在线规划成功率有比较好的效果，显著改善了制导的鲁棒性。

3.2 视加速度补偿效果

本节考虑着陆段初始质量偏差，对比分析视加速度补偿对滚动时域制导的影响。表3给出了相应的在线规划结果，在过程中加入了推力逐级释放策略。

表3 视加速度补偿对滚动规划的影响Tab.3 Effect of apparent acceleration compensation on receding horizon planning

可以看出，在未进行补偿的情况下，在第7个周期和第8个周期已经进行了推力释放的情况下，从第9个周期开始轨迹规划就出现了失败，递归可行性被破坏；而引入视加速度补偿后，滚动规划的递归可行性得以保持，且只在第11个周期进行了一次推力释放。结果表明，视加速度补偿可有效提高滚动规划的成功率。

4 结 论

本文以运载火箭子级垂直返回任务为背景，主要研究了着陆段滚动规划在线制导的补偿策略。考虑由于着陆段前期优化推力过于保守而致使后期制导负担增加的问题，提出了在制导过程中对推力上界进行逐级释放的策略；进一步考虑干扰和误差的影响，在滚动规划前馈指令基础上引入视加速度，对推力指令进行补偿以提升在线规划的成功率。最后，通过数值仿真及对比，验证了推力逐级释放和视加速度补偿策略对着陆段滚动规划在线制导鲁棒性的改善效果。

参考文献(

References

)

[1] 崔乃刚,吴荣,韦常柱,等.垂直起降可重复使用运载器发展现状与关键技术分析 [J].宇航总体技术,2018,2(2):27-42.

CUI N G,WU R,WEI C Z,et al.Development and key technologies of vertical takeoff vertical landing reusable launch vehicle[J].Astronautical Systems Engineering Technology,2018,2(2):27-42(in Chinese).

[2] 韦常柱,琚啸哲,徐大富,等.垂直起降重复使用运载器返回制导与控制 [J].航空学报,2019,40(7):322-345.

WEI C Z,JU X Z,XU D F,et al.Guidance and control for return process of vertical takeoff vertical landing reusable launching vehicle [J].Acta Aeronautica et Astronautica Sinica,2019,40(7):322-345(in Chinese).

[3] 王劲博.可重复使用运载火箭在线轨迹优化与制导方法研究 [D].哈尔滨:哈尔滨工业大学,2019.

WANG J B.Research on online trajectory optimization and guidance methods for reusable rocket[D].Harbin:Harbin Institute of Technology,2019(in Chinese).

[4] 吴荣.垂直起降可重复使用火箭返回制导与控制方法研究 [D].哈尔滨:哈尔滨工业大学,2019.

WU R.Research on guidance and control methods of vertical takeoff vertical landing reusable launch vehicle[D].Harbin:Harbin Institute of Technology,2019(in Chinese).

[5] 宋征宇,王聪.运载火箭返回着陆在线轨迹规划技术发展 [J].宇航总体技术,2019,3(6):1-12.

SONG Z Y,WANG C.Development of online trajectory planning technology for launch vehicle return and landing[J].Astronautical Systems Engineering Technology,2019,3(6):1-12(in Chinese).

[6] ACIKMESE B,PLOEN S.Convex programming approach to powered descent guidance for Mars landing [J].Journal of Guidance Control and Dynamics,2007,30(5):1353-1371.

[7] ACIKMESE B,BLACKMORE L,SCHARF D,et al.Enhancements on the convex programming based powered descent guidance algorithm for Mars landing[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit.2008:2008-6426.

[8] BLACKMORE L,ACIKMESE B,SCHARF D.Minimum-landing-error powered-descent guidance for Mars landing using convex optimization [J].Journal of Guidance Control and Dynamics,2010,33(4):1161-1175.

[9] ACIKMESE B,BLACKMORE L.Lossless convexification of a class of optimal control problems with non-convex control constraints [J].Automatica,2011,47(2):341-347.

[10] HARRIS M W,ACIKMESE B.Lossless convexification of non-convex optimal control problems for state constrained linear systems [J].Automatica,2014,50(9):2304-2311.

[11] DUERI D,ACIKMESE B,SCHARF D,et al.Customized real-time interior-point methods for onboard powered-descent guidance [J].Journal of Guidance,Control,and Dyna-mics,2016,40(2):197-212.

[12] SCHARF D P,ACIKMESE B,DUERI D,et al.Implementation and experimental demonstration of onboard powered-descent guidance [J].Journal of Guidance,Control,and Dynamics,2016,40(2):213-229.

[13] SZMUK M,ACIKMESE B.Successive convexification for 6-DoF Mars rocket powered descent landing with free-final-time[C]//AIAA,Guidance,Navigation,and Control Conference.2018:617-630.

[14] MALYUTA D,REYNOLDS T P,SZMUK M,et al.Discretization performance and accuracy analysis for the powered descent guidance problem [C]//AIAA SciTech Forum.2019:925-944.