你追我赶都是圆 一近一远交替现—浅谈核心素养下物理模型的构建

高仔芝 孙瑞华

《普通高中物理课程标准》（2017年版2020年修订）要求：“高中物理课程应在义务教育的基础上，进一步促进学生物理学科核心素养的养成和发展。”高中物理学科核心素养包括：物理观念、科学思维、实验探究、科学态度与责任，其中科学思维又将模型构建列为首个要素。因此，在一轮复习过程中我们必须关注模型的构建、拓展和延伸，提升学生能力，以期达到灵活运用的目的。

国家主席习近平在致第32届国际航空科学大会的贺信中指出：“航空科技是20世纪以来发展最为迅速、对人类生产生活影响最大的科技领域之一。”我国的北斗导航系统已开始为30多个国家提供服务，今年我国发射的神舟十二号载人飞船与天和核心舱完成自主快速交会对接……在这样的背景下，卫星运转问题无疑会成为高考命题的热点。在万有引力与宇宙航行的复习中，卫星间的“追击”和“相遇”问题让学生倍感头疼，由于卫星都在绕中心天体运转，学生往往找不到相对运动的关系。此时巧妙构建模型，分类研究，寻找通式，是解决这类问题的法宝。

一、基本模型巧构建

在同一平面内绕同一中心天体做匀速圆周运动的两卫星，当两卫星与中心天体三者共线时，两卫星的位置关系有两种特殊情况：一是两卫星在中心天体同侧，即两卫星相距最近；二是两卫星在中心天体两侧，即两卫星相距最远。

如图1，两卫星a、b在同一平面内绕同一个中心天体c做匀速圆周运动，且两卫星a、b的运转方向相同。据，可得周期可知Ta＜Tb，即a的转动比b快。从两卫星相距最近开始计时，a比b每多转一圈，即圆心角每多转过2π弧度，a、b相距最近一次，则两卫星再次相距最近的计算模型可按以下分析过程构建。

图1

从两卫星相距最近开始计时，设经过时间t，两卫星再次相距最近，则两卫星运动（即两卫星转过的圆心角）满足关系式t=2nπ，(n＝1，2，3……)，即t时间内a转过的圆心角比b多2π的整数倍，化简为(n＝1，2，3……)，即t时间内a比b多转了整数圈。

同理可知，从两卫星相距最近开始计时，到两卫星相距最远时，则两卫星运动关系满足关系式即t时间内a转过的圆心角比b多π的奇数倍。

【方法提炼】

同向相遇做起点，小圆转快大圆慢；多转一周为最近，多转半周距最远；圆周多解心默念，一近一远交替现。

二、模型深化求时间

高考题目对同一模型的考查并不是一成不变的，会依托基本模型而变化。

如图2，两卫星a、b与中心天体c的连线间夹角为θ，且两卫星a、b运转方向相反，a顺时针转动，b逆时针转动，求由图示位置开始，a、b相距最近和最远的时刻。

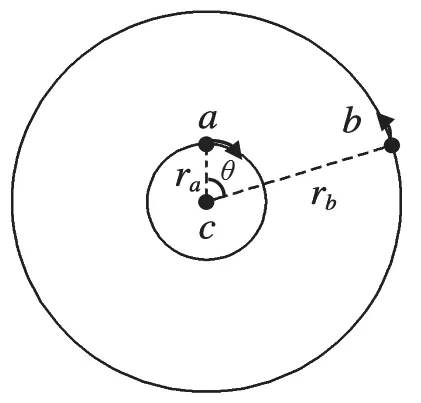
图2

分析：当a、b转过的角度之和等于θ 时，第一次相距最近。设相距最近的时刻为t1，应满足关系式相距最远的时刻为t2，应满足关系式再如，三颗不同轨道的地球卫星在同一平面的运动，可以先计算卫星两两之间的最短相遇时间，再综合考虑三颗卫星同时相遇的最短时间。如图3所示，a、b、c为地球赤道平面内绕地球做同向圆周运动的三颗卫星，a、b为中轨道卫星，它们的运行周期分别为6h和8h，c为地球同步卫星。某时刻，三颗卫星和地球在同一条直线上且彼此相距最近，求三颗卫星下一次与地球在同一直线上且彼此相距最近需要的时间。

思路：先计算卫星两两之间的最短相遇时间，再求时间的最小公倍数，即为四者共线的最短时间。

设b和c每相隔t1时间相距最近一次，则解 得t1=12h。同 理，a和c相距最近一次的时间t2=8h，a和b相距最近一次的时间t3=24h。再求t1、t2、t3的最小公倍数为24h，即为所求时间。其实t1、t2、t3三个时间任意取两个时间求最小公倍数即可，没必要把三个时间都计算出来。

【方法提炼】

反向运动也不难，变减为加同理断；

多个卫星齐上阵，公倍数中取时间。

三、模型拓展求共线

在基本模型的基础上，题目经常由求解时间转变为求解卫星共线的次数问题。如图3，若已知Ta:Tb＝1:k（k>1），则从图示位置开始，在b转动一周的过程中，求a、b、c共线的次数。只需分析出无论是相距最近还是最远，都满足共线，即a比b每多转过π弧度（每多转半圈），a、b、c共线一次。

图3

再对结果的表达式分析：当k为整数时，例如，k=8时，共线的次数p=14次；当k不是整数时，p的值可能也不是整数，只需舍掉小数部分即可，因为小数部分不够一次，例如，k=8.4时p=14.8，取14次；k=8.6时p=15.2，取15次。

有了基本的解题思路，再遇到类似题型，比如初始时刻a、b不在相距最近的位置上时，可以把以上模型的结论迁移过来使用。如图4，在同一平面内a、b绕c沿着逆时针方向做匀速圆周运动，若零时刻a、b两卫星分别与c的连线有一定夹角θ（a比b超前θ），已知已知a、b周期之比Ta:Tb=1:8，则从图示位置开始，求b运动一周的过程中，a、b、c共线的次数。

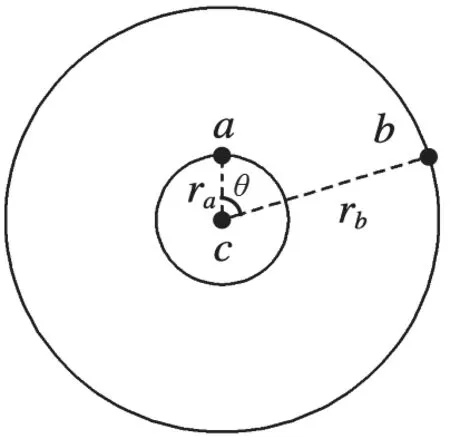
图4

分析时，先计算至第一次共线的时间t0，则 满 足代 入数据解之后的分析同前述，即Tb时间内到t0第一次共线后，又共线的次数为次，舍去小数部分取13，再加上第一次，共14次。

【方法提炼】

最近最远皆共线，次数只取整数算；超前滞后不用烦，转到共线做起点。

四、模型迁移灵活变

新高考改革后，试题阅读量增大，往往以实际情境为背景来命制试题。比如极地卫星轨道会以信息的形式呈现在题目中。具体实例如下：气象卫星、导航卫星、地球资源卫星等需要在全球范围内进行观测和应用，需要卫星运行时能到达南北极区上空，即卫星能飞经全球范围的上空，这样的卫星叫极地卫星。它的轨道平面与赤道面夹角为90°。

如图5，极地卫星a的圆轨道半径为r，周期为2h。赤道卫星b（轨道平面为赤道平面）的圆轨道半径为4r，求两卫星从距离最近到下一次最近的时间。

图5

求解前，先由信息构建出模型，两颗地球卫星轨道在相互垂直的平面上，再求相距最近的时间。求两卫星从相距最近到之后任意一次最近的时间，这个时间将不再是多转整数圈的所有取值了，由于两卫星相距最近的位置只能是两个轨道平面的交点，即两个特定位置上，其两位置间的时间差为每个卫星周期的一半，因此决定了相距最近的时间间隔。除了上述条件外，还要满足要么同为两卫星周期的整数倍，要么同为两卫星半周期的奇数倍。此题的结果t＝16h，赤道卫星运转1个周期，极地卫星运转刚好是8个周期，两卫星都转了整数圈。

再回归到相同的轨道平面，太阳系八大行星绕太阳运转的轨道几乎在同一平面内，地外行星的“冲日”“合日”与卫星相距最近与最远的模型不谋而合。如图为地外行星“冲日”与“合日”的示意图，“冲日”即地外行星运行到与太阳、地球形成一条直线的状态，按行星、地球、太阳的顺序排列，地球在中间，对应模型中太阳为中心天体，两行星相距最近。同理，“合日”即两行星相距最远。

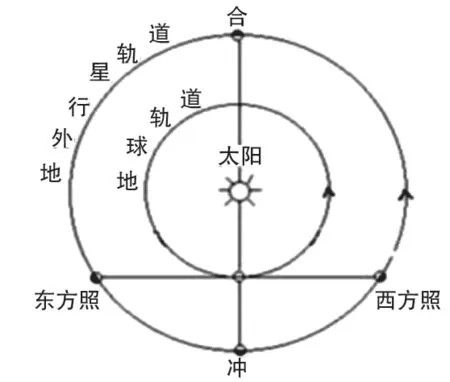
图6

以木星冲日为例，木星与地球几乎在同一平面内沿同一方向绕太阳做近似匀速圆周运动，木星到太阳的距离大约是地球到太阳距离的5倍，地球公转周期T1＝1年，木星公转周期年。设 经 时间t，再次出现木星冲日，则有t=2π，解得t≈1.1年。

大约每过1年零34天出现一次木星冲日，2019年6月10日出现木星冲日天象后，2020年7月14日再次出现，由此可推算2021年出现木星冲日的时间。

【方法提炼】

垂直轨道找两点，半周期下做推演；

合日冲日情境现，你追我赶都是圆。

基本模型是模型构建的基石，我们发现，无论是求解卫星相距最近、最远的时刻，还是求共线的次数，或是由冲日、合日求解时间，毫无疑问，它们都是同一模型的演变和延伸，解题思路相同，最终都归结为求解环绕星体转过的角度差问题。这样就实现了回归本真、多题归一的目的，也大大降低了学生理解上的难度。

在教学过程中，教师应加强学生模型思维的培养，帮助学生学习和掌握物理知识，掌握物理模型构建的方法，培养学生的物理核心素养。高考试题的情境往往比较灵活，可能以时事科技、天文奇观、航空航天等为背景设置试题，考查学生从所给材料中获取有效信息和灵活运用知识解决问题的能力。因此，我们可以以此为突破口，引导学生认真审题，正确构建物理模型，分析所用的物理规律，然后运用所学知识，进行演绎归纳、综合分析、迁移变化，最后准确规范地作答。窥一斑而知全貌，将其解题方法和思维应用到其他物理模型，举一反三，触类旁通，打造高效物理课堂，进一步提升学生的核心素养。