Existence of Positive Solutions for theNonhomogeneous Schrödinger-Poisson System with Strong Singularity
LIAO Jiafeng ,CHEN Qingfang and ZHU Lijun
1 College of Mathematics Education,China West Normal University,Nanchong 637002,China.
2 School of Mathematics and Information,China West Normal University,Nanchong 637002,China.
Abstract. In this paper,a class of nonhomogeneous Schrödinger-Poisson systems with strong singularity are considered.Combining with the variational method and Nehari method,we obtain a positive solution for this system which improves the recent results in the literature.
Key Words:Schrödinger-Poisson system;strong singularity;positive solution;Nehari method.
1 Introduction and main result
Consider the following nonhomogeneous Shrödinger-Poisson system involving singularity
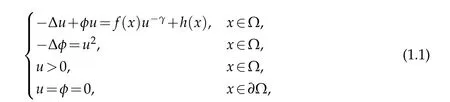
where Ω is a bounded domain in R3with smooth boundary∂Ω,γ∈(1,∞)andf∈L1(Ω)is a positive function,is nonzero and nonnegative.
Very recently,Yu and Chen considered system(1.1)withh≡0,and obtained a unique positive solutions,see[1].The singular Shrödinger-Poisson system was first studied by Zhang[2].When 0<γ<1,by using the variational method,she obtained a unique positive solution for system(1.1)withf(x)=µ>0,h(x)≡0.Recently,Lei and Liao generalized Theorem 1.1 in[2]to the critical case of system(1.1),and obtained two positive solutions by the variational method and Nehari manifold method,see[3].
The idea of system(1.1)is inspired by the following singular semilinear elliptic equation
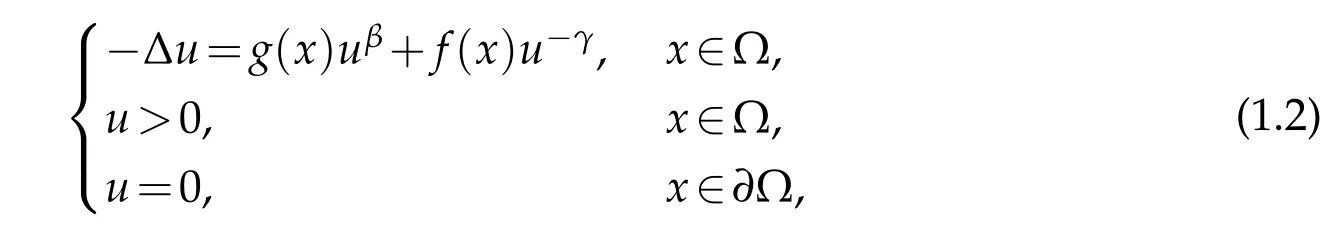
where Ω is a bounded domain in RN(N≥3) with smooth boundary∂Ω,β>0,fandgare positive functions with some certain conditions.Problem(1.2)arises in the study of non-Newtonian fluids (in particular pseudoplastic fluids),boundary-layer phenomena for viscous fluids (see [4,5]),in the Langmuir-Hinshelwood model of chemical heterogeneous catalyst kinetics (see [6]),in enzymatic kinetics models (see [7]),as well as in the theory of heat conduction in electrically conducting materials (see [8]) and in the study of guided modes of an electromagnetic field in nonlinear medium(see[9]).When 0<γ<1,many papers have extensively studied problem(1.2),see for examples[10-21].Particularly,Sun,Wu and Long studied the multiplicity positive solutions for the singular elliptic problem for the first time in[20].Very recently,Wang and Yan considered the case ofγ=1,by using the approximation method,they obtained a unique result,see[22].
While the case of problem (1.2) withg(x)≡0 andγ>1 is first considered by Lazer and Mckenna[23],they obtained that problem(1.2)has a unique solutionu−γ∈C2+α(Ω)∩C(Ω) for anyγ>0 andf∈Cα(Ω) withf(x)>0(x∈Ω),andu−γ∈H10(Ω) if and only ifγ<3.In this direction,Boccardo and Orsina[24]studied problem(1.2)withg(x)≡0 andf∈L1(Ω)is nonnegative,and obtained a solutionfor anyγ>1.More recent development,wheng∈L∞(Ω)and 0
To our best knowledge,the strong singular Schrödinger-Poisson system has not been studied up to now,except for [1] and [27].Inspired by [2,23,24],we consider system(1.1)withγ>1,that is,the strong singular Schrödinger-Possion system.The main result can be described as follows.
Theorem 1.1.LetΩ ⊂R3be a bounded domain with smooth boundary ∂Ω.Assume that γ∈(1,+∞)and f∈L1(Ω)is positive,and h∈L65(Ω)is nonzero and nonnegative.Then,system(1.1)possesses at least one positive solutionif and only if there existssuch that

Remark 1.1.On the one hand,compared with[2],we complete Theorem 1.1 in[2]with the strong singular Schrödinger-Poisson system.On the other hand,we generalize the casea=1,b=0 of[27]and[1]to system(1.1).
Moreover,when system(1.1)reduces to the following singular elliptic equation

we also can prove that problem(1.4)has at least one positive solution if and only if(1.3)holds.We generalize[25]to the case ofq=0.
2 Proof of Theorem
With the help of the Lax-Milgram theorem,for everyu∈H10(Ω),the second equation of system (1.1) with Dirichlet boundary condition has a unique solutionφu∈H10(Ω),we substituteφuto the first equation of system (1.1),then system(1.1) can be transformed into the following one variable problem

Note that a functionis called a weak solution of problem(2.1),that is(u,φu)is a weak solution of system(1.1)andu>0 satisfying

For all,the energy functional associated with problem(2.1)is defined by

The Sobolev spaceis endowed with the normdenotes the norm ofLs(Ω).For readers’convenience,we give the following conclusions aboutφufrom[2].
Lemma 2.1.For every,there exists a uniquesolution of
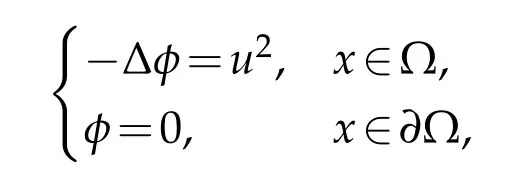
and φu satisfies the following properties:
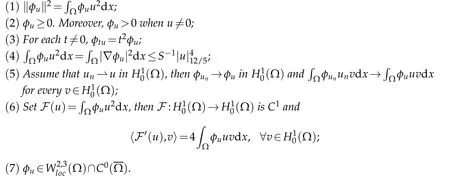
Sinceγ>1,the functionalIis not well defined onH10(Ω).In order to obtain the solution of problem(2.1),we define the following two constrained sets:
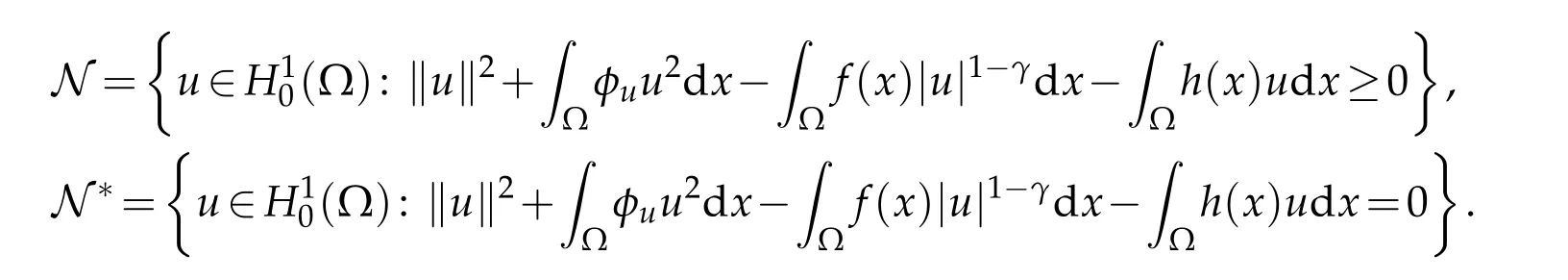
Now,we have the following properties for the above two constrained sets.
Lemma 2.2.Assume that γ∈(1,+∞)and(1.3)holds,thenNandN∗are nonempty.Moreover,Nis an unbounded closed set in
Proof.According to (1.3),for anyt>0 andwe defineJu(t)by

where the property(3)of Lemma 2.1 is used.Then,one has

Now,we prove that N is a closed set.Assume{un}⊂N withthen we should proveu∈N.Since

it follows from Lemma 2.1 and Fatou’s Lemma that

which implies thatu∈N.Then,the proof of Lemma 2.2 is completed.
Lemma 2.3.For any u∈N∗and,ϕ>0,there exist ε>0and a continuous function t=t(s)>0(s∈R),for every|s|<ε satisfying t(0)=1,t(s)(u+sϕ)∈N∗,∀s∈R,|s|<ε.
Proof.For anyu∈N∗,we defineF:R×R→R by

Then,applying the implicit function theorem toFat the point(1,0),we can obtainε>0 and a continuous functiont=t(s)>0(s∈R)satisfyingt(0)=1,t(s)(u+sϕ)∈N∗for anys∈R with|s|<ε.This completes the proof of Lemma 2.3.
Now,we have the following conclusion.
Theorem 2.1.Suppose that γ∈(1,+∞)and f∈L1(Ω)is positive,andis nonzero and nonnegative,then problem(2.1)has at least one positive solutionif and only if f satisfies(1.3).
Proof.Obviously,the necessity is true.Now,we only need prove the sufficiency.Obviously,Iis coercive and bounded from below onThus,m=infu∈NI(u) is well defined.Since N is closed,we can apply Ekelands variational principle to this minimization problemm,there exists a sequence{un}⊂N satisfying the following properties:
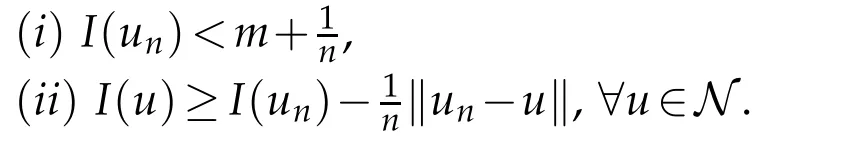
Thanks toI(|u|)≤I(u),one has that{|un|}satisfies the properties(i)and(ii).So,we can assume from the beginning thatun≥0 in Ω.Sinceun∈N,one has
which implies thatun(x)>0 a.e.x∈Ω.Obviously,{un} is bounded inGoing if necessary to a subsequence,still denoted by {un},there existswithu∗≥0 such that

asn→∞.Sinceun∈N again,combining with the property(5) of Lemma 2.1 and(2.3),by Fatou’s Lemma,one has
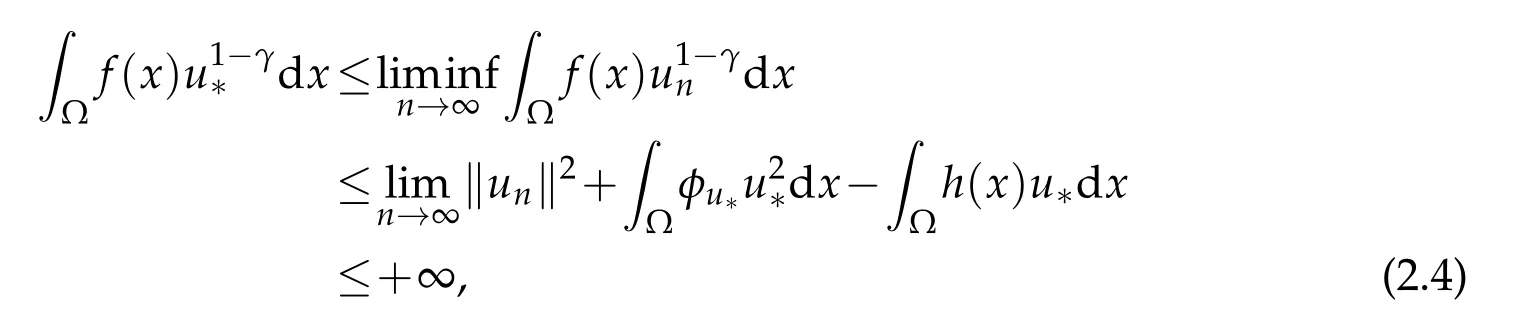
which implies thatu∗(x)>0 a.e.x∈Ω.Now,we will prove thatu∗∈N∗andI(u∗)=m.We divide the following two cases to prove it.
Case 1.Assume that{un}⊂NN∗for allnlarge enough.Letwithϕ≥0.Since{un}⊂NN∗andγ>1,for anyt≥0,one has

Consequently,by the continuity,we can chooset>0 small enough such that

which implies that(un+tϕ)∈N fort>0 small enough.Thus,according to(ii),we have

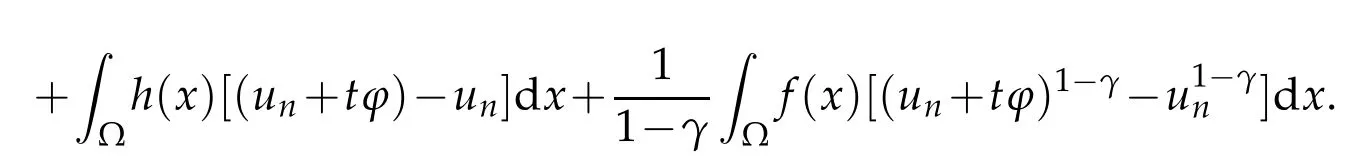
Consequently,dividing the inequality byt>0 and passing to the infimum limit,it follows from Fatou’s Lemma and the property(6)of Lemma 2.1 that
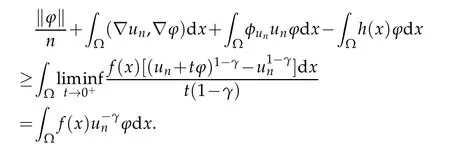
Passing to the infimum limit to the above inequality,letn→∞,by the property (5) of Lemma 2.1 and Fatou’s Lemma again,one obtains
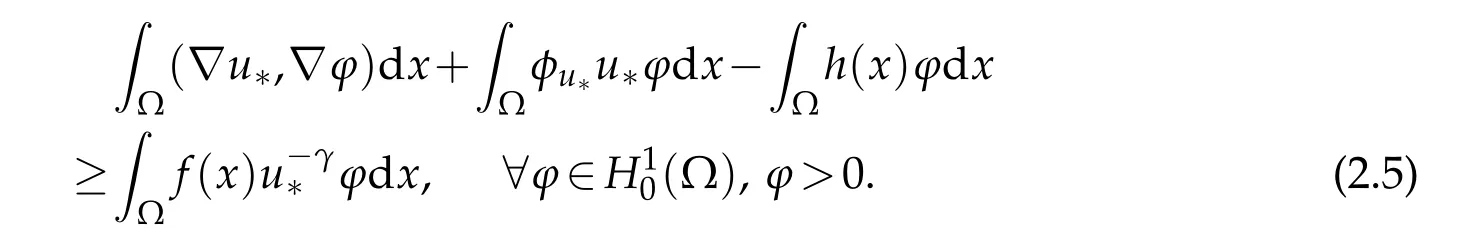
Sinceu∗(x)>0 a.e.x∈Ω,choosingϕ=u∗,one hasu∗∈N.Consequently,according to the argument in Lemma 2.2,there exists a unique positive constantt(u∗) such thatandt(u∗)u∗∈N∗.Then,we have
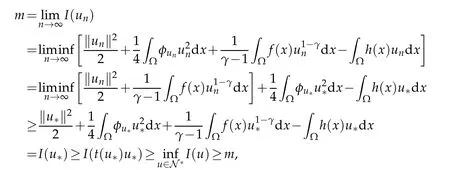
which implies that

Case 2.There exists a subsequence of{un},still denoted by{un},such that{un}⊂N∗.Letwithϕ≥0.Applying Lemma 2.3 withu=unands>0 small enough,we find a sequence of continuous functionstn=tn(s)such thattn(0)=1 andtn(s)(un+sϕ).Noting thattn(s)(un+sϕ)∈N∗andun∈N∗,one has
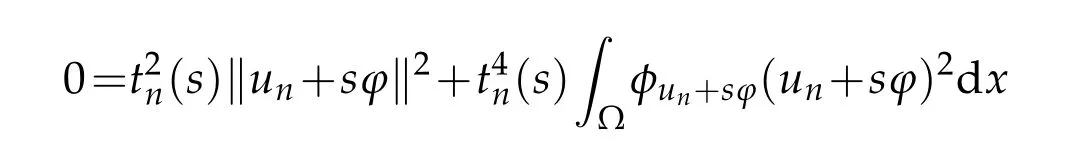

Consequently,it follows from(2.7)and(2.8)that

Then dividing bys>0,sinceγ>1,one has
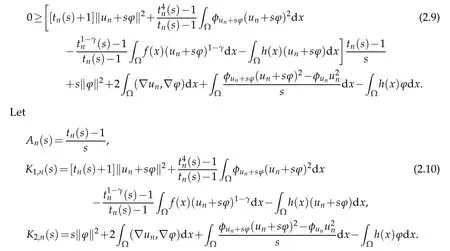
Then,according to(2.8)and Lemma 2.1,one has

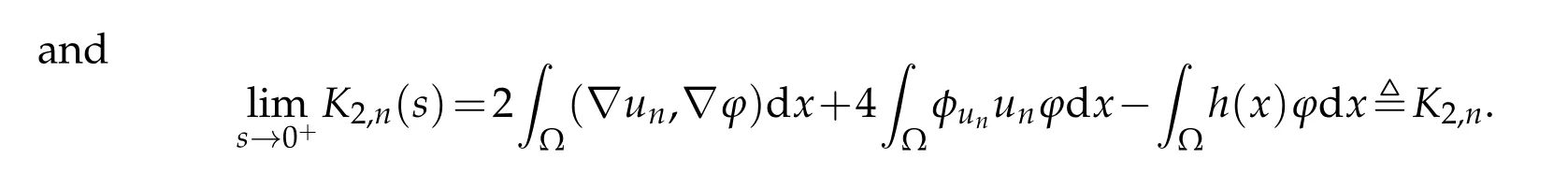
Since{un}is bounded in,there exist positive constantsC1andC2such thatK1,n
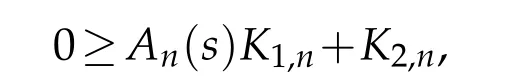
which implies thatAn(s) is bounded from above uniformly inn.Thus,there exists a constantC3>0 such that

forn∈N+large enough.
On the other hand,we will prove thatAn(s)is bounded from below uniformly inn.By the subadditivity of norm,one has

Thus,by condition(ii),it follows from(2.7)and(2.8)that
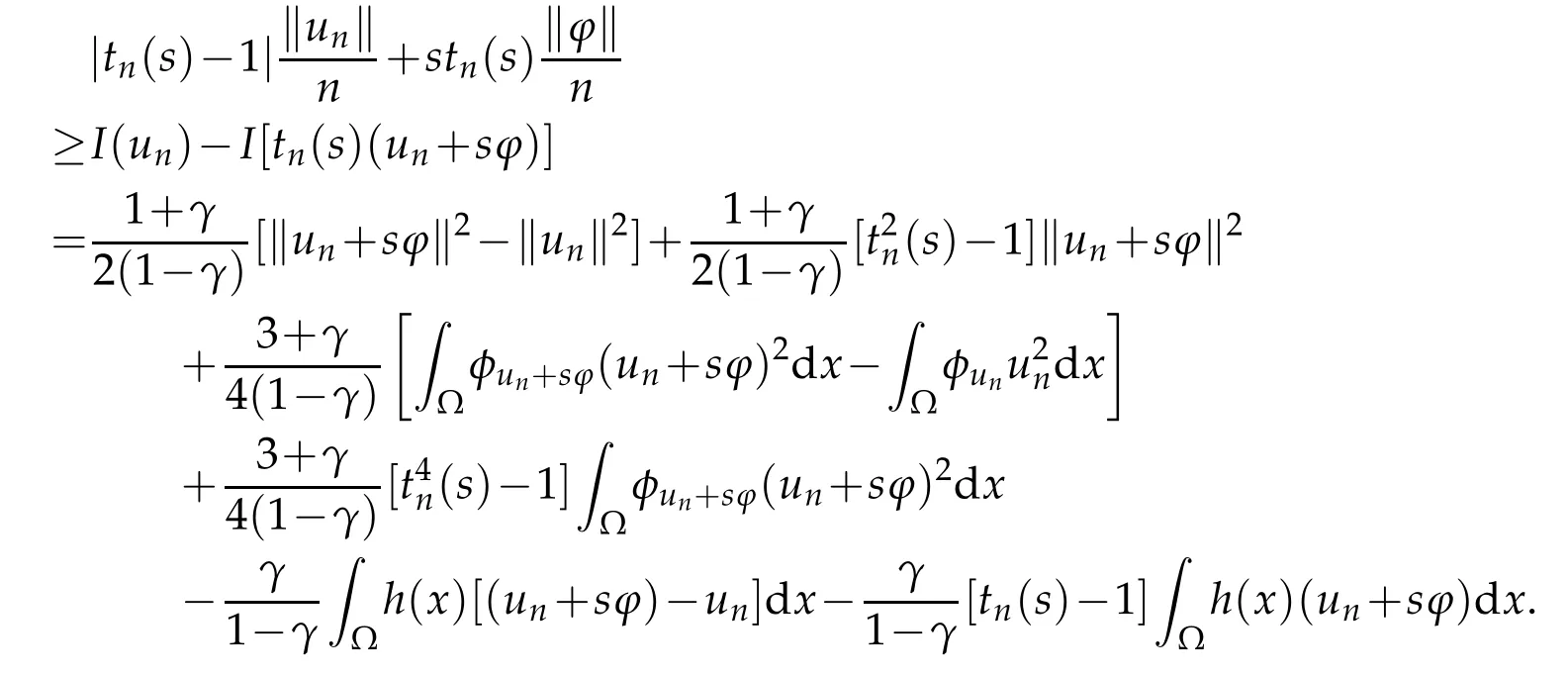
Then dividing bys>0,it follows that

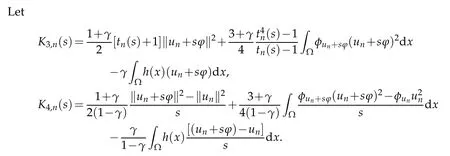
Then,from Lemma 2.1,we obtain
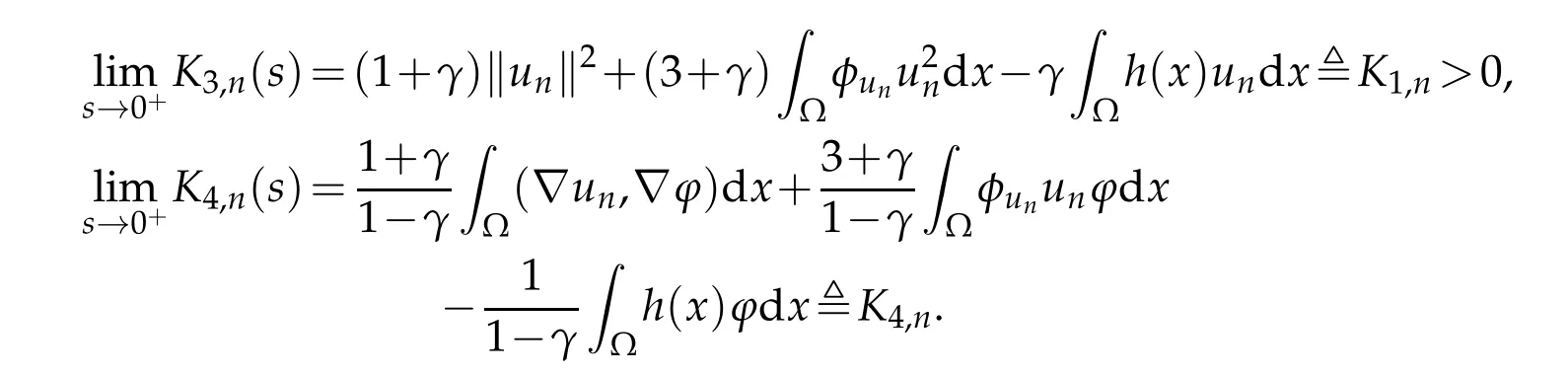
Consequently,from(2.12),we have
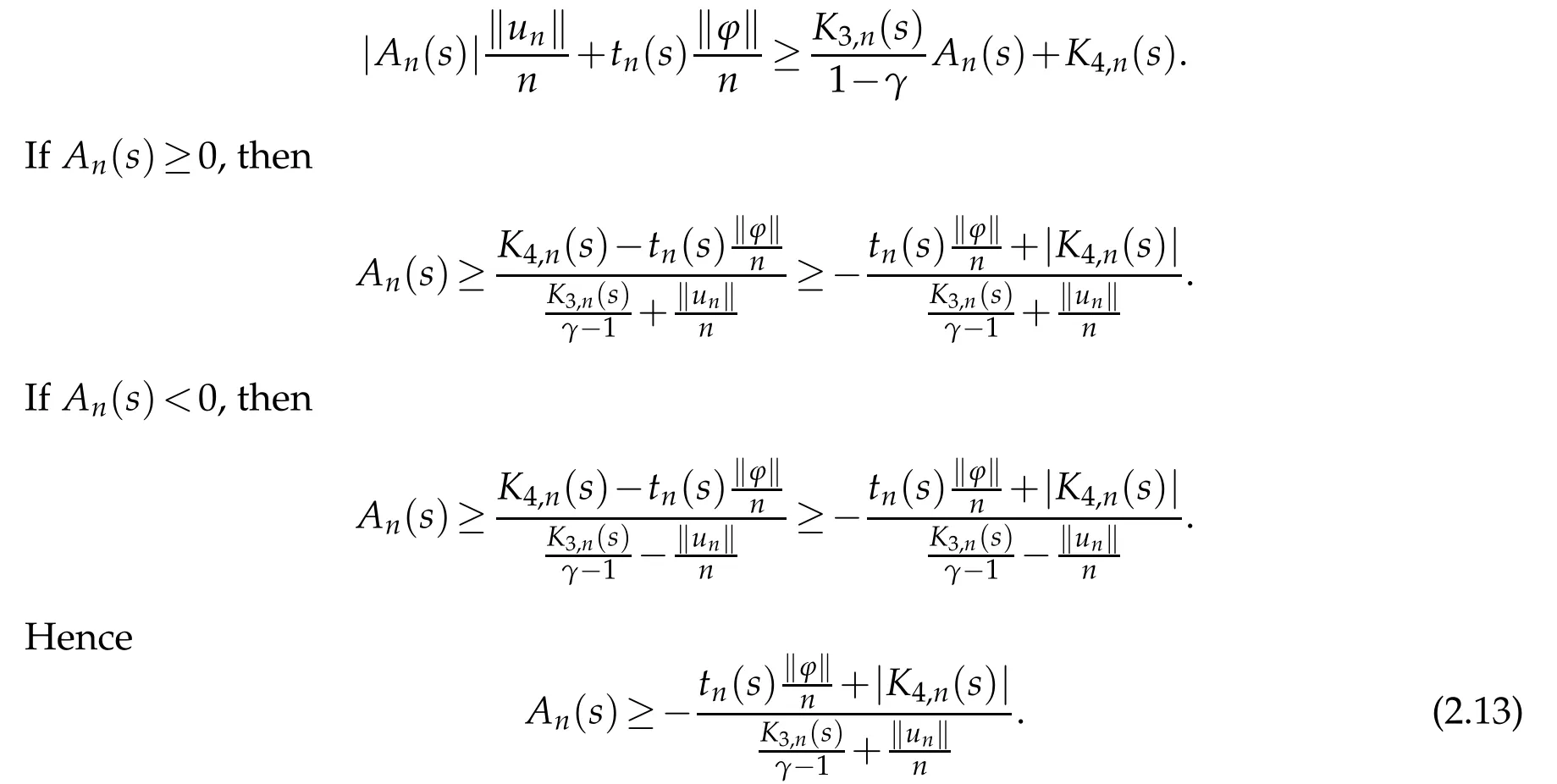
By the boundedness of{un}again,there existsC4>0 such that|K4,n| forn∈N+large enough.Thus,according to(2.11)and(2.14),it follows that there exists a constantC5>0 such that forn∈N+large enough. By the subadditivity of norm and(ii)again,we can obtain and dividing bys>0,we get From(2.8)and Lemma 2.1,one gets It follows from(2.16)that Sinceγ>1,by Fatou’s Lemma,it follows from(2.17)and(2.15)that fornlarge enough.Consequently,applying Fatou’s Lemma again,one obtains Particularly,choosingϕ=u∗in(2.18),one hasu∗∈N.Moreover,by the same argument in Case one,we can derive that Finally,we will prove thatu∗is a solution of problem (2.1).From (2.5),(2.6),(2.18)and(2.19),we have the desired conclusion in all possibilities thatu∗∈N∗and Sincemeas{x∈Ω:u∗+εψ≤0}→0 asε→0+,the above inequality dividing byεand lettingε→0+,one obtains for all.Hence,this inequality also holds equally well for −ψ.It follows that for allThus,u∗is indeed a positive solution of problem(2.1).This completes the proof of Theorem 2.1. Acknowledgements Supported by the Scientific Research Fund of Sichuan Provincial Education Department(18ZA0471),Fundamental Research Funds of China West Normal University (18B015)and Innovative Research Team of China West Normal University(CXTD2018-8).The authors express their gratitude to the reviewers for careful reading and helpful suggestions which led to an improvement of the original manuscript.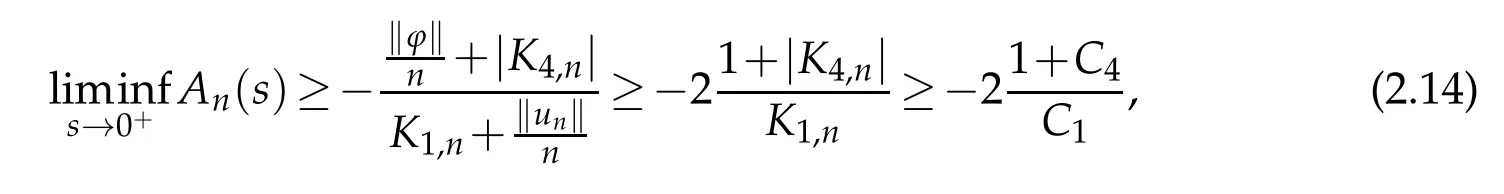



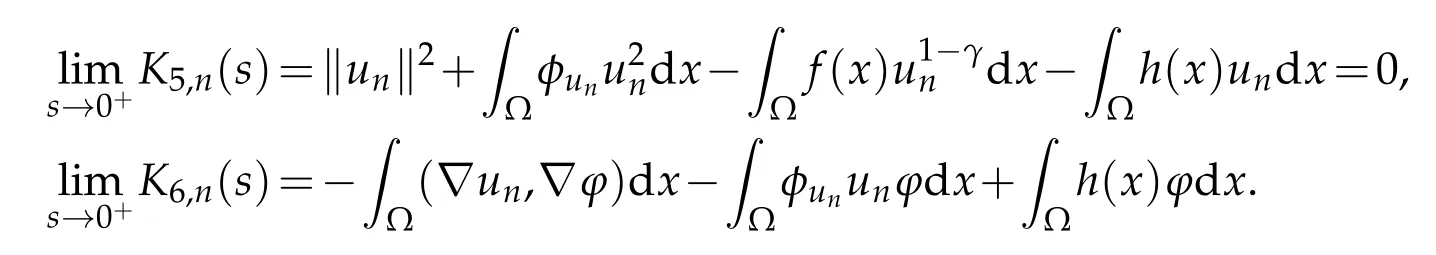

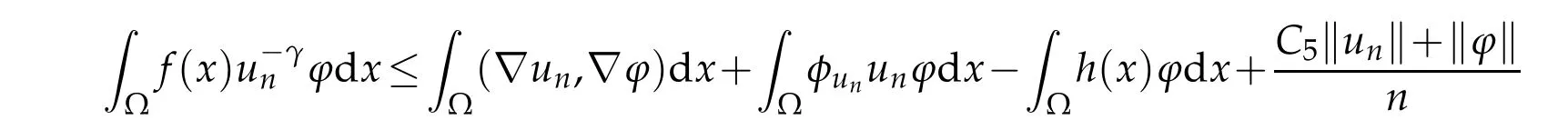
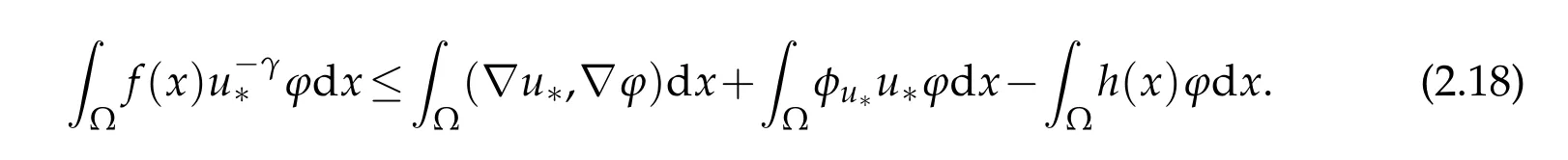

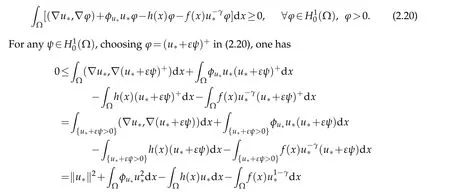


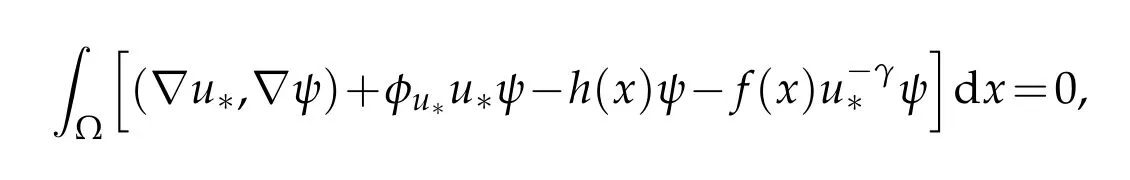
 Journal of Partial Differential Equations2021年2期
Journal of Partial Differential Equations2021年2期
- Journal of Partial Differential Equations的其它文章
- Global Attracting Sets of Neutral Stochastic Functional Differential Equations Drivenby Poisson Jumps
- Trudinger-Moser Type Inequality Under Lorentz-Sobolev Norms Constraint
- Asymptotic Behavior in a Quasilinear Fully Parabolic Chemotaxis System with Indirect Signal Production and Logistic Source
- Conditional Regularity of Weak Solutions to the 3D Magnetic B´enard Fluid System
- On Existence of Local Solutions for a Hyperbolic System Modelling Chemotaxis with Memory Term
