基于BP神经网络的能见度估测研究

金钊,邱康俊,张苗苗

(1 合肥市气象局市公共气象服务中心,安徽 合肥 230031;2 安徽省气象信息中心运行监控科,安徽 合肥 230031)

0 引言

大气能见度一般定义为视力正常的人在当时天气条件下能够从天空背景中看到和辨认黑色目标物的最大水平距离[1],它是表征大气透明度的重要物理量。大气能见度与人们的日常生活密切相关,低的大气能见度极易导致交通事故发生,造成人民群众的生命和财产损失。因此大气能见度的预测研究,对减少交通事故,保障人民群众生命财产安全具有重要意义。

大气能见度定量计算理论基础源于1924 年Koschmieder 提出的视程理论[2],其核心是将能见度V与大气消光系数σ 联系起来。结合Bouguer-Lambert 定律,并取对比视感阈ε=0.02,得出大气水平能见度公式为V=3.912/σ。由此可见,大气消光系数σ 是影响大气能见度的直接因子,σ 越大,大气能见度越低,说明大气越混浊,其消光效应越强。在可见光和近红外波段,粒子散射是大气消光的主要因素[3],而基于Mie 散射理论的大气消光效应是复杂的非线性物理过程,因此直接计算大气消光系数异常困难。研究表明低能见度的形成受多种条件综合影响,主要包括气象条件、地形条件及人类活动等[4−8]。各种自然条件下,时空差异和分布不均以及强烈人类活动对消光系数影响的不确定性,造成了大气能见度变化的不确定性,利用一般的线性模型难以准确地预测大气能见度变化。

随着计算机技术的不断更新进步,人工神经网络(Artificial neural network,ANN)得以快速发展。基于人工神经网络特性,人们在不用构造复杂非线性模型的情况下,可以利用人工神经网络对复杂非线性系统进行模拟研究。Back propagation(BP)神经网络是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。蔡子颖等[9]利用BP 神经网络对CUACE 和BERMPS 模式能见度预报产品进行改进,试验结果表明BP 神经网络能见度预报能够消除天津地区能见度预报的平均偏差,与CUACE 和BERMPS 模式最优结果比较,能够使天津能见度预报与实况之间相关系数提高7%,相对误差减少32%。包红军等[10]基于BP 神经网络算法对京珠高速公路能见度等级进行预测研究,建立了京珠高速公路低能见度(雾)神经网络预测模型,模型预测能见度整体检验合格率达到78.8%,且能见度达三级(0.501∼1 km)时检验结果最好,合格率达到87%[2]。因此在不用直接计算大气消光系数的情况下,可以利用人工神经网络对大气能见度进行模拟研究。

大气能见度是污染物和气象参数综合作用的结果,尤其是受风、温度和相对湿度的影响。本文利用安徽省高速公路实时监测系统提供的观测资料,在假设该观测站大气污染物来源稳定的条件下,应用BP 神经网络对大气能见度进行模拟研究,探索高速公路短时能见度的估算方法,为高速公路监测预警提供进一步支撑。

1 数据来源与研究方法

1.1 数据来源

研究数据来源于安徽省高速公路实时监测系统分钟观测数据,包括雨量、气温、平均风向、平均风速、瞬时风向、瞬时风速、极大风向、极大风速、相对湿度、能见度。山区较易形成低能见度天气,对高速公路交通安全影响较大。

1.2 BP 神经网络

BP 神经网络是ANN 建模的基本网络,是神经网络中一种反向传递并能修正误差的多层映射网络。一般BP 神经网络包含三层结构:输入层、隐含层和输出层,层与层之间的神经元采用全互连的模式,通过相应的网络权重系数相互联系,每层内的神经元没有连接。当参数适当时,此网络能收敛到较小的均方差,寻找到最优解。

1.3 检验方法

利用平均偏差D、相对误差δ、均方根误差ERMS和相关系数R等统计指标对模拟效果予以检验分析,其计算公式分别为

式中:Co为观测值,Cp为模式模拟值,表示所有数据的平均,σo、σp分别表示观测值和模拟值的标准差。

2 模拟研究

2.1 模型数据选取

气象服务中,对高速公路能见度短时间的变化,特别是从高能见度转变为低能见度的变化最为敏感。因此本研究主要模拟大气能见度特别是低能见度天气过程的变化。为保证能见度数据的完整性和连续性,样本数据的选择在时间上要求连续,值域范围能够包含1000 m 以下的低能见度数据,且应包含整个连续的低能见度演变过程。据统计,G 长岭关站(115.50◦N,31.30◦E)年发生低能见度过程约150 余次,且该站2013年数据较为连续,因此选择该站2013 年分钟观测数据作为原始资料进行研究。对分钟数据各要素进行界限值和内部一致性检查预处理后,再进行分析处理。G 长岭关站2013 年各月大气能见度与气温等观测要素的相关系数如表1 所示。对表中的相关系数进行分析,选取气温、平均风速、瞬时风速、极大风速、相对湿度作为BP 神经网络输入层,能见度为输出层。

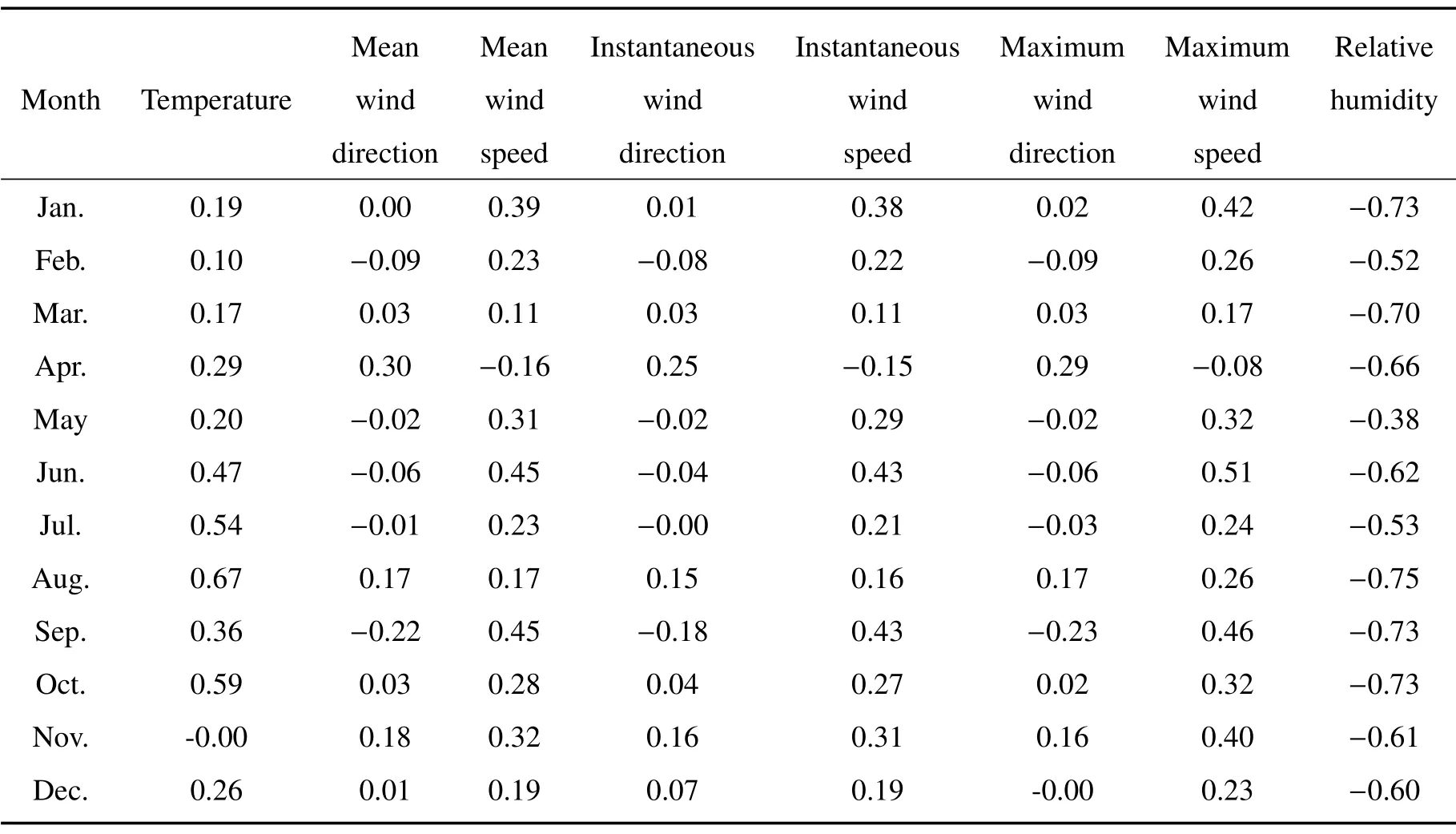
表1 各月各要素与大气能见度的相关系数Table 1 Correlation coefficients between various elements and atmospheric visibility in each month

2.2 模型训练及检验

为试验BP 神经网络的训练效果,在样本选择时,顺序样本保留了各要素的时间连续性,而随机样本在剔除时间连续性同时,可以重点研究低能见度样本的训练效果。以顺序样本和随机样本分别进行试验,检验模型输出与样本的相对误差和相关系数。

2.2.1 顺序样本试验

以2013 年4 月1–30 日原始观测能见度数据为训练对象,步长为3 h,将数据输入BP 神经网络进行滚动训练。每一次训练,选取前3 天的分钟数据为一次训练样本,后3 h 分钟数据为该次训练的验证样本,若验证样本的模型输出与实际样本相关系数绝对值大于0.8,结束本次训练;若相关系数绝对值小于0.8,则重新训练本次样本,训练回数上限为10 回。即相同样本在10 回训练后相关系数绝对值还是小于0.8,则结束本次样本训练,以3 h 为步长向后滚动重新选取样本进行训练。

图1 为2013 年4 月顺序样本试验的相对误差直方图及累积百分比图。横坐标是试验结果与实际观测值的相对误差;左边纵坐标为频次,即在该相对误差的样本数;右边纵坐标为对应相对误差的累积百分比。由图可知,相对误差在−20%∼20%以间的占总试验次数的68.6%。表2 为随机样本试验相关系数(Correlation coefficient)出现频率(Frequency)及对应的累计百分比(Cumulative percentage)。由表可知,相关系数绝对值大于0.5 的占总试验次数的38.24%。

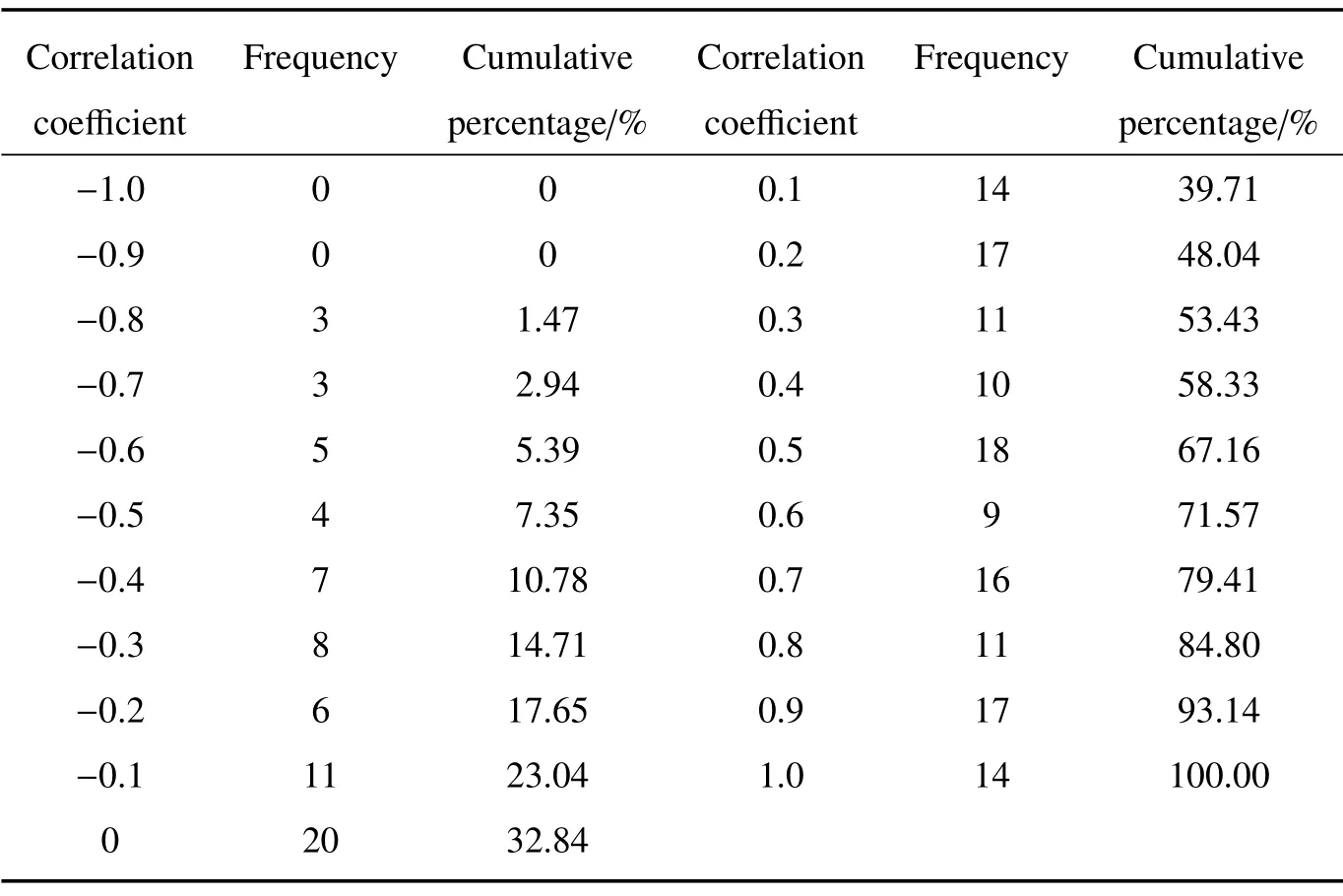
表2 顺序样本试验相关系数出现频率及累积百分比Table 2 Occurrence frequency of correlation coefficient and cumulative percentage for sequence sample test

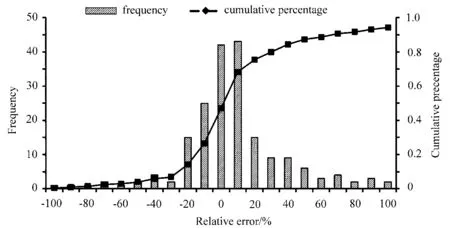
图1 顺序样本试验相对误差直方图及累积百分比Fig.1 Relative error histogram and cumulative percentage for sequential sample test

因此在应用BP 神经网络,通过湿度、温度、平均风速、瞬时风速、极大风速作为BP 神经网络输入层,输出层为能见度进行试验时,整体试验数据偏差可以接受,但是模拟数据与样本数据总体试验相关性不理想,分析原因可能有两点:一是整个网络训练样本质量不高,有错误数据对训练产生影响;二是在能见度估算模拟时,神经网络训练参数可能不合适,需要对输入参数、训练函数等模型参数进行调整。

2.2.2 随机样本试验

同样以2013 年4 月数据为例。随机选取1440×3 组分钟数据为训练样本,180 组分钟数据为验证样本进行训练,总计训练20 次。当验证样本的模型输出与实际样本相关系数绝对值大于0.8 后结束本次训练。每次网络训练中,若相关系数绝对值小于0.8,则重新训练本次样本,训练回数上限为10 回,即相同样本,当相关系数绝对值在10 回训练后还是小于0.8,则结束本次样本训练,重新选取样本进行训练。

图2 是2013 年4 月随机样本试验的相对误差直方图及累积百分比图。同样横坐标是试验结果与实际观测值的相对误差;左边纵坐标为频次;右边纵坐标为对应相对误差的累积百分比。由图可知,相对误差都在40%以上,误差较大。表3 为随机样本试验相关系数出现频率及对应累积百分比。由表可知,可见随机样本20 次试验中,相关系数在0.6∼0.8 之间,说明各次试验中,BP 网络模拟输出与检验样本的相关性较好,趋势较为一致。

表3 随机样本试验相关系数出现频率及累积百分比Table 3 Occurrence frequency of correlation coefficient and cumulative percentage for random sample test

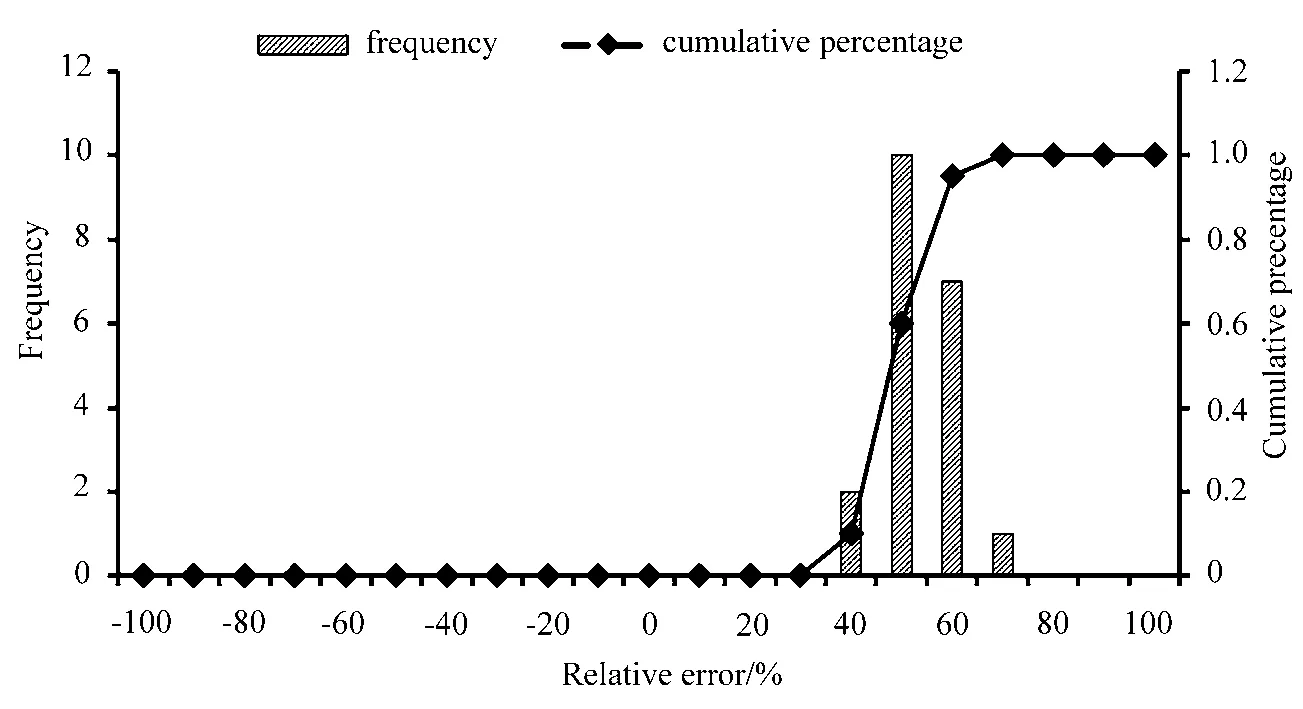
图2 随机样本试验相对误差直方图及累积百分比Fig.2 Relative error histogram and cumulative percentage for random sample test

2.2.3 低能见度随机样本试验

2013 年全年能见度小于3000 m 的所有数据为总样本,随机选取1440×3 组分钟数据为训练样本,180 组分钟数据为验证样本进行训练,总计训练200 次。当验证样本的模型输出与实际样本相关系数绝对值大于0.8 后结束本次训练。每次网络训练中,若相关系数绝对值小于0.8,则重新训练本次样本,训练回数上限为10 回,即相同样本,当相关系数绝对值在10 回训练后还是小于0.8,则结束本次样本训练,重新选取样本进行训练。

图3 为2013 年低能见度随机样本试验的相对误差直方图及累积百分比,横坐标是试验结果与实际观测值的相对误差;左边纵坐标为频次,即在该相对误差的样本数占总样本数的比;右边纵坐标为对应相对误差的累积百分比。由图可知,相对误差在200%以上的占总试验次数的94.5%。说明在低能见度随机试验中,模型输出与样本值的相对误差增大。推测可能的原因为:1)与样本本身数值较小有关。在差值相同的情况下,样本值越小,相对误差占比越大。因此在计算相对误差时,平均偏差微小变化就会引起相对误差较大的变化。2)环境因素影响,污染源的变化或局地污染过程。3)山地水汽较多,在气象条件合适的情况下,存在雾的生消过程。

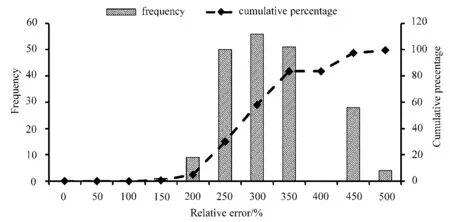
图3 低能见度随机样本试验相对误差直方图及累积百分比Fig.3 Relative error histogram and cumulative percentage for random low-visibility sample test

图4 为随机样本试验平均偏差及均方根误差(RMSE)变化,横坐标为试验序数,左边纵坐标为均方根误差,右边纵坐标为平均偏差。由图可知,200 次试验验证样本的平均偏差(模型输出与验证样本偏差的平均值)变化范围在0∼200 m 之间,绝对值最大为173.4 m,最小为0.59 m,平均为44.26 m,总体上模型输出值与样本值偏差不大,但其均方根误差主要集中在700∼850 m 之间,变化幅度不大,说明神经网络算法稳定。

图4 随机样本试验平均偏差及均方根误差变化图Fig.4 Variation graph of average deviation and root mean square error for random sample test

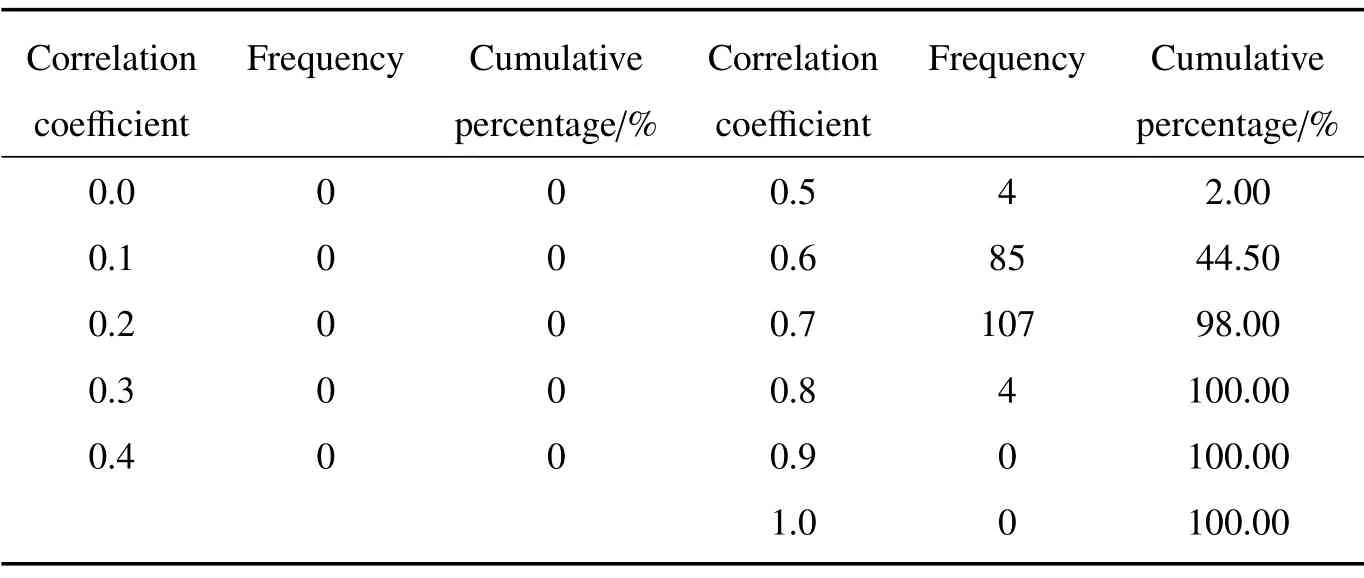
表4 低能见度随机样本试验相关系数出现频率及累积百分比Table 4 Occurrence frequency of correlation coefficient and cumulative percentage for low-visibility random sample test

3 结论

1)应用BP 神经网络,湿度、温度、平均风速、瞬时风速、极大风速作为BP 神经网络输入层,能见度作为输出层进行顺序样本试验,整体试验数据偏差在可接受范围内,相对误差在20%以内的占总试验次数的68.6%,但是模拟数据与样本数据总体试验相关性不理想,需要进一步提高训练样本质量,调整模型参数。

2)随机样本试验结果的相对误差均在40%以上,误差较大。但随机样本20 次试验中,相关系数均在0.6∼0.8 之间,说明各次试验中,BP 网络模拟输出与检验样本的相关性较好,趋势较为一致。

3)对低能见度随机样本进行试验,可能由于样本本身数值较小,在计算过程中,平均偏差微小变化即可引起相对误差大的变化,导致低能见度随机试验模型输出值与样本值相对误差增大,相对误差在200%以上的占总试验次数的94.5%。而模型输出与样本变差均方根误差主要集中在700∼850 m 之间,变化幅度不大,说明神经网络算法是稳定的。

高速公路能见度变化受多种因素影响,导致大气能见度变化具有不确定性,一般的线性模型难以准确预测。人工神经网络具有自适应、自组织、自学习能力,适用于复杂多变的非线性系统。建立了高速公路能见度BP 神经网络预测模型,通过对安徽省G 长岭关站2013 年分钟能见度数据进行实验,表明BP 神经网络预测高速公路能见度,具有一定的预测效果。