基于三维有限元的航空大地电磁倾子响应特征
刘彦涛,彭莉红,孙栋华,张伟盟,王海红
(1.核工业航测遥感中心,河北 石家庄 050002; 2.中核集团铀资源地球物理勘查技术(重点实验室),河北 石家庄 050002; 3.河北省航空探测与遥感技术重点实验室,河北 石家庄 050002)
0 引言
大地电磁法利用天然电磁场作为探测场源,具有探测深度大、设备轻便等优点[1]。为对高山、荒漠、沼泽地等勘探人员无法到达区域进行地球物理勘探,可选方法之一为运用航空器搭载测量仪器对这些区域进行探测,也因此航空大地电磁近些年得到了快速发展[2-5]。与传统大地电磁方法原理相同,航空大地电磁利用天然电磁场作为场源,接收由于地下地质体横向不均匀激励的垂直磁场分量,结合地面接收到的磁场水平分量,换算倾子参数,反演地下地质体电阻率分布,从而达到探测目的。远方天然电磁场可看作平面电磁波垂直入射到地面,只有当地质体存在横向电性变化时,才会激励起垂直磁场[6]。不同于传统大地电磁法,由于航空大地电磁空中探测无法接地,只能采集磁场分量,通过磁场分量可换算得到倾子参数,再利用倾子参数对地下地质体进行地球物理解释。
倾子是对地质体电性横向不均匀性的一种反映[7],由于磁场垂直分量强度小且受干扰大,早期大地电场法勘探中没有得到成功应用,1989年Labson提出远参考技术对原始数据进行降噪处理,并通过优化磁场接收装置,成功使用倾子参数进行了地球物理解释[8]。近些年对大地电磁倾子响应的研究较多[9-12],尤其是利用数值模拟算法模拟倾子对典型地电模型的响应特征,分析其响应规律[13-17],研究覆盖层、横向电阻率差异大小、地形、测线高度等因素对倾子的影响[18-20]。前人数值研究中所选测线大多垂直岩性分界面,使异常体倾子响应理想化,而在实际探测中,不能保证设计测线与所有横向地电断面垂直。本文首先简单介绍了航空大地电磁勘探原理以及航空大地电磁ZTEM探测系统,利用三维有限元方法对测区磁场分量分布特征进行模拟分析,之后建立典型地电模型,研究了当测线与横向地电断面斜交时的倾子响应特征。
1 方法原理
天然电磁场以平面波的形式垂直入射到地下,入射的平面电磁波中不存在磁场垂直分量,当地下地质体存在横向电性变化时,将会激励垂直磁场,这个垂直磁场与两个水平磁场存在复线性关系:
Hz(ω)=Tx(ω)Hx(ω)+Ty(ω)Hy(ω) ,
(1)
式中:Hx(ω)、Hy(ω)、Hz(ω)分别为不同频率x、y、z磁场分量,Tx(ω)、Ty(ω)为倾子系数。倾子是复数值且随频率变化。倾子参数与地下地质体电性分布相关而不与激发电磁波极化方向相关,所以倾子可以作为解释地下电性分布的参数。
在式(1)两边分别乘以Hx(ω)、Hy(ω)的共轭复数值[6],构建方程组:
(2)
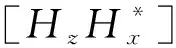
通过方程组(2)可求取倾子值Tx、Ty:
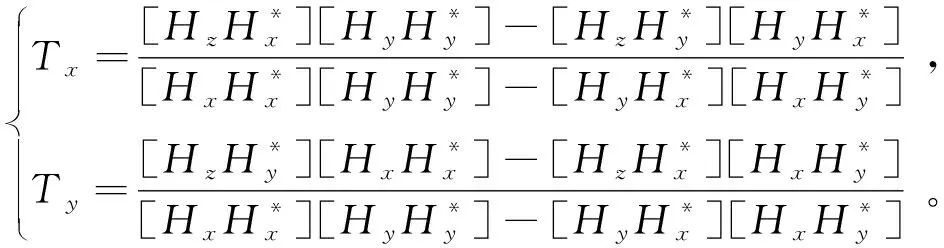
(3)
2 ZTEM系统
ZTEM系统是目前全球应用较为广泛的商用航空大地电磁系统,系统主要由两部分组成,如图1。

图1 ZTEM系统Fig.1 System of ZTEM
空中接收线圈用于接收磁场Hz分量,线圈直径7.4 m,考虑到直升机对接收信号的影响,同时保证飞行员的可操控性,线圈吊挂于直升机下方85 m处。线圈上安置3个GPS天线,实时监测线圈姿态,用于消除水平和垂直电磁场交叉耦合的效应。数据采集过程中控制线圈离地高度约100 m,飞机飞行速度80 km/h。
地面接收线圈主要是由3个正交的边长为 3.05 m的方形接收线圈组成,安置在工作区25 km范围内且人文干扰相对较小的固定地点,用来观测水平磁场分量Hx和Hy。基站5 km范围内最好无高压线通过,并且没有无线电基站、信号发射站等发射无线信号的装置。
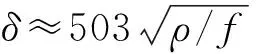
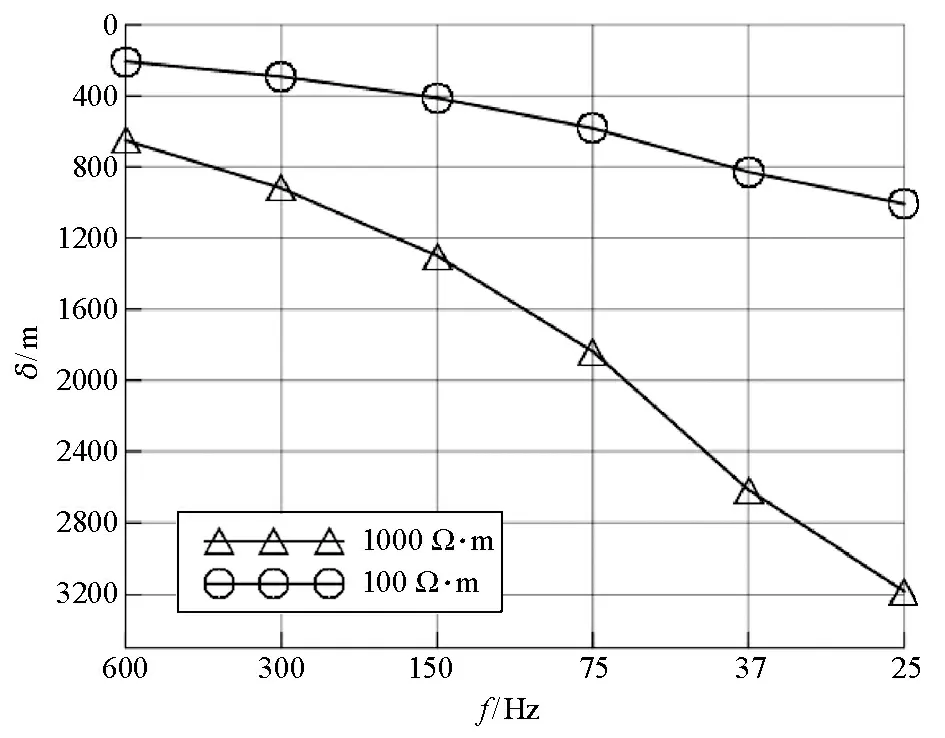
图2 频率-趋肤深度曲线Fig.2 Curve of frequency-skin depth
从图中可以看出,ZTEM系统6个频率的趋肤深度线性增加,即ZTEM所选用的6个探测频率使得6个频率的趋肤深度大致呈均匀等间距分布,这种分布形式利于后期数据成图与反演计算。
3 三维有限元算法
本文使用商用软件COMSOL Multiphysics进行正演模拟。该软件是基于三维有限元算法的多物理场模拟软件,使用AC/DC模块建立典型三维地质模型,对大地电磁响应进行模拟,分析倾子响应特征。
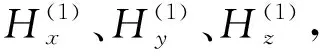
(4)
综合使用磁绝缘和理想磁导体边界条件,设置垂直场源的边界为理想磁导体边界,平行场源的边界为磁绝缘边界,从而达到模拟无限域的效果。使用自由四面体对模型进行网格剖分,对异常体网格加密,提高求解精度,模型剖分效果如图3所示。
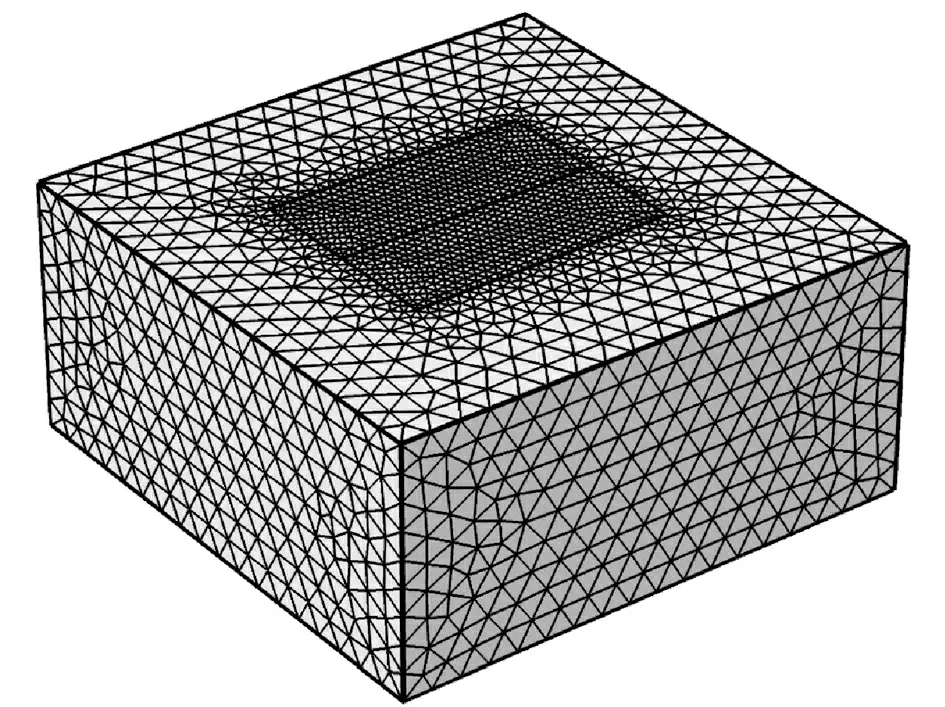
图3 模型网格剖分示例Fig.3 Example of model meshing
依据ZTEM系统所用频率,数值模拟中使用频率为25、37、75、150、300、600 Hz,模型背景电阻率100 Ω·m,充分考虑模拟边界效应以及最低频率最大探测深度应小于模型高度,设置模型长3 000 m,宽3 000 m,高1 400 m。为突出倾子对异常响应特点,异常体上方不设置覆盖层。
4 大地电磁三维正演模拟
4.1 全区域磁场三分量分布特征
航空大地电磁ZTEM系统数据采集过程中,基站固定于测区某个人文干扰低的地方采集磁场Hx、Hy分量,而不是沿测线进行数据采集。这种采集方式基于磁场Hx、Hy分量全区变化可忽略的假设,为验证上述假设,建立模型对大地电磁磁场三分量进行正演模拟,分析其分布特征。
如图4所示建立三维模型,模型长3 000 m,宽3 000 m,高1 400 m,背景电阻率为100 Ω·m,设置2个相同尺寸不同电阻率的异常体,单个异常体长1 500 m,宽600 m,高1 000 m,异常体电阻率值分别为10 Ω·m与1 000 Ω·m,选取沿红线方向的磁场三分量数据,进行成图分析。

图4 复杂地质模型示意Fig.4 Schematic diagram of complex geological modle
所选测线既有沿岩性分界面的情况,又有垂直岩性分界面的情况,相对具有代表性。选取37 Hz与300 Hz两个频率磁场三分量数据进行成图(图5),两幅图反映的规律类似:所选测线方向磁场水平分量Hx、Hy变化很小,基本可以忽略不计,磁场垂直分量Hz变化非常明显,在测线垂直相交的岩性分界面上出现极值点;由此验证了在实际数据采集过程中,测区固定地点采集Hx、Hy分量、沿测线采集Hz分量的采集方式的可行性。同时,从图中还可以看出2个频率出现极值点的位置相同,但极值绝对值大小不同,高频磁场Hz分量极值绝对值大于低频磁场Hz分量极值绝对值。
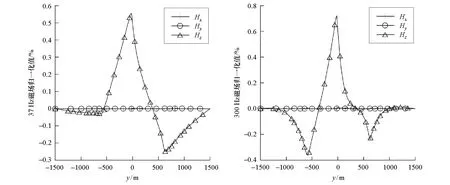
图5 2个典型频率的磁场三分量变化趋势Fig.5 Variation trend of three components of magnetic field at two typical frequencies
4.2 低阻体倾子响应特征
利用数值模拟对倾子响应特征进行分析的文章较多,所研究的响应特征皆为测线垂直岩性分界面的情况,但实际应用中测线设计不能每次都做到完全垂直岩性分界面。下面利用有限元法建立三维模型,研究测线与岩性分界面斜交时的倾子响应特征。
如图6所示,三维模型长3 000 m,宽3 000 m,高1 400 m,背景电阻率设为100 Ω·m;异常体长1 500 m,宽800 m,高1 000 m,异常体电阻率设为10 Ω·m,坐标原点为模型上表面中心点。利用三维有限元方法对大地电磁法进行数值模拟,研究倾子沿岩性分界面斜交测线低阻异常体的响应特征。
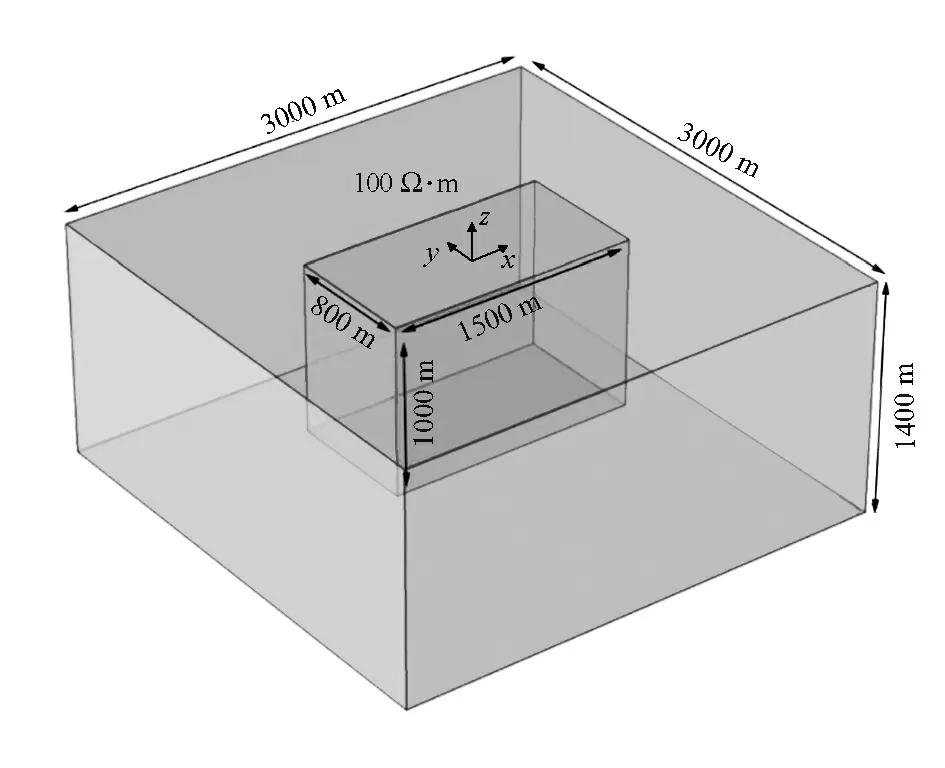
图6 三维模型示意Fig.6 3D model sketch
选择3条具有代表性的测线,如图7所示(图中为模型俯视图):测线a与x方向岩性分界面斜交;测线b过x方向和y方向岩性分界面交点,沿异常体对角线方向;测线c与y方向岩性分界面斜交。沿3条测线分别绘制6个频率的倾子Tx与倾子Ty曲线(图8~图10,图中虚线代表测线与岩性分界面相交位置),分析倾子响应特征。数值模拟和实际应用中倾子实部响应规律较倾子虚部响应规律好,文中所提倾子皆指倾子实部。
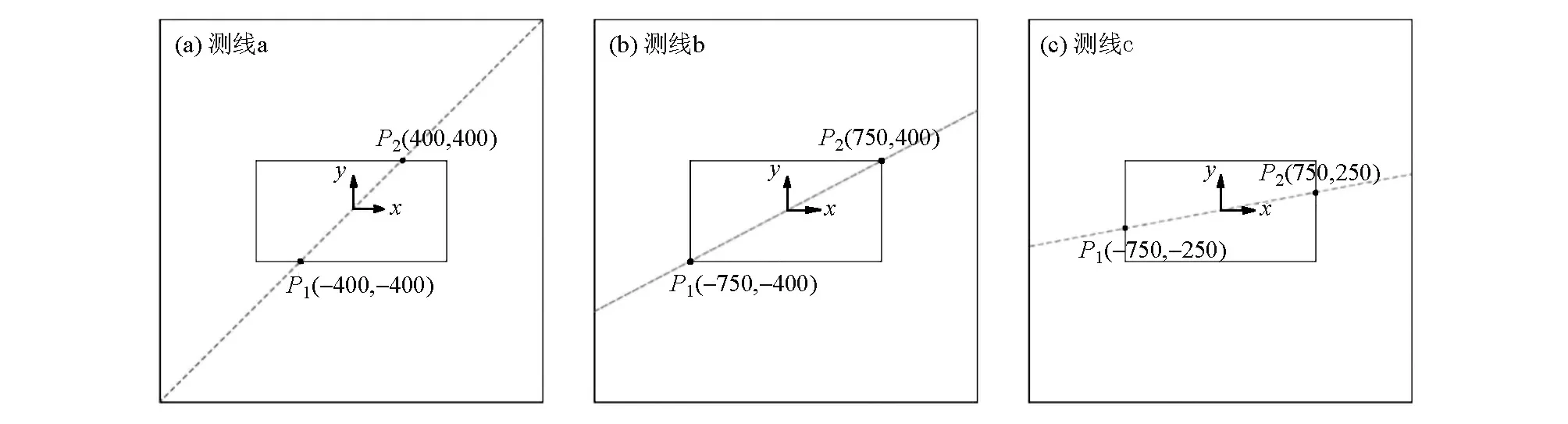
图7 测线走向示意Fig.7 Sketch map of survey line
图8为沿测线a倾子Tx与倾子Ty曲线,可以看出倾子Ty响应幅值高出倾子Tx响应幅值一个数量级,且倾子Ty响应极值点位置对岩性分界面位置显示较为准确。倾子Tx响应幅值较低,高频曲线对岩性分界面无反映,低频曲线对岩性分界面的响应特征与倾子Ty的响应特征类似,但曲线极值点与岩性分界面位置存在偏差,倾子响应极值点宽于岩性分界点。测线a沿y轴方向存在岩性变化,理论上表现为倾子Ty响应,由于测线非完全垂直于岩性分界面,存在微弱倾子Tx响应,该响应对岩性分界面的表现较差。
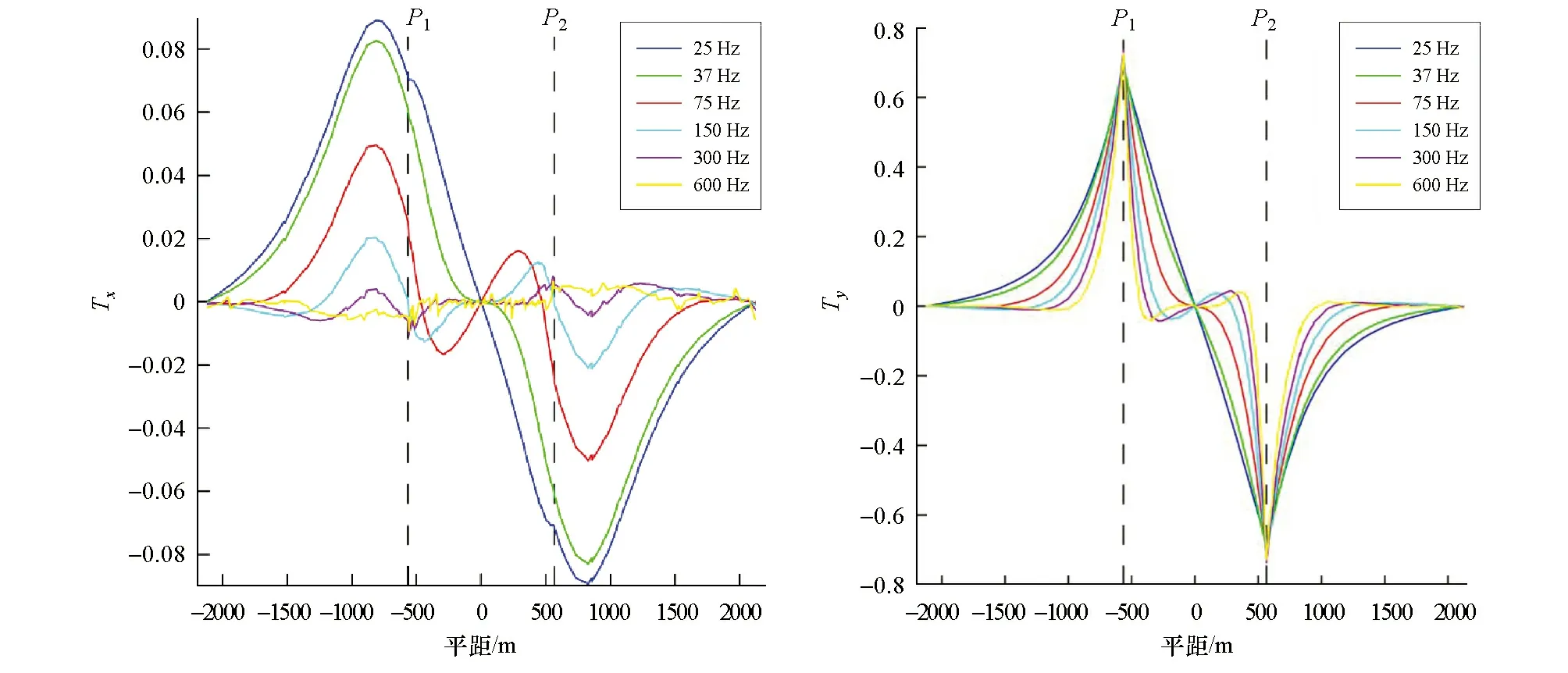
图8 测线a倾子低阻响应特征Fig.8 Low-resistance response characteristics of tipper on survey line a
图9显示,沿测线b倾子Tx响应幅值略低于倾子Ty响应幅值,各频率对于岩性分界面皆有响应,倾子Tx曲线极值点对岩性分界面的位置反映较为准确,但Ty曲线极值点对岩性分界面的位置反映存在偏差,曲线极值点范围窄于实际岩性分界面位置。
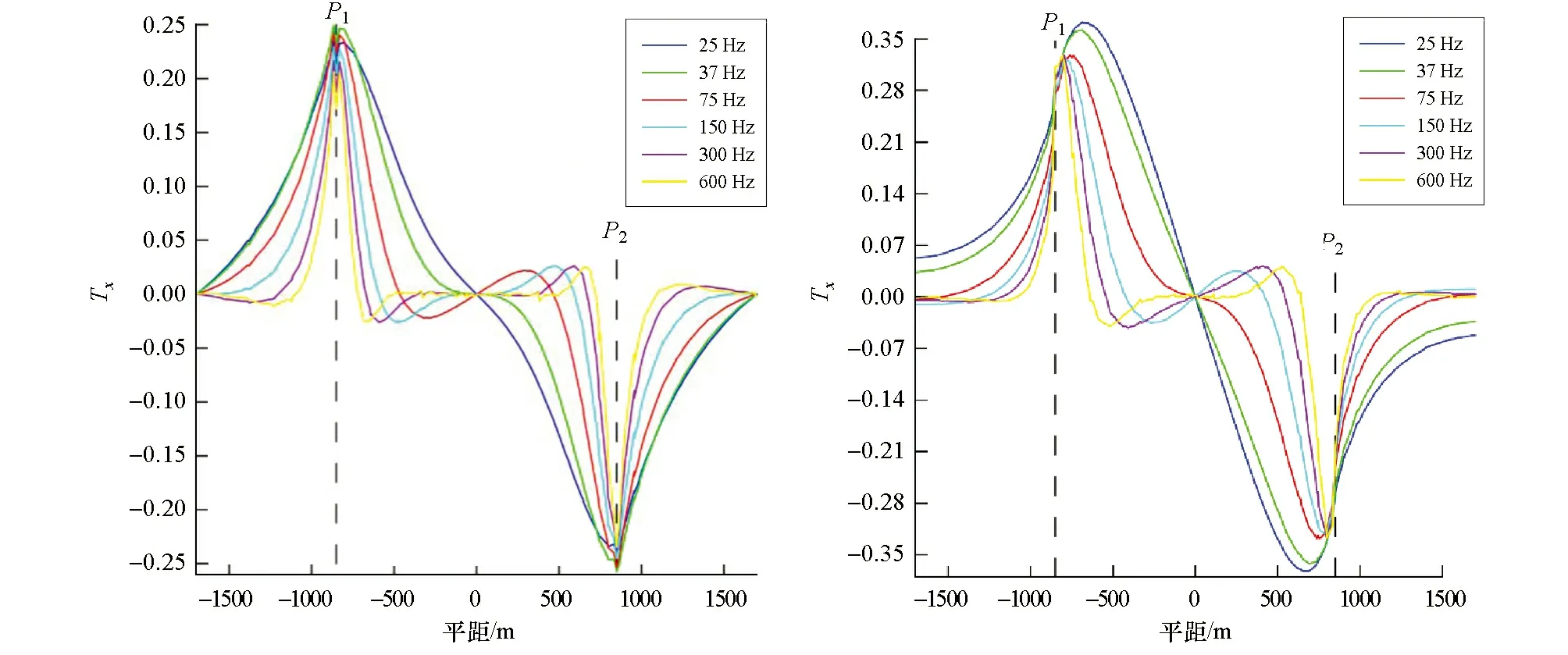
图9 测线b倾子低阻响应特征Fig.9 Low-resistance response characteristics of tipper on survey line b
图10显示,沿测线c倾子Tx响应幅值高于倾子Ty响应幅值,且前者曲线平滑度优于后者,倾子Tx对岩性分界面的位置反映较为准确。倾子Ty响应幅值较低,高频曲线对岩性分界面反映微弱,低频曲线极值点对岩性分界面位置反映存在偏差,曲线极值点反映的异常体宽度窄与实际异常体宽度。

图10 测线c倾子低阻响应特征Fig.10 Low-resistance response characteristics of tipper on survey line c
纵向对比图8、图9、图10,倾子Tx响应曲线反映x轴方向岩性变化,随着测线偏离x轴方向越大,倾子Tx响应幅值越低,对于岩性分界面的反映能力越差,曲线极值点过渡越平滑;而倾子Ty响应曲线反映y轴方向岩性变化,随着测线偏离y轴方向越大,倾子Ty响应幅值越低,对于岩性分界面的反映能力越差,曲线极值点过渡越平滑。
4.3 高阻体倾子响应特征
将图6模型异常体电阻率设置为1 000 Ω·m,模型背景围岩电阻率仍为100 Ω·m,坐标原点为模型上表面中心点。利用三维有限元方法对大地电磁法进行数值模拟,绘制沿图7测线倾子响应曲线,研究倾子沿岩性分界面斜交测线高阻异常体响应特征。
图11~图13分别对应3条测线倾子响应曲线。从图11可以看出,沿测线a倾子Tx响应幅值低于倾子Ty响应幅值,两者各个频率曲线极值对异常体边界皆有反映,倾子Tx极值点曲线过渡相对平滑,极值点位置与岩性分界点位置略微存在偏差,但偏差不大。图12表明,沿测线b倾子Tx响应与倾子Ty响应曲线类似且幅值相近,倾子Tx与倾子Ty曲线极值点对岩性分界面的位置反映皆较为准确。图13显示,沿测线c倾子Tx响应幅值高于倾子Ty响应幅值,倾子Tx与倾子Ty各频率曲线极值点对岩性分界面的位置反映皆较为准确。
对比图11、图12、图13可以看出,相同地质模型下,随测线偏离x轴方向越大,测线方向越接近y轴,倾子Tx响应幅值越低,倾子Ty响应幅值越高。对比低阻体响应曲线可以看出,高阻体倾子响应曲线较低阻体响应曲线光滑,响应幅值较低的测线上,倾子高频曲线不存在对异常体分界面无反映的状态。同时,对于低阻异常体,倾子曲线在岩性分界面形成极值,在异常体中段无岩性变化位置,倾子曲线存在值为零的水平段,如图10中倾子Tx响应,而高阻体模型中,倾子响应曲线在两极值间不存在倾子为零的水平段。实际上,在高阻异常体数值模拟中发现,只有当两边岩性分界面最够远时,倾子响应曲线才会在异常体中心位置出现倾子为零的水平段。
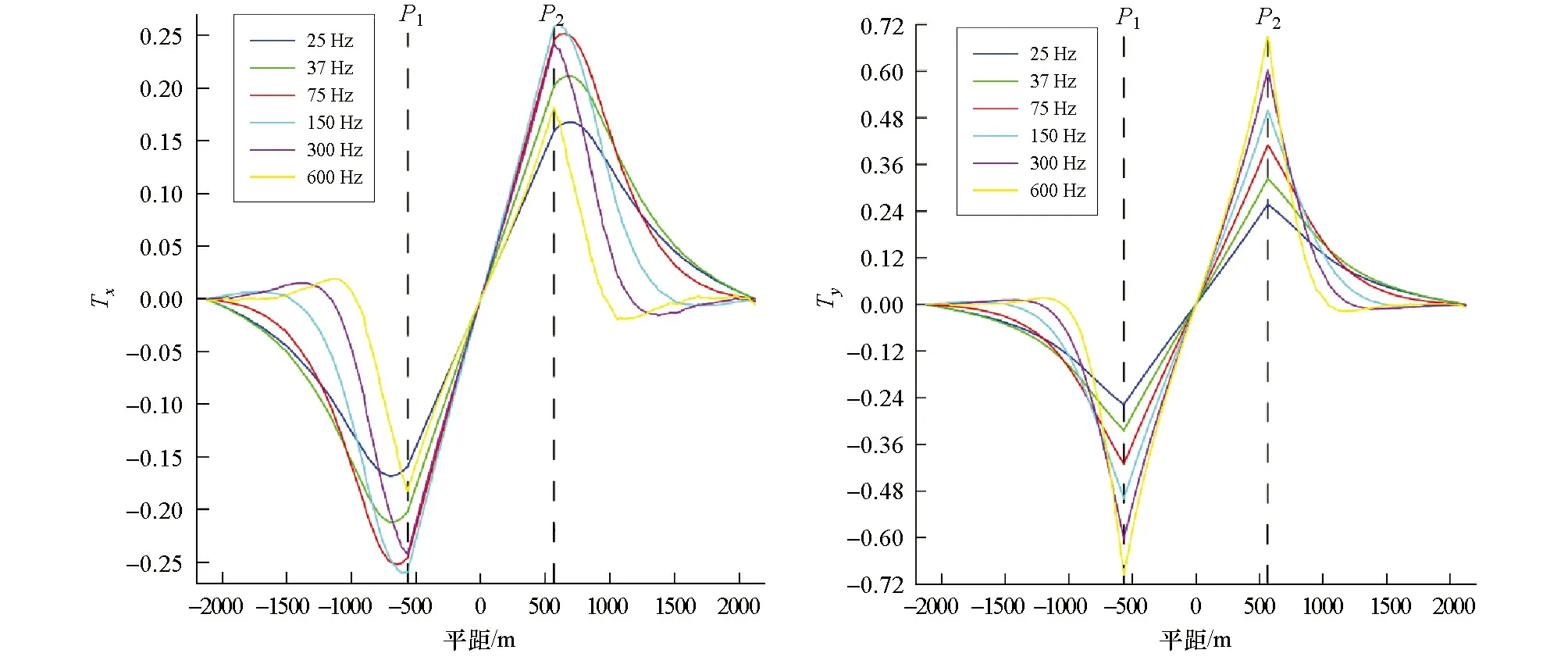
图11 测线a倾子高阻响应特征Fig.11 High-resistance response characteristics of tipper on survey line a

图12 测线b倾子高阻响应特征Fig.12 High-resistance response characteristics of tipper on survey line b
5 结论与讨论
1)航空大地电磁只采集磁场分量,在测区范围内磁场水平分量变化很小,只有地质体存在横向不均匀性时才能激发磁场垂直分量,所以航空大地电磁数据采集过程中,只需磁场垂直分量沿测线进行采集,水平分量固定地点测量即可。
2)倾子作为航空大地电磁数据解释中重要参数,在岩性横向分界面上表现为极值异常。当测线与岩性分界面斜交时,倾子Tx与倾子Ty对异常分界面皆有反映。随测线偏离x轴方向越大,测线方向越接近y轴,倾子Tx响应幅值越低,倾子Ty响应幅值越高,反之亦然。
3)倾子Tx对x轴方向岩性变化反映最好,当测线与x轴方向岩性变化分界面斜交时,倾子Ty对岩性分界面存在微弱反映,且当异常体为低阻体时,倾子Ty对岩性分界面位置反映存在偏差;同样,倾子Ty对y轴方向岩性变化反映最好,当测线与y轴方向岩性变化分界面斜交时,倾子Tx对岩性分界面存在微弱反映,且当异常体为低阻体时,倾子Tx对岩性分界面位置反映存在偏差。
4)相同地质模型,不同异常电阻率条件下,当测线与y轴方向岩性变化分界面斜交时,高阻异常体倾子Tx曲线较低阻异常体倾子Tx曲线平滑,且低阻异常体倾子Tx低频曲线对岩性分界面反映较差。
值得注意的是数值模拟为无噪声影响理想条件下的大地电磁响应特征,倾子曲线中高频响应幅值高于低频响应幅值,实际野外数据采集过程中,频率较高时,由于采样窗口窄,数据信噪较低。本文只讨论了倾子实部响应特征,可进一步对倾子虚部与相位响应特征进行研究,使用倾子多个参数对地质异常进行解释,提高航空大地电磁探测准确度。

