致密砂岩储层脆性测井评价方法研究及应用
——以鄂尔多斯盆地渭北油田为例
朱颜,韩向义,岳欣欣, 杨春峰,常文鑫,邢丽娟,廖晶
(中国石油化工股份有限公司 河南油田分公司勘探开发研究院,河南 郑州 450018)
0 引言
近年来,致密油、页岩油、页岩气等非常规油气勘探已成为国内外油气勘探的热点领域。鄂尔多斯盆地渭北油田三叠系延长组是主力含油层系,储层具有横向变化快、非均质性强、厚度薄等特点,属于典型的低孔、低渗、欠压式致密砂岩储层。常规技术难以开采,需要进行压裂才能得到有经济效益的油气[1-2]。脆性指数是评价致密油勘探“甜点”区的重要指标之一,也是致密砂岩储层压裂及射孔井段优选的重要依据[3-4],因此如何准确地预测脆性指数已成为渭北油田致密油高效勘探开发的重要难题之一。
中外学者对致密砂岩储层脆性评价开展了大量的研究,Obert将脆性定义为材料需要很小外力就破裂或断裂的性质,在致密砂岩储层评价中,主要通过岩石脆性表征岩石压裂的难易程度[5-6];黄军平等提出了基于多元回归的致密砂岩储层脆性评价方法[7];任岩等基于吉木萨尔致密油储层提出了基于改进矿物组分的致密油储层脆性预测方法[8];张平等基于岩石物理实验提出了致密油储层脆性预测方法[9]。调研发现目前还没有专门针对致密砂岩储层脆性指数的预测方法,主要借鉴的还是页岩的脆性指数预测方法,即岩石矿物组分法和岩石弹性参数法[10-12]。其中岩石矿物组分法是利用录井资料获取岩石不同矿物的弹塑性,直接求取纵向上的岩石脆性指数,难以获得其横向展布规律;而弹性参数法可以根据测井资料,利用归一化的杨氏模量、泊松比求取脆性指数,进而通过弹性参数反演获取脆性的横向展布规律[13]。但是实际生产中偶极子声波测井成本太高,生产资料中往往缺少横波速度,横波测井资料的匮乏严重制约了弹性参数的计算[14]。
国内外学者也对横波速度预测开展了大量的研究, Castagna等基于碎屑岩中的纵、横波速度之间的关系,提出了著名的“泥岩线”公式[15];Xu和White提出了基于砂泥岩孔隙的砂泥岩等效介质模型“Xu-White 模型”,较为精确地进行了横波速度的预测[16];Pride和Lee提出了P-L 模型,基于岩石物理建模进行横波速度的预测[17];Xu 和Payne通过估算碳酸盐岩的孔隙形状,预测了碳酸盐岩的横波速度[18];李成文等提出了基于密度、伽马、电阻率等测井参数多元回归的横波预测方法[19]。传统的岩石物理手段预测横波速度是针对于常规碎屑岩、碳酸盐岩地层提出的,对于低孔、低渗的致密储层不一定适用或预测误差较大,而且其算法极其复杂,所需参数多,有些参数难以获得,导致计算效率很低[20-21]。随着计算机的发展,机器学习在勘探领域取得了巨大的突破,ANN是基于回归思想的一种深度学习方法,已广泛应用于在其他领域序数列的分析和预测,本次研究主要采用ANN模型进行横波预测,主要包括神经网络构建、数据预处理、样本训练和数据预测,通过已知井的验证发现预测值与实测结果高度吻合,进而进行脆性指数预测,为了保障预测的准确性,笔者又利用研究区矿物组分法预测脆性指数对弹性参数法进行了校正。在此基础上开展了渭北油田WB2井区致密砂岩储层测井脆性评价,为有利目的层段压裂提供了依据。
1 ANN横波预测技术原理
1.1 ANN技术原理
人工神经网络(artificial neural network,ANN)是计算机领域用于处理机器学习问题的强大工具,其广泛应用于回归与分类等问题中,由大量被称为神经元的简单处理单元组成,通过模仿人类大脑的行为而发展。和人类大脑一样,神经网络通过“学习过程”从环境中收集信息,将一个个具有层次关系、连接关系的人工神经元组成网络结构,通过数学表达的方式模拟神经元之间的信号传递,从而可建立一个具有输入与输出关系,并可通过网络方式建立可视化的非线性方程,称之为ANN。一般而言,ANN可以通过合理的网络结构配置拟合任意非线性函数,因此它也用于处理内部表达较为复杂的非线性系统或黑箱模型。其网络结构如图1所示[22-24]。
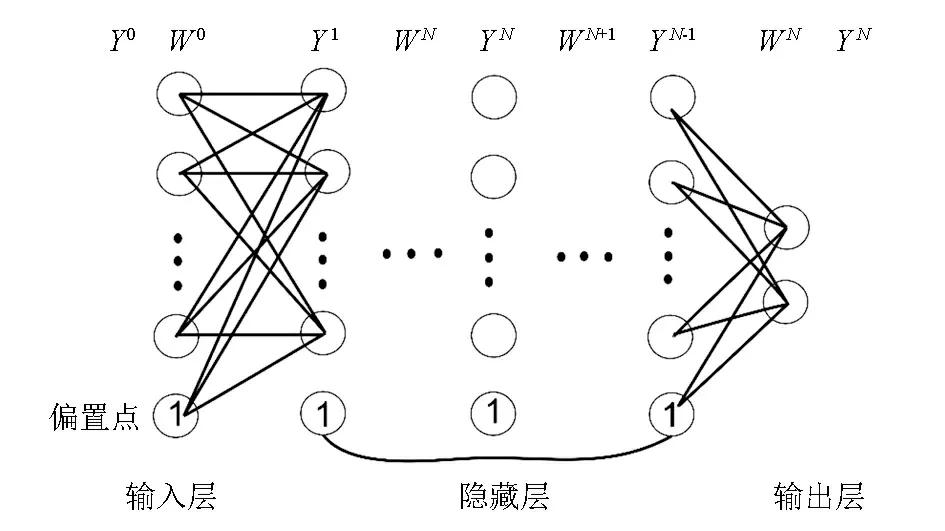
图1 人工神经网络结构Fig.1 Structure diagram of artificial neural network
假设神经网络的层数为N层(N>1),输入层到输出层各层节点个数(不包含偏置节点1)分别为k1,k2,…,kN,由此定义了输入向量的维度为k0,输出向量的维度为kN。网络的每一层输出向量YN分别表述如下:
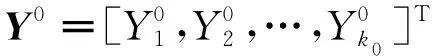



因为每个神经元的权重不同,因此还需要每个元素对输入层的偏置向量的加权和,将其定义为NETN,其表达式为:
(1)
式中:WN权重矩阵;bN为偏置向量。通过正向逐层计算,可得到网络中每一层的NETN与YN,及每层的输入向量与输出向量,从而也就得到了每个神经元的输入值和输出值。ANN横波预测技术是选取资料较全而真实的测井数据,作为样本井进行学习训练,以与横波有一定相关性或存在一定地质意义的敏感性曲线为输入,通过网络的学习训练,逐步修正自己的各连接的权重即偏置向量的加权和,使网络的输出逐渐逼近固有真实值。
1.2 基于ANN的横波速度预测方法
基于ANN横波预测方法流程如图2所示,其主要包括输入层、隐蔽层和输出层。输入层对与横波测井数据有一定相关性的测井参数进行异常值处理和归一化处理(归一化能够提高神经网络训练的速度和精度)。其归一化公式为:
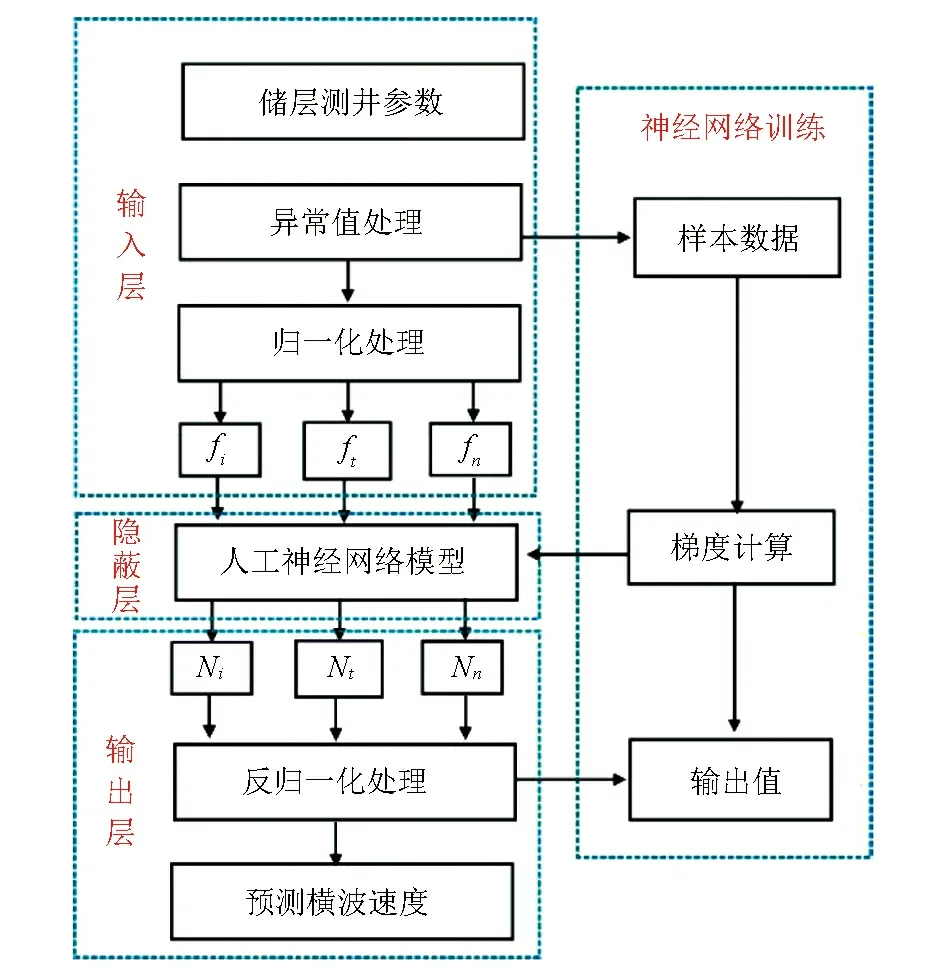
图2 ANN横波速度预测方法流程Fig.2 Flow chart of ANN shear wave velocity prediction method
fi=(fi-fmin)/(fmax-fmin) ,
(i=1,2,…,n) ,
(2)
式中:fmin和fmax为fi的最小值和最大值。将处理后的数据输入到隐蔽层,隐蔽层接收数据并利用神经网络模型进行计算,然后将计算结果传递给输出层,输出层接收计算结果并进行反归一化处理,最终提供预测横波速度信息。在神经网络模型进行训练时,利用随机梯度下降法计算各自的权重值和偏置向量的加权和,这种方法不但提高了计算效率,而且保证了横波速度预测的精度。本次研究选取了工区测井资料全且有横波测井数据的3口井进行测井数据分析,通过交会分析,发现横波测井数据与纵波速度、自然伽马、孔隙度存在一定的关系如图3所示,因此本次样本选取了纵波速度、自然伽马、孔隙度作为横波速度的输入,逐步修正它们各连接的权重,通过神经网络训练逼近它们与横波速度之间的关系,从而将逼近真实的横波速度预测值作为输出。

图3 研究区测井曲线与横波时差交会Fig.3 Intersection of well logging curves and shear wave velocity in the study area
本次研究共选取了工区8口井进行横波速度预测,8口井都包含纵波时差、密度、自然伽马、孔隙度、电阻率等,其中3口井目的层段有横波测井资料,利用这3口有横波资料的井作为样本井来构建神经网络模型,通过神经网络训练得到最逼近实测横波速度的预测模型。图4所示是训练井预测横波速度与实测横波速度对比,由图可见,预测的横波速度与实际的横波速度吻合度高,说明预测结果可靠。

图4 不同井横波速度预测值与实测真实值对比Fig.4 Comparison of predicted values of S-wave velocity and actual measured values with different wells
最后将5口没有横波曲线井的纵波速度、孔隙度、自然伽马作为输入到已经训练好的神经网络模型之中,通过神经网络预测得到每口井的横波曲线。如图5所示是WB48井预测的横波曲线,根据岩相可以看出在砂岩段横波速度高,在油页岩和泥岩段速度较小,符合一般地质规律,说明预测可靠。

图5 WB48井目的层段横波速度结果分析Fig.5 Analysis results of shear wave velocity in the target interval of WB48 well
因此我们认为根据横波速度与纵波速度、孔隙度、自然伽马等参数之间的相关性,所采用的ANN横波预测方法在研究区预测横波速度相对误差较低,可以应用其进行下一步的脆性预测等工作。
2 致密砂岩储层测井脆性评价
致密砂岩脆性预测主要借鉴页岩脆性预测方法,即基于实验室矿物组分分析法和弹性参数计算法,研究区由于实验室化验分析资料不足,只有少量的分析化验资料,因此本次研究主要基于上面预测的横波速度来间接利用弹性参数法计算脆性,为了减小误差,我们用矿物组分法对弹性参数法进行了校正,提出了一种适用于研究区致密砂岩储层的测井脆性评价方法。
2.1 矿物组分对岩石脆性评价
分析研究区WB48井全岩矿物X衍射数据(表1),结果表明:延长组各层段岩石矿物组分变化较小,主要包含石英、长石和岩屑,其中岩屑以沉积岩岩屑为主,填隙物主要是方解石和白云石碳酸盐岩类矿物以及高岭石、绿泥石和伊利石等黏土类矿物。其中石英、长石、碳酸盐岩类矿物含量的分别介于26%~55%、26%~47%和2%~25%。

表1 WB48井延长组全岩矿物X衍射数据
一般岩石力学认为,杨氏模量表示岩石的刚性,杨氏模量越大说明它越不易于发生形变,脆性就越大。泊松比反映岩石抵抗破裂能力,泊松比越小,岩石越容易裂开。所以总体来说杨氏模量越高、泊松比越低,则脆性指数越高[25]。我们对石英、长石、碳酸盐岩类矿物和黏土类矿物与杨氏模量、泊松比进行了交会分析(图6)。如图6a所示石英随杨氏模量的增大而增大,随泊松比减小而减小,因此石英为脆性矿物;长石是否为脆性矿物,不同学者看法不一,徐蕾等[26]从晶体光学角度对长石组矿物的脆性差异进行了分析,认为钙长石脆性较强,钠长石和钾长石脆性较弱,通过对渭北地区延长组矿物成分化验分析,其长石主要为钠长石和钾长石,未见到钙长石,且从交会图6b可以看出长石与弹性参数没有明显关系,因此认为在渭北地区脆性计算中长石作为非脆性矿物处理;如图6c所示碳酸盐岩类矿物随杨氏模量增大而增大,随泊松比减小而减小,碳酸盐岩类矿物在渭北地区属于脆性矿物;如图6d所示黏土类矿物随杨氏模量增大而减小,随泊松比增大而增大与脆性成负相关。综上,分析判定研究区主要脆性矿物为石英和碳酸盐岩类矿物,可以利用其矿物组分来计算岩石脆性指数,表达式为:
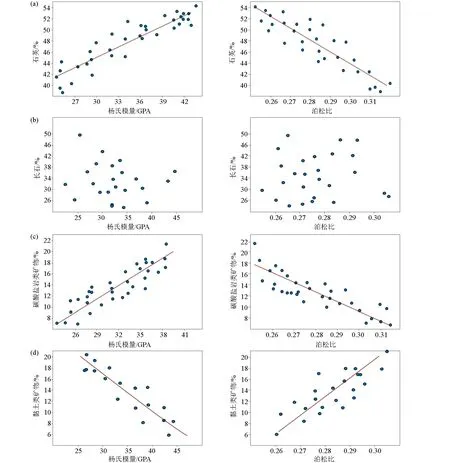
a—石英与杨氏模量、泊松比交会分析;b—长石与杨氏模量、泊松比交会分析;c—碳酸盐岩类矿物与杨氏模量、泊松比交会分析;d—黏土类矿物与杨氏模量、泊松比交会分析a—intersection analysis of quartz with Young's modulus and Poisson's ratio;b—intersection analysis of feldspar with Young's modulus and Poisson's ratio;c—intersection analysis of carbonate with Young's modulus and Poisson's ratio;d—intersection analysis of clay minerals with Young's modulus and Poisson's ratio图6 石英、长石、碳酸盐岩类矿物和黏土类矿物与杨氏模量、泊松比交会分析Fig.6 Intersection analysis of quartz,feldspar,carbonate and clay minerals with Young's modulus and Poisson's ratio
(3)
式中:mBi为矿物组分计算脆性指数;ωQu为石英矿物含量;ωCa为碳酸盐岩类矿物含量;ωFe为长石矿物含量;ωCl为黏土类矿物含量。通过公式可以获取样本点各采样点的脆性值。
2.2 基于弹性参数计算的储层脆性预测
基于前面ANN预测的纵、横波速度,计算出杨氏模量和泊松比:
(4)
(5)
式中:E为杨氏模量,σ为泊松比,Vp为纵波速度,Vs表示横波速度,ρ为密度。
根据Rickman等[27]提出的利用归一化的杨氏模量、泊松比、岩石力学参数计算脆性指数:
E=(YMS_C-YMSmin)/(YMSmax-YMSmin)×100 ,
(6)
σ=(PR_C-PRmax)/(PRmin-PRmax)×100 ,(7)
BI=(E+σ)/2 ,
(8)
式中:YMS_C为计算的杨氏模量;YMSmax为杨氏模量最大值;YMSmin杨氏模量最小值;PR_C为计算的泊松比,PRmax为泊松比最大值,PRmin为泊松比最小值;BI为弹性参数计算脆性指数。
通常情况下用计算获取的杨氏模量、泊松比最大值最小值直接代入式(6)、(7)、(8)计算脆性指数,但是计算结果发现与矿物组分法计算结果(式(3)中计算)存在一定误差,因此需要利用矿物组分所获取脆性指数来校正弹性参数计算的脆性指数。具体做法是首先建立计算杨氏模量与计算泊松比的交会图版如图7,定义一个区域韧度值和区域刚度值,区域韧度值表征塑性,即低杨氏模量、高泊松比,区域刚度值表征脆性,即高杨氏模量、低泊松比,然后通过在交会图版上移动选择适当的区域韧度值和区域刚度值,也就是寻找区域上杨氏模量、泊松比的最大和最小值点,交互式调节图7、图8,通过不断的实验选点直到弹性参数计算脆性指数(图8中红色曲线)与矿物组分计算脆性指数高度吻合时,作为校正后的区域韧度值和区域刚度值如图7,当选取区域上泊松比最小值0.11,最大值0.36,杨氏模量最小值10 GPA,最大值66 GPA时,弹性参数与矿物组分所计算的脆性指数最吻合(图8)。

图7 杨氏模量、泊松比交会图版Fig.7 Intersection diagram of Young’s modulus and Poisson’s ratio

图8 渭北地区致密油井脆性指数预测Fig.8 Prediction of brittleness index of tight oil wells in Weibei area
图8中黑点为矿物组分计算获取的脆性指数,红色的曲线为弹性参数计算获得。最终寻找到了适合研究区的计算参数和校正方法,建立了储层的脆性指数评价模型。
3 应用效果
根据鄂尔多斯盆地渭北油田致密油井的测井资料,利用ANN横波预测方法预测获得横波测井资料,基于本文方法进行致密砂岩储层脆性测井评价,计算研究区WB52井、WB48井的脆性指数,如图9所示,该计算方法可以有效反映储层纵向剖面上岩石的脆性指数差异。

图9 渭北地区致密油井脆性预测结果Fig.9 Brittleness prediction results of tight oil wells in Weibei area
结果显示,WB52井在C8段1 095~1 105 m砂岩段有较好的油侵显示,在1 095~1 099 m(红色框上部)测井脆性指数评价脆性指数较低,测井解释为二类“甜点”储层,在1 100~1 106 m(图中红色框内)脆性指数较高,结合测井曲线解释为一类“甜点”储层。对该井C8段1 098~1 105 m段射孔并压裂后日产油3.5 t产能较好。WB48井C6段805~820 m砂岩段钻遇良好油迹显示,根据测井储层脆性预测结果在805~810 m(红色框上部)脆性指数较低,测井解释为二类储层压裂后并无产能,在814~818 m高脆性段(图中红色框内)测井解释属于一类储层进行压裂改造,压裂后日产油2.5 t。因此本文方法在缺乏横波测井资料的情况下,基于ANN进行横波预测,进而通过弹性参数计算脆性,利用矿物组分计算的脆性指数来校正弹性参数计算的脆性指数,其计算精度较高,可以为研究区有利层段压裂改造提供依据,为研究区增储上产做出了贡献。
4 结论
致密砂岩储层的岩性组合、岩石矿物组分非常复杂,常规基于碎屑岩、碳酸盐岩地层提出的传统的岩石物理手段,预测致密砂岩储层横波速度的适用性差且计算效率低,本文提出的基于人工神经网络模型的横波预测技术方法,主要依赖于机器学习,计算效率高且预测值与实测值吻合度高,能够有效解决研究区横波资料匮乏的实际问题。
对于致密砂岩储层脆性预测,单一的弹性参数法或矿物组分法计算脆性指数误差较大,不能很好地指示地层压裂的有利层段。利用弹性参数计算脆性指数,通过矿物组分计算的脆性指数对弹性参数法计算脆性指数进行校正,可以获得最逼近实际的脆性指数。将该方法应用于渭北油田致密砂岩储层测井评价,为研究区有利层段压裂选择提供了指导。
渭北地区致密砂岩脆性测井评价方法的成功应用,为致密砂岩有利压裂层段选取提供了依据,也为其他类似地区致密砂岩储层脆性预测提供了借鉴。在应用时,一方面要注意ANN横波预测时要合理地优选敏感性参数建立ANN模型;另一方面要根据不同地区准确地优选矿物组分计算脆性的计算公式。

