弹簧改进型双凹面摩擦摆隔震支座理论分析与数值模拟研究*

谢黄东，陶 忠，张龙飞，赵李俊，刘海龙

(1.昆明理工大学建筑工程学院，云南 昆明 650051； 2.云南省工程抗震研究所，云南 昆明 650500；3.昆明学院建筑工程学院，云南 昆明 650214； 4.林同棪国际工程咨询(中国)有限公司，重庆 401121；5.兰州理工大学土木工程学院，甘肃 兰州 730050)

0 引言

自20世纪80年代Zayas等[1]研发了摩擦摆隔震支座以来，众多学者对该支座进行了研究，其中Mokha等和Constantinou等[2-4]的研究表明，摩擦摆隔震支座滑道设置聚四氟乙烯时，静摩擦系数大于动摩擦系数，且摩擦系数与接触面摩擦材料、分布在接触面的压强等有关；Mokha等[5]开展了摩擦摆隔震支座在近断层地震作用下的快速滑动与抗拉性能试验研究；Pranesh等[6]研发了变频摆隔震支座，可弥补普通摩擦摆隔震支座部分缺陷；Tsai等[7-9]陆续提出了变曲率摩擦摆、沟槽摩擦摆、方向优化摩擦摆隔震支座，并进行了理论分析、数值模拟及试验研究；Morgan等[10]提出了多级摩擦摆隔震支座，并进行了试验与数值模拟研究；Kol等[11]通过理论分析与数值模拟研究了变摩擦-摩擦摆隔震支座减震机理及减震效果；钱由胜等[12]通过有限元分析研究了FPB摩擦系数对隔震桥梁的影响；邓雪松等[13-16]通过理论分析与有限元数值模拟，对普通摩擦摆、双凹面摩擦摆、变曲率摩擦摆及变曲率摩擦复摆隔震支座进行了研究，分析了支座滞回特性与恢复力特性；陈伟等[17]通过概率分布参数估计方法，研究了摩擦摆隔震支座等效黏滞阻尼比取值；王乔炎等[18]研究了普通摩擦摆隔震支座在不同矢跨比柱支承单层球面网壳结构的力学性能。由于普通摩擦摆、双凹面摩擦摆隔震支座无法控制提离情况，利用弹簧改进后，可减小提离量，且可提供一定防倾覆能力，因此，本文提出弹簧改进型双凹面摩擦摆隔震支座(spring-double concave friction pendulum bearing, S-DCFPB)，进行理论分析与数值模拟研究。

1 理论分析

1.1 基本构造

S-DCFPB由上支承板、下支承板、摩擦材料层(聚四氟乙烯涂层)、上滑动块、下滑动块、弹簧组成，聚四氟乙烯涂抹于上、下支承板滑动面内，弹簧设置在上下支承板角部，如图1所示。

图1 S-DCFPB构造示意

1.2 工作原理

S-DCFPB工作原理为：当地震来临时，通过克服静摩擦力发生滑动，使上部结构与基础隔开，并延长结构周期，进而避免共振；克服静摩擦力后，弹簧开始工作，将地震能量转换为一部分弹簧应变能，弹簧提供的竖向分力可减小上部结构提离量，使结构具有一定防倾覆能力；地震结束后，在弹簧水平分力和结构自重共同作用下产生恢复力。

1.3 刚度与周期

对地震作用下下支承板受力进行分析(见图2)，由力学平衡原理可得：

图2 下支承板受力示意

N-4Fscos(θ1+θ)-Wcosθ1-Fsinθ1=0

(1)

T+4Fssin(θ1+θ)+Wsinθ1-Fcosθ1=0

(2)

式中：N为下滑动块作用在下支承板滑动面的法线方向压力；Fs为弹簧弹力；θ1为下滑动块相对于滑动凹面中心的旋转角；θ为弹簧与竖直方向的夹角；W为下部结构对下支承板的作用力；F为下支承板受到的水平剪力；T为下支承板滑动面受到的切线方向摩擦力。

由式(2)可得：

(3)

将式(3)代入式(1)可得：

N=Wsecθ1+4Fscosθsecθ1+Ttanθ1

(4)

由库仑摩擦定律可得：

(5)

将式(5)代入式(3)可得：

(6)

由Fs定义可知：

Fs=ksΔ，

(7)

式中：ks为弹簧刚度；Δ为弹簧伸长量；x为支座滑移量；h为弹簧初始长度。

下支承板受到的水平剪力可视为恢复力、摩擦力和水平方向弹簧弹力的和，且μtanθ1≈tan2θ1≈0，式(6)可简化为：

(8)

下支承板水平剪力简化为：

(9)

由于上、下支承板滑动面均为球面，所以有：

(10)

进而得到隔震支座水平剪力为：

(11)

隔震支座刚度kr表达式为：

(12)

隔震支座周期T表达式为：

(13)

1.4 恢复力特性

当隔震支座自动恢复时，应满足：

(14)

即：

(W+4ksΔcosθ)tanθ1+8ksΔsinθ≥

(15)

残余位移表达式为：

(16)

2 数值模拟研究

2.1 模型建立

采用有限元软件ABAQUS建立S-DCFPB和双凹面摩擦摆隔震支座(double concave friction pendulum bearing，DCFPB)模型(见图3)，在DCFPB上、下支承板四角采用弹簧连接即为S-DCFPB。对S-DCFPB在低周往复荷载作用下的滞回性能与设计位移下的恢复能力，并验证理论公式正确性。由于重点研究S-DCFPB滑移滞回性能，故将支座控制为弹性受力状态，设定摩擦系数，并采用八结点线性六面体减缩积分单元(C3D8R)划分网格。

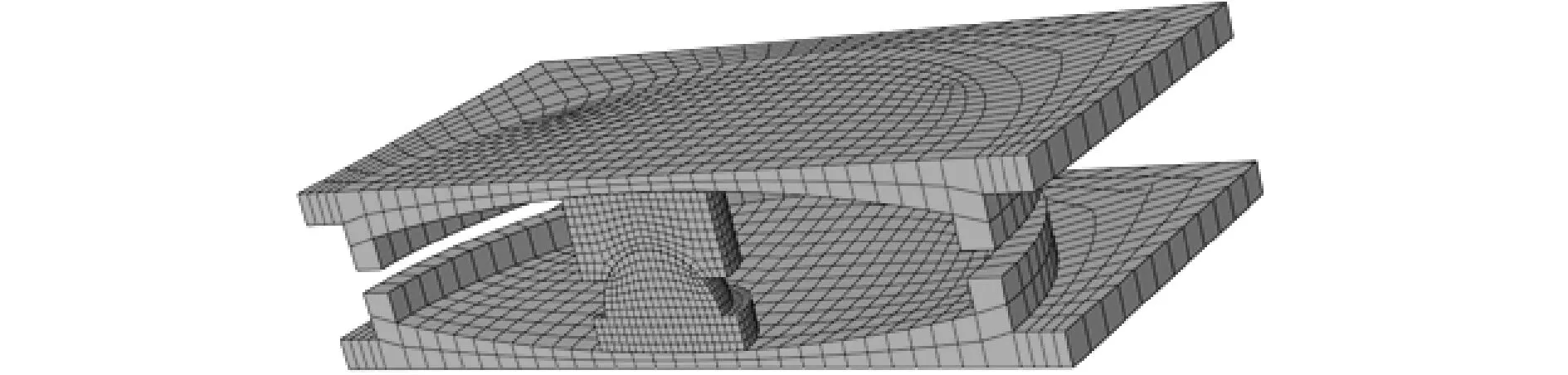
图3 有限元模型

上、下滑动面及上、下球铰面均设有接触对，接触面切线方向采用“表面-表面接触”，法线方向采用“硬接触”，加载过程中，竖向荷载(下部结构对下支承板的作用力)始终取为500kN，水平荷载采用控制位移的变幅等幅混合加载制度，位移峰值取为100，200mm，加载历程如图4所示。

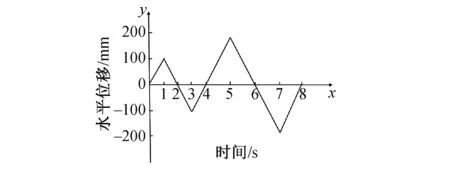
图4 水平荷载加载历程

2.2 滞回特性

将S-DCFPB曲率半径取为1m，最大滑移量取为200mm，摩擦系数取为0.3，弹簧刚度取为150kN/m，得到S-DCFPB滞回曲线如图5所示。由图5可知，滞回曲线饱满且对称，表明S-DCFPB具有良好的耗能能力；S-DCFPB可提供非线性恢复力及非线性刚度；理论计算与数值模拟结果吻合度较高。

图5 S-DCFPB滞回曲线

将S-DCFPB，DCFPB曲率半径均取为1m，最大滑移量均取为200mm，摩擦系数均取为0.3，并将S-DCFPB弹簧刚度取为150kN/m，得到S-DCFPB，DCFPB滞回曲线如图6所示。由图6可知，在曲率半径、最大滑移量、摩擦系数相同的情况下，加载位移较小时，支座提供的恢复力较小；随着位移的增大，支座提供的恢复力增大。

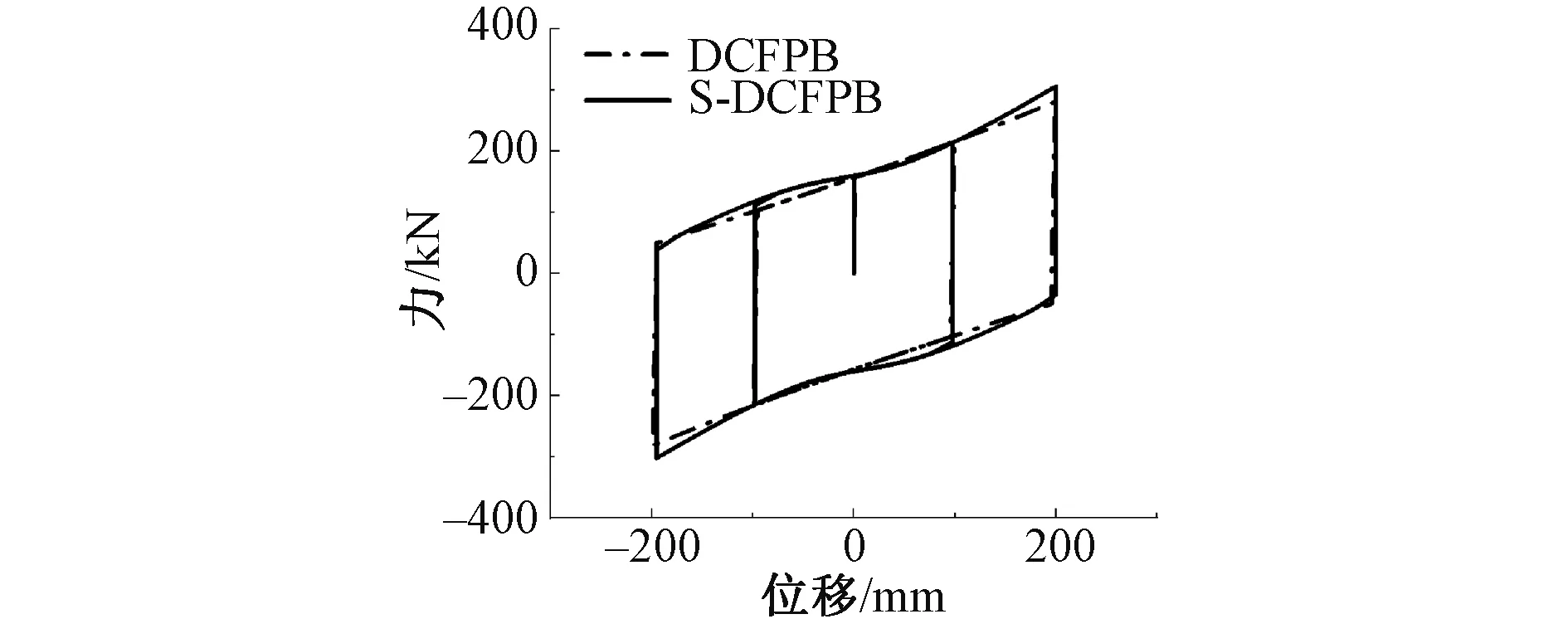
图6 S-DCFPB，DCFPB滞回曲线

将S-DCFPB曲率半径均取为1m，最大滑移量均取为200mm，摩擦系数均取为0.1，弹簧刚度分别取为100，150，200kN/m，得到不同弹簧刚度下S-DCFPB滞回曲线如图7所示。由图7可知，弹簧刚度越大，弹簧提供的恢复力越大，S-DCFPB刚度越大，但耗能效果会降低。因此，弹簧刚度应设置在合理范围内，以免降低隔震支座减隔震效果。

图7 不同弹簧刚度下S-DCFPB滞回曲线

将S-DCFPB曲率半径均取为1m，最大滑移量均取为200mm，弹簧刚度均取为100kN/m，摩擦系数分别取为0.06，0.1，0.3，得到不同摩擦系数下S-DCFPB滞回曲线如图8所示。由图8可知，摩擦系数越大，滞回环面积越大，S-DCFPB耗能能力越强。随着摩擦系数的增加，支座恢复能力变差，应将摩擦系数设置在合理范围内。

图8 不同摩擦系数下S-DCFPB滞回曲线

2.3 残余位移

当摩擦系数取为0.03时，S-DCFPB，DCFPB最大残余位移分别为50.7，60.5mm；当摩擦系数取为0.1时，S-DCFPB，DCFPB最大残余位移分别为125.2，195mm。对比可知，S-DCFPB最大残余位移小于DCFPB，同样表明S-DCFPB恢复力特性较好。

2.4 等效黏滞阻尼比与耗能系数

当曲率半径取为1m、摩擦系数取为0.3时，计算得到S-DCFPB，DCFPB等效黏滞阻尼比分别为0.36，0.45，耗能系数分别为2.26，2.86，可知S-DCFPB耗能能力虽较DCFPB有所降低，但整体耗能能力较好。

2.5 应力

为保证支座发挥减隔震作用并正常工作，对S-DCFPB应力进行分析，结果如图9所示。由图9可知，反向加载至左侧、正向加载至右侧S-DCFPB最大应力分别为133.5，144.5MPa，受挤压作用，最大应力出现在球铰面挤压处，设计时应选择合适的球铰面尺寸。为保证支座正常工作，需使支座保持弹性状态。

图9 S-DCFPB应力云图(单位：MPa)

3 结语

提出弹簧改进型双凹面摩擦摆隔震支座，并对其进行理论分析与数值模拟研究，得出以下结论。

1)S-DCFPB理论计算与数值模拟滞回曲线吻合较好，可知本文推导的理论公式较合理。

2)S-DCFPB滞回曲线饱满且对称，表明其具有良好的耗能能力，可提供非线性刚度。

3)S-DCFPB弹簧刚度、摩擦系数应设置在合理范围内，以免降低隔震支座减隔震效果。

4)S-DCFPB最大残余位移较小，恢复力特性较好。

5)S-DCFPB最大应力出现在球铰面挤压处，设计时应选择合适的球铰面尺寸。为保证支座正常工作，需使支座保持弹性状态。