青龙水库沥青混凝土心墙堆石坝坝料分区优化与静动力分析

吴 涛

(四川大学工程设计研究院有限公司，四川 成都 610065)

土石坝作为历史悠久的一种坝型，对地质条件适应能力强，筑坝材料可充分利用当地材料和建筑物开挖料，具有较好的经济效益，广泛运用于水利工程的生产实践之中。土石坝又称作当地材料坝，其筑坝材料和防渗材料决定了坝型方案，沥青混凝土心墙堆石坝即是广泛运用于四川红层地区的一种当地材料坝型，该坝型不需专门开采防渗料，同时可将硬质岩堆石料和较硬岩石渣料分区上坝利用，既解决了四川山区黏土防渗料难以获得、集中开采对生态环境破坏大等问题，又改善了黏土和泥岩等防渗料因施工不当而造成大坝防渗抗渗不可靠的情况，具有较大的优势。但由于该坝型的筑坝堆石料和石渣料变形存在差异，不合理的分区布置使坝体变形不协调，直接影响到心墙的安全；同时，堆石料相对石渣料开采难度大，材料单价高，堆石料用量直接影响坝体工程的经济指标。因此，在不增加堆石用量的基础上开展堆石料和石渣料的分区优化研究以提高混凝土心墙堆石坝的心墙安全性，具有一定的工程应用价值

1 工程概况

青龙水库地处乐山市马边县境内劳动乡的柏香村，工程建设任务是农业灌溉和农村供水等综合利用，兼为县城的应急备用水源。青龙水库为小(1)型水利工程，总库容105万m3，枢纽在主河槽布置大坝，在大坝右岸山体内布置导流兼取水(放空)洞，在大坝右岸布置开敞式侧槽溢洪道。大坝坝型为碾压式沥青混凝土心墙堆石坝，坝顶高程802.50m，坝轴线全长178m，坝顶宽6m，最大坝高52m。大坝上、下游采用砂岩堆石料及混合石渣料分区填筑，上游坡比1∶1.5、1∶3，下游坡比1∶2.25、1∶2.25、1∶2，坡脚设堆石贴坡排水。

2 坝料分区方案拟定

青龙水库大坝初始剖面如图1所示(记为方案1)。该分区方案的大坝上游下部和下游干燥区均采用石渣料填筑，考虑到蓄水后在水压力作用下心墙存在向下游弯曲的趋势，为抵抗弯曲变形，于坝体下游临心墙一侧设置了顶宽3m、坡比1∶0.8倾向下游的堆石料区，以增强结构安全性。

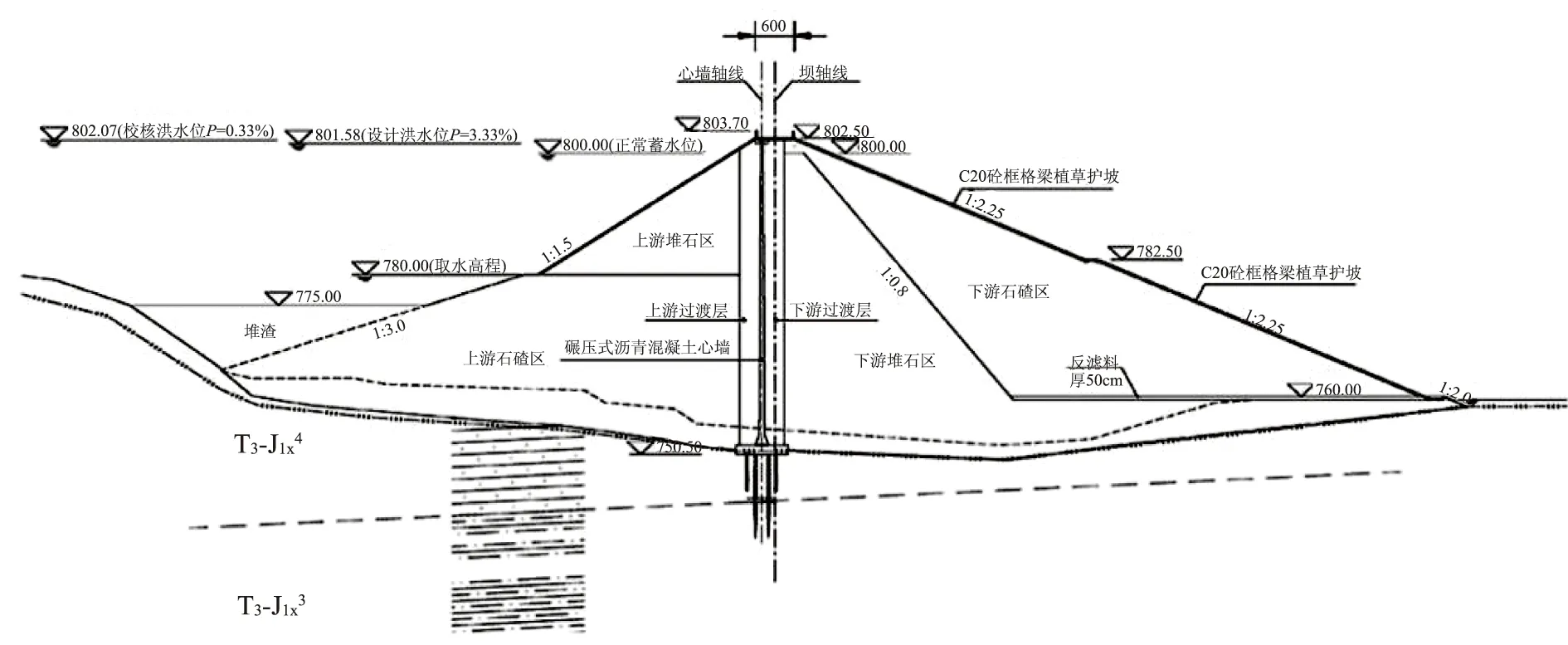
图1 方案1大坝典型横剖面图(单位：m)

经分析该坝体分区方案：上游侧坝壳料的下部为石渣料，在水库完建期或石渣料变形过大时，心墙存在向上游弯曲的趋势，为了抵抗这一趋势，可考虑在上游坝壳下部的心墙侧设置一个梯形的堆石分区提供一定抗力；同时下游堆石区相较类似工程尺寸略为保守，由于堆石料单价高，值得研究优化下游堆石区尺寸的可能性。根据该思路，可通过研究缩小下游堆石区尺寸以节省堆石料，并将节省的堆石料用于在上游下部的新增堆石分区，从而在不增加堆石用量及工程总体投资的基础上获得更合理的分区布置，以提高心墙的设计安全储备。

据此拟定优化方案2—7。其中方案2—4在方案1的基础上，将下游堆石区的坡比由1∶0.8分别调整为1∶0.5、1∶0.2、1∶0(垂直)，可用于分析下游堆石区范围对坝体应力变形场的影响，如图2所示。

图2 方案2—4大坝典型横剖面图(单位：m)

方案5—7在对方案1—4进行优选的基础上，基于方案2在上游坝壳下部增设顶坡比1∶0.5的堆石区，顶宽分别为3、5、7m，用于分析上游坝壳下部设堆石区及其范围对坝体应力变形场的影响，如图3所示。

图3 方案5—7大坝典型横剖面图(单位：m)

3 计算模型及材料参数

3.1 数值模型及计算工况

对各方案进行二维有限元计算，计算取典型断面的大坝+基岩的二维整体模型，在模型地基底部施加法向和横向的固定约束，在地基两侧的铅直面上施加法向的固定约束，坝坡及临空面自由。以方案1为例，共剖分了6903个节点和6887个单元，其中心墙剖分了291个节点和174个单元，典型计算网格如图4所示。

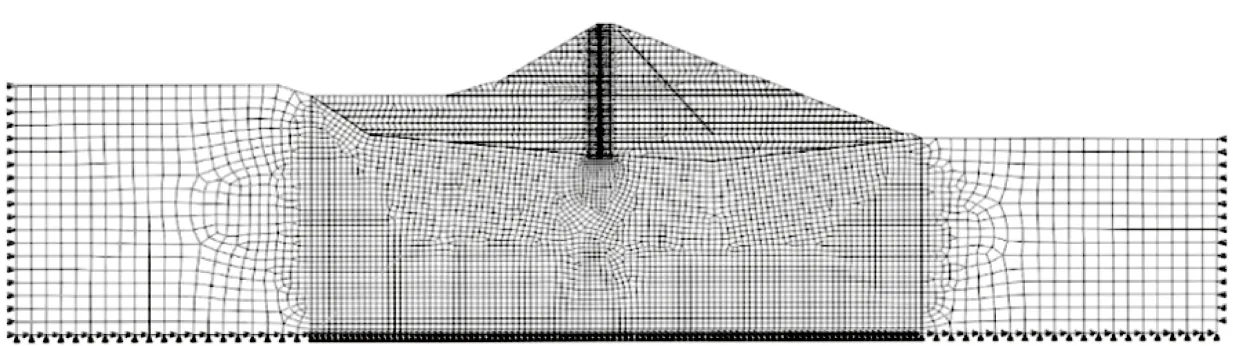
图4 典型的计算网格剖分图

考虑到本工程的正常蓄水位与设计及核洪水位相差不大，在布置方案初选阶段，拟定2种分析工况：完建工况和正常蓄水位工况。

考虑到坝体实际施工是分层碾压填筑，且主要筑坝材料(堆石体、沥青混凝土心墙等)均表现出非线性特性，故在进行有限元模拟时也采用逐级加载的方式。首先计算坝体填筑施工前的初始应力场，然后模拟逐级填筑，荷载逐级加载。每次加载填筑抬升2～3m，心墙和坝体同步填筑上升。

3.2 材料本构及计算参数

堆石、石渣和沥青混凝土心墙等材料具有非线性的应力应变特性，采用邓肯—张E-B模型模拟，计算参数见表1。地基岩体及混凝土采用弹性模型模拟，计算参数见表2。考虑的坝高不大，变形水平不高，计算时未在两侧过渡料与沥青混凝土心墙间设置接触面，这样使得沥青混凝土心墙具有一定的“悬挂”效应，应力计算结果偏于安全。

表1 坝体土石料计算参数

表2 岩体及混凝土计算参数表

4 计算结果

4.1 计算结果分析

对7种堆石、石渣分区的组合方案进行二维有限元静力分析，各方案主要变形计算结果见表3，应力计算结果见表4。

表3 各方案主要变形计算结果

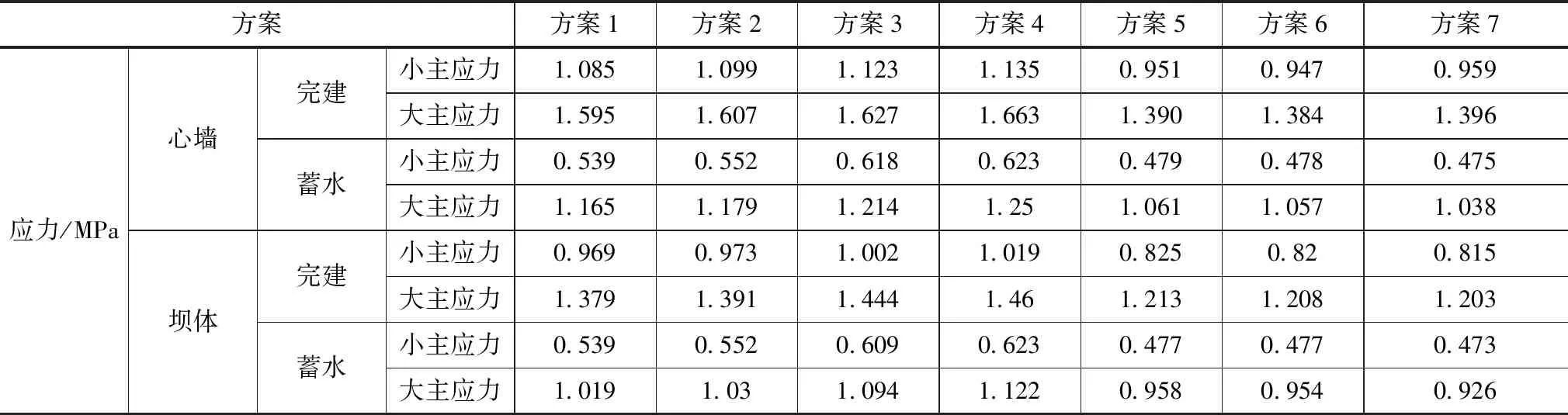
表4 各方案主要应力计算结果

通过对各方案在完建及正常蓄水工况下应力及变形特征值的分析，各方案的坝体和心墙的位移场、应力场分布均符合一般规律，且位移场和应力场的最大值均在允许范围内，这说明坝体和心墙结构受力合理，发生压裂、拉裂+破坏的可能性比较小。通过对各方案应力及变形特征值的对比，方案1—4随着下游堆石区尺寸的减小，坝体和心墙的应力及变形特征值逐渐增大。方案5—7在上游下部增设了堆石区，坝体和心墙的位移及应力状态较前述方案均有明显改善，随着上游下部堆石区尺寸的增大，坝体和心墙的位移及应力状态也表现出进一步改善的趋势，但改善幅度不明显。

结合各方案的堆石、石渣用量综合分析，方案6的堆石、石渣用量和原方案1大致可平衡，不新增堆石用量；同时方案6较方案5的应力变形状态有一定改善，较原始方案改善明显。虽然方案7的应力变形状态得到进一步改善，但其改善幅度在减小，同时较方案1增加了堆石用量，工程投资增加，技术经济指标不如方案6。初步认为方案6的优化效果较为优异。

4.2 目标函数判别

为了量化评价优化效果，研究工作在常见的单纯以投资作为控制指标的目标函数基础上引入了应力、变形修正系数，并定义了青龙水库沥青混凝土心墙堆石坝分区优化的目标函数：

F(Ai，Si，Di)=(47.59Ai1+20.31Ai2)SiDi

(1)

(2)

(3)

式中，F—方案的优化目标；47.59和20.31—堆石料、石渣料的材料单价；Ai1—方案i堆石料用量，万m3；Ai2—方案i石渣料用量，万m3；Si—方案i的应力修正系数；Si1—方案i各工况下坝体应力的最大值；Si2—方案i各工况下心墙应力的最大值；Di—方案i的变形修正系数；Di1x—方案i各工况下坝体x方向位移的最大值；Di1y—方案i各工况下坝体y方向位移的最大值；Di2x—方案i各工况下心墙x方向位移的最大值；Di2y—方案i各工况下心墙y方向位移的最大值。

该目标函数考虑了优化的经济效益及应力变形改善情况，其值越小，则优化效果越显著。经计算得到各方案优化成果的目标函数值见表5。

表5 分区优化成果

从目标函数计算结果分析，方案6的目标函数值最低，表明方案6的优化效果最显著。这与分析结论一致，说明结果是合理的。因此推荐方案6为坝体分区优化的推荐方案。

5 推荐方案地震作用效应分析

为了验证推荐坝料分区方案在地震工况下的安全性，基于二维有限元分析手段采用拟静力法对推荐坝料分区方案进行地震作用效应分析验证。

拟静力法假定坝体所有节点在地震作用下其地震惯性力均为水平方向的惯性力，根据具体计算条件综合考虑选取计算工况为：①完建工况下+指向下游的地震惯性力；②完建工况+指向上游的地震惯性力；③正常蓄水位工况+指向下游的地震惯性力。

经计算，地震作用下推荐坝料分区方案坝体及心墙的动位移响应值见表6，应力响应值见表7。

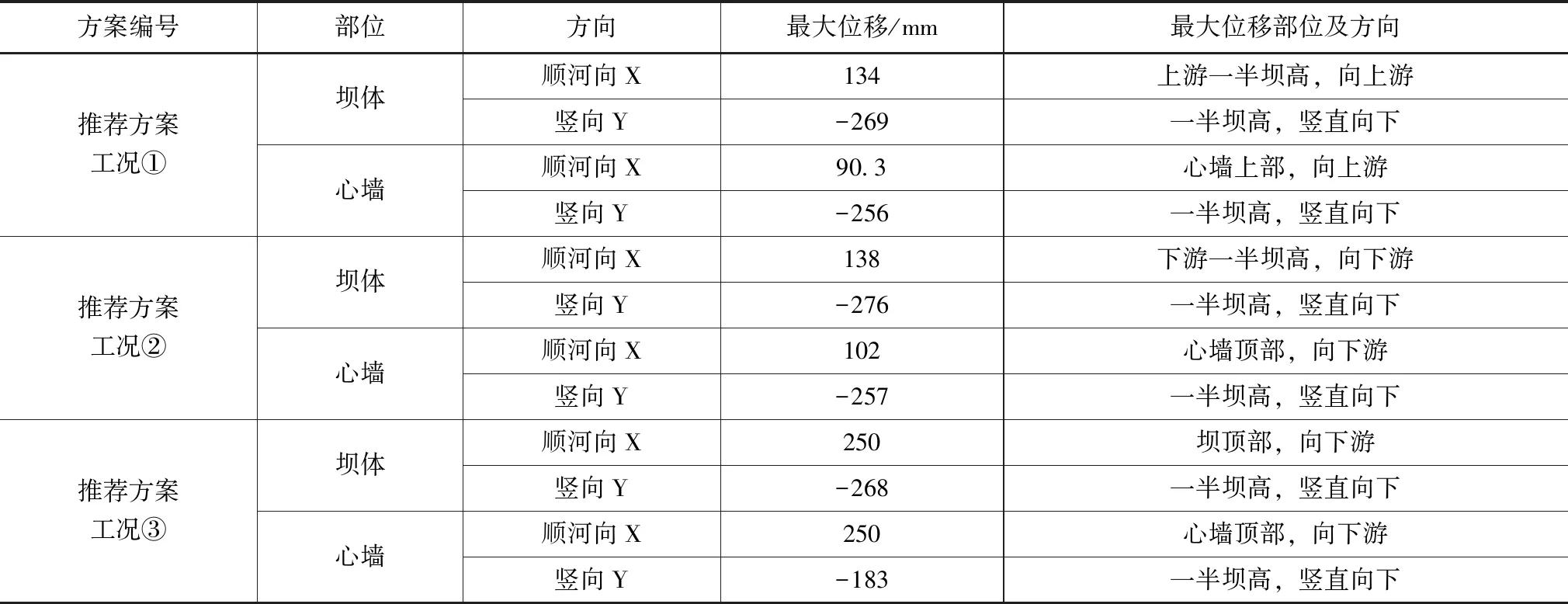
表6 推荐坝料分区方案地震作用下土石坝坝体及心墙动位移响应值

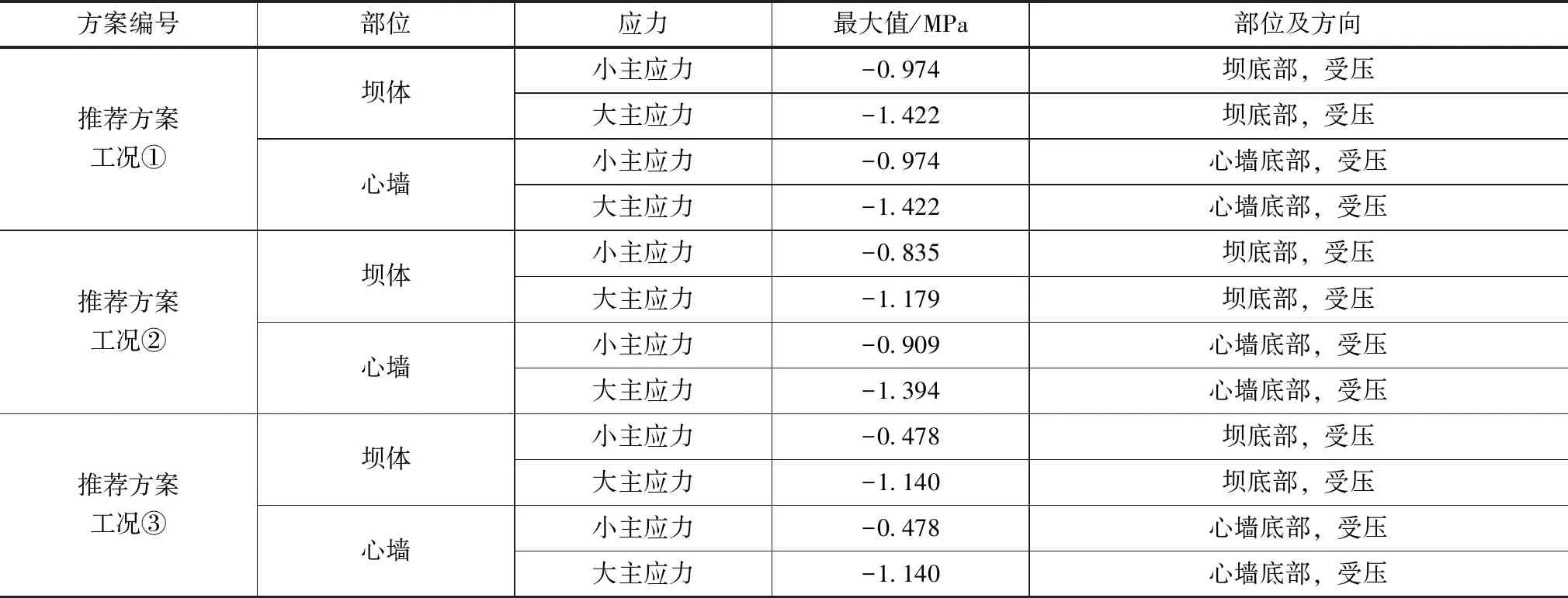
表7 推荐坝料分区方案地震作用下土石坝坝体及心墙动位移响应值

经分析可知：相比未发生地震的工况，在地震作用下坝体及心墙的顺河向位移均有所增加，最大幅度达48.8%；各工况竖向位移与地震前差异不大，最大达5.51%；坝体及心墙的大、小主应力均出现了增加，最大达19.5%。

推荐坝料分区方案在地震工况下的坝体和心墙位移场、应力场分布均符合一般规律，位移场和应力场的最大值均在允许范围内，这说明坝体和心墙结构受力合理，发生压裂、拉裂破坏的可能性比较小。推荐坝体分区优化方案在地震作用下的应力和变形均在合理范围内，推荐坝料分区优化方案是可行的。

6 结语

本论文基于坝料分区的初始布置方案，基于不

(1)各方案坝体和心墙的应力位移场符合一般分布规律，坝体和心墙受力合理，发生压裂、拉裂破坏的可能性比较小；各方案应力及变形特征值的对比分析表明，随着下游堆石区尺寸的减小，坝体和心墙的应力及变形特征值逐渐增大。

(2)在上游下部增设堆石区可使坝体和心墙的位移及应力状态得到明显改善，且随着上游下部堆石区范围的逐渐增大，改善效果逐渐增强。

(3)各方案的判别结果分析表明，方案6的优化效果最显著，应力变形状态的改善效果明显，同时该方案的堆石、石渣用量和原方案大致可平衡，投资指标得到控制；选取方案6为坝体分区优化的推荐方案。

(4)在地震作用下坝体及心墙的顺河向位移均有所增加，最大幅度达48.8%；各工况竖向位移与地震前差异不大，最大达5.51%；坝体及心墙的大、小主应力均出现了增加，最大达19.5%；各应力和变形均在合理范围内，推荐方案在地震作用下的是安全的坝料分区方案。