引水隧道最佳支护系统工程数值建模分析

刘方亮

(新疆额尔齐斯河流域开发工程建设管理局，新疆 乌鲁木齐 830000)

由于岩体的不连续性、各向异性、非均质性和非弹性性质，使用经验和数值方法对岩体建模是一项非常困难的工作[1-2]。在开挖工程的初始阶段，关于岩体的强度特性、变形模量、原位应力和水文特性的详细数据不可用[3]。为了处理详细项目数据的不可用性，像岩体分类方法这样的经验方法是用于解决工程问题重要方法[4]。在任何地下结构的设计、支护系统推荐和数值模拟输入参数的确定中，经验方法使用定义的输入参数[5]。经验方法将岩体定量地划分为具有相似特征的不同类别，以便于理解和建造地下工程结构。尽管其应用广泛，经验方法并不评估支护系统的性能、应力再分布和隧道周围的变形[6]。因此，在设计最佳地下结构和支护系统时，考虑这些参数是非常重要的。用数值方法可以解决经验方法的这一不足。

数值模拟在土木和岩石工程领域越来越受到重视，常常用于预测岩体对各种开挖活动的响应[7]。数值方法在分析分布应力对岩体行为的影响和岩体环境中结构的设计等方面具有简便、成本较低和耗时较少的优点[8]。同时，数值模拟为解决与隧道形状、尺寸、矿井布局和顶板支护系统设计相关的复杂工程问题提供了良好的思路，从而在采矿结构的整个计划作业寿命期间实现一致的技术经济可行性能[9]。由于岩石力学领域技术的进步，不同的研究人员开发了不同的数值方法，如有限差分法(FDM法)、有限元法(有限元法)和边界元法(边界元法)，用于解决工程相关问题。在这些连续体数值方法中，有限元法主要用于解决岩石工程问题[10]。

在本研究中，对岩体使用岩体分级方法(RMR)和隧道质量指数(Q值)进行评估。基于应力、总变形和隧道周围的塑性屈服厚度，采用基于有限元法的Phase2软件，分析了2种不同支护系统相互作用下的岩体特性，为隧道选择合适的支护系统，这对该领域的工程实践具有重要意义。

1 岩体分级方法

该工程的隧道是直径为3.7m的马蹄形隧道。不同的研究人员根据土木和采矿工程案例研究开发了各种岩体分类方法用于岩体的评估和分类。由于在输入参数方面的灵活性和广泛性，RMR和Q值是常被使用的2种分类方法，本研究中也使用这2种分类方法。

RMR分类方法[5]使用单轴抗压强度(UCS)、岩石质量名称(RQD)、不连续面间距、不连续面条件、地下水条件和不连续面方向作为岩体表征和分类的输入参数。通过将这6个参数的等级相加来计算RMR。

Q值分类系统根据岩石质量指标(RQD)、节理组数(Jn)、节理粗糙系数(Jr)、节理蚀变程度系数(Ja)、节理减水系数(Jw)和地应力折减系数(SRF)将岩体环境分为不同的类别。该系统的Q值表明了岩体的质量，Q值由公式(1)进行计算，基于从RMR和Q值获得的结果，沿隧道轴线的岩体被划分为3个岩土单元。表1给出了RMR和Q值分类方法的结果。

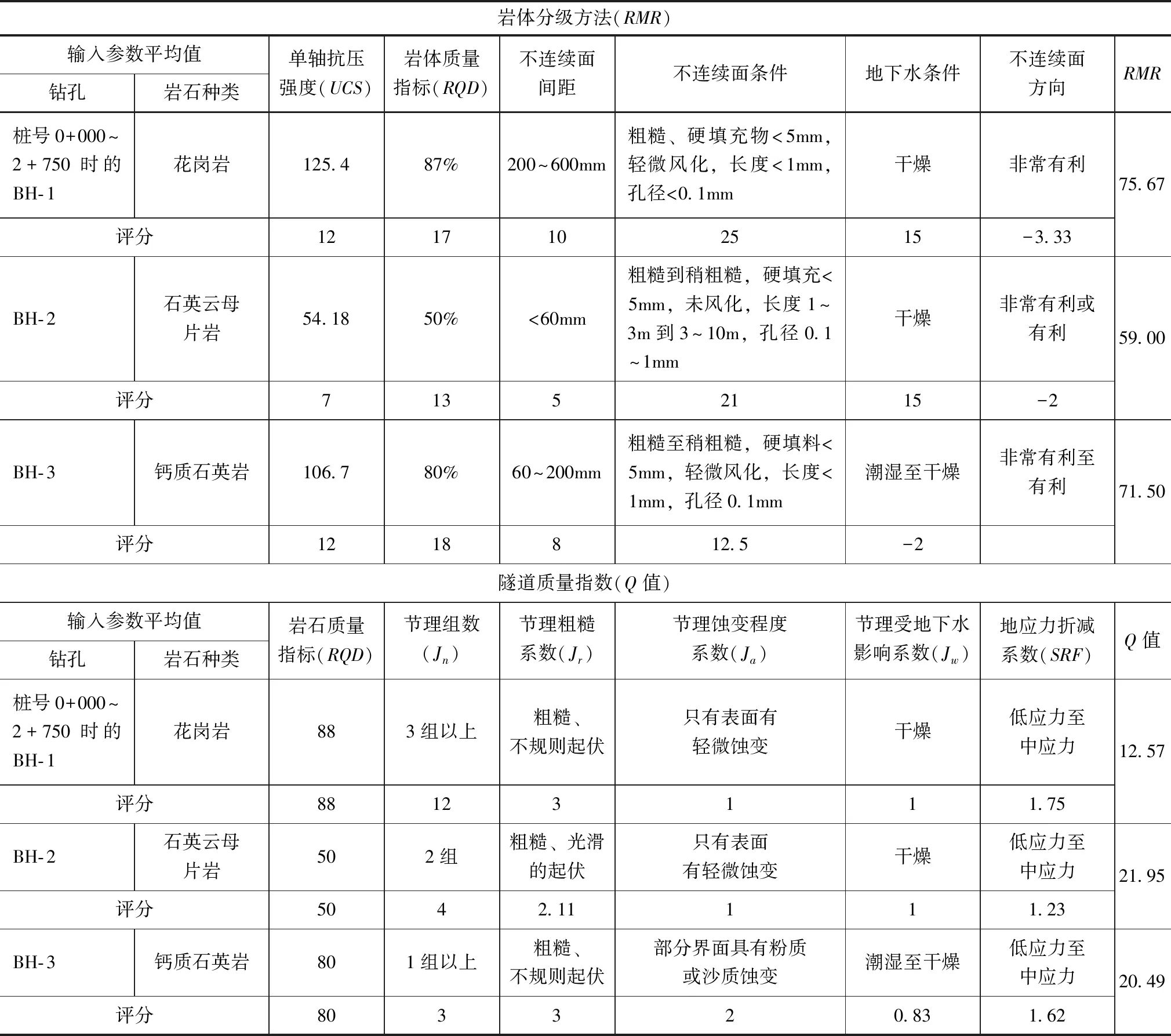
表1 岩体分级结果

(1)

2 原位应力

在本研究中，垂直应力计算公式为：

σv=γH

(2)

式中，γ—岩体的单位重量,g/cm3；H—覆盖层的高度,m。

水平应力计算公式为：

(3)

对于每个岩土单元，使用公式(2)和数值建模(3)确定垂直和水平应力，计算结果和所采用的支护系统见表2—3。

表2 应力计算

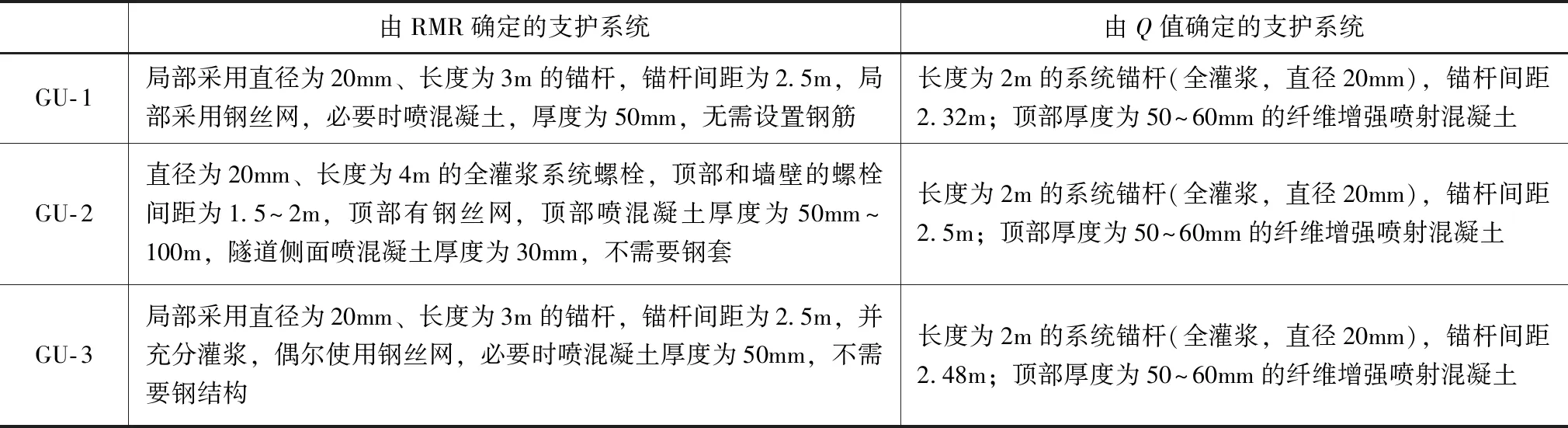
表3 2种方法确定的支护系统

3 结果和讨论

基于有限元的软件Phase2用于分析隧道的设计分类方法。数值分析采用3阶段来确定地应力。在模拟模型的第一阶段，研究了地应力分布。在下一阶段，分析诱导应力分布、屈服点和位移。在最后阶段，确定了推荐分类方法。

3.1 GU- 1的数值分析

对于这一部分，开挖前的初始应力σ1为19.36MPa，开挖后隧道拱顶和侧壁的σ1分别为0和26MPa。开挖前最大原始应力σ3为5.35MPa，开挖后隧道拱顶和侧壁的σ3均为0.70MPa。对于这一部分，最大应力集中出现在隧道侧壁。如图1(a)所示，开挖后和支护前，隧道顶部和底部的最大变形为1.84mm。拱顶和侧壁的塑性区(屈服区为50%)厚度很小，可以忽略不计；然而，在底部，它大约为1112mm，如图1(b)所示。

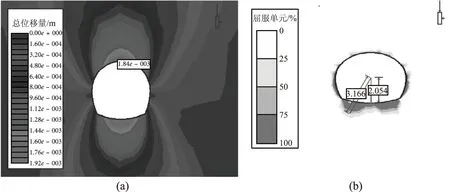
图1 前塑性区的最大位移和厚度

对于RMR支护，锚杆的最大轴向应力为92.05MPa，喷混凝土构件的最大轴向力为0.972MN。对于支护，锚杆的最大轴向应力为102.05MPa，喷混凝土构件的最大轴向力为4.35MN。模拟模型中安装RMR和Q推荐支架后的隧道总位移与支护前相同，即RMR支架为2.30mm，Q支架为2.30～2.10mm，如图2所示。

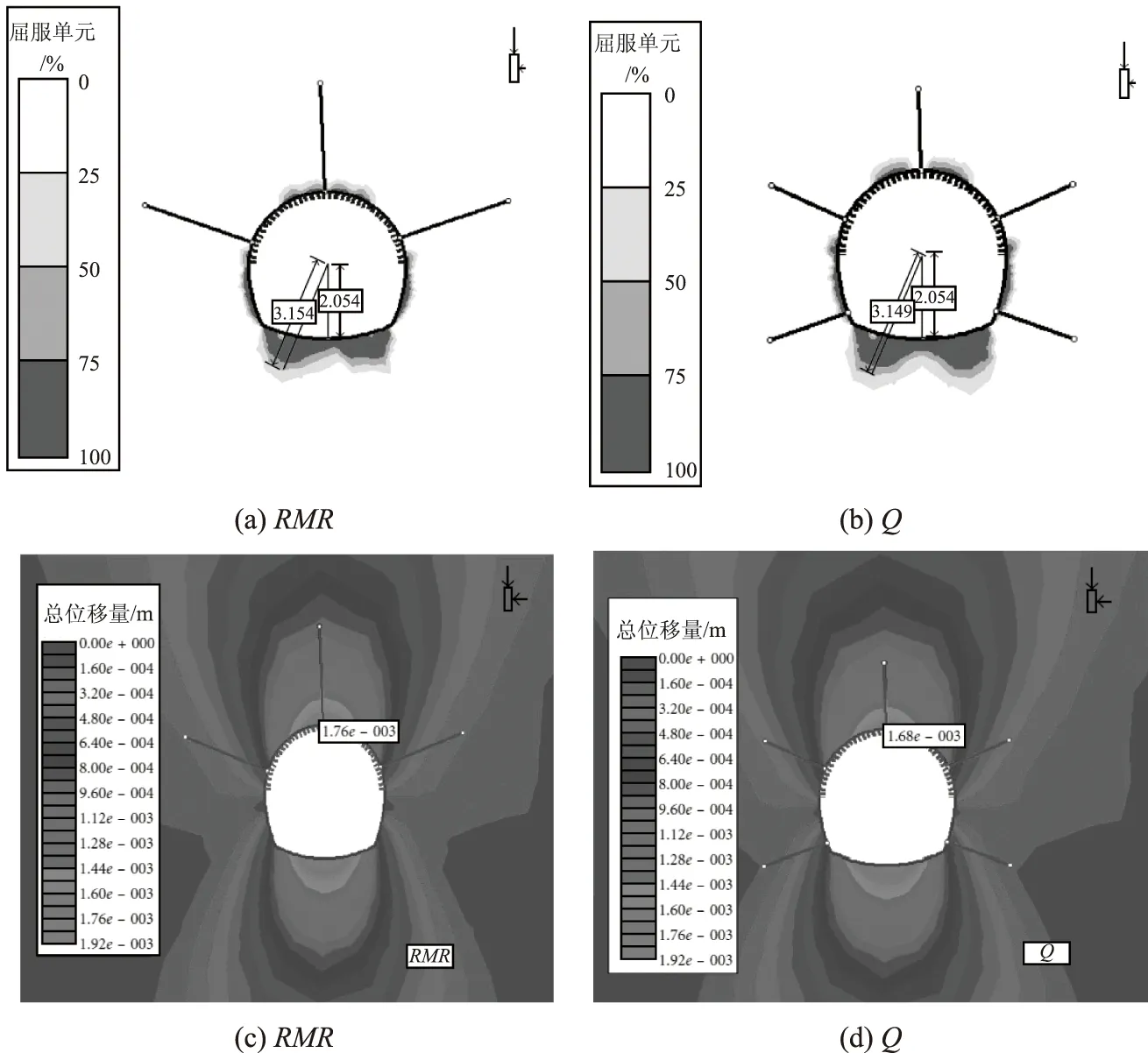
图2 2种支护系统的屈服区和变形

经过对RMR和Q型支架模拟模型的对比分析，Q型支架的锚杆最大轴向应力和喷射混凝土最大受力均大于RMR型支架，Q型支架的围压大于RMR型支架，Q型支架的总位移与RMR型支架相比从1.84mm减小到1.68mm，Q型支架的屈服区厚度减小略大于RMR型支架。因此，Q支护比RMR支护对于GU-1段更有效。

3.2 GU- 2的数值分析

对于GU-2段，开挖前的初始应力σ1为11.84MPa，开挖后隧道拱顶和侧壁的σ1分别为0.85 和4.25MPa。开挖前的初始应力σ3为2.10MPa，开挖后隧道拱顶和侧壁的σ3均为0MPa。最大应力集中出现在隧道侧壁，如图3所示。

图3(a)中，开挖后和支护前，隧道顶部和底部的最大变形为3.15mm。图3(b)显示了支架顶部、侧壁和底部的塑性区厚度(50%)分别约为4638、1117和5468mm。

图3 前塑性区的最大位移和厚度

与RMR支架相比，在模拟模型中安装Q支架后，发现隧道周围的σ1、σ3、屈服区和塑性区得到了改善。对于RMR支护，锚杆的最大轴向应力为193.24MPa，喷射混凝土构件的最大轴向力为5.35MN。对于Q型支护，锚杆的最大轴向应力为119.82MPa，喷射混凝土构件的最大轴向力为3.06MN。如图4所示。

图4 2种支护系统的屈服区和变形

在模拟模型中安装RMR和Q建议支架后，隧道内的总位移在RMR支架的情况下从3.15mm降至2.40mm，在Q支架的情况下从3.15mm降至2.55mm。通过对Q型支架模拟模型的对比分析，锚杆的轴向应力小于RMR支架，Q型支架的围压大于RMR支架，Q型支架的塑性区比RMR支架有更大的改善，RMR和Q型支架的总位移减小幅度大致相同。因此，Q支护似乎比RMR支护GU-2部分更有效。

3.3 GU- 3的数值分析

对于GU-3段，开挖前的初始应力σ1为11.52MPa，开挖后隧道拱顶和侧壁的σ1分别为0 和21MPa。开挖前的初始应力σ3、开挖后隧道拱顶和侧壁的初始应力σ3均为0.20MPa。对于这一部分，最大应力集中出现在隧道侧壁。开挖后和支护前，隧道顶部和底部的最大变形为0.990mm，如图5(a)所示。顶部塑性区(50%)厚度约333mm，侧壁小到可以忽略不计；但是，底部的直径约为1001mm。支承前的屈服区和屈服单元如图5(b)所示。

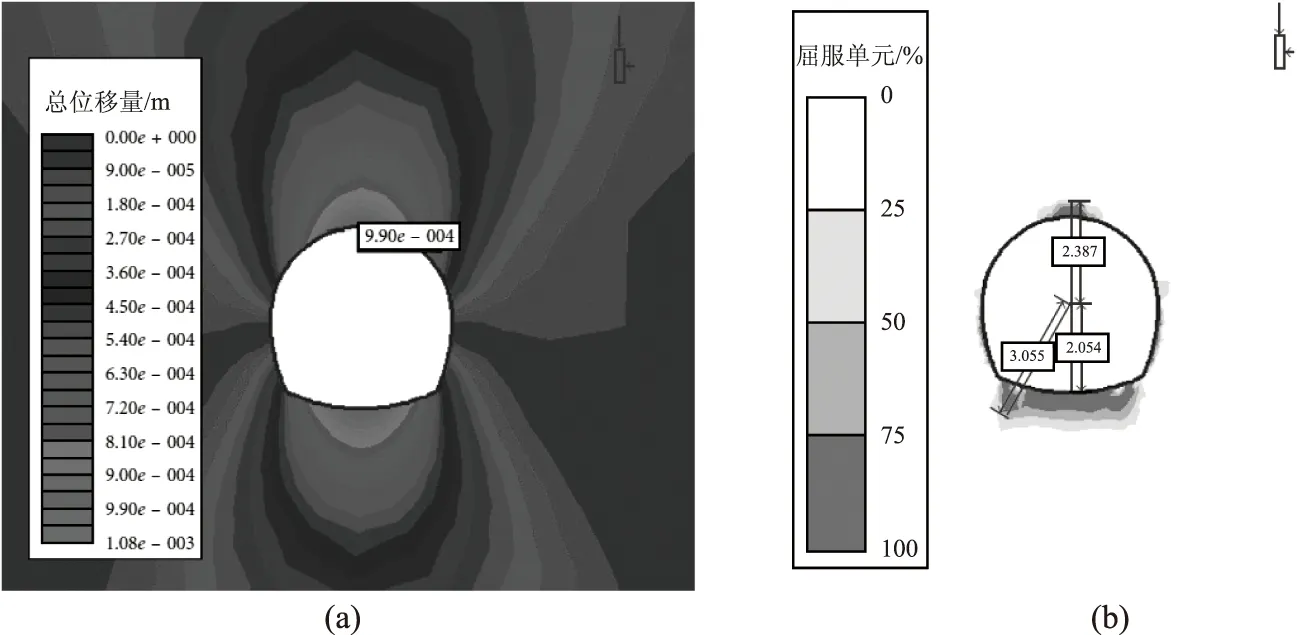
图5 前塑性区的最大位移和厚度

对于RMR支护，锚杆的最大轴向应力为34.50MPa，喷射混凝土构件的最大轴向力为8.52MN。对于Q型支架，锚杆的最大轴向应力为46.70MPa，最大轴向力为1.13MN。安装RMR支架后，与Q支架相比，塑性变形厚度减小。在模拟模型中安装RMR和Q推荐支架后，隧道中的总位移在RMR支架的情况下从0.990mm减少到0.810mm，而在Q支架的情况下没有减少，如图6所示。

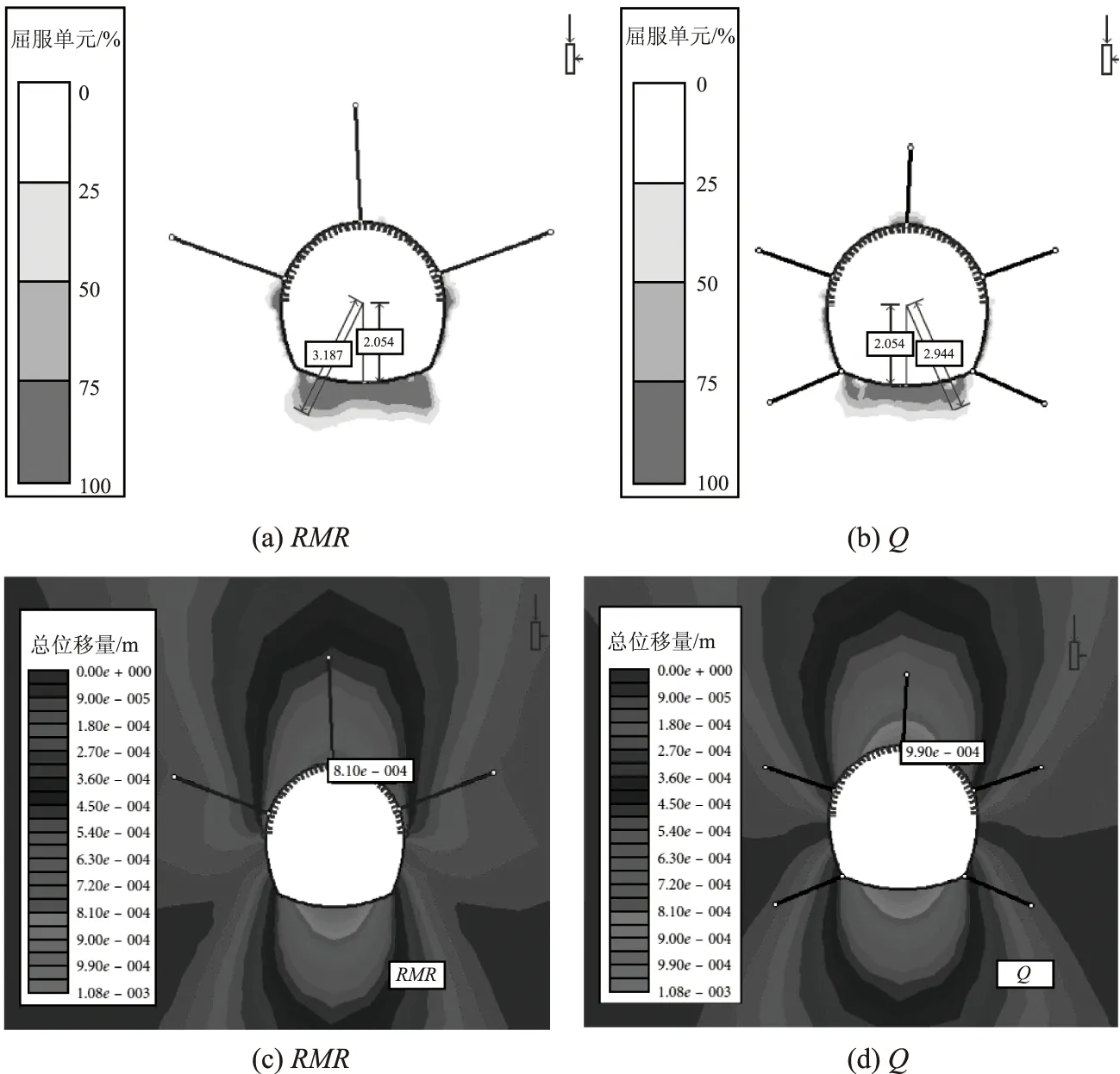
图6 2种支护系统的屈服区和变形

4 结论

本研究采用经验和数值方法评价岩体质量，估算引水隧洞所需的支护单元，并在支护系统安装前后对隧洞进行稳定性分析，以选择最佳支护系统。

(1)对于Q支架，塑性区厚度最大值在底部的GU-1从1112mm减少到1095mm，在顶部的GU-2从4638mm减少到3716mm，在底部的GU-3从1001mm减少到894mm。

(2)对于RMR分类方法，塑性区厚度在底部从1112mm减少到1100mm，而对于GU-2和GU-3，它没有减少。

(3)Q分类方法对GU-1和GU-2是较好的支护方法，而RMR分类方法对GU-3则是更好的选择。

(4)由于目前研究的局限性，数值模拟精确计算还有待深入探讨，这也是后续工作的重点之一。