基于非结构网格的三种CSEM有限元三维正演系统分析

周 峰 张志勇 陈 煌 汤井田 邓居智 李 勇

(①东华理工大学放射性地质与勘探技术国防重点学科实验室，江西南昌 330013；②东华理工大学地球物理与测控技术学院，江西南昌 330013；③中南大学地球科学与信息物理学院，湖南长沙 410083；④中国地质科学院地球物理地球化学勘查研究所自然资源部地球物理电磁法探测技术重点实验室，河北廊坊 065000)

0 引言

可控源电磁法(Controlled Source Electromagnetic Method，CSEM)具有抗干扰能力强、工作效率高、测量精度高等诸多优点，是研究中浅部电性结构的主要地球物理方法之一，广泛应用于固体矿产、水文、石油天然气普查、地热田勘探、环境地质调查及环境与工程地球物理勘查等领域[1-3]。目前，实际勘探任务大多以复杂三维地质构造为主，传统的一维、二维假设条件下的资料解释技术不能满足目前的地质解释要求，迫切需要开发三维可控源电磁资料解释技术。正演是反演的基础，因此国内外学者都致力于任意复杂地形的地电结构CSEM三维正演模拟研究，寻求快速、高精度的三维正演方法。

针对CSEM三维正演问题，学者们做了大量研究工作。首先针对场源奇异性导致正演精度损失的问题，将CSEM正演分解为总场算法和二次场算法。二次场算法能够去除场源奇异性，但无法实现任意复杂地形条件下地电模型的正演模拟[4-9]。基于总场算法的求解方案早期主要是以伪delta函数刻画场源问题，一定程度上降低了场源奇异性，但无法从根本上解决场源的奇异性问题[10-12]，甚至会加剧场源加载的难度。为此，得益于近年来非结构化网格离散技术的发展，广泛应用局部加密技术降低场源奇异性，结合delta函数场源积分能够避免场源加载的困难[13-17]。随后，基于自适应的有限元正演技术被广泛应用于CSEM三维正演模拟，进一步弥补了场源奇异性带来的精度损失[14,18]。在实现大规模的电磁快速正演求解方面，早期基于节点有限元结合散度矫正的技术被应用，虽然弥补了电场方程迭代求解不收敛现象，但同时降低了正演求解的精度[7]。之后，基于电场双旋度方程的矢量有限元直接求解技术被提出，虽大幅度提高了正演方程的求解精度[13,16,19]，但无法避免双旋度结构带来的空解问题，使常规Krylov子空间迭代求解困难，导致直接求解的三维反演算法对内存的需求更高，限制了该算法的应用。为了使电场双旋度方程可用于迭代计算，Schwarzbach等[14]开展了E-Φ方程的CSEM正演模拟(E和Φ分别表示电场和电标量位)，取得了一定效果，但亦无法从根本上解决迭代收敛慢等问题。之后，有学者提出基于势位(如A-Φ势[13,20-25]，A表示磁矢量位)的三维电磁正演求解系统，在一定程度上扩展了三维电磁求解系统的种类，计算精度和效率得到一定的改善。

1 基本理论

1.1 CSEM偏微分方程

在准静态条件下，可控源电磁法满足Maxwell方程组，取时间因子e-iωt，其频率域表达式为

(1)

(2)

(3)

(4)

为消除磁场参数，将式(1)代入式(2)，可得

(5)

上式即是三维CSEM需满足的电场方程。

有限元技术的基函数经历了节点基函数到矢量基函数的发展。为了消除伪解并遵循电场法向不连续性特征，基于矢量基函数的有限元技术求解电场方程成为目前主流方法。但是，可控源电磁法中的梯度电场是由地表和地下电导率不连续界面上的积累电荷产生的，导致基于电场方程的矢量有限元法很难实现梯度电场的模拟，而该梯度电场对于可控源电磁法非常重要，这一矛盾被称为矢量有限元的空解难题。因此，有学者将目光聚焦到A-Φ耦合势方程，进行了较系统的研究。

电场E和磁感应强度B可用矢量位A和标量位Φ分别表示为

(6)

(7)

将式(6)和式(7)代入式(5)可得A-Φ耦合势方程

(8)

根据电荷守恒以及欧姆定律，可得辅助方程

(9)

联立式(8)和式(9)，可得基于双旋度结构的A-Φ耦合势可控源电磁方程

(10)

(11)

最后形成系统方程

(12)

式(12)的求解系统采用节点基函数对矢量位A和标量位Φ进行离散，可获得拉普拉斯结构的A-Φ可控源电磁法求解方程。另外，本文通过扩边加载截断边界条件，实现电磁场在无穷远处消失为零。

1.2 有限元分析

以式(5)为控制方程，应用Galerkin法推导有限元方程。设余量为

(13)

令re在计算区域T满足

∭TN·redT=0

(14)

式中N为矢量基函数。将式(13)代入式(14)，可得

(15)

对式(15)应用第一矢量格林定理，可将其简化为

(16)

式中：Γ=∂T表示求解区域外边界；n为外边界单位法向量。另外，扩边处理使得求解区域足够大，因此式(16)中的面积分项可忽略不计。

同理，对式(10)应用Galerkin法进行推导并化简，最终的有限元积分方程为

(17)

(18)

式中L表示有限元中的节点基函数。

同理，对式(12)应用Galerkin法进行公式推导及化简，得到最终的有限元积分表达式为

(19)

(20)

(21)

下面分别叙述如何选择上述三类方程有限元基函数。

(1)对电场方程采用矢量有限元进行离散。对于每一个四面体单元e，任意点(x,y,z)处的电场可由各条棱边的电场Ei和矢量基函数Ni表示为

(22)

式中矢量基函数Ni可用节点基函数[29]表示为

(23)

式中：li为棱边i的长度；Lj1与Lj2表示该棱边两个节点的基函数，具体标号如图1所示。

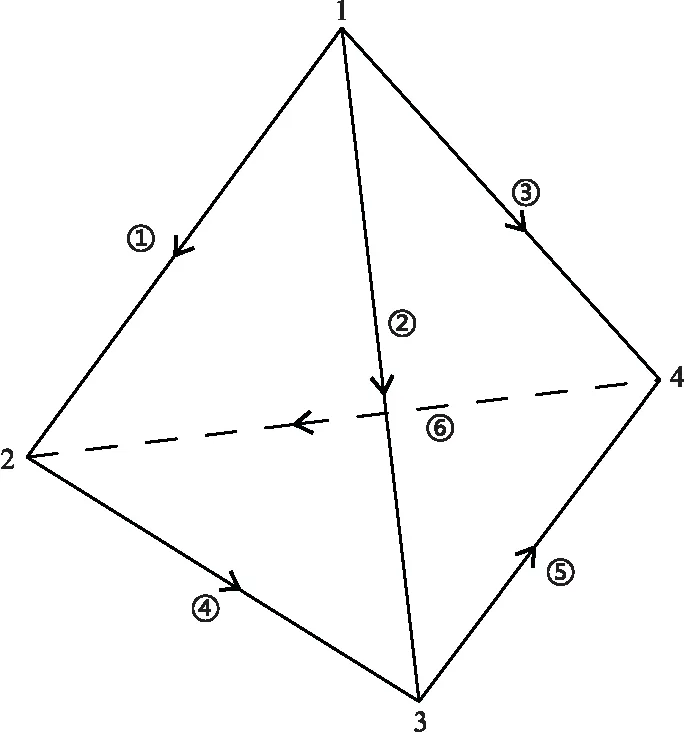
图1 四面体单元棱边和节点关系1～4表示节点编号，①～⑥表示棱边编号

(2)对于双旋度结构的A-Φ耦合势CSEM方程，矢量位A和标量位Φ可分别采用矢量基函数和节点基函数进行描述

(24)

(3)拉普拉斯结构的A-Φ耦合势CSEM方程，矢量位A和标量位Φ可采用节点基函数表示为

(25)

因此，通过以上不同的离散形式可得到三种不同的CSEM求解系统，即电场方程、双旋度结构的A-Φ耦合势和拉普拉斯结构的A-Φ耦合势，本文结合稳健的直接求解器PARDISO和Krylov子空间算法对这三种求解系统进行对比分析[27,30]。

1.3 场源加载

对于CSEM三维正演来说，源项加载不准确和场源的奇异性会严重影响正演的求解精度。针对这两种问题，常用的场源处理技术主要包含两类：①二次场算法，其目的是解决源的奇异性问题，但需要计算具有解析表达式的一次场，因而对复杂地电模型模拟的局限性较大；②基于总场算法并结合偶极源积分实现场源加载，具有较好的适用性，但仍无法避免场源奇异性问题。为此，本文采用偶极源积分结合非结构化网格局部细化技术，不仅能有效降低场源奇异性，还能实现场源的统一表示形式。

对于电场方程的三维CSEM有限元系统，场源加载可表示为

(26)

对于x方向电性源来说，源线段置于四面体棱边上，因此有

∭T(Nxix+Nyiy+Nziz)·[Θ(xi+1)-Θ(xi)]δ(y-y0)δ(z-z0)ixdT

(27)

式中：Θ表示Heaviside函数；δ是delta函数；Nx、Ny、Nz分别表示矢量基函数N的三个分量；ix、iy、iz表示笛卡尔坐标系下沿坐标轴方向的单位向量；(x0,y0,z0)表示偶极源的中心坐标。

垂直磁偶源M的表达式为

M=mδ(x-x0)δ(y-y0)δ(z-z0)iz

(28)

(29)

(30)

由上式可得

(31)

将场源置于四面体单元内，上式中的面积分项(公式右边第二项)等于零，因此积分式只剩下右边第一项。若采用电性源的形式加载磁性源，场源的积分公式与电性源一样，在此不再叙述。

2 算例分析

为了分析上述三种求解系统对三维CSEM的模拟效果，设计了两个模型进行正演计算。一个模型是存在解析解的均匀半空间，另外一个是无解析解的低阻地电模型。测试本文开发算法的计算机配置为：内存32G，intel(R)CoreTMi7-9700 CPU@ 3.00GHz。

2.1 模型1：均匀半空间

2.1.1 算法验证

对均匀半空间模型加载一个正方形的垂直磁偶源，磁偶源是大小为1.0m×1.0m的线框，位于求解区域的中心。地下背景电阻率为100Ω·m，空气电阻率为108Ω·m。求解区域大小为[-30km,30km]3。为了降低场源的奇异性，对场源进行局部加密，被离散为27个小的线段，如图2所示。

图2 垂直磁偶源网格剖分示意图

计算3Hz的垂直磁偶源电磁响应。整个求解区域被剖分成403789个四面体单元，471329条边和66521个节点。沿x方向等间距设置观测点，点距为120m，共50个观测点。

采用Krylov子空间的GMRES算法结合ILU(0)预条件因子分别对前述两种结构的A-Φ耦合势有限元方程进行求解，采用PARDISO直接求解器对电场方程进行求解，得到磁场垂直分量Hz的实部和虚部，并与解析解进行对比(图3)。两种结构的A-Φ耦合势方程组求解的收敛曲线见图4。

从图3可知，三种求解系统的结果与解析解都高度吻合，误差基本都小于1.5%。从图4的收敛曲线可知，双旋度结构的A-Φ耦合势方程组求解需要迭代3000次，相对残差为2.31×10-15，而拉普拉斯结构的A-Φ耦合势方程组求解仅需200次，相对残差为1.9×10-15。

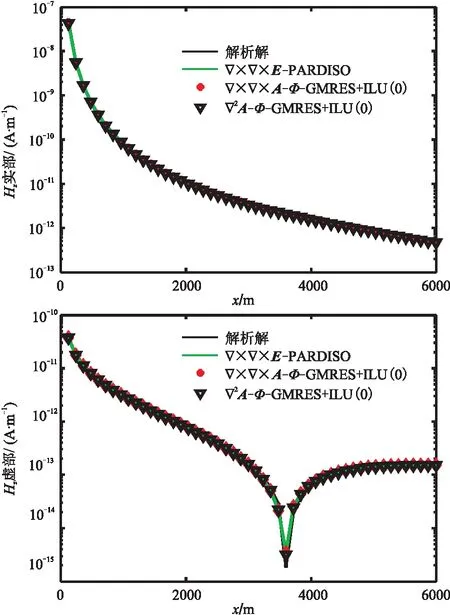
图3 3Hz磁场Hz实部(上)和虚部(下)响应曲线

图4 3Hz磁场Hz的收敛曲线

本文还计算了100Hz时垂直磁偶源的电磁响应。求解区域被离散为814255个四面体单元、675519条边单元和138736个节点，并沿x方向等间距设置观测点，间距为20m，共50个观测点。图5展示了100Hz时的电磁响应。两种结构的A-Φ耦合势收敛曲线如图6所示。从图6可知，双旋度结构的A-Φ耦合势迭代3000次未达到预设的求解精度，而拉普拉斯结构的A-Φ耦合势经迭代2400次即达到预设精度。虽然前者得到的垂直磁场Hz与解析解吻合较好，但求解的迭代次数较多。对比分析表明，本文开发的三种CSEM求解方程算法准确，结果可靠。

图5 100Hz磁场Hz的实部(上)和虚部(下)响应曲线

图6 100Hz磁场Hz的收敛曲线

2.1.2 求解系统特点分析

为了分析三种CSEM求解方程的特点，仍然采用上节的均匀半空间地电模型。沿x方向、在地面放置一个电偶源，源长度为1m，发射电流为1A，发射频率为10Hz。求解区域的大小为[-30km,30km]3，分别采用前述三种求解方程对该模型进行求解，地面上各场分量等值线图见图7～图9。

由图7～图9可以看出，基于双旋度结构的A-Φ耦合势计算的矢量和标量位无明显规律，基于拉普拉斯结构的A-Φ耦合势计算的矢量和标量位特征符合预期。通过两种A-Φ耦合势计算的电场Ex等值线与基于电场方程计算的电场Ex等值线具有高度一致性，表明矢量基函数离散的矢量位A违背了连续性条件，导致矢量位A切向不连续，使得计算得到的矢量和标量位无明显规律，影响其收敛性。

图7 均匀半空间模型基于双旋度结构的A-Φ耦合势矢量位A各分量及电场分量Ex平面等值线图

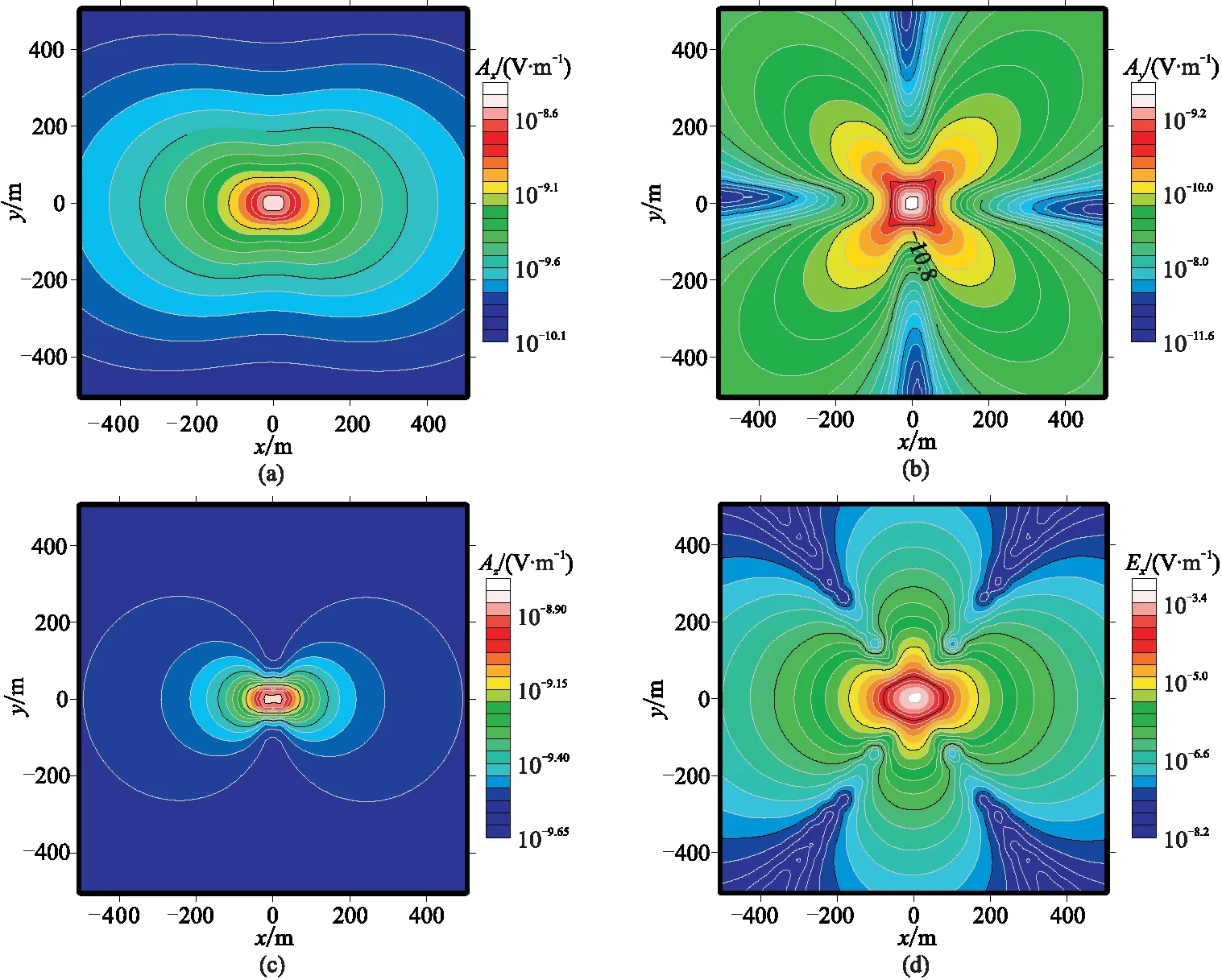
图8 均匀半空间模型基于拉普拉斯结构的A-Φ耦合势矢量位A各分量及电场分量Ex平面等值线图

图9 均匀半空间模型基于电场方程求解的电场E和磁场H各分量平面等值线分布

2.2 模型2：低阻模型

图10 低阻模型剖面(左)及模型剖分方案(右)

图11 低阻模型基于三种求解系统得到的3Hz电磁场分量实部(左)和虚部(右)对比

图12 低阻模型基于三种求解系统得到的10Hz电磁场分量实部(左)和虚部(右)对比

3Hz所对应的基于三种求解系统的不同求解器以及预条件因子的收敛性能统计结果见表1。由表可知，基于电场方程的CSEM矢量有限元方程在常规迭代求解器和预条件因子下均不能得到满意的计算结果。在同等精度、迭代求解器条件下，基于拉普拉斯结构的A-Φ耦合势CSEM求解方程收敛性总体上优于基于电场方程和双旋度结构的A-Φ耦合势方程。对于同一种求解方程，GMRES和BICGSTAB迭代求解器的求解效果相差不大。除此之外，GMRES和BICGSTAB迭代求解器结合SOR(超松弛)预条件因子对两种结构的A-Φ耦合势CSEM求解方程进行求解，收敛性差异不明显；而GMRES和BICGSTAB迭代求解器结合其他预条件因子进行求解的收敛性明显变差，所需迭代次数明显增加。这说明选择合适的预条件因子可提高方程组的求解效率。

表1 3Hz时三种求解系统、不同求解器及预条件因子的求解收敛性能对比

表2是不同求解方程/求解器组合下CSEM求解内存消耗、求解时间、迭代次数及相对残差的统计。对于方程组未知数在百万级以内的情况来说，直接求解器求解电场方程的优势明显，小型计算机即可满足内存需求；若需求解的未知数超过100万，计算机内存需求则超过15GB；当需求解的未知数继续增加，利用直接求解器求解线性方程组的计算机内存需求则难以满足。对于A-Φ耦合势求解方程，当未知数超过100万，内存需求不超过6GB，即A-Φ耦合势方程的迭代解法在内存需求方面的优势非常明显。但是，在时间消耗方面，对于未知数不超过100万的方程组求解，直接求解器相比迭代求解器优势更明显。

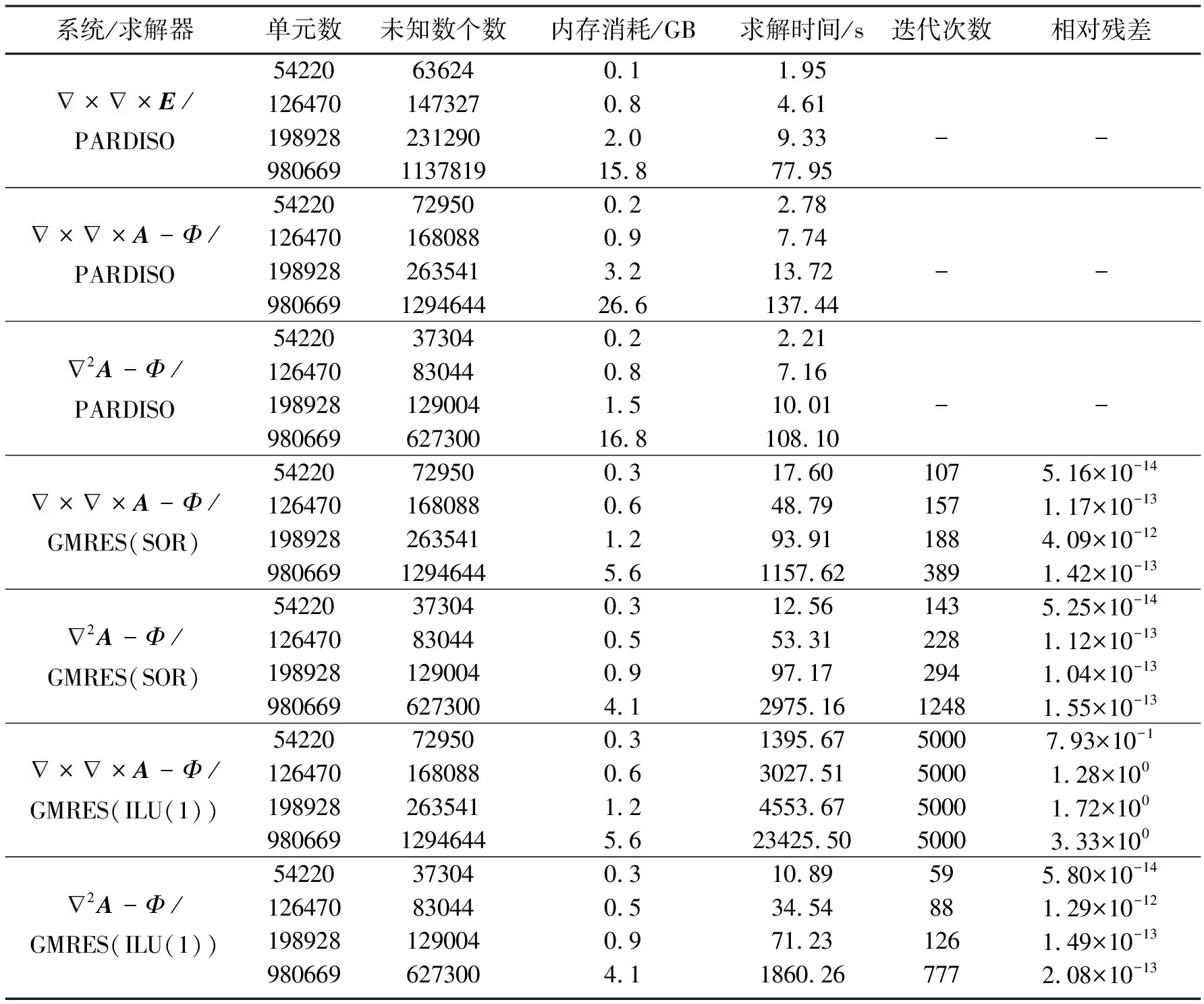
表2 三种求解系统相关技术性能对比

3 结论

本文采用非结构化网格对求解区域进行离散，实现了三种求解系统的CSEM正演计算。建立均匀半空间模型和低阻异常体地电模型，从计算精度、效率以及内存消耗三个方面分析基于两种A-Φ耦合势方程和电场方程正演问题的求解特性。得出以下几点认识。

(1)本文开发的三种正演求解算法程序准确且计算精度较高，采用的统一场源处理技术能够较好地扩展场源的适用性，同时结合局部网格加密技术可有效降低场源奇异性问题。

(2)在同等条件下，基于非结构网格的矢量有限元电场方程不适合于采用常规的Krylov子空间算法进行方程组的求解；相比于双旋度结构，基于拉普拉斯结构的A-Φ耦合势更适合于电磁场的迭代求解，其适用性更强。

(3)相比于A-Φ耦合势方程，基于电场方程的直接解法在方程组未知数不高于100万时，在内存需求和求解效率方面具有明显的优势；但是，若方程组未知数超过100万级，相比直接解法，A-Φ耦合势方程迭代算法在内存需求方面优势更明显。另外，若网格密度增加，常规的Krylov子空间迭代算法求解大型方程组所需要的时间成本会逐渐增加。

总之，本文系统对比了三种频率域CSEM正演求解系统，并对正演模拟的内存需求及效率进行了探讨。对于小尺度三维CSEM正演问题，电场方程的直接解法能满足需求；对于超大尺度三维CSEM正演问题，需要借助迭代算法开展线性方程组求解。