钢筋混凝土楼板高温动力损伤识别试验研究及非线性分析

辛春晓 高立堂 许业清

（青岛理工大学土木工程学院，青岛266033）

0 引 言

建筑结构在发生火灾时，结构的性能会发生变化，从而影响结构的正常使用功能，为了保证建筑结构的正常使用功能，需要对火灾后结构构件的状态进行有效判定。而基于动态特性的损伤识别方法在桥梁检测中取得一定成果，如何能更好地把其运用到火灾后建筑检测，对结构的损伤鉴定从定性到定量的转变，是我们的一大突破点。本文主要采用此方法对火灾下板的火灾后板的损伤深度、频率损伤进行定量的分析。

1 火灾试验研究

1.1 试件制作

本试验采用h/l＜1/6［2-3］的薄板，把平板振动的弹性体三维问题简化为二维问题。采用的薄板小挠度理论对试验进行理论分析。

共设计5块钢筋混凝土双向板。对钢筋混凝土板的板厚、配筋率、配筋间距等不同方面进行研究。其中，钢筋混凝土板截面设计尺寸为2 000 mm ×1 200 mm，混凝土采用强度等级为C30，混凝土立方体试块抗压强度34.2 MPa，混凝土保护层厚度为15 mm。从板的承载能力和经济性等多方面综合考虑分析，采用单层双向配筋的配筋方式。受力钢筋采用三级带肋筋（HRB400），直径为12 mm，分布钢筋采用三级带肋筋（HRB400），直径为10 mm。试件设计一览表如表1所示。

表1 试件设计一览表Table 1 List of test piece designs

1.2 试验方案

本试验在青岛理工大学结构试验室水平火灾试验炉完成，依据《建筑结构荷载规范》（GB 50009—2012）［4］，对板进行火灾试，在板上布置均布活荷载2.0 kN/m2，试验采用质量为25 kg的铁质砝码进行等效加载。分别沿板纵向、横向中间位置布置位计，以便测量钢筋混凝土板平面内和平面外变形，加载及位移计布置如图1所示。

图1 加载及位移计布置图Fig.1 Loading and displacement

在对炉内温度进行数据采集时，需在板四边中间靠近板底部直接受火处，布置4 个N 型热电偶［5］，这样保证测点温度能更好地反映炉内温度，如图2所示。

图2 板厚方向温度测点示意图Fig.2 Schematic diagram of temperature measurement points in the thickness directio

1.3 温度场采集与分析

通过Agilent34980A 温度采集仪对测得炉内和板内温度数据进行整理分析，绘制的炉内（板）温度与随时间变化曲线标准如图3所示。

通过图3（a）试验炉内温度，可以看出火灾炉内的温度变化趋势与ISO834 标准升温曲线基本一致。通过图3（b）板的温度数据分析：混凝土在加热100 ℃左右时，有一平缓台阶，出现这一现象的主要由于板在升温过程中，混凝土中的水分的迁移以及自由水以水蒸汽的形式从板中蒸发，吸收热量，导致混凝土的温度难以升高；楼板内部温度随时间增加逐渐升高，且呈非线性变化，混凝土材料的热惰性导致温度这种非线性增长。在受火60 min 时，楼板底面最高温度达到852 ℃，最低温度达到718℃；楼板上表面最高温度达到137 ℃，最低温度达到63 ℃。一般采用隔热破坏准则，即板顶平均温度达到140 ℃，最高温度达到180 ℃，板会发生破坏。受火60 min，板底温度超过800 ℃，板顶还没达到破坏温度，水分的蒸发带走了大部分热量。显而易见，在进行温度场分析时，考虑水分的蒸发尤为重要。

图3 板内温度测点图Fig.3 Temperature measurement points in the board

1.4 楼板高温损伤深度分析

高温会使钢筋和混凝土的材料性能发生劣化，而弹性模量随着温度的升高，呈现非线性降低。根据有关文献［3］，当混凝土温度到达300 ℃弹性模量变为常温时的0.7 倍左右；到达500 ℃时［11］，弹性模量变为常温的0.45 倍左右，把300 ℃和500 ℃分别作为轻度损伤和高度损伤界限。

在试验数据的基础上，分析各试验板进入轻度损伤深度与重度损伤深度所需要的时间，如表2所示。

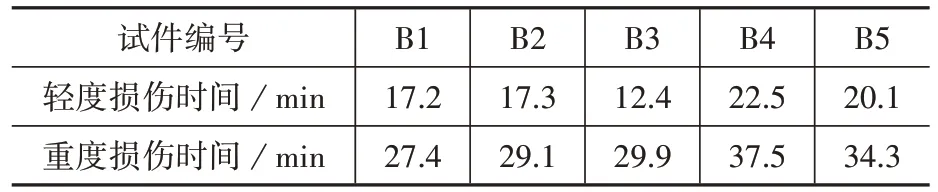
表2 测点达到相应损伤深度时间表Table 2 Timetable for measuring points to reach the corresponding damage depth

通过线性差值计算，分析各试验板的损伤深度。插值计算公式为

式中：t1表示达到轻度损伤或重度损伤的该测点温度所对应的温度值；t代表轻度损伤温度值300 ℃或重度损伤温度值500 ℃；t2表示第一个未达到轻度损伤或重度损伤的该测点温度所对应的温度值；h代表楼板厚度；d表示达到轻度损伤或重损伤的该测点到楼板底部的高度值。

计算结果如表3所示。

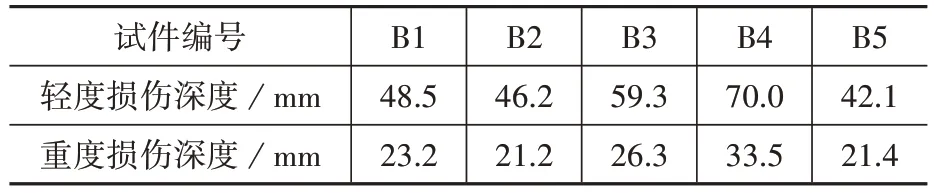
表3 高温损伤深度表Table 3 Depth of high temperature damage

通过表2 分析可知，楼板底部温度在平均时间16.56 min 达到轻度损伤阶段，平均时间31.86 min 达到重度损伤阶段；由表3 分析可知，B1～B5试验楼板在遭受高温作用后达到轻度损伤的深度所占的比例分别为48.54%、46.20%、49.41%、46.67%、42.12%，重度损伤深度所占的比例分别为23.20%、21.24%、21.93%、22.10%、21.42%。经过1 h 的高温，板的损伤就超过40%，随着高温时间的增加，损伤深度还会继续增加，因此，火灾时间和温度对火灾后板的损伤评估有很大影响。

2 结构动力试验分析

2.1 支座设置

本试验是对火灾后的板，进行四边简支和四边固支的动力试验，根据混凝土结构试验方法标准［5-6］，试验采用直径为 100 mm 的钢球和直径100 mm、长度150 mm 的钢辊轴作为试验板的支座，且四边支撑板滚珠间距宜板在支撑处板厚度的3～5倍，支撑方式布置见图4。

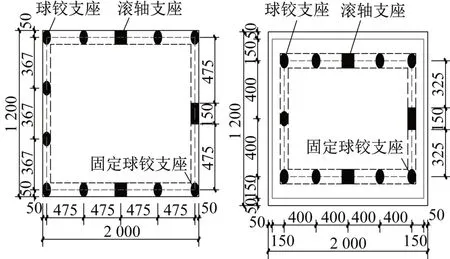
图4 支座布置图Fig.4 Support layout

2.2 传感器布置

本试验模态测试采用单点激励-多点响应的方式，将板沿长度和宽度方向划分为4份共5个测点，具体尺寸见图5。

图5 传感器布置图（单位：mm）Fig.5 Sensor layout（Unit：mm）

2.3 动力试验过程

在进行动力实验时，通过LMS Scadas Mobile多通道数采前端和高性能E系列输入模块进行数据采集［7］。

试验中，首先，启动LMS，进入模态分析界面，创建文件并将其命名。根据试件尺寸建立几何模型，将实际坐标赋予笛卡尔坐标系中，设置力锤通道并将其作为参考通道，并对传感器类型和灵敏度进行设定，为每个通道分配相应的测量点和振动方向，几何模型如图6所示。

图6 试验布置图Fig.6 Test layout

进入测量（Measure）界面进行锤击法模态测试，锤击时，把握力度和速度，每个点测试三次。在选取试验数据时，使用 polyMAX 方法［8］对测量数据进行模态分析，把稳态图峰值附近“s”状态较多的极点作为模态阶次，即频率、阻尼和矢量稳定在容差范围内的极点，并根据模态振型进行综合选择，如图7所示。

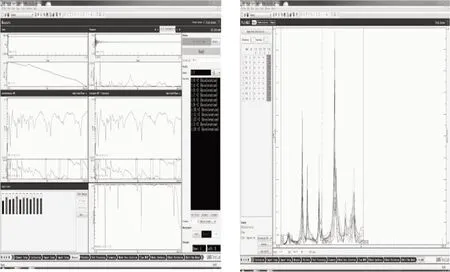
图7 模态分析图Fig.7 Modal analysis diagram

2.4 阵型分析

本试验模态采集使用LMS Scadas Mobile［11］多通道数采前端和高性能E 系列输入模块。使用LMS Test.Lab分析软件中的模态分析（Impact Testing）进行模态分析。单点激励多点响应方法适合低频，本试验主要针对四边简支双向板和四边固支双向板前两阶频率进行分析，并绘制阵型图。

2.4.1 四边简支板高温后振型

m，n分别为振型沿x，y方向的半波数，根据固有频率公式可知，（m，n）数值越大，频率越高。若x向长（a值较大），则x向半波数较多时频率不高，而在y向有相同半波数时频率较高，也就是依频率大小次序，x向（长向）先出现多节载；对于同样阶次，随长宽比增加，频率系数增加，对于同样（m，n）数，也随长宽比增加而频率系数增加。一阶振型在x，y方向各为1个半波、二阶振型在x方向2个半波，y方向1个半波。根据经验和理论分析，选择合理的数据，来选取合适的阵型图如图8所示。

图8 四边简支阵型图Fig.8 Four-sided simple support formation

2.4.2 四边固支板高温后振型

通过文献［3］可知，四边固支板的基本振型方程式与四边简支板基本相同，不同的是边界条件，本文根据边界条件求解方程。首先引入待定系数Aij，然后求解四边固支板的振型是x方向为i个半波，y方向为j个半波的振型乘Aij的组合，绘制如图9所示的阵型。

图9 四边固支阵型图Fig.9 Four-sided fixed support pattern

通过动力测试及理论分析，高温前后楼板振型基本保持一致性。因为试验炉内均匀受火且试验板的一维热传导方式，使得板面损伤呈现近似梯形。

2.5 动力分析

在对动力参数进行选取时，一般选择相频图中相位在 0°或者±180°［9］附近上会出现比较明显的峰值，而且同时在该频率处相干函数曲线值大于0.95。试验过程中，满足以上条件且重复次数比较多数据，一般重复三次取值相同时，才确定该峰值点所对应得频率即为所得固有频率值。试验各楼板动力测试及理论结果对比见表4。

表4 动力测试与理论结果频率对比表Table 4 Frequency comparison table between dynamic test and theoretical results

通过表4 中数据可以看出：四边简支双向板的理论计算基本频率与试验实际测量数据基本吻合，其中B1～B5 试验实际测量的基本频率相对于理论计算的基本频率普遍偏低，分别偏低11.62%、8.54%、12.94%、13.57%、13.65%，偏差符合试验允许范围。从而进一步说明四边简支边界约束条件符合要求；其频率随着配筋率和板厚的增加而增加，随着加热时间的不断升高，基频和二阶频率都出现非线性的降低的趋势，这种趋势的主要原因是高温导致材料性能发生不同程度的破坏。

为了更好地观察高温前后频率的变化，根据数据绘制表格，如表5所示。

表5 高温前后频率比值表Table 5 Frequency ratio table before and after high temperature

从频率对比表中可以看出：配筋率和板厚影响高温频率的衰减，随着配筋率和板厚的增加，这种衰减呈现不断减小的趋势。

2.6 非线性分析

本文采用经典震动理论和名特林板理论进行分析，对高温后的钢筋混凝土板沿厚度方向划分温度带，认为同一温度带板在任意方向的材料性能相同，上下层板块之间的材料性能沿厚度方向随温度梯度呈非线性变化。即假设为横观各向同性板。

采用四边形等参单元的方法进行分析，总体坐标体系xoy 和局部坐标体系ξoη相结合，且边界条件为ξ=±1、η=±1。

在同一温度带内，截取矩形单元进行分析，如图10所示。

图10 矩形单元Fig.10

设结点位移向量：

结点力向量：

单元在x，y，z方向的线位移为

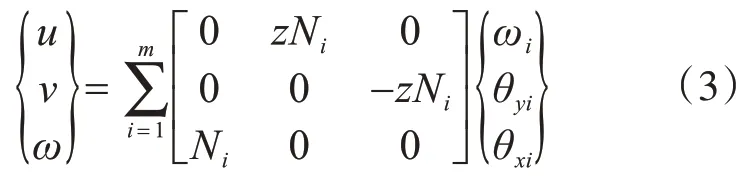
运用几何关系可得应变分量：

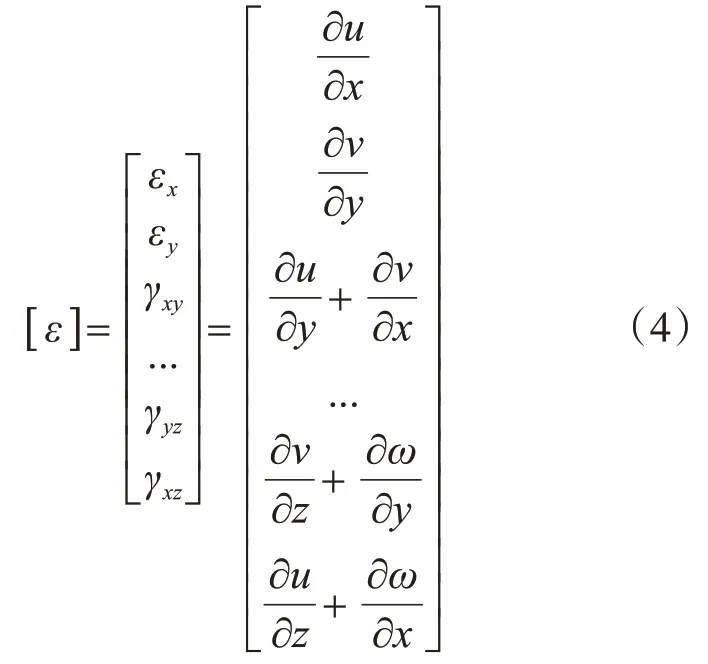
在分析计算中引入高温下混凝土弹性模量与温度的关系：

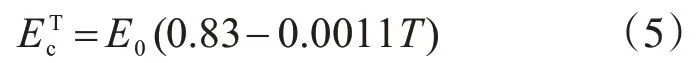
由虚功原理，可得单元节点力：

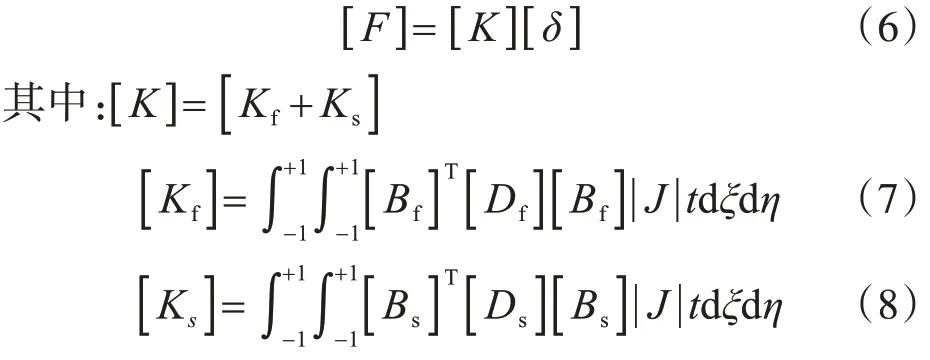
式中：t为单元厚度；|J|为雅可比矩阵。

对上式采用2×2个高斯积分点求解：

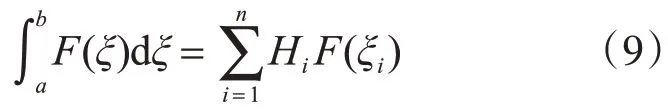
在对高温后钢筋混凝土板进行分析时，考虑热力耦合作用，即钢筋和混凝土本构模型。

为了计算简洁采用，本文主要采用逐步增量法中的等刚度迭代进行求解。根据平衡条件：

式中，[KT]为整体刚度矩阵，由单元刚度矩阵按着标准方法集合而成。

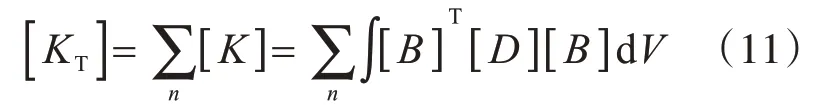
在材料处于弹性阶段或进入非线性时，［D］分别取对应状态下的值。

使用初始刚度[K0]求出位移近似值：

根据求解出的[δ1]求出单元应变[ε1]，再根据应力应变关系求解单元应力[σ1]。由[σ1]求解节点力：

将[ΔP1]加载到结构上，根据[K0]求得附加位移增量：

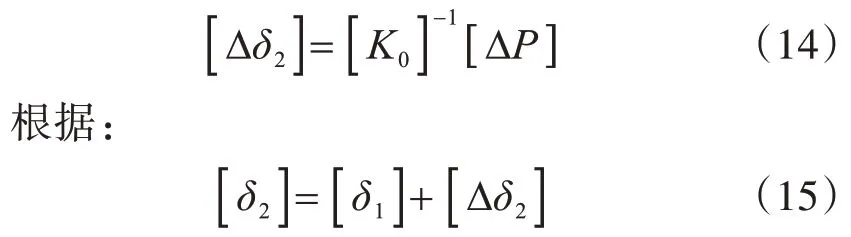
重复上面的步骤，直至确定一个收敛准则，即范数α。根据文献［12］，对于钢筋混凝土结构，取α=1%～3%即可满足精度要求。

根据达朗培尔（DAlember）原理，建立动力学方程，并得到动力平衡方程：

其中，［M］称为整体质量矩阵，它是由各单元的质量阵矩［m］集合而成，其集合的规则与刚度矩阵［K］相同。［Q］是等效结点载荷矢量。

式中，Me，Ke，Qe分别为单元的质量矩阵、刚度矩阵和荷载向量。

在对单元质量矩阵求解时，将其转换为单元集中质量矩阵。求解方法如下：

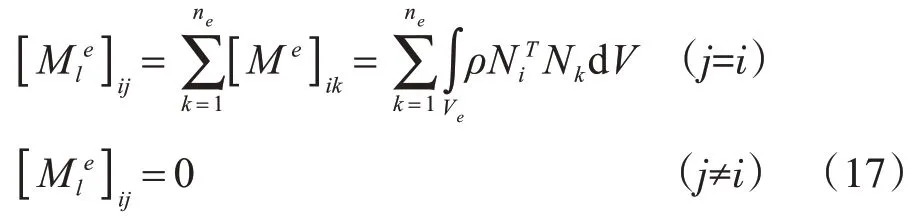
在进行动力特性分析时，系统的自由度很多，对于板而言，在研究系统的响应时，往往只需要了解少数较低的特征值及相应的特征向量。由于本试验是计算前两阶频率值，采用反迭代法进行频率、阵型求解。

2.7 Fortran语言编程求解分析

根据以上分析，利用Fortran90 语言编程求解高温后四边固支钢筋混凝土板的频率、振型，编程求解与试验结果对比如表6所示。

表6 高温后四边固支板频率值的试验结果与程序结果Table 6 Test results and program results of frequency values of four-sided clamped plate after high temperature Hz

为了更加直观的观察，配筋率和板厚对高温后板的四边固支频率的影响，以及试验与程序求解出来的频率就行比较，对以上数据进行如图11、图12所示绘制。

图11 试验值与程序值一阶频率对比图Fig.11 First-order frequency comparison between test value and program value

图12 试验值与程序值二阶频率对比图Fig.12 Second-order frequency comparison between test value and program value

由试验测取结果与程序计算结果分析发现，两者的结果吻合性较好。其中B1～B5 的一阶固有频率偏差分别为 10.38 Hz、29.79 Hz、20.80 Hz、11.28 Hz、22.13 Hz；二阶固有频率偏差分别为10.14 Hz、26.02 Hz、19.87 Hz、3.52 Hz、23.14 Hz；也说明了本程序的可靠性，计算准确性可以满足工程实际。从试验数据和程序数据对比发现：一阶程序数据普遍高于试验数据，二阶程序数据和试验数据在上下波动。造成这种现象的主要原因有以下两点：①程序编写时没考虑裂缝等因素，裂缝的产生和发展会对频率产生影响；②混凝土的热惰性、弹性模量与高温关系等相关参数是由于相关文献试验获取的本身就有一定程度的离散型。

高温的作用使得钢筋混凝土板的材料性能发生一定程度的劣化，引起钢筋混凝土板的截面抗弯刚度的非线性下降趋势，最终的结果是体现在结构板动力特性固有频率的下降。

3 结 论

（1）通过火灾下钢筋混凝土板的试验结果分析得出：楼板在平均受火16.56 min 达到了轻度损伤；31.86 min 达到了重度损伤。B1～B5 试验板在持续60 min 的火灾作用下，轻度损伤深度占楼板厚度在42.37%～49.50%，重度损伤深度占楼板厚度在21.26%～23.29%，随着时间增加损伤还不断加剧。

（2）通过高温前后板的频率试验数据对比分析可知：高温会使钢筋混凝土板的频率衰减，基本频率衰减超过50%，二阶频率比一阶频率多衰减1%～6%，配筋率和板厚会影响频率衰减，配筋率和板厚越大衰减越小，而且随着时间增加，这种衰减趋势越明显，呈现非线性变化趋势。

（3）利用Fortran90 语言编写程序进行求解，获得数据与试验测取结果进行对比分析发现，一阶频率偏差在10～50 Hz，二阶频率偏差在10～30 Hz，更好地说明了程序和试验数据得到了很好的吻合，也进一步阐释了高温损伤的实质是对材料非线性的影响。