基于ECMWF集合预报的海河流域降水概率预报应用和检验

徐姝，熊明明，陈法敬

(1.天津市气象台，天津 300074；2.天津市气候中心，天津 300074；3.国家气象中心，北京 100081)

引言

大气是一个混沌系统，天气预报的不确定性是其根本属性之一(叶笃正等，2006)，预报不确定性通常用概率方式来表达(王东海等，2011)。概率天气预报的任务，是要为预报产品使用者提供预报制作者对天气状况未来发展趋势认知状态的较完整表达；其中，很重要的一点就是对预报不确定性的定量化表达。同确定性预报相比，概率预报可提供更加丰富的预报信息(俞小鼎等，2004；李俊，2015)。集合预报是由单一确定论向多值随机论转换的关键技术(王晨稀和姚建群，2008；杜钧和邓国，2010；杜钧和陈静，2010；杜钧和李俊，2014)。集合预报方法产生之前，概率预报通常是通过统计方法得到的(Wilks，2005)，但统计概率预报只反映过去出现过的天气状态。常规统计方法可减小系统性误差，但对随机性误差无可奈何，集合预报虽能消除随天气系统变化带来的随机性误差，其各成员分别表征一种可能的天气状况，预报的不确定性可采用各成员的概率密度来体现，实现更具有动力学意义的概率预报(Stephenson et al.，2005)，但历史预报资料中的集合预报性能信息没有得到有效利用。贝叶斯概率预报方法可融合历史资料和集合预报系统生成的数据，给出连续的概率预报曲线，受到集合预报应用方面的重点关注。在气象领域，马培迎(1999)较早地应用贝叶斯原理，将天气分为有、无降水，以其期望概率作为先验概率，对降水概率预报进行修正，提高了降水预报精度。陈朝平等(2010)利用贝叶斯公式求得暴雨的后验分布，并建立了四川境内147 个站点的暴雨预警模型。陈法敬等(2011)将地面气温作为预报量，利用BPO(Bayesian Processor of Output)方法，将单一集合成员预报转化为概率预报，得到预报效果优于单一成员的集成贝叶斯概率预报。刘建国等(2013)利用TIGGE 构成的多中心超级集合系统，结合淮河流域地面观测建立贝叶斯模型平均(Bayesian Model Average，BMA)概率预报模型，获得的地面日均气温概率预报比原始集合预报效果好。韩焱红等(2013)通过分别对广州、武汉、南京、成都和北京集合预报成员建立贝叶斯产品处理技术降水概率预报模型，发现其可靠性高于基于集合预报生成的直接概率预报结果。张宇彤等(2013)基于贝叶斯原理和贝叶斯降水概率预报模型，使用中国T213全球集合预报历史资料作为先验信息，对中国不同气候区代表站建立贝叶斯降水概率预报模型，对预报结果有一定改进。石岚等(2017)利用ECMWF将BMA概率预报模型与确定性数值模式预报进行融合，对风能预测产品具有明显改进。

上述研究表明，应用贝叶斯概率预报方法提取模式产品有效信息对预报量的气候(先验)概率进行修正，得到模式预报与气候概率最佳融合的预报信息可提高预报准确率，但先前贝叶斯产品处理技术的研究主要在做方法的探索，试验大都只是针对单站，并且试验时段较短,难以客观全面地反映贝叶斯预报的效果，特别是缺乏空间分布上面的表现。随着智能网格预报业务在气象领域的深入推广，急需开展基于网格降水概率预报的应用研究，相比于站点试验仅能获得固定站点位置的信息，格点化研究，可以为覆盖的范围提供所有位置上概率预报信息，丰富扩展了该方法可以提供改进信息的空间范围。本文利用海河流域范围内降水实况和ECMWF 集合预报数据，采用BPO的方法(Krzysztofowicz，1999；Krzysztofowicz et al.，2001)对流域内289 个格点建立降水概率预报模型，根据预报能力对模式51 个集合成员进行贝叶斯降水概率预报信息融合，从而生成集成的海河流域贝叶斯降水概率预报产品，采用RPS 和BS 评分方法检验其在2018年汛期的预报效果，为概率预报在业务中的应用提供有益的指导。

1 方法与资料

1.1 方法

贝叶斯方法的核心是贝叶斯公式，即

上式表达了根据已有的经验推断一个先验概率P(Y)，然后在新信息或者说似然模型P(X|Y)的更新下不断地重新调整先验概率，进而得到事件发生的后验概率P(Y|X)的过程。

BPO 方法(韩焱红等，2013)是通过建立数值模式预报的概率化模型，把确定性预报量转变为概率预报，通过概率来定量化地表达模式预报值的不确定性。对降水而言，总体可分为有无两种情况，而在降水发生后，降水量则变成了一个连续型的气象要素。BPO方法的降水概率预报模型如式(2)或(3)所示，公式表明概率预报由两部分构成：无降水的概率和条件降水量的概率分布，其中x 为降水预报因子，y为预报量，π 表示有降水的后验概率，Φ()y和φ(y)分别表示了条件降水量的后验概率分布和后验密度函数，δ为狄拉克函数。其概率分布形式为

由式(4)得到有降水的后验概率π，其中g为有降水的先验概率(降水阈值为0.1mm)，可由历史降水观测数据统计得到。f0、f1分别为无和有降水时的条件密度函数，代表预报因子和预报量之间的随机相关性。

后验概率分布Φ(y)和后验概率密度φ(y)由式(5)、(6)计算得到。其概率分布函数形式为

其中，Q为标准正态分布函数；G(y)、K(x)是降水历史观测值和预报值估计得到的条件降水量y的先验概率分布、预报因子x的边缘分布，本文采用威布尔函数估计G(y)和K(x)，即

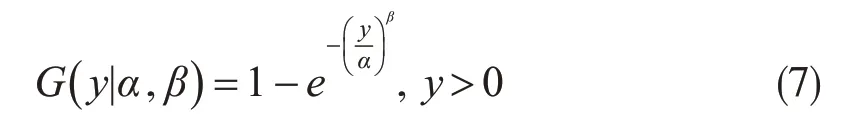
由于降水这一要素不符合高斯分布随机依赖结构，但符合亚高斯结构，因此这里采用Kelly 等(1995)和Krzysztofowicz(1997；2008)提出的亚高斯似然模型，即在正态-线性似然模型的基础上，引入正态分位数转换(Normal Quantile Transform，NQT)，得到亚高斯似然模型，正态分位数转换表示为

Q-1代表标准正态分布函数的逆，转换后的变量符合标准正态分布。c1，c0，T 表示BPO 预报模型中的后验参数，；其中a、b、σ是似然参数，由正态分布变量u、z 的均值μ0、μ1，方差以及协方差σ10通过公式得到。

1.2 资料

本文选取海河流域范围内(111°—120°E，34.5°—43°N)289个格点进行试验(图1)。将集合预报中单一集合成员24 h 降水预报值作为预报因子x，格点24 h降水量作为预报量y。

图1 海河流域国家气象站、ECMWF集合预报格点、代表格点1和2分布图Fig.1 Distribution of precipitation observation stations,ECMWF ensemble forecast grid points and the representative grid 1 and 2 in Haihe River Basin.

由海河流域1961—2018 年6—8 月国家气象观测站逐日20—20 时24 h 降水观测资料，采用最邻近法，插值到邻近格点上，并计算得到各格点的降水先验概率。为研究BPO方法在集合预报中的应用，本文预报因子x 选取ECMWF 集合预报逐日预报的海河流域格点预报资料，试验时段为2012—2018年6—8月期间，其中2012—2017 年为模型建立样本，采用2018 年样本进行验证。

2 建立基于单一预报成员的贝叶斯概率预报模型

2.1 正态分位数转换

以格点1、格点2为例，图2a、c表示降水量的控制预报与观测值的随机依赖结构，散点分布图为联合样本x与y的分布形式，可见降水分布特征不服从标准正态分布。图2b、d中散点是预报量y和预报因子x经过NQT转换后的u和v的分布形式，红线为y经NQT转换后的变量u的概率密度曲线，蓝线为x经NQT转换后变量z的概率密度曲线，可见，转换后的变量均符合正态分布。

图2 降水观测值y与预报值x(a.格点1；c.格点2)散点分布图和NQT转换量u、z(b.格点1；d.格点2)的标准正态分布Q-1(G(y))及Q-1(K(x))Fig.2 The scatter plots of predict and y and predictor x of(a)grid 1 and(c)grid 2,and the standard normal distribution of NQT transformed u and z of(b)grid 1 and(d)grid 2.

2.2 单一集合成员降水概率预报结果分析

基于ECMWF 集合预报控制预报，将转换后的先验分布和预报值的边缘分布函数带入公式(2)、(3)，建立流域内格点2018年6—8月逐24 h降水BPO概率预报模型，进而生成流域内各格点逐24 h的降水概率分布(或概率密度)预报。

由BPO 模型计算获得289 个格点的6—8 月逐日有降水的后验概率πk。这里选取格点1和格点2作为代表，将通过BPO建模修订得到的后验概率πk与直接由历史观测资料统计得到的先验概率gk进行比较(图3)，从中看出，后验概率πk较先验概率gk逐日变化起伏更加明显，说明将模式预报作为预报因子提供的有效信息发挥了一定修订作用。

图3 格点1(a)、格点2(b)的6—8月逐日有降水先验概率(gk)与后验概率(πk)Fig.3 The prior probability of precipitation occurrence gk and posterior probability πk of each day from June to August at(a)grid 1 and(b)grid 2.

以ECMWF 对格点1 和格点2 的2018 年7 月24 日降水预报为例，得到基于ECMWF 单一集合成员的贝叶斯概率化降水概率预报显示，格点1 的观测值为117 mm，ECMWF 控制预报为49.6 mm，修订后概率密度最大值为60 mm，与确定性预报相比，预报准确性有所提高(图4b)；格点2 的观测值为0.4 mm，ECMWF 控制预报为7.3 mm，修订后概率密度最大值为1 mm，与观测值更接近(图4d)。可见，相比确定性降水预报，贝叶斯概率预报给出更多预报信息，且以概率的形式连续、定量化给出降水预报不确定性(韩焱红等，2013)。

图4 贝叶斯与气候降水概率预报结果对比:(a)基于ECMWF控制预报对格点1的2018年7月24日降水预报得到的概率分布预报；(b)同(a)，但为概率密度预报；(c)基于ECMWF控制预报对格点2的2018年7月24日降水预报得到的概率分布预报；(d)同(c)，但为概率密度预报Fig.4 Comparisons of Bayesian forecast and climate forecast based on deterministic prediction.(a)Cumulative probability prediction taking ECMWF precipitation forecast on 24 July 2018 at grid 1 for example,and(b)the same as(a)but for probability density.(c)Cumulative probability prediction taking ECMWF precipitation forecast on 24 July 2018 at grid 2 for example,and(d)the same as(c)but for probability density.

3 集合预报各成员的集成降水概率预报模型

由上文分析可知，通过贝叶斯方法可以将EC⁃MWF集合预报的一个成员转化为概率预报形式，EC⁃MWF 集合预报有51 个成员，对应有51 个贝叶斯概率预报，各成员的概率分布各不相同，预报效果存在差异，需要有一种合理的方法将所有成员的预报能力差异性或者说不确定信息定量地表现出来。

Krzysztofowicz(1992)提出了表征预报因子有效信息的评分方法(Informativeness Score,IS)，即

IS值越大，表示预报因子中有效信息越多，该成员的预报技巧越高，其值在0～1 之间。2018 年7 月24 日这次过程为例，基于ECMWF 集合预报成员对格点1的24,48,…,216,240 h 的降水预报值建立亚高斯似然模型，得到各集合预报成员的IS 值，结果如图5a 所示。不同时效内，24 h降水预报得到的IS 值明显高于240 h；对于24 h 预报，各成员中集合成员20 的预报能力最优，集合成员5 最弱，其对应的IS 值为0.71 和0.56。可见，IS 值能较好地表征不同集合成员所含有效预报信息的差异。进而，采用正比于IS3的值作为权重系数来体现各集合成员在所有成员中预报价值的差异。

其中，min函数用于计算各集合成员IS3的最小值，n为所有集合成员的数量。通过式(10)融合ECMWF的51个成员的IS值，得到各集合成员的24 h权重系数(图5b)。

权重系数同IS值的变化一致，集合成员20的24 h预报效果最好，故其权重系数也最大(0.039)；同理，集合成员5 的24 h 预报效果最差，其权重系数为0 (图5b)，权重系数可较好地表征各集合成员在融合预报结果中的地位。因此，可通过权重系数ri(ISi)参考式(11)的计算方法对集合成员的概率预报信息进行归一化加权平均，从而得到融合后概率密度预报结果。概率分布预报结果，进一步由式(12)对概率密度函数积分得到。

图5 基于ECMWF集合预报对格点1降水预报得到的IS值(a)和权重系数r(ISi)(b)Fig.5 The(a)IS and(b) r(ISi) obtained based on ECMWF ensemble forecast for grid 1.

4 集成贝叶斯降水概率预报结果分析和检验

4.1 应用检验

分别采用RPS和BS评分，以模式区域内289个格点的24 h降水概率预报结果作为统计对象，对试验结果进行评价。

RPS评分是一个对所有降水量级的概率预报结果综合评价与衡量的量度，RPS 值在0～1 范围内，且其越小越好。从图6中看到，对于2018年6—8月每天的降水情况，格点的集成贝叶斯降水概率预报综合效果比集合直接概率预报要好，尤其是“七下八上”华北主汛期；另外，对于48 h和72 h预报时效，集成贝叶斯降水概率预报的可靠性较集合直接概率预报效果更加明显，随着预报时效增加，各个集合成员之间的离散度也随之增加，导致集合概率预报的不确定加大，而贝叶斯概率预报方法对历史数值预报信息的有效融合，所提供的预报因子有效信息对最终预报结果具有改进效果。

BS评分是对降水的某一个等级的概率预报结果评价的一个指标，在0～1的范围内，其值越小越好。图7给出了2018年6—8月各降水量级24 h、48 h和72 h降水概率预报的平均BS 评分情况，3个预报时效、5 个阈值中集成贝叶斯降水概率预报的BS 评分均低于集合直接概率预报，尤其是0.1 mm 和10 mm 两个阈值，分别减小了19%和31%，且随着时效的增加，集成贝叶斯降水概率预报较集合直接概率预报的优势更加明显，48 h的0.1 mm和10 mm的BS评分分别减小了35%和40%，72 h分别减小了35%和35%，这与RPS评分效果一致。从图7 结果还可看到，对于25 mm 以上降水量级的BS评分明显降低，这与统计方法有关，并非降水量级越大概率预报效果越好。由于参评格点数不变，而降水范围是变化的，导致25 mm 以下降水范围总比25 mm以上降水范围大，而降水区域大的要比区域小的BS 评分大，不同量级降水的BS 评分不具可比性(王晨稀，2005)。

图7 2018年6—8月海河流域所有格点在不同降水阈值下24 h(a)、48 h(b)、72 h(c)集成贝叶斯降水概率预报与集合直接概率预报的BS评分Fig.7 The 24h(a),48h(b)and 72h(c)BS value of integration Bayesian precipitation probability forecast(Integrated Forecast)and ensemble direct probability forecast(Ensemble Forecast)on the grids based on ECMWF ensemble forecast under different precipitation thresholds from July to August in 2018.

4.2 强降水过程检验

为检验BPO 降水概率预报模型对智能网格预报业务支撑能力，评估该模型格点预报场的预报效果，选取2018 年7 月23 日一次强降水过程做试报检验。本次过程受台风“安比”影响，流域自南向北先后出现强降水，流域东部出现大到暴雨，滦河下游、北三河下游、大清河下游以及海河干流出现大暴雨。以2018年7月23日未来24h降水预报为例，首先对ECMWF各集合降水预报成员建立BPO概率模型，获得一组集合成员贝叶斯降水概率预报，然后根据式(6)和(7)对51个成员的概率预报进行融合，最终得到集成的贝叶斯降水概率预报(图8)，不同降水量级的高概率区(图8a—e)与实况(图8f)的分布基本一致。从表1也可看出，此次过程24 h的RPS和BS评分，集成贝叶斯降水概率预报均好于集合直接概率预报。

表1 24 h降水概率预报评分Table 1 Value of precipitation probability forecast for 24 h.

图8 海河流域2018年7月23日20时—24日20时小雨(a)、中雨(b)、大雨(c)、暴雨(d)、大暴雨(e)概率(单位:%)分布及实况降水(单位:mm)分布(f)Fig.8 Probability(unit:%)distributions of(a)light rain,(b)moderate rain,(c)heavy rain,(d)torrential rain,(e)downpour and(f)precipitation(unit:mm)distribution in Haihe River Basin from 20:00 BT 23 July to 20:00 BT 24 July 2018.

综上所述，基于ECMWF 集合预报对流域内格点2018 年逐日24 h 降水建立降水概率预报模型并采用RPS和BS评分检验。所得结果表明，格点的集成贝叶斯降水概率预报的预报效果优于集合直接概率预报，这种基于贝叶斯理论的集合降水概率预报方法适用于海河流域。

5 结论

将BPO 方法应用于海河流域进行降水量概率预报试验，动态建立了流域内基于ECMWF集合预报289个格点的BPO概率预报模型，并对其在研究区域的预报技巧进行评估。ECMWF集合预报每个集合成员性能存在差异，利用正比于IS3的值作为权重系数来体现不同集合成员的预报能力，进行各成员贝叶斯概率预报信息的融合，得到连续概率密度函数形式的集成贝叶斯概率预报。2018 年6—8 月及“安比”个例的RPS和BS评分检验结果，均表明集成贝叶斯降水概率预报效果优于集合直接概率预报，因此，贝叶斯降水概率预报方法可在海河流域网格概率降水预报业务中进行应用。

BPO概率预报给出的概率密度函数，将预报的不确定性定量化表达，通过概率密度函数的解释应用，可在一定程度上提高预报精度，使得对极端事件具有一定的预报能力，但仍有可能存在部分极端降水的漏报和空报。本文只选取数值预报模式的降水量预报作为预报因子，下一步工作还可以尝试采用多个预报因子，如：加入比湿、相对涡度等作为预报因子，利用它们构成的一个预报因子向量进行定量降水概率预报，从而得到更好的预报效果。