高烈度地震作用下多年冻土区既有路基动力响应特性分析

李合银

（中交二公局第四工程有限公司，甘肃 玉门 735200）

一、引言

目前，全球多年冻土区约占全球陆地总面积的25%，主要分布在俄罗斯、加拿大、美国和中国。我国多年冻土面积约占陆地总面积的22.4%，并且广泛分布在青藏高原、东北地区和西北山区。随着我国寒区经济建设的快速发展，越来越多的交通基础设施工程也开始如火如荼地建设，然而青藏高原附近有许多大而密集的地层活动断裂带，地震频繁—1980年至2006年期间，发生了186次Ms5.0级～5.9级地震，33次Ms6.0级～6.9级地震和3次Ms7.0级～8.5级地震。特别是2001年11月14日，在昆仑山西侧发生的一次8.1级地震，在冰冻的地面上造成了426公里长的破裂带，并摧毁了西藏公路的部分路堤。此外，2010年4月14日，青海省玉树县发生两次7.1级地震，对国道214线、省道308线和省道309线等公路路基基础设施造成了灾难性破坏，主要的破坏类型有差异沉降、起伏、错位和裂缝。总而言之，这些高强度地震严重威胁着多年冻土区公路路堤的可靠性和安全性。因此，研究高烈度地震作用下多年冻土地区路堤的动力响应特性具有重要意义。

目前，国内外学者已比较系统地分析了融土区的既有路基动力响应特性，对研究高烈度地震作用下多年冻土地区路堤的动力响应具有重要的参考价值。例如以山西大同某高速公路为依托，通过施加水平向及竖向的双向地震荷载，研究了路基不同部位、不同时间的地震动力响应，并对比分析了时程；设计并开展了比例为1∶20的大型振动台缩尺模型试验，研究分析了以软岩和石英砂为材料的路基模型，在不同地震波频谱特性及不同地震动荷载作用下不同部位的动力响应全过程损伤；基于GEO-SLOPE有限元软件中的SLOPE/W模块和QUAKE/W模块，系统地研究了路基结构在高烈度地震荷载作用下的动力稳定性，以及相关影响因素。然而，这些研究均较少针对竖向、水平地震波同时作用下的路基动力响应，且大多集中在融土区二维模型上而较少涉及冻土区三维模型。因此，研究高烈度地震作用下多年冻土区既有路基动力响应特性分析具有显著的理论意义和实践价值。

本文根据动力有限元微分方程，在有限元软件ABAQUS中建立了多年冻土区的路基三维地震动力有限元数值模型，研究了其不同季节时在水平地震波和竖向地震波作用下的动力响应。此外，为防止地震波在边界处反射和折射，还在该模型边界处施加了黏弹性边界，更好地实现了路基的动力响应模拟。

二、有限元模型建立

（一）动力有限元控制方程

如公式（1）和公式（2）所示，λ为常数；ε为土体积应变；t为时间；u、v、w分别为微六面体沿x、y、z正方向的位移分量；ρ为土层密度；G为剪切模量；E为弹性模量；μ为泊松比；∇为拉普拉斯算子。

（二）动力本构模型

本文采用Mohr-Coulomb模型模拟土体在地震往复作用下的动力响应。如图1所示，Mises屈服面在子午面和平面上呈对应关系。

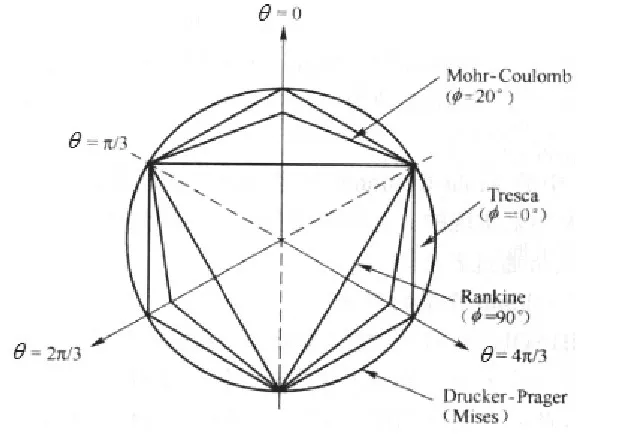
图1 Mohr-Coulomb模型中的屈服面

屈服面函数及塑性势面函数可分别表示为：

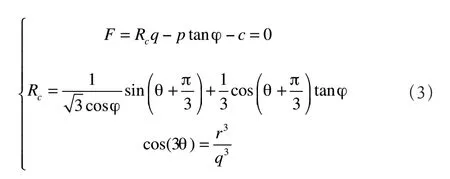
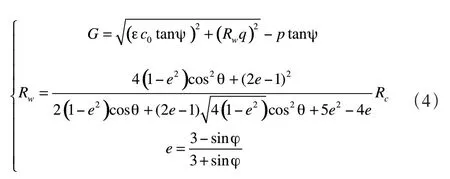
如公式（3）和公式（4）所示，q为等效剪应力；p为平均主应力；φ 为土的内摩擦角；c为土的黏聚力；r为第三偏应力不变量；ψ 为剪胀角；e为子午面上的偏心率。

（三）地震波输入类型及震动工况

如图2和图3所示，本文选用汶川波和EI Centro波作为该模型水平方向和垂直方向的输入波，地震波均以加速度时程方式输入。此外，根据抗震设计规范规定，该模型以峰值加速度为0.1g、0.2g和0.4g加载双向地震波，竖向地震动峰值取为水平向地震动峰值的2/3。地震波按照峰值加速度的大小由小到大施加，同时在加载完成后，及时完成所提取地震波的后处理，以方便过滤掉无用的噪音及反射波。

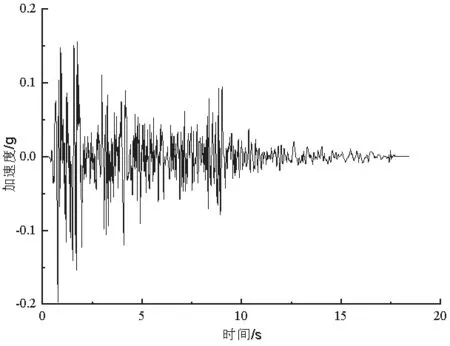
图2 EI地震波时程曲线

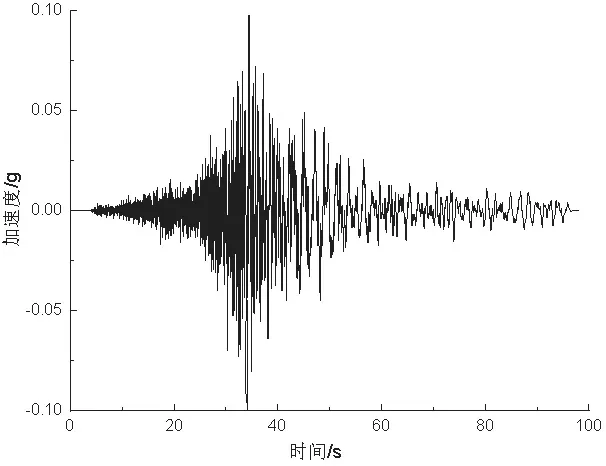
图3 汶川地震波时程曲线

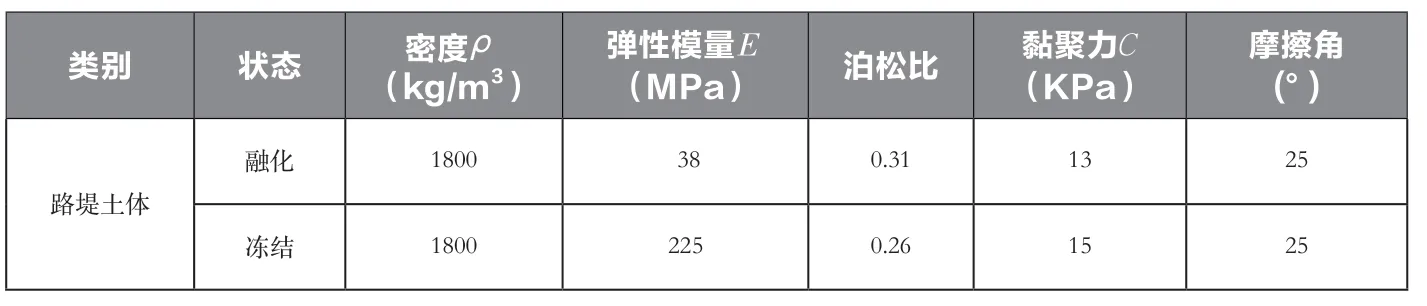
表1 有限元模型计算参数

（四）模型建立及边界条件施加

为符合实际工程中的路基形式，该模型根据已经竣工使用的青藏高速公路格拉段路基断面形式建立几何模型。路面材料为沥青混合料，路基高度为4.8m，坡度比为1∶1.5，路基顶部的坡度为2%。行车道宽度设置为3.7m，中心分隔为2m，路缘宽度为0.75m，几何模型及有限元网格图如图4和图5所示，有关模型参数如表1所示。

当分析高烈度地震作用下多年冻土区既有路基动力响应特性数值时，为防止地震波在该模型边界处反射，通常在有限模型尺寸近场计算区边界处引入虚拟的人工边界，以达到模拟半无限地基远场对散射波的吸收、消除反射波的目的。目前，在广泛应用的有限元软件中可以实现的主要有透射边界、黏性边界和黏弹性边界等人工边界，本文选用黏弹性人工边界，人工边界节点单位影响面积时的弹簧刚度和阻尼系数取值如表2所示。

结合一维波动理论，则任意高度位置任意时刻，三个方向的边界条件满足以下方程：

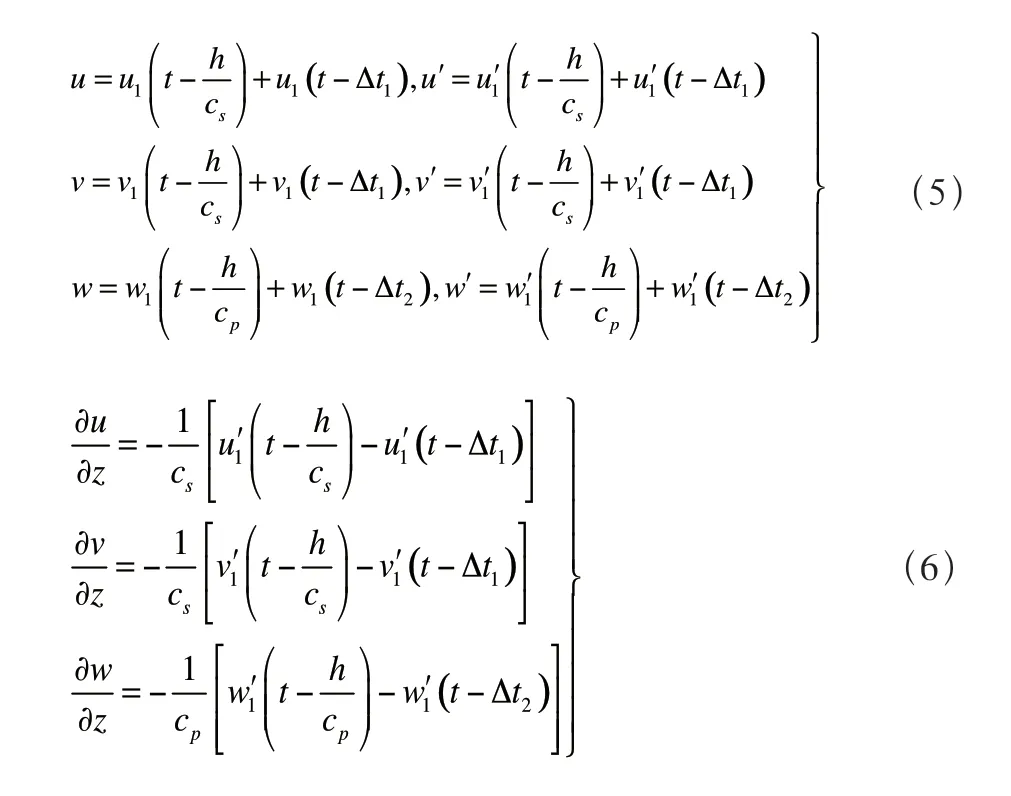
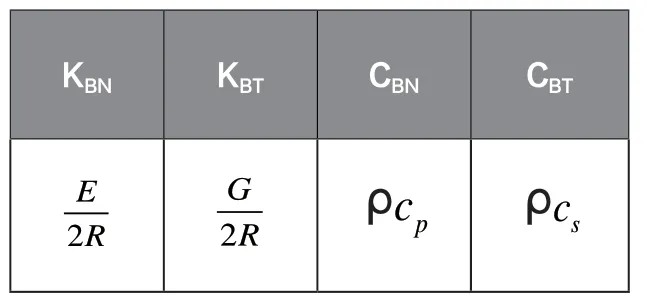
表2 刚度系数和阻尼系数计算公式

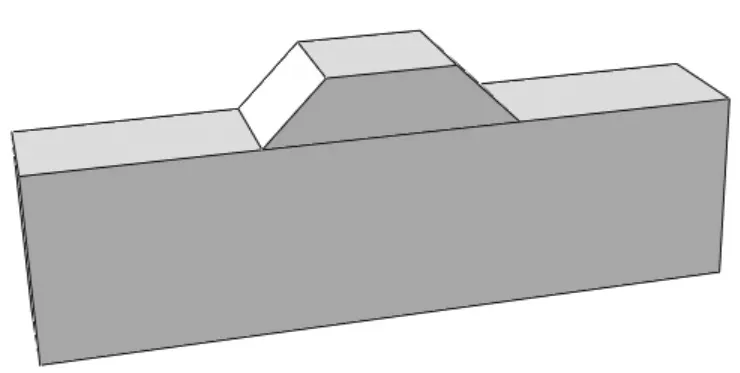
图4 路堤几何模型图

图5 有限元网格图

三、路基动力响应分析

为更好地评价高烈度地震作用下多年冻土区既有路基动力响应特性，本文提取分析了该模型典型的路堤坡底、坡面、坡肩及坡面顶部（路面）位置处在最大加速度峰值0.4g作用下的动加速度时程、动位移时程，典型监测点如图6所示。此外，由于路基结构形式是对称的，因此分析一半的路堤边坡，就可以获得同样的效果，这样不仅解决了计算过程繁琐的问题，而且还节约了时间及计算资源。

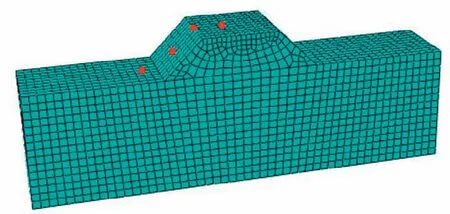
图6 典型监测点位置图

（一）动加速度响应

依据在峰值加速度为0.4g激振条件下的EI地震波和汶川地震波的典型位置处的加速度动力响应时程曲线可知，在EI地震波激振下，从路堤坡底至坡面的加速峰值范围为4.89m/s2～7.21m/s2，坡面加速度峰值比坡底大12.3%～22.1%；在汶川地震波激振下，从路堤坡底至坡面的加速峰值范围为4.01m/s2～7.28m/s2，坡面加速度峰值比坡底大15.7%～21.3%，表明地震波加速度峰值随着路堤高度增加而增加，具有明显的高程放大效应；不同位置处的加速度时程曲线与输入的地震波时程曲线变化趋势相似，峰值出现的时间基本一致；由于不同地震波激振下其加速度峰值不同，所以路堤对不同频谱特性地震波的响应是不同的，因此在今后路基抗震设计及验算时，应输入不同频谱特性的地震波进行核实，并在路肩位置处加强处理，以免该位置在地震发生时毁坏。

（二）动位移响应

依据在峰值加速度为0.4g激振条件下的EI地震波和汶川地震波的典型位置处的位移动力响应时程曲线可知，在EI地震波激振下，从路堤坡底至坡面的位移峰值范围为3.88mm～4mm；在汶川地震波激振下，从路堤坡底至坡面的位移峰值范围为11.2mm～13.1mm，表明不同地震波作用下位移响应是不同的，汶川地震波作用下该路堤的位移动力响应最大，破坏性最强烈，故在今后路基抗震设计及验算时，应输入不同频谱特性的地震波核实验证，以最不利的位移响应作为基准完成设计。

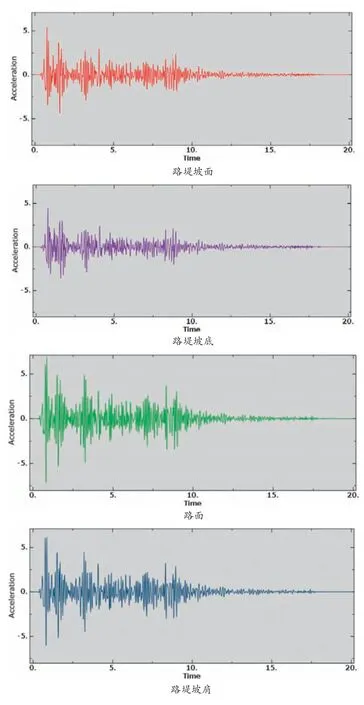
图7 EI波作用下路堤不同位置处的加速度动力响应

四、结语

在不同地震波作用下，多年冻土区路基不同位置处的加速度具有高程放大效应，在路堤坡顶位置处加速度响应峰值最大，在路堤坡地位置处加速度响应峰值最小。此外，不同位置处的加速度时程曲线趋势大体相似，但不同地震波激震下的放大效应是不同的。

同一地震波激振下，位移相应时程曲线趋势大体相似，位移峰值出现的时间相同，但是位移峰值略有不同。EI地震波激震下的位移明显比汶川地震波激振时的位移小，表明汶川地震波对该多年冻土区路堤破坏性较大，同时也表明不同频谱特性的地震波激振时，其位移响应也是不同的。