胶合木植筋节点抗拔性能理论预测

凌志彬,陆 帆,杨会峰

(1.苏州科技大学 土木工程学院,江苏 苏州 215011;2.南京工业大学 土木工程学院,江苏 南京 211800)

植筋技术早期主要用于混凝土结构的扩建、改造与加固,许多学者对混凝土后锚固植筋进行了大量研究[1-5]。随着现代木结构的快速发展,植筋技术也被引入到木结构工程领域,用于木梁、木柱等构件之间的连接,即木结构植筋节点[6]。近年来,许多国内外学者对木结构植筋节点进行了研究[7-13],结果表明:相比于榫卯[14]、钉节点[15]等传统木结构节点,木结构植筋节点具有相对较高的承载力和初始刚度,且经合理设计的节点能实现延性破坏。目前,植筋技术在国内外木结构中已经得到了一些应用。图1为国内外采用植筋连接的木结构工程典型案例。图1(a)为2000年悉尼奥运会会展中心(木网壳穹顶,穹顶直径达98 m),该网壳的节点连接部位采用了木结构植筋连接。图1(b)为江苏省第九届园艺博览会木结构主展馆,其主体结构为自由曲面木网壳,局部构件之间采用木结构植筋连接。图1(c)为不列颠哥伦比亚大学学生公寓,正交胶合木楼板与木柱交接处采用螺栓杆植筋与钢套管混合连接,将上下层木柱拼接在一起。图1(d)为位于西班牙的某木结构空间网架,该结构所有杆件为中空胶合木杆,杆件与网架节点之间通过杆件端部的木结构植筋节点连接成整体[16]。

图1 采用木结构植筋节点的典型案例Fig.1 Typical applications of glue laminated timber joints with glued-in rod

虽然,木结构植筋已得到了成功应用,但其应用并不广泛,主要受制于目前关于木结构植筋节点抗拔承载力的理论计算公式尚不成熟,国际上还没有形成统一的规范条文。另外,目前关于木结构植筋节点抗拔过程的理论分析大多基于线弹性理论进行,只适用于短锚固木结构植筋节点的极限抗拔承载力预测,而对于长锚固木结构植筋节点则不太适用。鉴于此,本文基于笔者提出的胶合木植筋节点黏结应力-滑移关系[8],根据能量守恒法则,推导并建立了胶合木植筋节点抗拔承载力-滑移关系,进而对胶合木植筋节点的抗拔全过程进行预测。本文的研究将为今后形成统一的木结构植筋节点规范条文提供一定的理论依据,同时也有助于促进植筋节点在木结构领域得到更广泛的应用。

1 试验

1.1 材料

本次试验所用胶合木由北美花旗松层板制作而成,其力学性能如表1所示。

表1 胶合木力学性能

植筋杆件为HRB335级螺纹钢和M8.8级高强螺栓杆,直径为16 mm。通过拉伸试验测得螺纹钢和螺栓杆的抗拉屈服强度标准值分别为362和695 MPa,弹性模量为200 GPa。

胶层采用双组分环氧树脂胶黏剂,抗拉强度和抗压强度分别为92.7和84.3 MPa,钢与钢界面黏结强度为22.0 MPa,弹性模量≥1.5 GPa。需要说明的是,上述胶黏剂的力学性能由供应商(南京曼卡特公司)提供。

1.2 试件设计

设计并制作了6组胶合木植筋试件,每组各5个。为避免木材发生过早劈裂,植筋边距设计为植筋直径的5倍。另外,为了避免锚固端和试验端应力场的相互影响,取lm=1.4la,lm和la分别为试验端与锚固端间孔底净距和试验端植筋锚固长度;而对于部分长锚固试件,考虑到试验机空间有限,取lm=1.2la。所有试件的胶层厚度(t)设计为2 mm。表2给出了胶合木植筋试件的尺寸,图2为试件示意图。

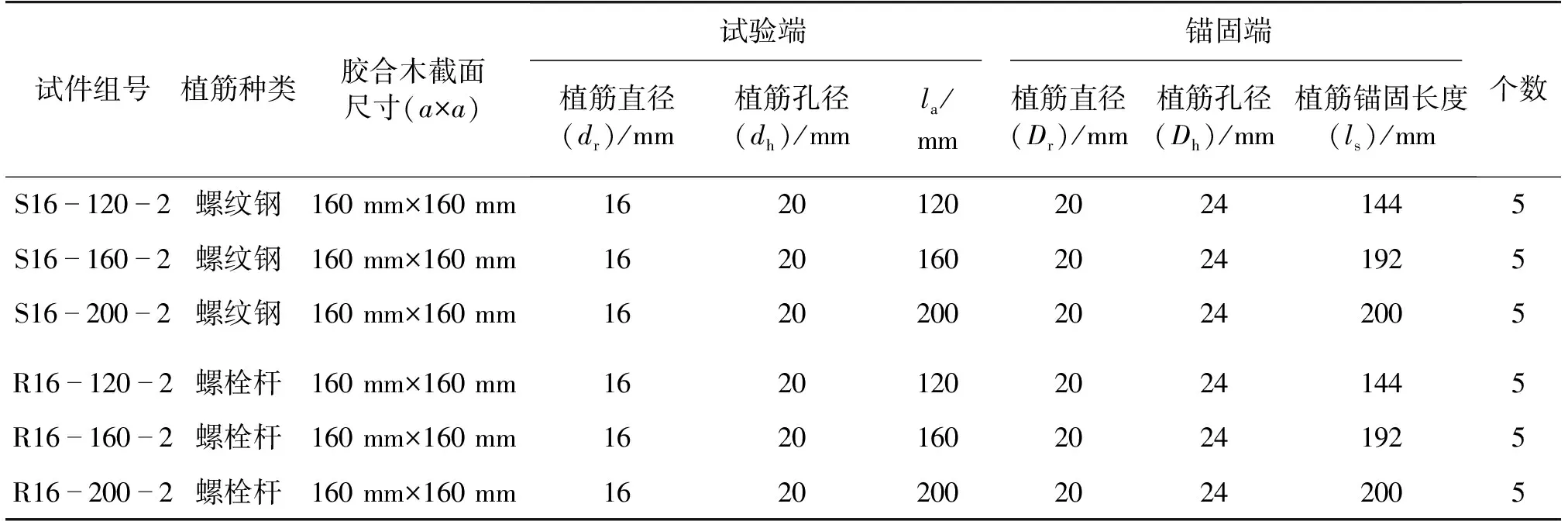
表2 胶合木植筋试件列表

图2 试件示意图Fig.2 Schematic of specimens

1.3 试验装置与加载制度

本次试验在量程为1 MN的电液伺服万能试验机上进行。采用位移控制模式,以2.0 mm/min的恒定速率进行加载,直至试件破坏。加载装置如图3所示。需要说明的是,木材与钢筋之间的相对滑移可通过位移计及自主设计的位移辅助装置测得。位移辅助装置通过管卡固定在试验端的植筋上,且距离木材端部约5 mm,位移计对称固定在胶合木两侧,固定点与位移辅助装置间距离设计为20 mm。

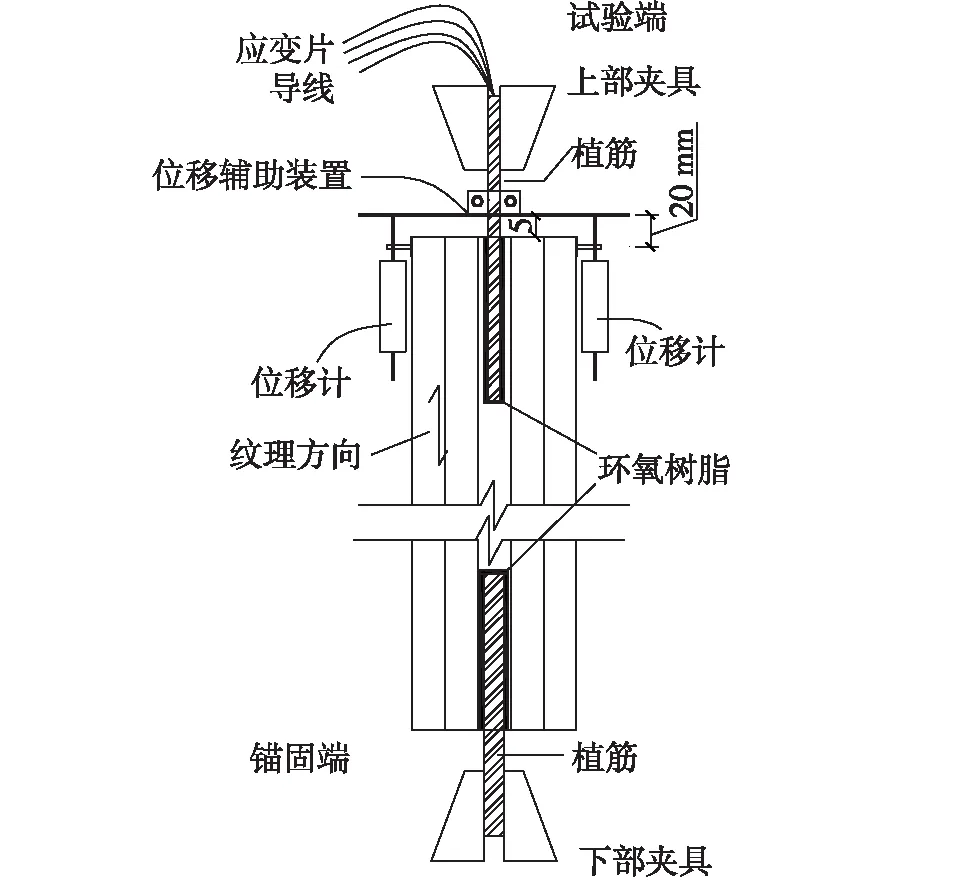
图3 试验装置及测点布置Fig.3 Test setup and measuring point layout

2 试验结果与分析

2.1 典型的破坏模式

图4(a)—4(c)为螺纹钢植筋试件的破坏模式。由图4(a)—4(c)可知:植筋拔出破坏主要是由于植筋的锚固长度相对较短,胶层与植筋界面提供的抗拔承载力有限,因此当外荷载达到一定级别时,发生植筋/胶层破坏，即拔出破坏。S16-160-2组试件的锚固长度为160 mm,该组试件最终的破坏模式为木材环向剪切破坏。对于长锚固试件(S16-200-2),当锚固长度达到一定值,植筋与胶层、木材之间的黏结界面提供的黏结力大于植筋的屈服承载力,因此植筋会发生明显的颈缩行为。图4(d)和4(e)为螺栓杆植筋试件的破坏模式。由图4(d)和4(e)可知:所有螺栓杆植筋试件的破坏模式均为植筋周围木材环向剪切破坏，主要是由于螺栓杆表面的细螺牙与胶层之间形成了很好的黏结力和咬合力,在整个加载过程中,螺栓杆/胶层界面没有发生任何破坏,而木材的顺纹抗剪强度是有限的,因此荷载达到一定值时,就会发生螺栓杆周围木材剪切破坏。

图4 典型的破坏模式Fig.4 Typical failure modes

2.2 荷载-滑移曲线

图5为各组试件的荷载-滑移试验曲线以及理论计算曲线。由图5可知:不同种类植筋试件的荷载-滑移曲线存在一定差别。对于短锚固螺纹钢植筋试件(S16-120-2),加载初期，荷载与滑移呈线性增长关系,随后进入非线性增长至峰值荷载,此时试件已发生明显的拔出破坏,峰值过后荷载-滑移曲线逐渐软化下降,此过程中主要是植筋表面肋与胶层之间的摩擦提供残余承载力。对于中长锚固螺纹钢植筋试件(S16-160-2及S16-200-2),加载初期,荷载-滑移曲线基本呈线弹性上升趋势,对于锚固长度为160 mm的试件,曲线随后出现了软化下降行为;对于锚固长度为200 mm的试件，曲线表现出明显的屈服平台,说明此时的植筋已发生屈服,即当锚固长度达到一定值时,胶合木植筋节点能实现延性破坏。对于螺栓杆植筋试件,在整个加载过程中,荷载基本上与滑移保持线性增长关系至峰值点,随后曲线发生急剧下降，这是因为试件发生木材环向剪切破坏,属于脆性破坏模式。

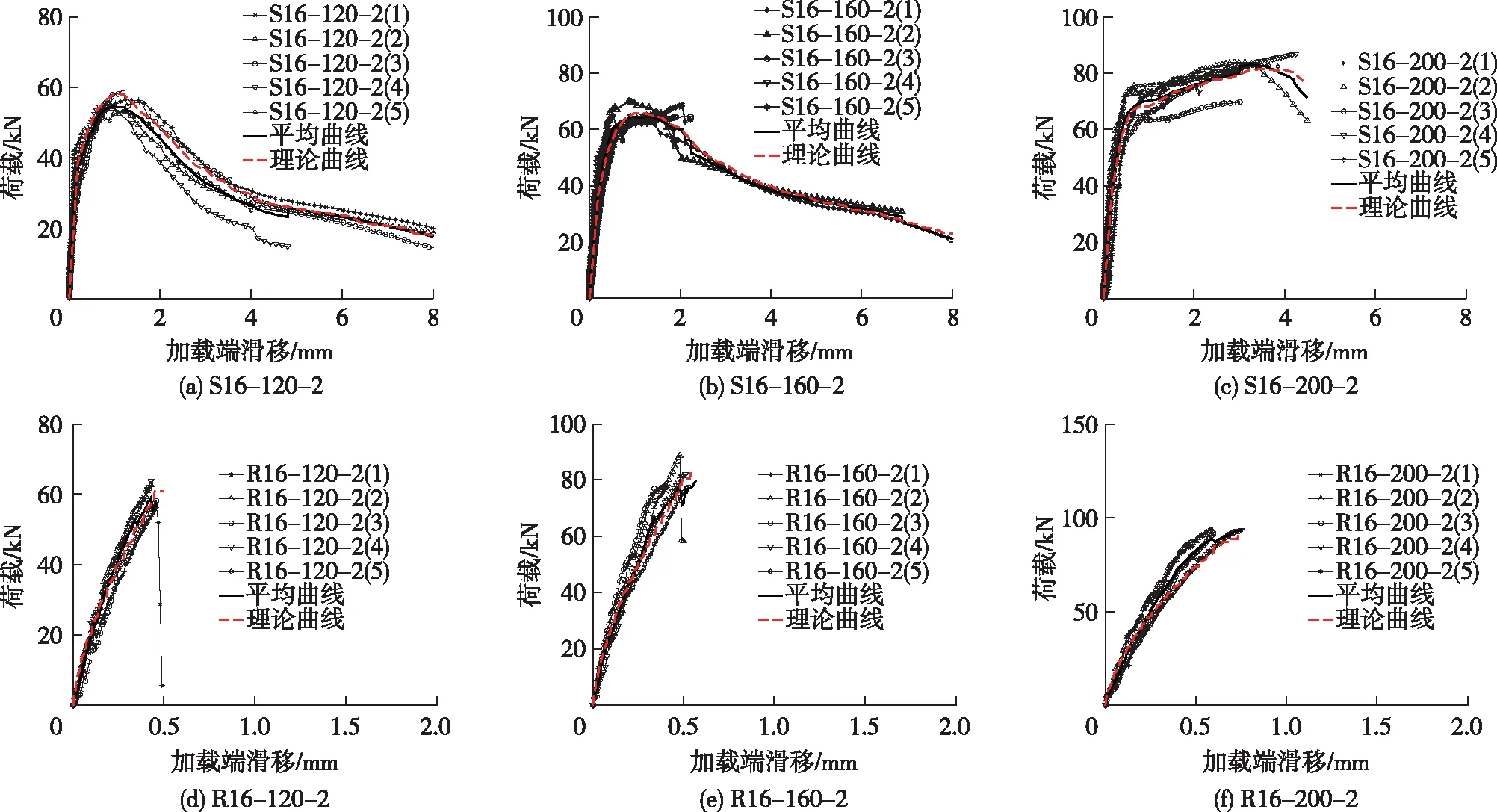
图5 荷载-滑移关系理论与试验曲线对比Fig.5 Comparison of theoretical and experimental load-slip curves

3 胶合木植筋节点抗拔性能预测

3.1 黏结应力-滑移模型

目前,国内外学者已建立了多个黏结应力-滑移模型,涉及钢筋与混凝土、纤维增强复合材料(FRP)与混凝土之间的黏结,如Eligehausen等[17]提出的Bertero-Eligehausen-Popov(BEP)模型,Cosenza等[18]提出的改进后的BEP模型,高丹盈等[19]提出的连续曲线模型等。但这些模型仍存在一些问题:①曲线的黏结应力峰值处不够连续光滑;②模型中参数较多,且部分为半经验参数;③部分参数没有明确的物理意义,有一定的局限性。

笔者基于试验,在总结现有的黏结应力-滑移关系基础上,提出了适用于胶合木植筋的黏结应力-滑移模型[8],如图6所示，图中τ为胶层黏结应力,等于荷载-滑移曲线上的荷载与植筋黏结面积的比值;s为与τ对应的滑移;τm为峰值黏结应力,等于荷载-滑移曲线上的峰值荷载与植筋黏结面积的比值;sm为与τm对应的滑移;τu为残余黏结应力;su为τu对应的位移。

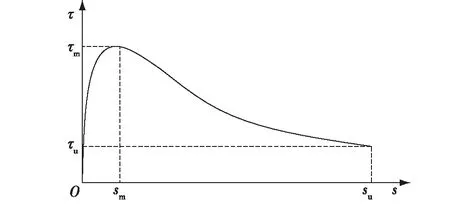
图6 胶合木植筋黏结应力-滑移模型Fig.6 Bond stress-slip model of glue laminated timber with glued-in rod

上升段计算式为

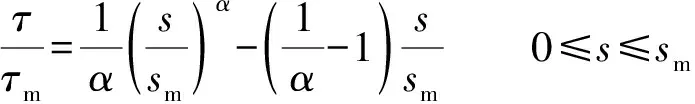
(1)

下降段计算式为

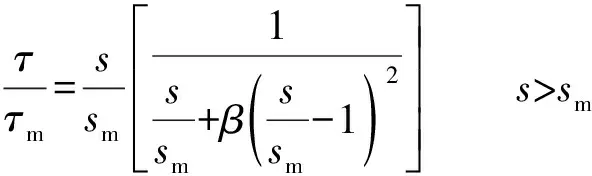
(2)

式中:α、β分别为表征初始黏结刚度和黏结“软化”行为的参数,取值详见表3。

与其他黏结应力-滑移模型相比,该模型具有如下特点:在s=0处,τ=0和dτ/ds=∞;在s=sm处,τ=τm。

由此可见,提出的黏结应力-滑移模型满足在黏结应力峰值处连续光滑的条件。

由于本文涉及的部分试件发生了植筋屈服破坏,且最终破坏发生在植筋强化阶段。因此,本文仅采用Ashtiani等[20]提出的可考虑屈服效应的黏结应力-滑移关系中的屈服段和强化段来描述本文的植筋屈服后的黏结应力-滑移行为,分别如式(3)和(4)所示。

τ=τy

(3)

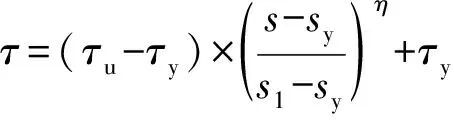
(4)

式中:τy、sy分别为曲线屈服点处的黏结应力及滑移,s1为最大黏结应力对应的滑移,η为表征强化段滑移的特征参数(表3)。

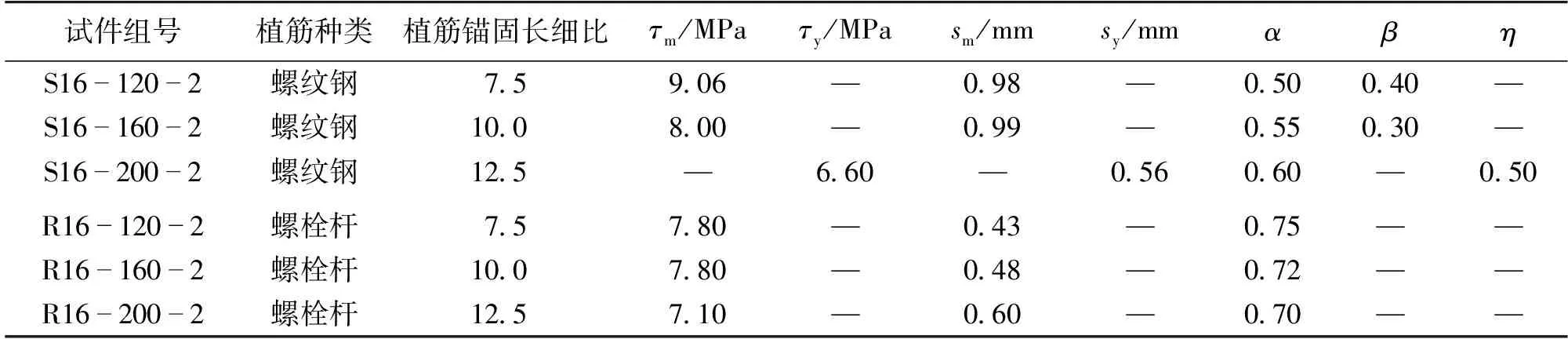
表3 胶合木植筋节点黏结应力-滑移模型参数

3.2 基于线弹性理论的抗拔承载力预测

后锚固植筋最早用于混凝土结构的加固与补强。通常在锚固设计时假设植筋与混凝土之间界面的黏结应力沿锚固方向均匀分布,以便于设计计算,即锚固界面的面积与黏结应力的乘积等于植筋的锚固承载力。然而,黏结应力沿锚固方向均匀分布这一假定可能适用于短锚固植筋试件,但对于长锚固植筋试件,由于界面黏结应力分布存在明显的不均匀性,基于该假定计算得到的结果将偏于不安全。

Cook[21]首先分析了混凝土植筋发生的胶层界面破坏,基于混凝土与胶黏剂界面的黏结应力和接触面的位移协调条件,建立了弹性分析模型；然后通过弹性理论对混凝土植筋锚固体系的极限承载力进行计算,并用能量法建立了体系的位移微分方程；最后借助最小势能原理,计算得到了植筋的极限承载力。

木结构植筋系统与混凝土后锚固植筋类似,植筋体系的内部能量主要为植筋和胶黏剂的应变能,植筋体系弹性分析模型如图7所示，图中k为胶层剪切刚度,P为外荷载,w为植筋轴向变形,z为沿植筋轴向坐标。

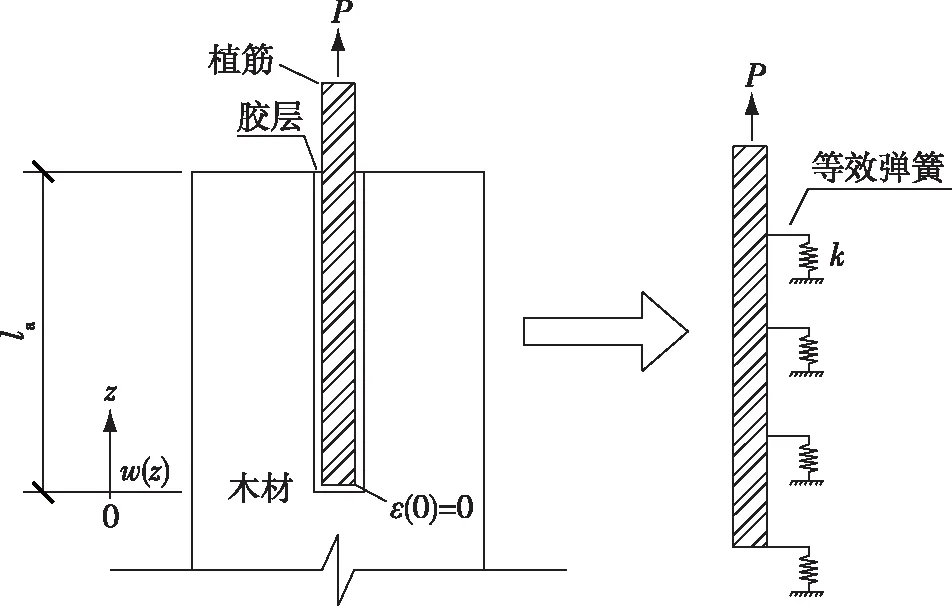
图7 木结构植筋线弹性模型Fig.7 Linear elastic model for glued-in rod in timber

植筋的应变能(ΠGIR)为

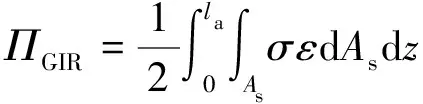
(5)

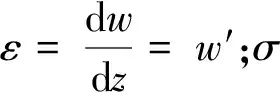
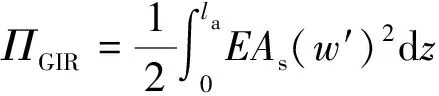
(6)

胶黏剂的应变能(Πadv)为

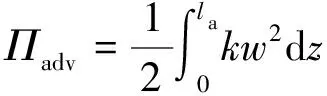
(7)

植筋拔出力所做的功(Πext)即为植筋抗拔过程中植筋伸长所做的功。

Πext=-Pw(z)

(8)

系统的总能量(Πt)为

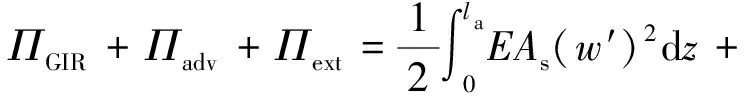
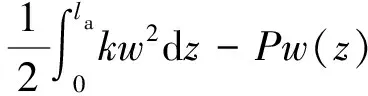
(9)

对上式求极小值，如式(10)所示。

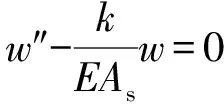
(10)

胶层的剪切刚度(图8)可表示为

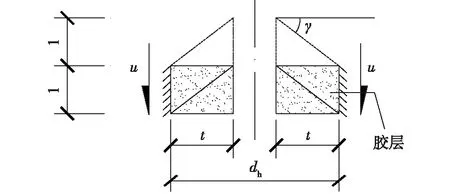
图8 胶层剪切刚度Fig.8 Shear stiffness of bond-line

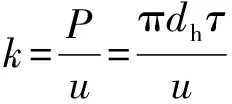
(11)

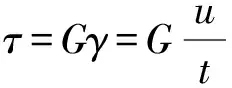
(12)

式中:τ、G、γ分别为胶层剪切应力(即黏结应力)、剪切模量、剪应变,u为单位长度胶层在P作用下的剪切变形。

将式(12)代入式(11)，得胶层剪切刚度为

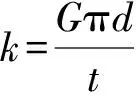
(13)

将式(13)代入式(10),得微分方程为

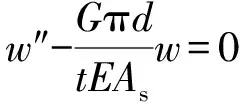
(14)

转化为

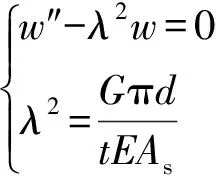
(15)

通解为

w(z)=Asinh(λz)+Bcosh(λz)

(16)

w′(z)=λ(Acosh(λz)-Bsinh(λz))

(17)

式中:A、B为自定义参数。

边界条件为

ε(0)=w′(0)=0

(18)

ε(la)=w′(la)=P/EAs

(19)

将边界条件代入式(17)可解A和B的值,求得

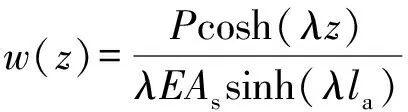
(20)

γ(la)=τmax/G，τmax为加载端处的最大界面黏结应力，且γ(la)=w(la)/t,则

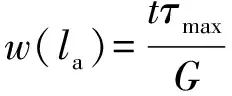
(21)

将式(21)代入式(20)，求得植筋锚固体系的极限抗拔承载力(Pu)，如式(22)所示。

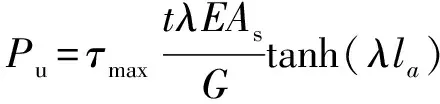
(22)

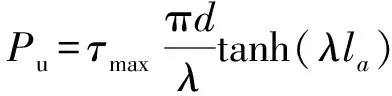
(23)

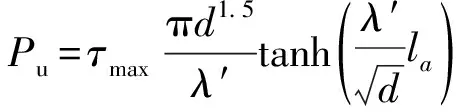
(24)

Pu即为由线弹性分析理论求得的植筋极限抗拔承载力,式中的τmax、λ′的值均可由试验获得。

表4为极限抗拔承载力试验值与线弹性理论推导结果对比。由表4可见:式(24)计算得到的木结构植筋节点的极限抗拔承载力总体上明显低于试验值,尤其是在植筋锚固长度相对较大的情况下,说明基于线弹性理论推导的植筋节点极限抗拔承载力计算公式过于保守地估计了实际极限抗拔承载力。

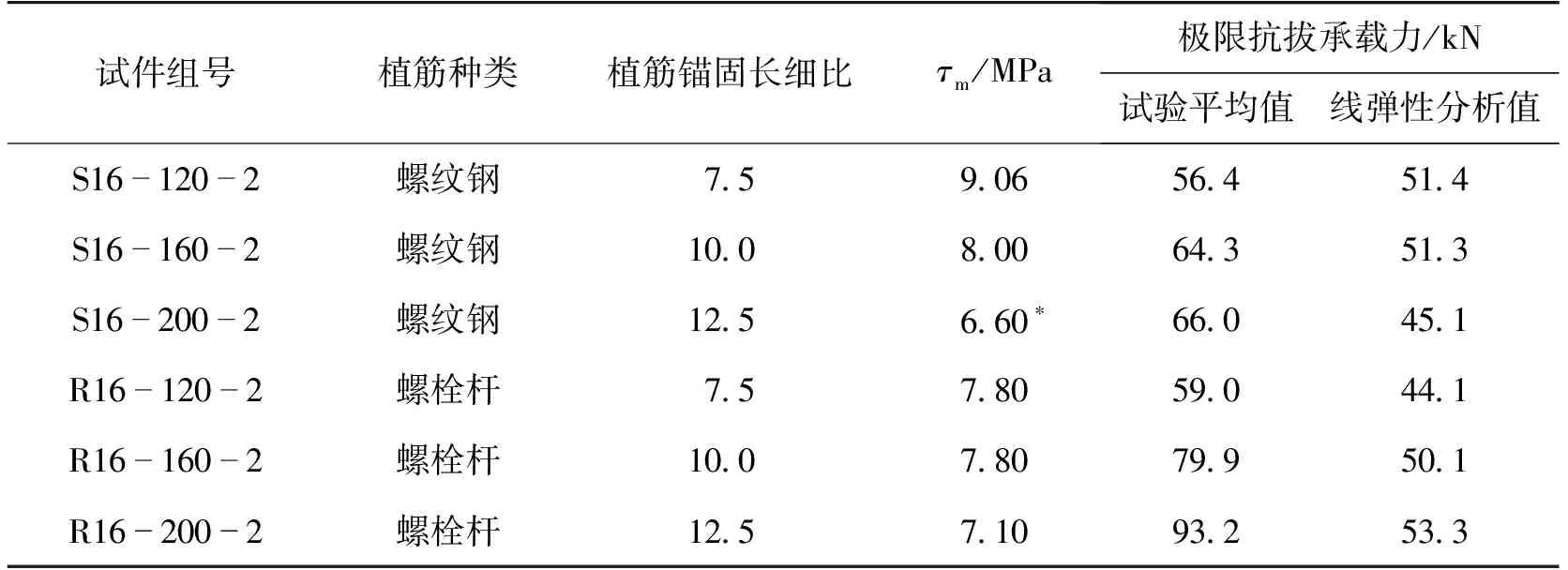
表4 极限抗拔承载力试验值与线弹性理论推导结果对比

3.3 非线弹性抗拔全过程分析

根据上节线弹性理论分析中的假定条件,相当于假定了黏结应力-滑移关系为线性比例关系。对于短锚固植筋试件,能够较好地预测植筋的极限抗拔承载力,但对于长锚固植筋试件,假定条件将不再成立,所得计算结果过于保守。根据提出的黏结应力-滑移关系,本节将对胶合木植筋节点的抗拔过程进行全过程理论预测,并将理论计算与试验曲线进行对比。

图9为胶合木植筋黏结界面处各参数沿锚固长度的分布模型。基于提出的黏结应力-滑移关系,外力引起的界面黏结应力所做的功(Wext)为

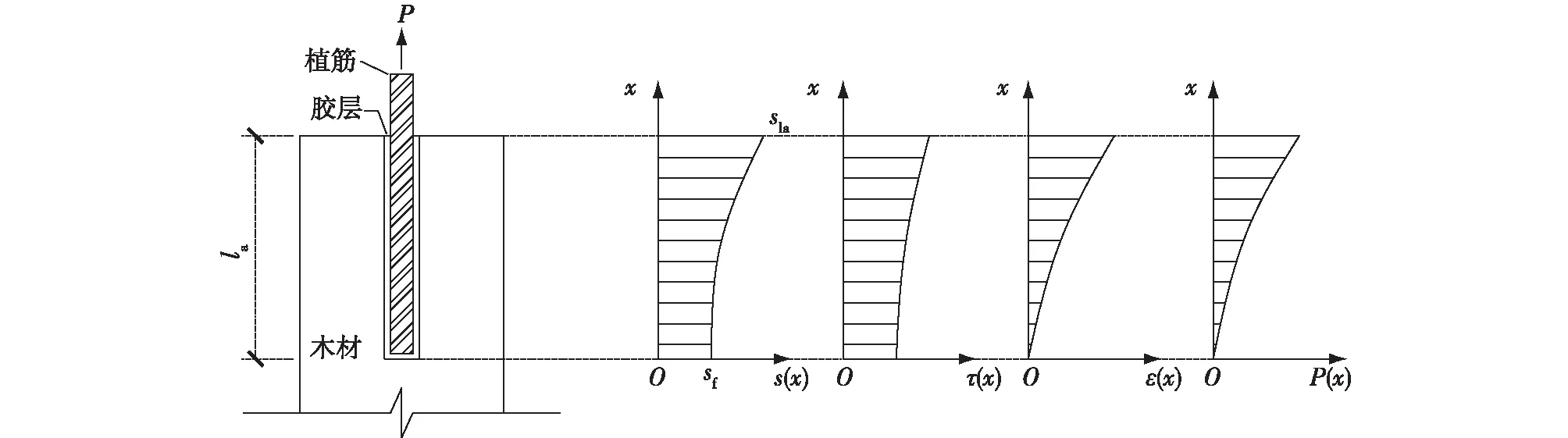
图9 界面参数沿锚固长度分布模型Fig.9 Distribution model of interfacial parameters along anchorage length

τm取植筋屈服荷载对应的黏结应力进行分析。

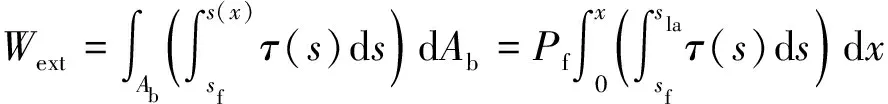
(25)

式中:x为沿植筋深度方向的位置,s(x)为黏结界面x处植筋与胶合木之间的相对滑移,τ(s)为界面黏结应力,Ab、Pf分别为黏结界面的面积与周长,sf、sla分别为植筋自由端和加载端的滑移。

传统拔出试验中,黏结界面不同位置处的相对滑移一般通过从自由端开始对植筋应变进行积分求得;而对于两端对拉试验,由于只能测得试件加载端的相对滑移,因此考虑从加载端进行递减推算,求出胶合木植筋黏结界面不同位置处的相对滑移,传统拔出试验和两端对拉试验计算式分别如式(26)和(27)所示。

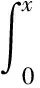
(26)

(27)

根据轴力平衡关系得

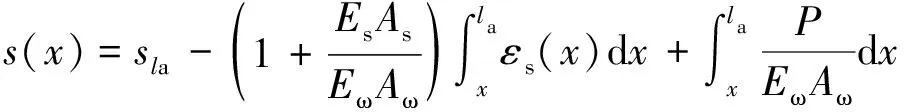
(28)

式中:εs、εω分别为植筋和木材截面的应变，Es、Eω分别为植筋与木材的弹性模量，Aω为木材的截面面积。

关于式(28)的推导过程及具体的计算结果,详见文献[8]。

界面黏结处植筋的应力应变能(Wint)为

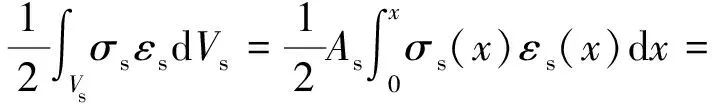
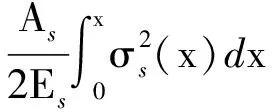
(29)

式中:σs为植筋的轴向应力，Vs为植筋的体积。

基于能量守恒法则,植筋的应力应变能与外力引起的界面应力所做的功相等,如式(30)和(31)所示。

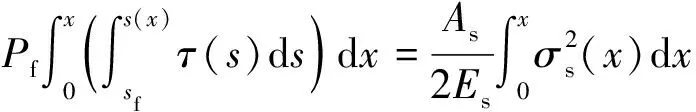
(30)

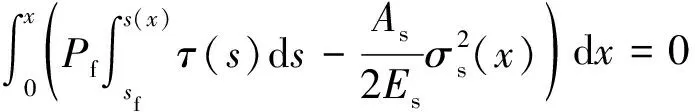
(31)

显然,式(29)对任意x成立的条件为

(32)

在加载端x=la处,式(32)可表示为

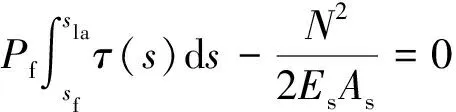
(33)

在不同滑移下,加载端处的植筋轴力(N)可表示为

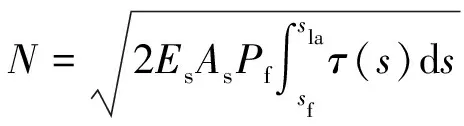
(34)

根据式(34)可计算得到试件加载端处植筋轴力与滑移之间的关系曲线,图5给出了荷载-滑移关系试验曲线与计算曲线的对比。由图5可知：基于黏结应力-滑移关系计算得到的荷载-滑移关系理论与试验曲线吻合较好,能有效地反映植筋抗拔的全过程行为,与基于线弹性理论分析得到的计算结果相比,结果更准确。

4 结论

本文基于试验和理论推导对胶合木植筋节点的抗拔性能进行了研究。

1)螺纹钢植筋试件主要发生植筋拔出破坏、植筋周围木材剪切破坏和植筋屈服破坏;螺栓杆植筋试件的破坏主要表现为植筋周围木材剪切破坏。

2)螺纹钢植筋与螺栓杆植筋试件的荷载-滑移行为存在一定差别，且螺纹钢植筋试件的荷载-滑移行为与锚固长度有关。

3)根据传统的线弹性理论,推导得到的胶合木植筋节点的极限抗拔承载力计算公式过于保守地估计了节点的实际极限抗拔承载力。

4)基于能量法,借助已提出的黏结应力-滑移关系模型进行理论推导,所建立的试验端植筋抗拔承载力-滑移的理论计算模型能够实现植筋抗拔全过程预测,且理论计算与试验曲线吻合良好。