全感知条件下基于奖励塑形的Q-learning算法及仿真

陈嘉楠,彭军海,黄 华

(1.中国人民解放军91404部队,河北 秦皇岛 066000；2.江苏自动化研究所,江苏 连云港 222061)

强化学习(Reinforcement Learning)一词最早被Minsky[1]提出。不同于监督学习和非监督学习,强化学习模仿人类学习模式，即通过让智能体与环境交互,用环境反馈的奖励指导策略函数的改进。Q-learning算法最早是由Watkins在1989年提出[2],是最经典的价值学习(Value-Based Learning)方法之一,其以Q表格近似最优动作价值函数Q*(s,a),做决策时使用Q表格指导智能体选择动作。Q-learning算法在解决状态-动作空间维数较小的强化学习问题时获得了不错的表现,但是在解决状态-动作空间维数较大的稀疏奖励问题时效果常常不尽如人意。

Sutton[3]指出,强化学习的目标可以归结为:最大化智能体接收到的累积奖励的概率期望值。在强化学习过程中，奖励被认为是“上帝”在给智能体的动作打分。然而在实际项目中大部分状态下奖励信号都为0,即所谓稀疏奖励问题(Sparse Reward Problem)。面对稀疏奖励问题,通常我们都会根据先验经验及对环境的认知,人为设计一些奖励函数来辅助学习算法。这种将先验知识转化为附加奖励函数,从而引导学习算法学得更快、更好的方式,叫作奖励塑形(Reward Shaping)。大量学者对奖励塑形进行了研究。吴恩达[4]最早提出基于势能的奖励塑形(PBRS),并证明使用此奖励塑形后,智能体的最优策略不变。Wiewiora[5]将PBRS势函数定义在状态动作联合空间,并证明了PBRS等价于为值函数提供一个初始值。Sam[6]尝试采用动态可变的势函数构造塑形奖赏。Harutyunyan[7]通过学习的方法让势函数表达出任意给定的附加奖励函数,从而避免手工设置势函数的麻烦。Suay[8]提出RE-IRL,直接将逆强化学习学到的奖励函数转换为奖励塑形函数。随着深度强化学习的发展以及越来越复杂的实际问题的出现,近年来的一些奖赏塑形方面的工作更多地关注如何让学习算法学得更好。Ofir[9]提出基于信念的奖赏塑形方法；HaoshengZou[10]提出基于元学习的奖赏塑形方法；Zhao-Yang Fu[11]提出塑形奖赏函数自动选择框架；网易伏羲[12]提出了一种新型的奖励塑形方法,该方法能够自适应地对给定的塑形奖励进行选择性利用,从而避免过度利用先验知识使得强化学习算法效果反而变差的潜在风险。

本文提出全感知条件下基于奖励塑形的Q-learning算法。假定智能体对环境全局具备完全感知能力,通过设计带惩罚项的势函数构造奖励塑形函数,解决Q-learning算法在状态-动作空间维数较大的稀疏奖励问题时训练无法收敛问题;同时针对智能体在训练过程中选择明显不合适的动作导致训练提前中止问题,利用智能体对四周的感知能力,改进ε-greedy行为策略函数,避免智能体在训练过程中进行明显不合适的探索。仿真结果表明，全感知条件下基于奖励塑形的Q-learning算法能够稳定训练智能体,相比于基于奖励塑形的Q-learning算法,收敛速度更快,收敛效果更稳定。

1 算法基础

1.1 强化学习与马尔科夫决策过程

强化学习通过智能体不断与环境进行交互,并获得环境反馈的奖励R。智能体试图找到一个决策规则使得其折扣回报Ut=Rt+γRt+1+γ2Rt+2+…最大。强化学习中智能体与环境交互关系如图1所示。

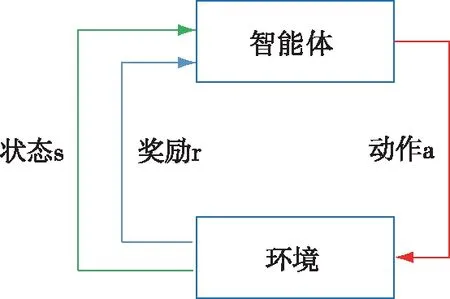
图1 智能体与环境交互关系

强化学习的数学基础是马尔科夫决策过程(MDP),一个MDP通常由一个五元组来表示:

M={S,A,P,R,γ}

(1)

其中，S为状态空间，A为动作空间，P:S×A×S′∈[0,1]为状态转移概率函数，R:S×A×S′→R为奖励函数,γ∈[0,1]为折扣因子。

1.2 Q-learning算法

假定状态空间S和动作空间A都是有限集,且dimS=n,dimA=m,那么最优动作价值函数Q*(s,a)为一个n×m的表格。由最优贝尔曼方程[3]:

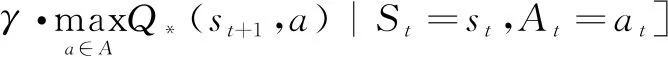
(2)

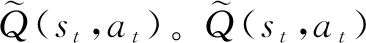
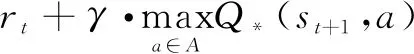
(3)

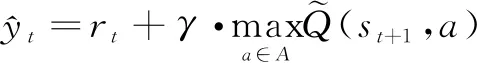
(4)

它是表格在t+1时刻对Q*(st,at)的估计。使用TD目标更新Q表格:

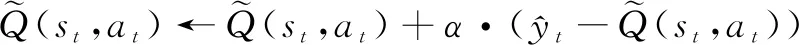
(5)

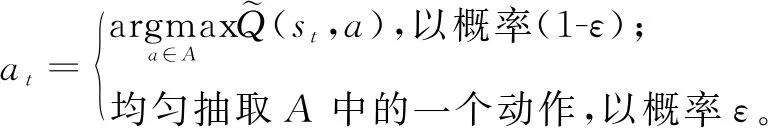
(6)

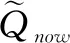
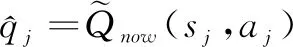
(7)

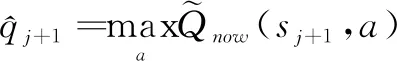
(8)

3)计算TD目标和TD误差:

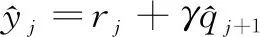
(9)

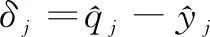
(10)

4)更新表格中(sj,aj)位置上的元素,同时对ε进行递减:

(11)

ε=ε-εdec

(12)

本文采用与环境交互一次后立即对Q表格进行更新的方法。Q-learning算法伪代码如下:

Q-learning算法 1: 初始化Q, ε, γ, α, εdec2: 得到智能体当前状态3: 当(仿真次数<最大仿真次数且为非中止状态)循环执行:4: 如果产生的随机数<ε:5: 在当前状态下选择一个随机动作6: 否则:7: 根据Q值,选择当前状态下价值最高的动作8: 执行选择的动作,得到奖励rj9: 更新Q10: 进入下一个状态11: sj←sj+112: ε-=εdec13: 结束

1.3 奖励塑形

给定一个马尔科夫决策过程M={S,A,P,R,γ},奖励塑形是指在原有的奖赏函数R上附加奖励函数F:S×A×S′→R,从而得到一个重塑后的奖励函数R′=R+F和修正的马尔可夫决策过程M′={S,A,P,R′,γ}。

修正后的马尔科夫决策过程M′只是奖赏函数与原马尔科夫决策过程M有所不同,其他组成部分均一致。显然,由于M和M′的奖赏函数不同,它们各自的最优策略很可能也不相同。如果原有问题的最优策略发生了改变,那么添加塑形奖赏就失去了意义。因此,有很多工作关注于如何保持策略不变性(policy invariance),即如何使得M′的最优策略也是原有问题M的最优策略。吴恩达提出基于势能的奖励塑形方法(Potential-based Reward Shaping,PBRS)能够确保策略不变,其奖励塑形函数形式为

F(s,a,s′)=γφ(s′)-φ(s)

(13)

其中，φ:S→R为势能函数。策略不变性证明过程可以参考文献[4]。

如何运用先验经验,巧妙设计奖励塑形函数,是奖励塑形的关键。

2 全感知条件下基于奖励塑形的Q-learning算法设计

2.1 仿真环境介绍及分析

OpenAI Gym是一款用于研发和比较各类强化学习算法的工具包,提供了多种多样的环境,并且所有的代码均开源,开发者可以轻松地使用其环境，验证自己提出的算法的有效性。本文用OpenAI Gym生成试验所需的Fronzen Lake迷宫环境。默认情况下,环境会生成一个如图2的4*4的迷宫。

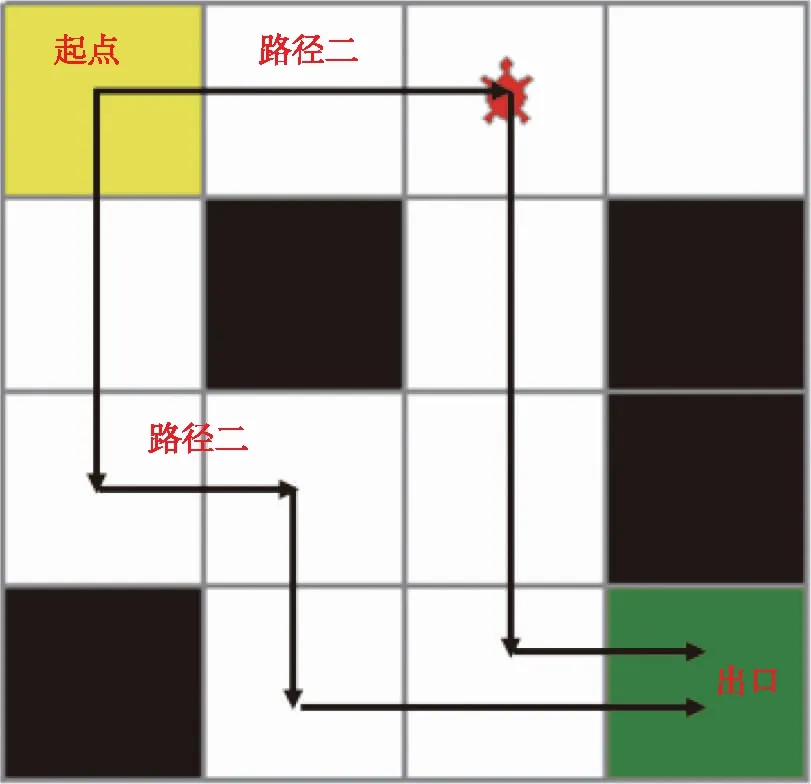
图2 4*4迷宫

图2中黄色位置代表迷宫起点(ss),绿色位置为迷宫出口(sg),黑色位置为悬崖(sh),红色智能体(agent)可以上下左右移动,一次仿真(episode)步数最多为500步,掉落悬崖、走出迷宫或仿真循环等于500步则一次仿真结束。成功到达迷宫出口位置获得+1奖励,其他情况下奖励为0,显然该奖励为稀疏奖励。奖励函数可以描述为

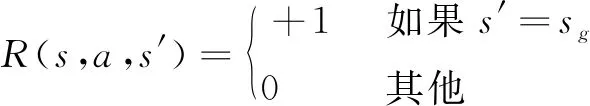
(14)

4*4迷宫环境状态空间为:S={0,1,…,15},动作空间为:A={0,1,2,3}(其中，0代表动作左,1代表动作下,2代表动作右,3代表动作上)。图2所示的路径一和路径二均是最优解,最优解的仿真步数为6步。使用1.2节Q-learning算法进行仿真。仿真过程中设置超参γ=0.9,ε=0.1,α=0.1,εdec=0.0001。仿真步数与累积奖励如图3所示。

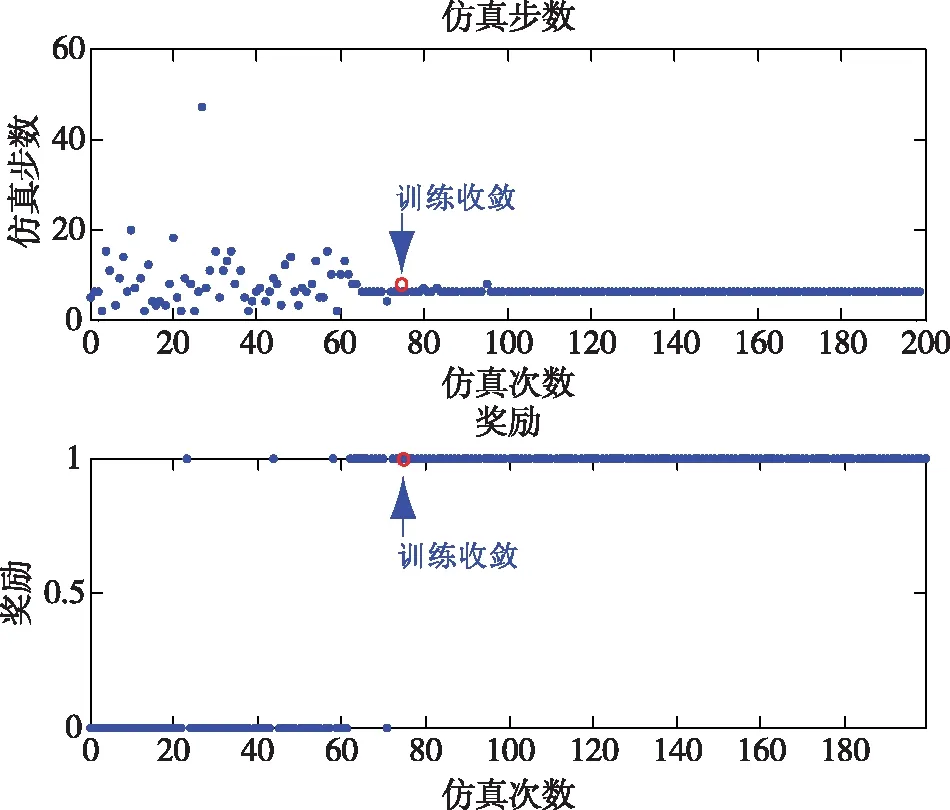
图3 4*4迷宫环境下仿真步数与累积奖励图

仿真表明,智能体在第73次仿真时奖励为1,仿真步数为6,找到最优解训练收敛。在状态-动作空间维数较小的时候,Q-learning也能在稀疏奖励下较快达到训练目标。

将状态空间扩大,构建15*15的如图4所示的迷宫。

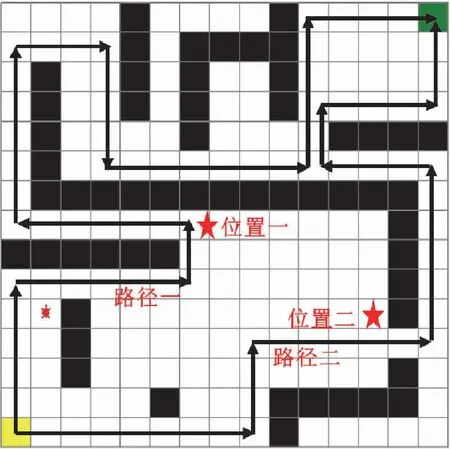
图4 15*15迷宫

环境状态空间和动作空间为:S={0,1,…,224},A={0,1,2,3}。构建的15*15迷宫起点位于迷宫左下角,出口位于迷宫右上角,智能体需要通过路径一或者路径二才能找到出口。

综合分析,通过路径一到达迷宫出口仿真步数为48步,通过路径二到达迷宫出口仿真步数为36步,路径二为最优解,路径一为次优解。对于智能体来说,欲寻求最优路径,必须在到达上下均为悬崖的五角星位置二之后选择正确的向右动作后继续沿着右上侧的狭长小道运动才能到达迷宫出口;欲寻求次优路径,必须在到达上下均为悬崖的五角星位置一之后选择正确的向左动作后继续沿着左上侧的狭长小道运动才能到达迷宫出口。15*15迷宫环境相比于4*4迷宫环境难度大大提高,这对训练智能体将是一个不小的挑战。

使用1.2节Q-learning算法进行仿真,仿真过程中设置超参γ=0.9,ε=0.1,α=0.1,εdec=0.0001。仿真步数与累积奖励如图5所示。

图5 15*15迷宫环境下最终奖励与仿真步数图

我们将仿真次数提高至5000,智能体在如此多次训练后,累积奖励收益始终为0，即智能体始终无法成功通过路径一或者路径二走到迷宫出口,训练目标未达成。在这种状态-动作空间较大且为稀疏奖励的情况下,Q-learning算法训练表现差,即使投入极大的训练时间,也无法如愿达成训练目标。

2.2 奖励塑形

奖励塑形的核心就是应用先验经验及对环境的认知,合理设计奖励函数,引导智能体趋利避害,多快好省地达到训练目的。假定智能体在训练前已经对环境完全感知,即智能体详细掌握迷宫的出入口布局及悬崖分布情况信息,设计的势函数应该具备如下基本特性:

1)智能体距离迷宫出口sg越近,势函数的值越大,距离迷宫出口sg越远,势函数的值越小。势函数随距离增大梯度下降。

2)对智能体掉落悬崖设置惩罚,避免智能体掉落悬崖引起仿真中止。

考察函数φ(x)=1-x0.4x∈[0,1],φ(x)及其梯度曲线如图6所示。

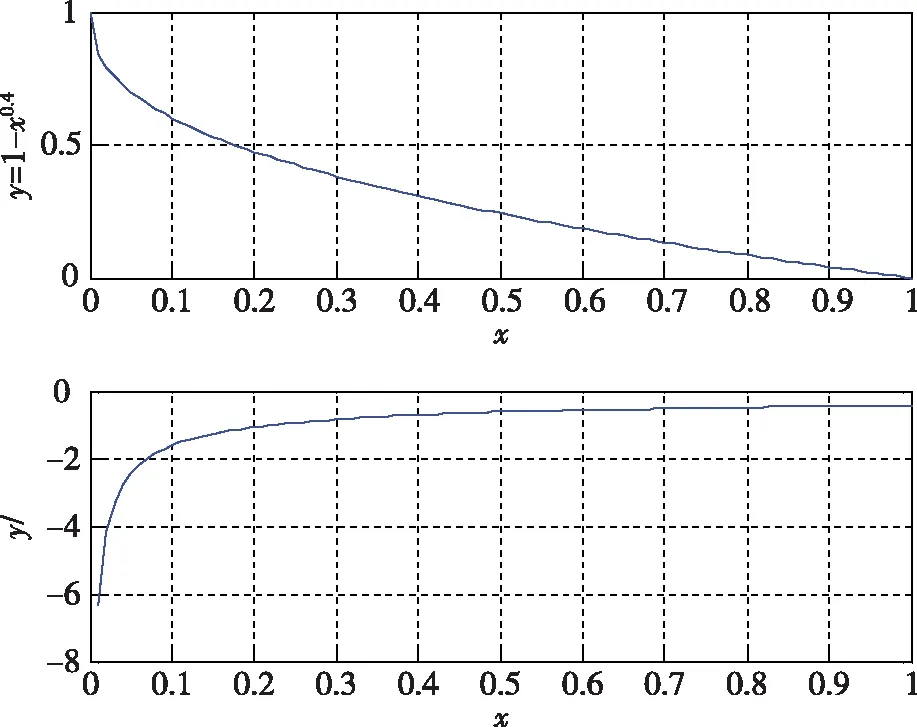
图6 函数φ(x)及导数曲线图

显然函数φ(x)满足势函数第一条基本特征要求。考虑势函数第二条基本特征要求对函数φ(x)进行修改,设计带惩罚项的势函数:

(15)

其中，dmax为所有d的最大值,d为当前状态s与终点状态sg之间的Manhattan距离,定义如下:

d=|x-xg|+|y-yg|

(16)

(x,y)表示当前状态s在迷宫中映射的坐标值,(xg,yg)为终点状态sg在迷宫中映射的坐标值。状态空间状态S={0,1,…,224}中任意状态s与迷宫中的坐标值映射关系描述为:

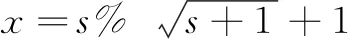
(17)

公式中，%为求余运算,∥为取整运算。

状态空间在迷宫中映射的坐标值如图7所示。

图7 坐标映射图

依据设计的势函数,可以得知15*15迷宫环境下势场分布图如图8所示(不考虑悬崖影响)。

图8 15*15迷宫环境下势场分布图

根据设计的带惩罚项的势函数构造奖励塑形函数:

F(s,a,s′)=γφ(s′)-φ(s)

(18)

将构造的奖励塑形函数F(s,a,s′)与原稀疏奖励叠加,得到一个重塑后的奖励函数:

R(s,a,s′)=F(s,a,s′)+R(s,a,s′)

(19)

2.3 改进的ε-greedy行为策略

我们在对仿真图5进行进一步分析能够发现,每一次仿真累积奖励始终为0且仿真步数都不足200步。这表明智能体结束一次仿真的原因是进行了不合适的探索导致不幸掉落悬崖。运用智能体对四周环境的感知能力,设智能体当前位置为s,其感知到的上下左右四个状态分别为sU,sD,sL,sR。对应的动作关系如图9所示。

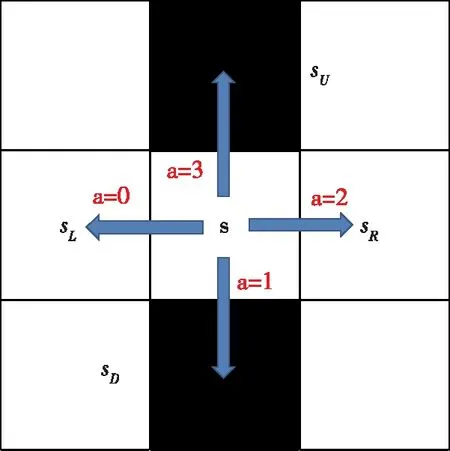
图9 动作空间的动作关系图

智能体感知四周环境,能够分辨出悬崖的状态集合SHOLE,进而得出使智能体下一步掉落悬崖的不合适的动作集合AHOLE,选择动作时在Aaction=A-AHOLE空间选择。如上图所示,可知SHOLE={sU,sD},AHOLE={1,3},Aaction={0,2}。基于此,设计改进的ε-greedy行为策略:

(20)

改进后的行为策略不再对不合适的行为进行探索,将有助于提高算法的收敛速度。

2.4 全感知条件下基于奖励塑形的Q-learning算法

全感知条件下基于奖励塑形的Q-learning算法采用改进的ε-greedy行为策略引导智能体对环境进行探索,使用重塑后的奖励函数鼓励智能体和环境交互。

3 试验仿真与分析

对全感知条件下基于奖励塑形的Q-learning算法进行仿真,为了突出改进的ε-greedy行为策略有效提升了算法的收敛速度,将其与改进前的ε-greedy行为策略(基于奖励塑形的Q-learning算法)进行对比仿真。设置超参数:γ=0.9,ε=0.1,α=0.1,εdec=0.0001。仿真结果如图10所示。

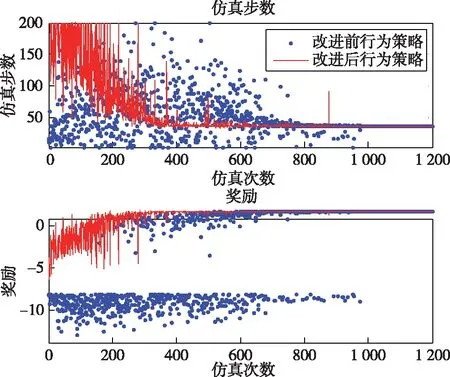
图10 全感知条件下基于奖励塑形的Q-learning算法对比仿真图

仿真结果表明:改进后的行为策略使智能体在400次训练后收敛,改进前的行为策略使智能体在1000次训练后才收敛。全感知条件下基于奖励塑形的Q-learning算法不仅能够使训练稳定收敛,而且改进的ε-greedy行为策略能够明显加快训练收敛速度,验证了本文所提算法的优越性。

4 结束语

经典Q-learning算法在解决状态-动作空间维数较大的稀疏奖励问题时存在训练效果差,有时甚至无法收敛的缺点。本文提出全感知条件下基于奖励塑形的Q-learning算法。主要工作内容有:

1)对本文采用的15*15迷宫环境进行介绍,分析经典Q-learning算法确实无法令训练收敛；

2)假定智能体对环境完全感知,设计带惩罚项的势函数构造奖励塑形函数；

3)考虑智能体对四周环境的感知能力,提出改进后的ε-greedy行为策略；

4)提出全感知条件下基于奖励塑形的Q-learning算法,并进行仿真。

通过对比仿真试验,全感知条件下基于奖励塑形的Q-learning算法在解决状态-动作空间维数较大的稀疏奖励问题时可以稳定收敛且显著提升了收敛速度。

本文在构建奖励塑形函数时假定智能体对环境有全局感知能力,实际情况下智能体一般仅能对四周有限范围具备感知能力,有限感知条件下的奖励塑形强化学习算法是后续研究的方向。