InSAR与概率积分法联合的矿区地表沉降精细化监测方法

陈洋，陶秋香，刘国林，王路遥，王凤云，王珂

山东科技大学 测绘与空间信息学院，山东青岛 266590

0 引言

煤炭作为重要的能源基础，是工业现代化和社会发展的有力支撑.但随着能源需求的日益提升，煤炭开采在为世界经济创造巨大价值的同时，其引发的灾害问题也不容忽视：矿区大规模持续开采造成的沉降、塌陷，不仅损害地面基础设施，还容易诱发各种地质灾害，对人民财产安全造成巨大威胁(Yang et al., 2019; Saedpanah and Amanollahi, 2019; Sahoo and Khaoash, 2020).因此，为预防灾害发生，保证安全生产，必须对矿区进行长期有效的沉降监测与防治.

合成孔径雷达干涉测量(Interferometric Synthetic Aperture Radar, InSAR)是一种地面沉降监测新技术，可监测到厘米级甚至毫米级的地面变化，是探测地震、火山、矿区等形变的有效工具(Klein et al., 2017; 韩宇飞等, 2010; 申文豪等, 2019).20世纪90年代，该技术开始用于矿区地表沉降监测，所获结果在空间、时间上均连续，并且可以很好地反映矿区沉降的结构特征(Raymond and Rudant, 1997).相较于精密水准、GPS等传统测量手段，InSAR表现出全天候、低成本等的独特优势，为矿区地面沉降监测提供了新的思路与技术支持(Yang et al., 2018; Liu et al., 2013).但矿区开采引起的地面沉降往往呈现沉降速度快、量值大，空间不连续等特征，InSAR技术受限于SAR影像的固定特性，在下沉较为严重的沉降盆地中心会出现失相干现象，无法得到准确的形变信息，很大程度上限制了该技术在实际工程中的推广应用(Luo et al., 2019; Carlà et al., 2018; Zhang et al., 2020).

为解决InSAR监测矿区大梯度沉降时出现的失相干问题，国内外学者首先从技术本身出发，通过减少对流层延迟、选取长波段数据等方法提升InSAR的大梯度沉降监测能力，后又结合实际地质模型展开进一步的研究与探索，其中概率积分法是应用最为广泛的一种矿区沉降预计模型(Xu et al., 2006; Wang et al., 2020; Ge et al., 2007; 陶秋香等, 2012; Fan et al., 2014).该方法是由我国学者刘宝琛、廖国华等基于随机介质理论提出的一种沉降预计方法，利用高精度监测点，通过选定适当的数学模型，完成参数优化反演，获取沉降中心的下沉信息，有助于解决InSAR在矿区大梯度沉降监测中的失相干问题(刘宝琛和廖国华, 1965; 刘宝琛和戴华阳, 2016).但该方法由于受到模型自身特性的限制，在沉降边缘处收敛过快，尤其模型通常依赖成本高、耗时多的水准数据，导致其在矿区沉降监测中仍存在一定的局限性.

综合InSAR与概率积分法在矿区地表沉降监测中的优缺点，本文联合InSAR与概率积分两种监测方法，获取准确的矿区沉降盆地.该方法首先选取覆盖矿区工作面的SAR影像集，利用InSAR技术，按照时间序列两两差分，并对其进行时序累积，获取矿区多时段累积沉降监测结果；然后基于相干性条件，选取InSAR沉降盆地边缘的高相干点，与沉降中心附近少量插值后的水准数据作为特征点，通过曲面拟合法对概率积分模型参数进行优化反演，得到概率积分预计的矿区地表沉降盆地；进而以相干性为基准，通过形变梯度理论确定两种监测结果的融合阈值，获取完整的沉降盆地.论文以山东某矿区为研究区，利用该方法获取矿区地表沉降信息，结果表明，该方法结合了InSAR与概率积分法的优势，既能反映矿区开采对周边环境的影响，又能提取沉降中心准确的地表下沉信息，实现矿区沉降的高效、准确提取.

1 基本原理

1.1 InSAR形变监测及最大形变梯度

实际观测中，InSAR获取的相位与雷达参数、天线位置、天线入射角及地面目标高程紧密相关，干涉过程中不可避免会受到各种误差因素的影响，导致干涉相位信息中不仅包含高程和形变信息，还存在其他干扰项(Massonnet and Feigl, 1998)，即

φ=φflat+φtopo+φdef+φatm+φnoise,

(1)

由式(1)可以看出，InSAR获取的相位信息主要包括：平地相位φflat，地形相位φtopo，地表形变相位φdef，电离层延迟和对流层延迟引起的大气相位φatm以及噪声相位φnoise.显然，要想获取地表形变相位，必须将干扰相位从干涉图中分离.

当去除各类干扰后，其形变相位在干涉图中表现为一系列干涉条纹，且干涉条纹所包含的相位信息并不是绝对相位，而是各个像元之间的相对相位.为此，Massonnet和Feigl(1998)提出形变梯度的概念，用以代表任意两点间的相对位移，并给出了 InSAR 可监测的最大形变梯度为

(2)

式中，dmax表示InSAR理论上能够监测到的形变梯度最大值，μ表示单个SAR影像像元的尺寸，λ表示雷达波长.由式(2)可见，dmax理论上与雷达本身参数有关，雷达波长越长、单位像元越小，能够监测到的形变梯度越大.以多视处理后的C波段Sentinel(分辨率为20 m)和L波段 ALOS(分辨率为10 m)数据为例，经过1∶4多视处理的Sentinel影像，理论上能监测到1.4×10-3的形变梯度，而经过1∶3多视处理的ALOS影像，理论上能监测到11.5×10-3的形变梯度.

式(2)是假定理想条件下，InSAR能监测到的最大形变梯度.然而在实际情况中，InSAR不可避免地会受到轨道误差、时空失相干、大气延迟效应等的影响，最大形变梯度监测值往往比理论值要小.针对这一现象，Baran等(2005)分析研究了相干性对InSAR技术形变梯度的影响，给出了以影像相干性为基准的形变梯度阈值表达式，即

Dmax=dmax+0.002(γ-1),

(3)

式中，Dmax为实际InSAR最大可监测形变梯度，γ为影像相干性.由式(3)可以看出，InSAR可监测最大形变梯度与影像相干性呈线性正相关，相干性越高，实际可监测最大形变梯度越大.对于SAR影像，一般存在某一相干阈值，使得Dmax=0.例如，对Sentinel影像，相干系数γ=0.3时，Dmax=0，即对于Sentinel数据来说，当影像相干性小于0.3时，就无法监测到地表形变.通常情况下，矿区常常具有植被覆盖率高、短时间内形变量值大的特点，为了更为有效地提取形变信息，在矿区利用InSAR技术进行地表沉降监测往往对相干性有着更高的要求.

1.2 概率积分模型

开采沉降研究中的岩体往往成因复杂，由于各类地质作用，使得岩体生成过程中被各种断层、节理等不均匀介质切割，产生一系列次生裂隙及非连续面，而矿山开采会再次扰动岩体的原生结构，呈现出更加明显的非连续性，因此非连续介质模型更适合开采沉降的应用研究.20世纪50年代，Litwiniszyn(1956)基于非连续介质模型，首次提出随机介质理论，并将其用于岩层移动规律的研究，认为随机介质的颗粒介质模型可用来描述由于矿山开采引发的地下岩层及地表移动规律.20世纪60年代，我国学者刘宝琛和廖国华(1965)在此基础上提出概率积分法，该方法将矿山岩层移动看作一个服从正态分布的随机现象，结合概率密度函数模拟地表沉降盆地的形态.对于走向长为D3、倾向长为D1的工作面，其开采引发的地面任意点(x,y)的沉降值可表示为

(4)

其中：

(5)

式(4)、(5)均在工作面坐标系下，其中W0表示最大下沉值，W0(x)、W0(y)分别表示待求点在走向、倾向主断面上投影点的下沉值，u表示概率积分的开采单元，m为煤层厚度，H0为平均开采深度，H1、H2分别为下山、上山开采深度，q为下沉系数，tanβ为主要影响角正切，tanβ1、tanβ2分别表示下山、上山主要影响角正切，S3、S4分别表示左右边界的拐点偏移距，S1、S2分别表示下山，上山拐点偏移距，θ为开采影响传播角.

1.3 InSAR与概率积分法联合的矿区地表沉降监测方法

InSAR技术是获取矿区沉降的高效手段，能够准确获取沉降的边缘信息，但由于SAR影像自身特性的限制及各种噪声误差的干扰，该技术在矿区沉降量大的中心区无法探测到准确的沉降信息，监测结果与实际情况相差较大.概率积分法在沉降盆地中心具有较高的监测精度，但开采煤层容易受外力影响产生裂缝，加大煤柱上覆岩层的变形，导致概率积分法预计的沉降盆地边缘收敛过快，在沉降边缘的监测精度降低(王正帅和邓喀中, 2012).综合InSAR与概率积分法两种方法的沉降监测优势，可以获取准确完整的矿区地表沉降信息.其具体步骤如下：

(1)选取覆盖矿区的N+1景SAR影像，按照时间序列对其进行两两差分处理，得到N个干涉对，并通过时序累积，获取矿区时序形变信息dInSAR.

(2)收集矿区实际资料及工作面水准监测数据，考虑到水准点高程值在各个监测时段内近似呈线性变化，对其进行时间域上的分段线性插值，实现InSAR与水准在时间上的统一，预测出SAR成像日期下，各水准点的实际沉降信息，即

(6)

式中，dlevling表示水准点在SAR成像日期下的沉降信息，Tlevling表示水准点观测日期，TInSAR、T′InSAR分别表示距水准点观测日期最近的前后两个SAR成像日期，dInSAR、d′InSAR为这两个SAR成像日期下该水准点的InSAR沉降监测结果.

(3)选取InSAR沉降盆地边缘的高相干点，与沉降中心附近少量插值后的水准数据作为特征点，并将其投影至工作面坐标系.假设坐标为(x,y)的特征点的沉降为D(x,y)，则按照曲面拟合法可将其表示为一个与特征点坐标(x,y)及概率积分预计参数B有关的函数，即

D(x,y)=f[(x,y);B],

(7)

用DZk(k=1,2,…,n)表示各特征点对应的实际沉降，并使曲面拟合值D(x,y)与实际监测结果的偏差满足平方和最小，即

(8)

式中，V为各特征点实际监测值相对于最小二乘拟合值的偏差.从而即可得到矿区概率积分参数的反演结果为

B=[q;tanβ;tanβ1;tanβ2;S3;S4;S1;S2;θ].

(9)

(4)根据反演的概率积分参数，按照式(4)、(5)，建立矿区概率积分沉降模型，并将沉降结果转换至地理坐标系下.进一步利用克里金插值法，对区域化沉降进行最优估计，获取连续的概率积分沉降结果dPIM.

(5)统计N个干涉对的相干情况，计算其平均相干系数γavg，根据式(3)得到该相干条件下InSAR可监测到的最大形变梯度Dmax.基于形变梯度理论，考虑到Sentinel-1A影像的分辨率是20×20 m，可以计算得到N个干涉对能监测到的最大形变量dmax|InSAR(Massonnet and Feigl, 1998)，即

dmax|InSAR=μ·Dmax·N,

(10)

将dmax|InSAR作为InSAR与概率积分法沉降结果融合的阈值，从而得到完整的矿区地表沉降盆地，即

(11)

其数据处理流程如图1所示.

图1 InSAR与概率积分法联合的矿区沉降监测数据处理流程

2 研究区及数据源

2.1 研究区概况

试验选取山东某矿区为研究区域，其地理位置及范围如图2a所示.矿区地属黄河冲积平原，地形平坦，地面标高+40.53～+45.89 m，自然地形坡度为0.01%.矿区内交通便利，与邻近各县、乡均有公路相通，且有兖新铁路、220国道在其南部通过.区内河渠众多，主要有宋金河、鄄郓新河、郓巨河等，水源丰富，地表以植被为主.区内村庄众多，人口稠密，因此对于矿区来说，一方面要保证开采安全，另一方面，又要考虑到周边建筑、道路等地物的保护问题.同时兼顾矿区安全开采和地面维护，完成高效率、低损耗的生产，迫切需要有效的矿区地面沉降监测.

图2b中白色矩形表示该矿区1301工作面的开采范围，该工作面上覆地表主要以植被为主，西北部为已开采的1300工作面老采空区，且有宋金河、郓城新河自其上方穿过.工作面平均煤厚6.8 m，自2016年10月开始开采，倾斜宽223.4 m，计划开采长度2265.8 m，至2018年3月，工作面推进1385.6 m，平均开采深度为938 m，地面标高为+41.8～+44 m.图2(b)中绿色标记点表示工作面上方的水准点，沿倾向线自西向东布设有H1～H69，共69个水准点，沿走向线自南向北布设有Z1～Z92，共92个水准点，测量工作自2016年10月16日开始，至2018年3月24日结束，共19期.

图2 研究区地理范围

2.2 数据源

哨兵1号(Sentinel-1)卫星于2014年4月成功发射，载有C波段合成孔径雷达.该卫星在轨运行高度为693 km，数据更新周期为12天，是一个可实现时间、空间连续观测的雷达成像系统，实现了单、双极化等若干种不同的极化方式.可提供连续影像(白天、夜晚和各种天气)，以其大范围、多模式、多应用的特点为更多用户提供了数据服务.为获取矿区的地面沉降情况，本试验选取覆盖矿区的21景C波段、VV极化的Sentinel-1A升轨数据(成像中心入射角约为38.92°)，时间跨度为2016年10月16日—2018年3月4日.具体参数如表1所示.

表1 SAR影像参数

InSAR技术需要通过外部数字高程模型(DEM)模拟地形相位，并将其从SAR干涉相位中移除，以提取地表沉降相位和沉降值.由于研究区域地形平坦，实验选取3*3弧秒的SRTM3 DEM，可以满足矿区地面沉降监测的精度需求.SRTM3 DEM数据的采集间隔为3弧秒，地面分辨率为90 m，平均精度为16 m.

3 联合法提取的矿区地表沉降结果及分析

3.1 InSAR矿区沉降监测

将表1中的20个干涉对按照时间序列进行两两差分处理，考虑到干涉相位不可避免会受到多种噪声的影响，利用自适应滤波方法进行噪声去除，得到滤波后增强的差分干涉相位及相应的相干系数图，如图3、图4所示.

图3 滤波后的差分干涉图示例

图4 相干系数图示例

由图3可见，矿区在监测初期，干涉条纹较少，之后随着时间推移，矩形区域内干涉条纹变得密集，因而判定该区域在研究时段内可能发生地面沉降.结合图4可知，第18、19个干涉对在监测时段内，相干性较好，相应的差分干涉图中显现出清晰完整的干涉条纹；相比而言，第9、12个干涉对噪声较大，出现严重的失相干，这是由于夏季植被覆盖率较高或沉降梯度过大，超出影像的实际监测能力导致的，对比此时的差分干涉图，在沉降区域，干涉条纹杂乱，甚至未形成完整的条纹形状.

将滤波增强后的差分干涉相位进一步进行解缠处理，并将解缠后的真实相位转换成雷达视线向上的地表形变值，并通过投影、地理编码得到地理坐标系下垂直向上的真实形变量.为了实现研究区域时序沉降盆地的监测，假设起始监测日期2016年10月16日无形变发生，将InSAR监测结果进行时序累加，得到2016年10月16日—2018年3月4日期间各成像时刻的累积沉降结果，如图5所示.

图5 InSAR累积沉降结果

由图5分析可以得到，1301工作面自2016年10月开始开采，至2016年12月，InSAR监测到工作面起采线附近开始出现漏斗状的沉降盆地，说明此时工作面的开采活动已对上覆地表产生影响.但由于开采时间较短，沉降量较小，截至2016年12月3日，InSAR监测到的最大累积沉降为22 mm.随后，由于开采工作面的持续推进，矿区沉降范围及沉降量相对于监测初期而言，明显增大，至2017年6月1日，InSAR监测到的累积沉降达到225 mm.随着工作面持续向北推进，监测结果显示沉降中心开始沿工作面走向逐步向北移动，至2017年11月28日，监测到的沉降中心距离起采线约160 m，最大累积沉降为420 mm.由此可见，InSAR监测到的沉降位置、范围及空间变化趋势与矿区实际开采工作面相符，但在沉降中心处的大梯度沉降监测能力明显不足.随着工作面的持续开采，矿区沉降继续加大，至2018年3月4日，水准监测到工作面最大累积沉降达到2813 mm，而InSAR监测到的最大沉降仅为548 mm，与矿区实际存在较大差异.

3.2 特征点选取

为了构建概率积分模型，进一步提取InSAR沉降结果中的高相干特征点.由InSAR监测最大形变梯度式(3)可知，对于Sentinel-1A SAR影像来说，当相干性系数小于0.3时，InSAR监测结果是不可信的.在实际情况中，由于矿区短时间内沉降过大，其监测精度对相干性有更高的要求.因此，根据图4矿区的相干情况，这里将0.5作为相干性阈值，认为相干性大于0.5的特征点为高相干点，提取InSAR沉降盆地边缘的13个高相干点，并根据概率积分原理，选取临近矿区最大沉降点和拐点的5个水准点，共18个特征点，其叠加在工作面的分布情况如图6所示.表2给出了各点的相干性系数及沉降信息.

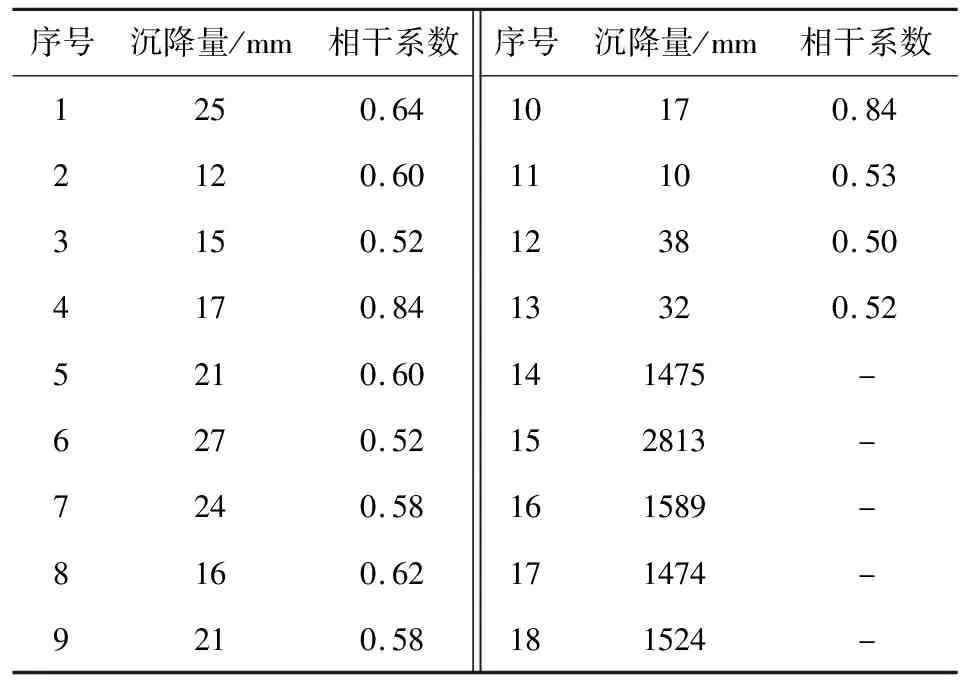
表2 特征点相干系数及沉降信息

图6 特征点分布图

3.3 概率积分沉降预计

结合选取的18个特征点和概率积分模型，利用曲面拟合法，反演得到该矿区的概率积分参数为

B=[q;tanβ;tanβ1;tanβ2;S3;S4;S1;S2;θ]

=[1.3;1.2;1.9;1.6;47.5;47.5;34.6;34.6;84.6°]

将这些参数代入式(4)，计算得到矿区1301工作面的概率积分沉降预计盆地，如图7所示.为获取连续的概率积分地面沉降，考虑到Sentinel-1A影像分辨率为20×20 m，在矿区1301工作面沉降盆地处，以20 m为间隔共选取18396个特征点，计算其沉降值，并将结果转换至地理坐标系下，进一步利用克里金插值法，对区域化沉降进行最优估计.图8给出了插值后空间连续的概率积分矿区沉降结果.

由图7、图8可以看出，研究时段内，概率积分法探测到1301工作面上方呈现明显的漏斗状沉降盆地，最大沉降为2528 mm.但该方法测得工作面周边几乎无沉降发生，沉降盆地在边缘处收敛过快，其原因是在实际情况下，矿区沉降往往存在复杂地形、地下水流失及其他采空区开采等外部因素的影响，而概率积分模型仅考虑开采活动引发的地面沉降，导致其监测到的地面沉降集中在工作面上方.

图7 概率积分矿区沉降预计盆地立体图

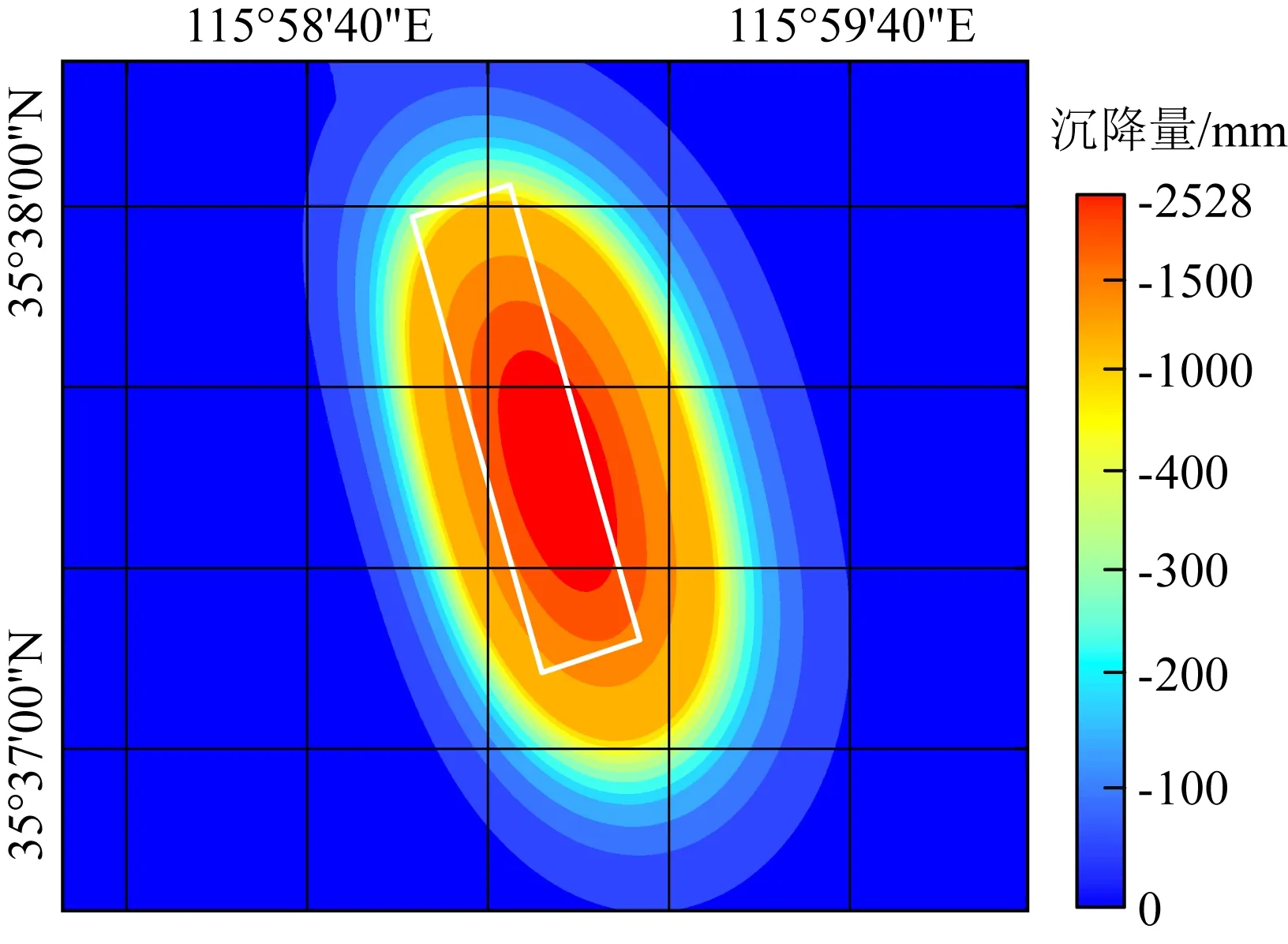
图8 连续的概率积分沉降结果

3.4 联合法提取完整的矿区地表沉降盆地

对图4所示矩形区域内的相干系数结果进行均值滤波处理，并统计20个干涉对中沉降区域的相干情况，统计结果如表3所示.分析表3可知，2016年10月16日—2018年3月4日期间，矿区沉降区域的相干性为0.39～0.64.其中夏季4—8月，为农作物生长时节，植被覆盖率高，获取的SAR影像相干性普遍较差，秋冬季节SAR影像质量相对较好.

根据表3各干涉对的相干结果，计算得到研究时段内20个干涉对的平均相干系数γavg为0.502.结合式(3)、式(10)，考虑到Sentinel-1A的影像分辨率为20×20 m，进一步计算得到此时InSAR能监测到的最大形变量dmax|InSAR为162 mm.以此为阈值，对InSAR沉降边缘和概率积分沉降中心结果进行融合，得到矿区完整的沉降盆地，其结果如图9所示.

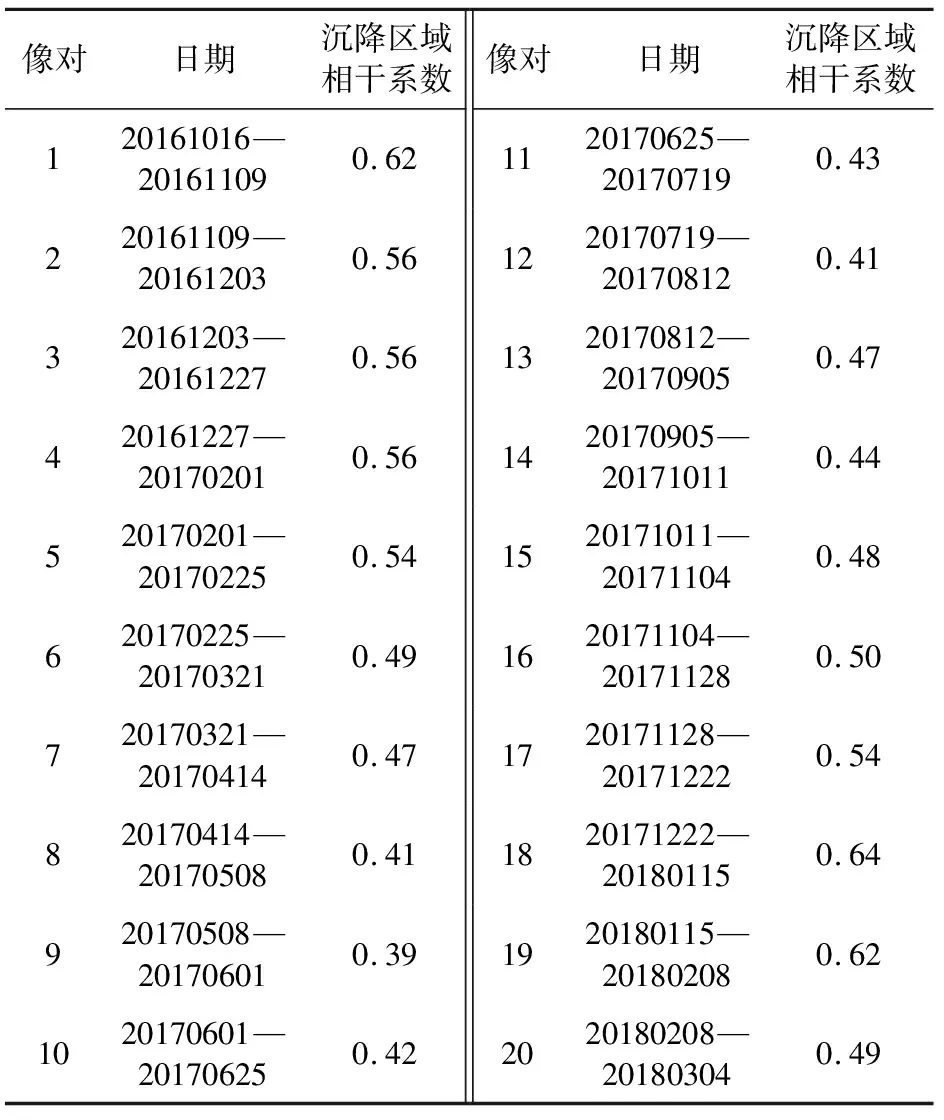
表3 矿区20个干涉对的相干系数统计

由图9可以看出，InSAR与概率积分法通过融合，可以得到矿区完整的沉降结果，但在融合的边界却出现结果的不连续现象.为解决这一问题，本文在融合边界的两侧寻找一定区域内的InSAR与概率积分法预计的沉降数据，对其进行加权平均.

图9 联合法沉降监测结果

由InSAR监测结果可知，20个干涉对的平均相干系数γavg为0.502，但处于夏季的干涉对干涉效果差，相干性低，其相干系数低于平均相干系数，监测精度较低.因此，在加权平均中，选择相干性大于平均相干系数γavg的第1、2、3、4、5、17、18、19个干涉对，计算其平均相干系数为0.58.在该相干条件下，结合式(3)、式(10)，考虑到Sentinel-1A的影像分辨率为20×20 m，计算得到此时InSAR能监测到的最大形变量为90 mm.以此作为加权平均的下临界阈值，当沉降量小于90 mm时，以InSAR监测值作为最终沉降结果.

对于概率积分法而言，拐点通常位于沉降盆地主断面上沉降曲线曲率为零的分界点，根据概率积分预计的沉降结果，以工作面走向起采线与终采线处概率积分沉降结果的平均值917 mm作为加权平均的上临界阈值.当沉降量大于917 mm时，以概率积分预计的沉降值作为最终沉降结果.

当沉降量介于90 mm到917 mm时，通过对InSAR与概率积分预计的沉降值进行加权平均，确定最终沉降结果.首先选择沉降量介于90～917 mm的水准点，共48个，计算其InSAR、概率积分法沉降结果与水准的绝对差值，如图10所示.然后计算48个水准点InSAR监测结果、概率积分法预计结果的累积均方差，分别为186 mm、208 mm.根据

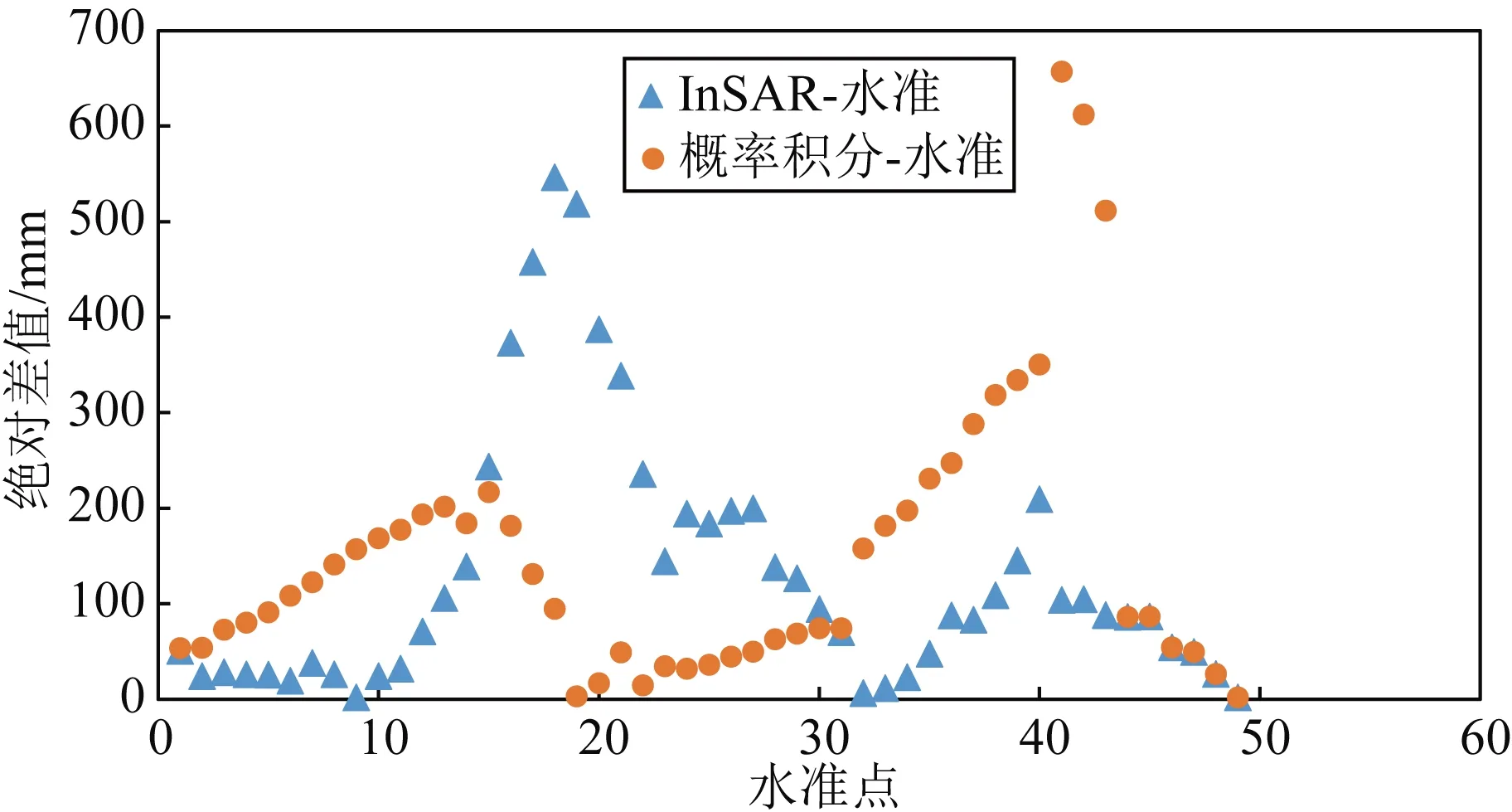
图10 部分水准点的误差情况

(12)

计算得到PPIM=0.8PInSAR.这里取PPIM=0.44，PInSAR=0.56，则由

(13)

得到加权平均后完整的矿区沉降盆地，如图11所示.

图11 加权融合后的联合法沉降监测结果

由图11可知，2016年10月16日—2018年3月4日期间，联合法监测到矿区出现地面沉降，且沉降盆地位置与矿区1301工作面高度吻合.研究时段内，该方法监测到工作面周边存在小量级沉降，这是因为工作面附近存在一系列小断层，开采工作的持续推进，扰动了其上覆岩层，产生微小形变，对周边环境造成不同程度的影响，与矿区实际开采进度及地质情况相符，说明该方法在沉降盆地边缘的监测效果优于概率积分法.由联合法在沉降盆地中心的监测结果分析可以得到，截至2018年3月4日，该方法监测到1301工作面的沉降中心位于距离起采线约600 m处，沉降中心向东部偏移，这主要是因为1301工作面存在约10°的地面倾斜，沉降中心向下山方向偏移，与矿区实际情况相符，其监测到的最大累积沉降达到2528 mm，在沉降中心的监测能力明显优于InSAR手段.

4 联合法监测结果精度评估

为进一步验证联合法监测结果的精度，提取矿区1301工作面倾向线上H1～H69，走向线上Z1～Z92，共161个水准点的联合法监测结果、InSAR累积沉降、概率积分法预计沉降，并收集实际水准测量数据，对三种监测方法的测量结果进行定量对比分析，图12给出了对比结果图.以InSAR能监测到的最大形变量dmax|InSAR=162 mm为区分沉降盆地边缘和中心的阈值，分别统计三种监测方法在沉降盆地边缘和中心的误差，表4给出了三种监测方法的误差对比情况.

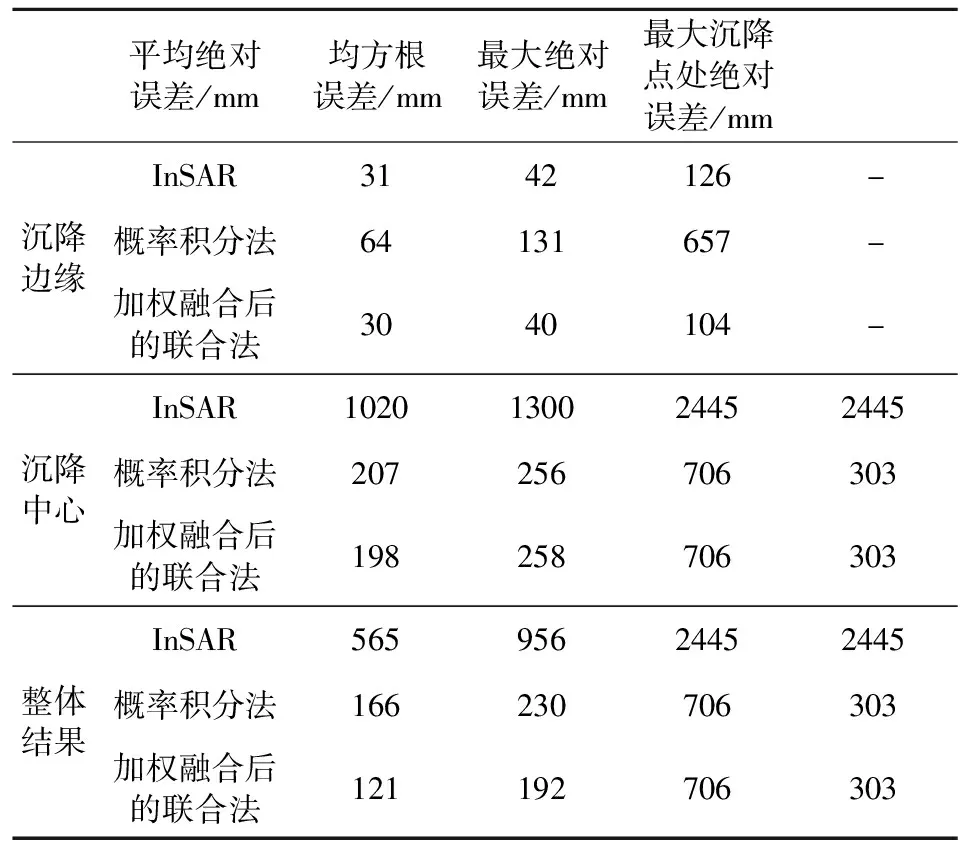
表4 误差统计

由图12、表4三种监测方法的对比结果，分析可以得到：

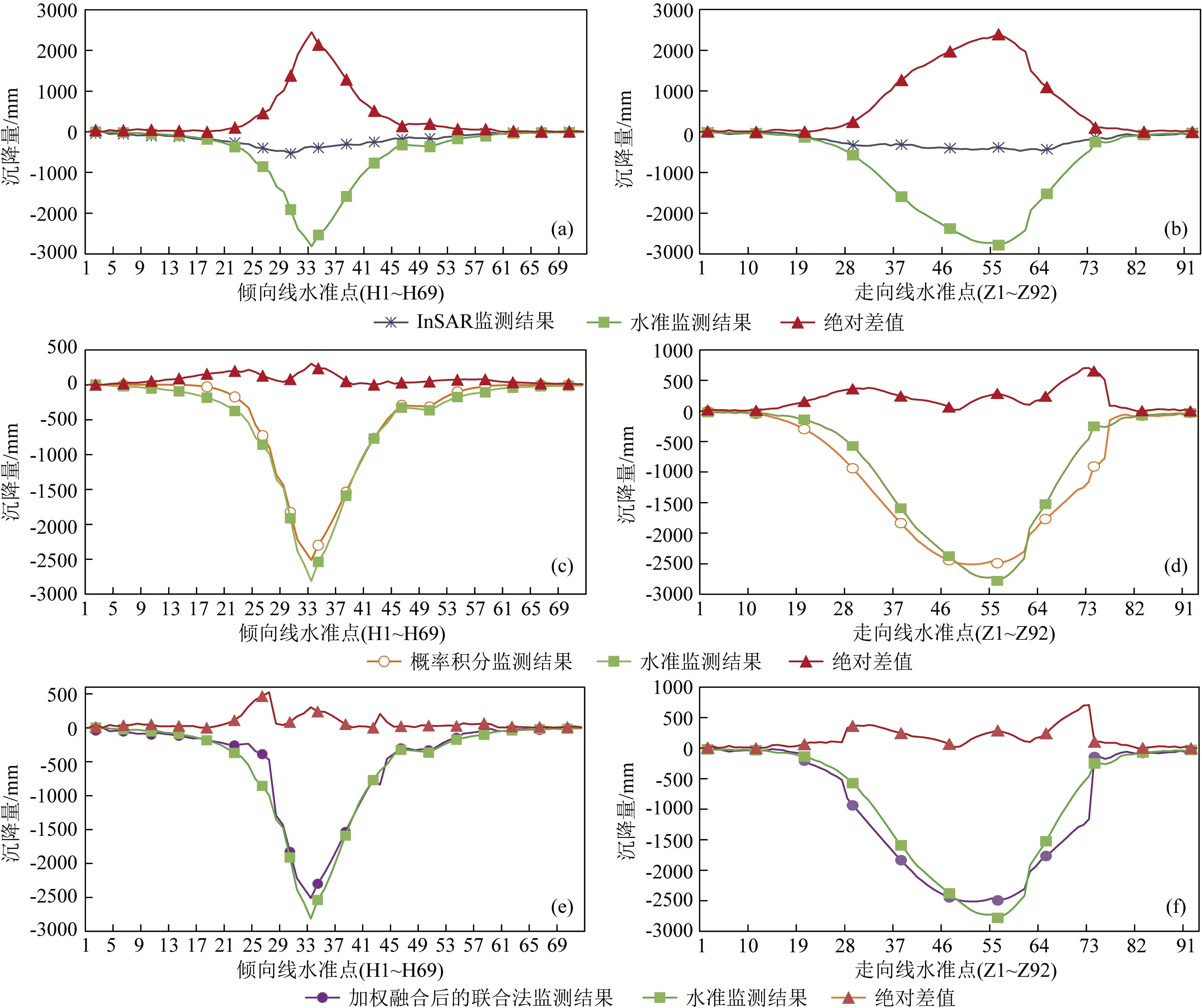
图12 监测结果对比图

(1)2016年10月16日至2018年3月4日期间，联合法、InSAR和概率积分法均探测到1301工作面上方出现地面沉降，监测得到的沉降盆地位置、沉降曲线形态及变化趋势基本一致，且与水准监测结果相符.

(2)通过与概率积分法结果对比，联合法在沉降边缘处与水准吻合程度更高.分析图12(c)、(e)中二者在倾向线上的监测结果可以得到，在沉降边缘处，由于1301工作面西部存在小断层，受其影响，导致沉降范围向西部扩大，联合法监测到这一沉降趋势，在H1～H23范围内，其测得的沉降曲线与水准吻合较好.对比此时概率积分法的监测结果，发现该方法探测到的沉降范围略小，沉降曲线在边缘处收敛较快，分析是由于概率积分法在反演过程中并未考虑外部条件对沉降的影响，造成该方法对于受到断层影响而引起的沉降不敏感.分析图12(d)、(f)中走向线上二者的沉降曲线同样发现，在沉降盆地的边缘区域，联合法可以获得与实际更相符的监测结果.在沉降边缘处，联合法监测结果的平均绝对误差为30 mm，均方根误差为40 mm，最大绝对误差为104 mm，相比概率积分法而言，三种误差分别提升53%、69%和84%.

(3)通过与InSAR结果对比，联合法在沉降中心处的大梯度监测能力明显提升.图12(a,e)二者的监测结果显示，水准监测到倾向线上32点处出现2813 mm的最大沉降.InSAR虽也探测到此处为沉降中心，但监测到的最大沉降点与水准略有差别，出现在29点处.监测结果与水准相比，最大绝对误差达到2445 mm，这主要是由于矿区沉降中心沉降梯度过大，超出Sentinel-1A影像的实际监测范围，加上地表植被、噪声等降低了SAR影像质量，导致其在沉降中心处无法探测出真实的沉降信息.对比联合法获得的沉降结果可以看出，在沉降中心处，该方法监测结果与水准吻合较好，其监测得到的最大沉降点也与水准结果一致，监测到的最大累积沉降为2510 mm，与水准相差303 mm.图12(b,f)为走向线上两种技术在沉降盆地中心的监测结果，表现出与倾向线上相同的特征，InSAR与联合法监测到的最大沉降分别为469 mm和2510 mm，与水准的最大绝对误差分别为2396 mm和706 mm.在沉降中心处，联合法监测结果的平均绝对误差为198 mm，均方根误差为258 mm，最大绝对误差为706 mm，最大沉降点处的绝对误差为303 mm，相比InSAR而言，四种误差分别提升81%、80%、71%和88%.

(4)根据三种监测方法的误差统计分析可知，矿区倾向线、走向线上所有水准点的联合法监测结果的平均绝对误差为121 mm，均方根误差为192 mm，最大绝对误差为706 mm，最大沉降点处的绝对误差为303 mm.相比InSAR和概率积分法而言，整体监测精度有所提升，四种误差相较于InSAR分别提升79%、80%、71%和88%，平均绝对误差与均方根误差相较于概率积分法分别提升27%和17%.

5 结论

本文针对InSAR和概率积分法目前各自监测矿区地表沉降存在的不足，基于影像相干性及InSAR形变梯度理论，提出了两种技术联合进行矿区沉降监测的方法.以山东某矿区1301工作面为研究区，利用该方法进行沉降监测，获取了研究时段内矿区沉降盆地.通过与同期水准实测数据、InSAR累积沉降和概率积分监测结果进行对比分析，得出如下主要结论：

(1)联合法相比概率积分法而言，在沉降盆地边缘的监测精度有所提升，可以在减少水准观测的基础上，很好地避免模型本身的缺陷.该方法在沉降边缘处与水准的平均绝对误差、均方根误差和最大绝对误差相较于概率积分法分别提升53%、69%和84%，可以解决概率积分法在矿区地表沉降监测中收敛过快的问题，监测结果与水准更为吻合.

(2)联合法相比InSAR技术而言，在沉降盆地中心的监测能力明显提升.该方法在沉降中心处的平均绝对误差、均方根误差、最大绝对误差和最大沉降点处的绝对误差相较于InSAR分别提升81%、80%、71%和88%，能够有效弥补InSAR在监测矿区大梯度地表沉降时的不足.

(3)联合法结合InSAR与概率积分法各自的优点，可以准确探测出矿区沉降盆地的位置、范围及沉降变化趋势，反映矿区开采对周边环境的影响，且监测得到的沉降中心符合矿区开采的地表移动规律，能够提取沉降中心准确的下沉信息.相比概率积分法和InSAR技术而言，该方法的整体监测精度有所提升，可以获得与实际情况更为吻合的地表沉降.

致谢感谢欧洲航天局(European Space Agency, ESA)提供免费的Sentinel-1A SAR数据和美国国家航空航天局(National Aeronautics and Space Administration, NASA)提供SRTM3 DEM数据.