基于等效刚度仿真应力的螺钉强度校核*

丁承文，向华平

（南京电子技术研究所，江苏南京210039）

引 言

螺纹连接是一种可拆卸的固定连接，特点是结构简单，连接可靠，装拆方便。螺钉是螺纹连接的主要形式之一，螺钉直接旋入到被连接件的螺纹孔中，省去了螺母环节，具有结构简单、单侧连接、维修空间需求小的突出优势，在航空电子产品结构件中应用广泛。

航空电子设备安装在飞机平台上，需要耐受振动、冲击、过载等载荷，力学环境恶劣。螺钉作为航空电子设备与载机间重要的连接功能件，其强度与寿命设计是否合理直接关系到平台的安全性，显得尤为重要。

螺钉连接结构存在的接触和预紧力等非线性因素对有限元计算结果影响较大。国内外专家学者对螺钉连接结构进行了大量的数值模拟计算和实验研究。对螺钉连接结构进行模拟计算时，普遍采用三维实体建模法，并对螺钉模型进行细致的网格划分，以确保数值计算的准确性[1–3]。但是，对于复杂机械结构，装配时会使用大量螺钉进行连接。螺钉数量的增加导致数值模拟计算量随之显著增大，计算速度明显降低。因此，有必要对螺钉模型进行合理简化，从而提高多螺钉连接模型的计算效率，以满足工程快速迭代的需求[4]。

本文以某电源机箱与安装板连接为例，通过等效刚度模型对螺钉进行简化处理，建立系统有限元模型，仿真得到电源机箱与安装板之间螺钉的三向载荷。按照第四强度理论，对螺钉进行强度和寿命校核，校核其工程合理性。

1 工程背景介绍

电源机箱（图1）是某航电设备的重要组成部分，外形尺寸为500 mm×350 mm×195 mm。根据结构承载特点，电源机箱采用框架结构整体焊接成形，提高了单元机箱的整体刚度，降低了连接部位的应力水平。

图1 电源机箱的几何模型

电源机箱采用过渡安装板与飞机骨架进行转接，其中电源机箱通过整体拆装方式进行维护，安装板则常驻于飞机骨架，从而提升电源机箱的维修便捷性。

电源机箱与安装板之间通过左右两侧8–M8的螺钉进行紧固连接。由于电源机箱高度达195 mm，连接螺钉必然承受较大的弯矩载荷，因此螺钉尽量排布于机箱远端两端。同时为了最大程度地均衡各点的应力水平，螺钉排布的几何中心与设备的几何重心重合，分布间距按照刚度原则进行设计[5–6]，具体布置见图2。

图2 连接螺钉排布

2 螺钉等效刚度计算

电源机箱与安装板之间的连接螺钉选择GB70型内六角螺钉，螺钉的材料为30CrMnSiA，电源机箱底板与安装板材料均为5A05（H112）铝合金，两者的弹性模量相同。

为获得上述连接螺钉的轴向刚度，将电源机箱底板与安装板的压力分布简化为空心圆柱体分布，认为在任意垂直于螺钉轴线截面方向上的压应力满足均匀分布。基于上述等效简化，螺钉的轴向刚度可以表示为：

式中：dh为螺钉孔直径；dw为垫圈直径；L为连接处电源机箱底板加安装板的厚度，L=ts+tx（ts为电源机箱底板连接部位厚度，tx为安装板连接部位厚度）；θ为安装板连接部位压应力分布的半顶角；E1为电源机箱底板或安装板的弹性模量[7]。

为获得螺钉的剪切刚度，将电源机箱底板和安装板之间的连接形式等效为搭接形式，同时将螺钉的承载极限限定在线弹性范围内。基于以上假设，螺钉的剪切柔度可以表示为：

式中：d为螺钉直径，由于是铰制孔，d=dh；E为螺钉的弹性模量；G为螺钉的剪切模量；Ejy为螺钉挤压模量；Esjy为电源机箱底板挤压模量；Exjy为安装板挤压模量。

螺钉的剪切刚度为柔度的倒数，表示为：

提取模型中电源机箱底板的厚度ts= 8，安装板的厚度tx= 15，带入电源机箱底板、安装板及螺钉的材料参数，得到螺钉简化模型的等效刚度分别为KN=118 700 N/mm,Kτ=6 400 N/mm。

3 有限元仿真应力计算

3.1 有限元模型建立

电源机箱底板与安装板之间的连接螺钉采用钉元进行模拟，每个钉元使用3个一维弹簧单元进行建模，弹簧的刚度来自于螺钉简化模型的等效刚度。在电源机箱底板与安装板配合面的螺钉铰制孔中心各建立独立节点，分别以独立节点为主节点与孔壁上所有的节点创建多点约束，约束3个方向的平动自由度。然后在这两个独立节点之间建立弹簧单元，模拟螺钉的轴向拉压刚度和面内剪切刚度[8]。

按照上述原理及流程，对其他连接进行同样处理，最终得到系统的仿真模型，如图3所示。A、B为电源机箱与载机间的基础约束，基础约束按照6个方向的自由度全部约束进行处理。C为16个集中质量与安装位置的刚性连接。D为连接6个零部件的周围节点的耦合自由度处理。

图3 系统有限元仿真模型

3.2 系统应力仿真

电源机箱作为航电设备，安装在飞机平台上，工作时需要承受三轴半正弦载荷冲击，峰值加速度为150 m/s2，脉冲宽度为11 ms，载荷谱如图4所示。

图4 冲击载荷波形

施加半正弦波载荷，对电源机箱系统（含安装板）进行系统冲击仿真。经结果对比，发现飞机翼展方向受力最为恶劣，得到的该方向下系统的变形与应力云图如图5所示。

图5 翼展方向的变形与应力云图

3.3 螺钉应力提取

系统在冲击下，一方面螺钉会承受轴向拉力；另一方面，在强大的外力作用下，克服静摩擦力后，电源机箱底板与安装板会发生微小滑移，螺钉与孔壁之间产生挤压从而承受横向剪切力。提取最为恶劣的螺钉处多点约束反力[9]，得到螺钉轴向力与剪切力随时间变化情况，如图6所示。

图6 螺钉承力时间历程曲线

4 强度与寿命校核

4.1 强度校核

提取螺钉轴向拉应力和横向剪切应力，按照两个工况分别核算螺钉在冲击载荷下的安全性。根据材料力学理论公式，螺钉的轴向拉应力和横向剪切应力可以表示为：

式中：kσ为力学仿真修正系数；FN为轴向载荷，取冲击工况时间周期内的最大值；Fτ为剪切载荷，取冲击工况时间周期内的最大值；d为螺钉直径[10–11]。

根据图6所示的载荷时间历程曲线，得到FN=3 057.7 N,Fτ= 648.7 N。取kσ= 1.3,d= 8 mm。带入式（4）得到σ实际=79.1 MPa,τ实际=16.8 MPa。

螺钉材料为30CrMnSiA，根据该材料的特性，其许用轴向拉应力与剪切应力可以由其屈服强度σs进行折算获得，于是得到材料的许用轴向拉应力为[σ]= 0.7σs= 716 MPa，材料的许用剪切应力为[τ]= 0.25σs= 256 MPa。由于螺钉承受交变载荷，因而取许用安全系数[S]=3对螺钉强度进行校核：

因此，优化后螺钉满足强度设计要求。

4.2 寿命校核

根据材料力学第四强度理论，螺钉的组合应力可以表示为[12]：

为确保系统安全，遵从保守原则，FN和Fτ取4.1节中的冲击载荷下最大值来计算组合应力。将这些已知条件带入式（5），得到组合应力σ组合=96.6 MPa。

按照疲劳设计理论，疲劳极限与强度极限具有较好的相关性[13]。对于碳钢或合金钢，材料的疲劳极限可以表示为：

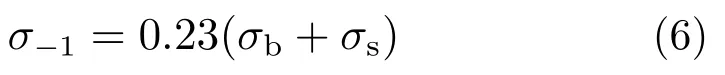
式中：σb为材料抗拉强度；σs为材料屈服强度。带入材料数据，得到螺钉材料30CrMnSiA的疲劳极限σ−1=529 MPa。

考虑螺钉的加工因素及应力集中情况，螺钉可以承受的疲劳极限应力幅值可以修正为[14]：

式中：ε为尺寸偏差系数，取1；kt为螺纹制造加工工艺系数，取1.25；kn为螺纹材料修正系数，取1.25；k′σ为螺纹应力集中系数，取1.5。安全系数[S]取2.5，带入这些参数，得到螺钉的疲劳许用应力值为：

因此，螺钉疲劳寿命满足设计要求。

5 试验验证

为验证仿真计算的可信度，搭建如图7所示的冲击试验环境，用来模拟电源机箱承受的冲击载荷，以获得与仿真计算一致的输入激励，为后续的应力比对提供支撑条件。

图7 振动试验环境

动态应力测试系统采用江苏东华测试技术有限公司生产的DH5920，系统组成如图8所示。

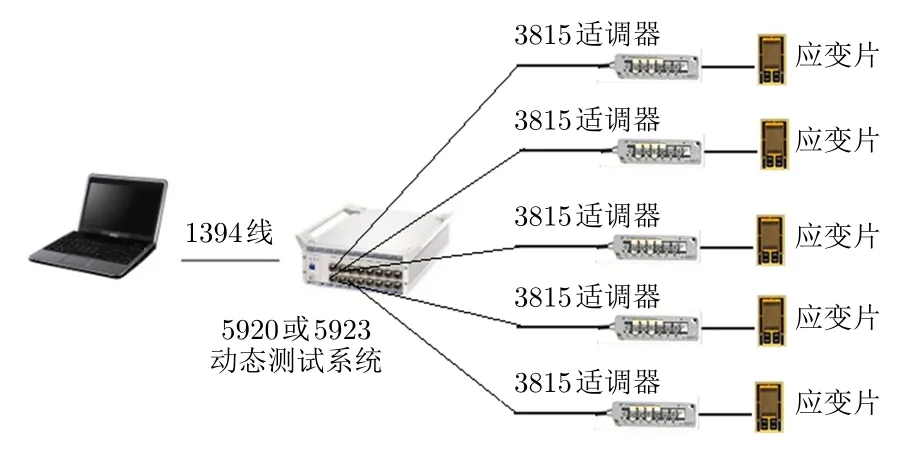
图8 动态测试系统

由于螺钉平直面较小，难以粘贴应变片，因此无法直接测量螺钉的应力水平。为此，将应变片置于图7所示区域，通过对应变片测量的应力值与仿真应力值进行对比，反向佐证螺钉应力仿真计算值符合真实情形。通过测试，得到测试点的应力值如表1所示，其中Mises应力最大值为34.9 MPa。与相同位置（图5（b））的仿真应力进行对比，误差不大于7%，完全满足工程校核精度要求。因此，可以认为附近的螺钉载荷与实际情况基本匹配，螺钉强度与寿命的校核结论可信。

表1 应力测量值 MPa

6 结束语

本文以某电源机箱和安装板连接螺钉为例，详细介绍了系统级产品内部螺钉的载荷获得、应力提取、强度校核、寿命预测及试验验证全流程。相比于传统螺钉强度校核，本文阐述的方法具有以下特点和优势：

1）通过建立螺钉等效刚度模型将螺钉模型简化，带入系统有限元仿真模型，计算效率大大提升。

2）通过系统仿真，较为精确地获取了螺钉的载荷状态，同时也准确地表征了各螺钉点的承载情况，相对于传统的应力不均衡系数，计算精度大大提高。

3）可以跟随系统仿真模型进行快速迭代，适合工程方案阶段快速迭代优化需求，可为同类工程问题提供参考借鉴，并具有一定的应用价值。