基于位移突变准则的颗粒流强度折减法

戴健健， 朱振学， 叶 楠， 苏 超*， 张 恒

(1.河海大学水利水电学院， 南京 210098； 2.吉林省水利水电勘测设计审查总站， 长春 130033； 3.吉林水利科学研究院， 长春 130022)

边坡稳定分析作为岩土工程中重要的研究课题，其评价合理与否直接关系到边坡工程的成败。边坡失稳破坏时往往存在岩土体的滑动、平移与转动等现象，这是一个复杂的过程且在宏观上表现出非连续性。颗粒离散元[1]作为一种典型的非连续介质分析方法，在边坡工程中得到广泛应用，李龙起等[2]采用颗粒流程序PFC(particle flow code)模拟降雨作用下土质边坡的变形特征；戎泽鹏等[3]联合PFC3D和Rockfall对危岩体进行分析；张志飞等[4]使用PFC研究反倾层状岩质边坡的变形及破坏过程；Wu等[5]利用PFC对永嘉山体滑坡的动力过程进行分析。在边坡稳定分析中，强度折减法[6]由于概念明确、容易实现，周健等[7]将其引入到颗粒流中，采用累计位移或不平衡力作为临界破坏准则，为颗粒流用于评价边坡的稳定性提供了新思路。采用颗粒流强度折减法评价边坡稳定性时，能否直观合理地判断边坡处于临界破坏状态显得至关重要。

近年来关于颗粒流强度折减法在边坡稳定性方面的研究较多。王培涛等[8]选取了黄金分割点作为折减比例，采用不平衡力收敛准则对铁矿现场岩质边坡开挖扰动前后的变形特性和稳定性进行了研究。王鑫等[9]以坡顶位置的颗粒作为特征点，通过绘制不同折减系数与特征点x方向位移的关系曲线，以曲线出现明显拐点时的折减系数作为稳定系数，对沿海吹填土堤边坡的稳定性进行了颗粒流模拟。田雷等[10]在边坡顶部设置测量圆，绘制测量圆内颗粒的平均位移与折减系数关系曲线，以曲线位移突变时的折减系数作为稳定系数，分析了植被护坡对边坡稳定性的影响。汪华安等[11]通过绘制坡面测点的最大位移与折减系数关系曲线，采用曲线转折点处的折减系数作为边坡稳定系数。金磊等[12]提出一种基于能量演化的方法来判别边坡是否失稳破坏，当颗粒做功和摩擦耗能超过颗粒接触应变能，且保持一定速率持续增长时则判定为失稳状态，并将该方法用于土石混合边坡稳定性分析中。

上述关于颗粒流强度折减法失稳破坏判据的研究多集中在颗粒不平衡力、位移和颗粒体系能量方面。颗粒不平衡力比值以及位移临界值的选取均具有主观性与经验性，目前尚无统一的标准。采用颗粒位移与折减系数关系曲线求解稳定系数直观明了，但关于特征颗粒位置以及位移的选择有待进一步探究。对位移突变准则进行改进，通过绘制坡面不同位置的特征颗粒位移与折减系数关系曲线求解边坡稳定系数，并与有限元强度折减法和极限平衡分析的结果进行对比，为进一步验证该方法的合理性与可靠性，模拟了滑坡的破坏形态，并从变形和应力特征两个不同角度分析其破坏机理。

1 边坡算例及土体细观参数标定

1.1 边坡算例

图1为某土质边坡工程的断面示意图，土体力学参数如表1所示。

表1 土体力学参数Table 1 Soil mechanical parameters

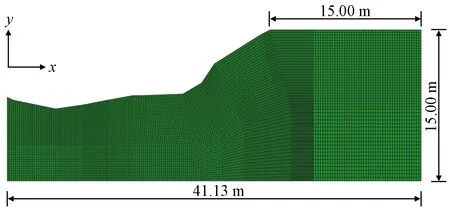
图1 边坡算例断面图Fig.1 Cross-sectional view of slope calculation example

1.2 土体细观参数标定

利用PFC2D程序对土体进行双轴压缩试验标定其细观参数，构建的土体双轴压缩试验的模型尺寸为3.0 m×1.5 m(高×宽)如图2所示。土体颗粒采用接触黏结模型[13]，该模型能真实地反映黏土类黏性材料的宏观力学特性。采用试错法经大量计算最终确定土体的细观参数如表2所示。选取100、200、300 kPa 3个不同的围压，对土体试样进行双轴压缩试验，可得试样的峰值强度分别为206.32、379.12、543.48 kPa。通过MATLAB回归分析可求得土体的凝聚力为15.08 kPa，内摩擦角为14.79°，土体在不同围压下的偏应力-轴向应变曲线如图3所示，其莫尔圆与强度包络线如图4所示。

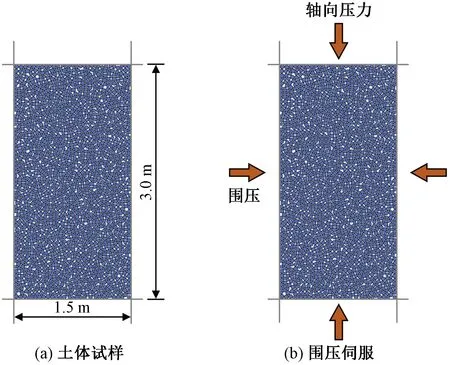
图2 双轴压缩试验模型Fig.2 Biaxial compression test model

图3 偏应力-轴向应变曲线Fig.3 Deviator stress-axial strain curve

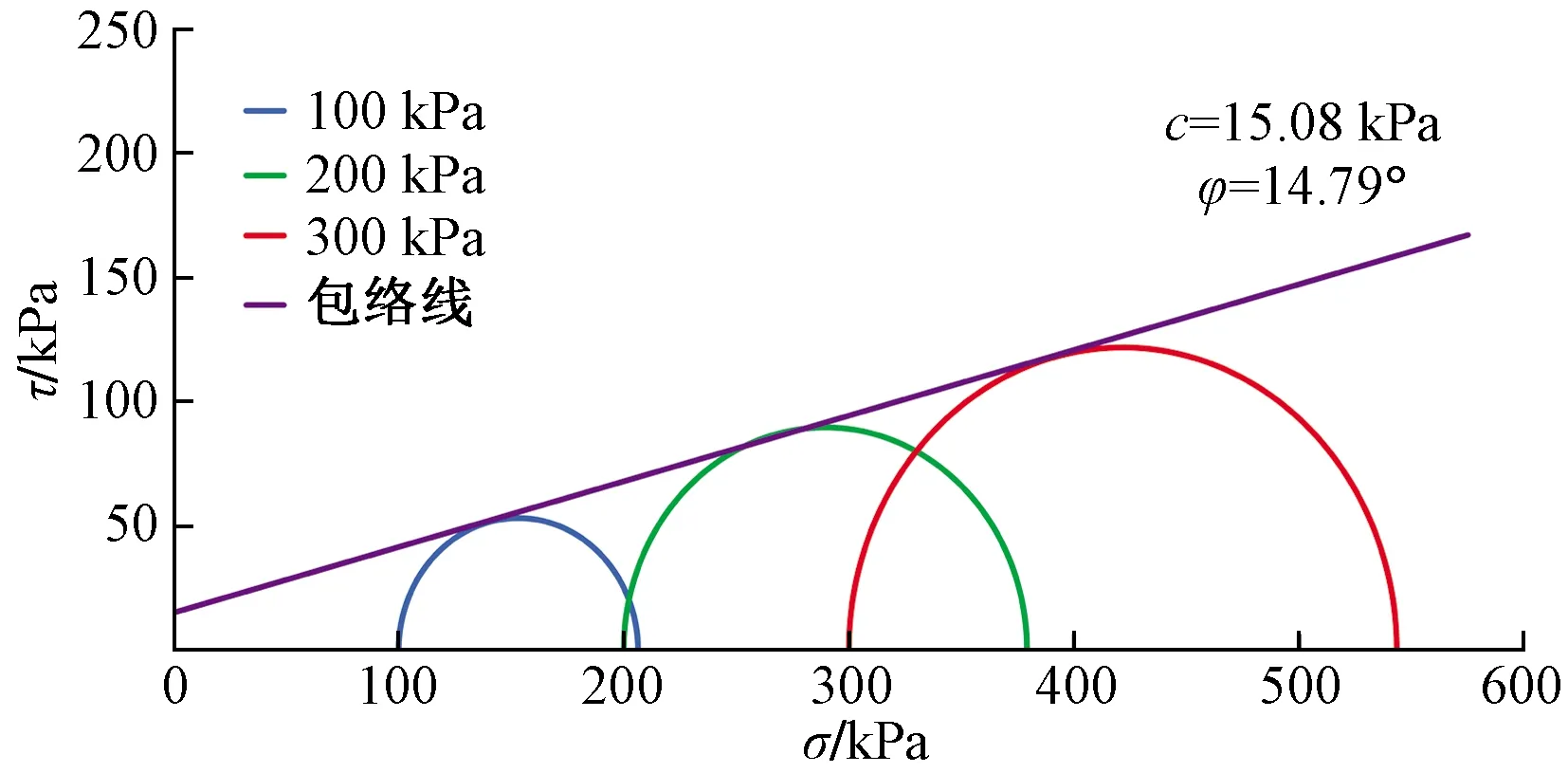
τ为剪应力；σ为正应力；c为凝聚力；φ为内摩擦角图4 莫尔应力圆与强度包络线Fig.4 Mohr’s stress circle and strength envelope

表2 土体颗粒的细观参数Table 2 Micro-parameters of soil particles

2 边坡颗粒流模型构建

根据该边坡工程的断面图，采用PFC2D与AutoCAD相结合的方法建立边坡模型，运用geometry import与wall import geometry命令将dxf格式文件导入生成边坡的轮廓与墙体，运用ball distribute命令生成土体颗粒，在建立颗粒流计算模型的过程中，以颗粒的平均比率小于1.0×10-5时作为平衡条件，在模型达到平衡状态后进行颗粒速度和位移的清零，赋予土体颗粒的细观参数。最终建立的边坡颗粒流模型如图5所示，计算区域取坡顶向右延伸10 m，坡高12 m，颗粒总数为120 888个，两侧和底部采用墙体约束。此外，在边坡内部4个不同位置布设半径为1.0 m的测量圆，以记录坡体在滑动过程中应力的变化情况。

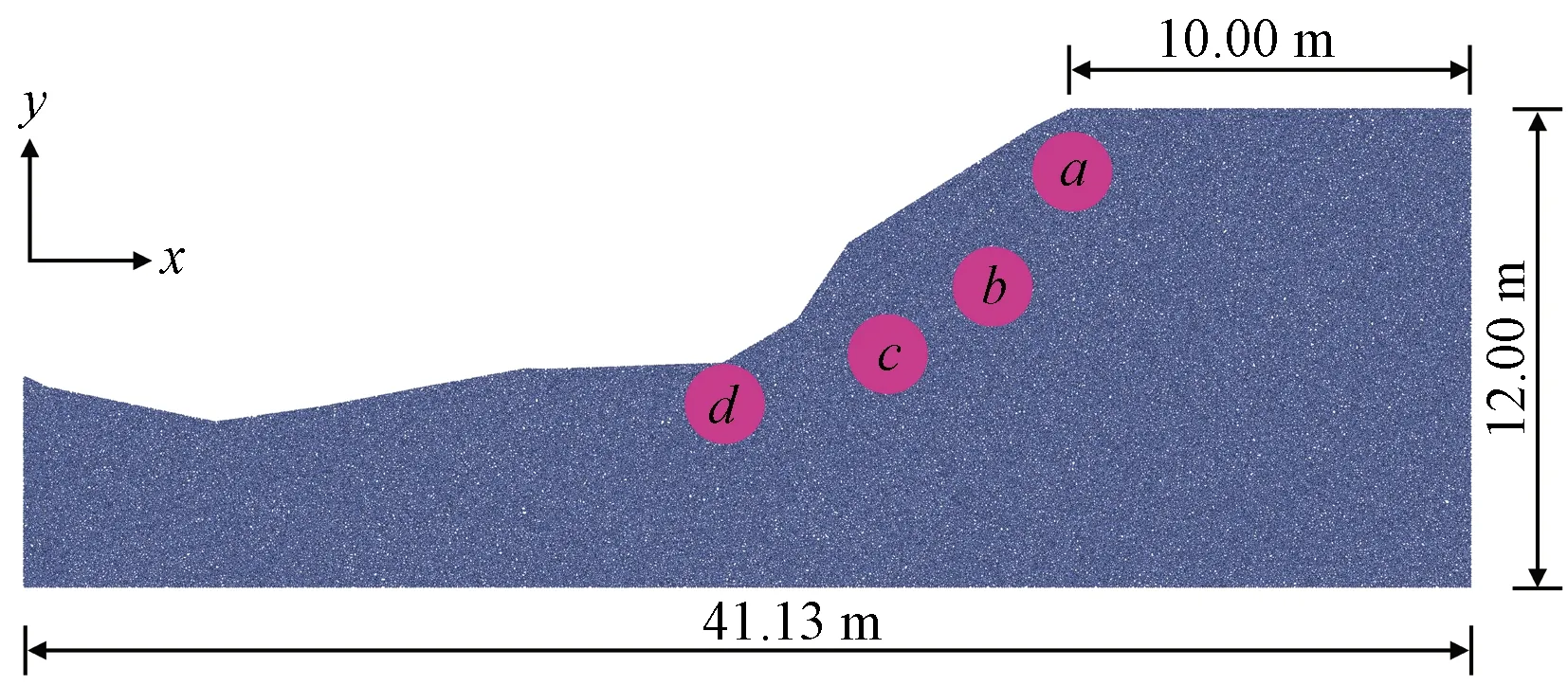
a～d为测量圆图5 边坡颗粒流模型Fig.5 Slope particle flow model

3 颗粒流强度折减法求解边坡稳定系数

颗粒流强度折减法[6]的基本思路为将颗粒的法向、切向黏结强度和摩擦系数同时进行折减，其计算公式为

(1)

式(1)中：Fs为滑坡的稳定系数；cbtenf为颗粒的法向黏结力；cbshef为颗粒的切向黏结力；fric为颗粒间的摩擦系数；cbtenfcr、cbshefcr和friccr分别为颗粒的临界法向黏结力、切向黏结力和摩擦系数。

对于同一边坡而言，不同研究者因选取临界破坏判断准则的不同将得到完全不同的计算结果，这将导致将该方法用于边坡稳定性的评价具有强烈的主观性与经验性。为更加直观、合理地求解边坡稳定系数，同时为减少人为的主观性与经验性，本文通过绘制特征颗粒位移与折减系数关系曲线求解边坡的稳定系数，具体思路为：①对土体颗粒的法向、切向黏结强度和摩擦系数同时进行折减；②选取一系列位于坡面位置的特征颗粒，记录计算完成时特征颗粒位移值；③绘制选取的特征颗粒位移与折减系数关系曲线；④对于每个特征颗粒，其位移有明显突变趋势时有一个对应的折减系数，取所有对应的折减系数的最小值作为边坡的稳定系数。

3.1 特征颗粒的选取

采用位移与折减系数关系曲线求解边坡稳定系数直观明了，在颗粒流中，位移可采用颗粒的位移或测量圆内颗粒的平均位移。由于测量圆的位置是固定的，若在坡顶布设，坡顶会出现明显张拉缝隙，坡体下滑导致测量圆内的颗粒数量在不断变化。测量圆位置布设在滑动面区域最为合适，但滑动面事先是未知的。在边坡发生破坏时，坡面的颗粒随坡体一起滑动，有十分明显的位移变化，因此本文选用坡面位置的颗粒作为特征颗粒。

在滑坡过程中，考虑到坡脚处的颗粒会出现滑移堆积以及坡顶处滑坡体易出现二次破坏(图6)，因此选取坡脚至坡顶中间处6个坡面位置的颗粒作为特征颗粒，选取原则为选用边坡轮廓线处的颗粒以及颗粒的位置分布均匀，特征颗粒的位置如图7所示。

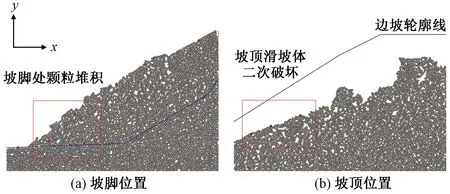
蓝线为边坡的轮廓图6 坡脚和坡顶处特征颗粒Fig.6 Characteristic particles at the toe and top of the slope

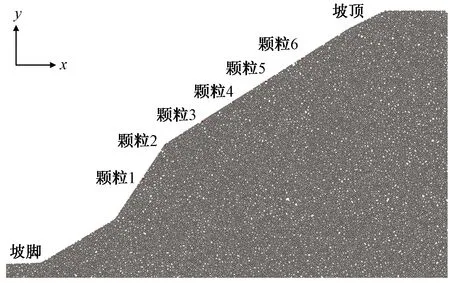
图7 特征颗粒位置示意图Fig.7 Schematic diagram of the location of characteristic particles

3.2 特征颗粒位移与折减系数关系曲线

经大量的滑坡颗粒流计算并综合考虑计算时间成本，最终确定颗粒流强度折减法的计算时步取为5×105步。对边坡施加重力，记录不同折减系数计算完成时特征颗粒的位移值，绘制的坡面位置特征颗粒位移与折减系数关系曲线如图8所示。

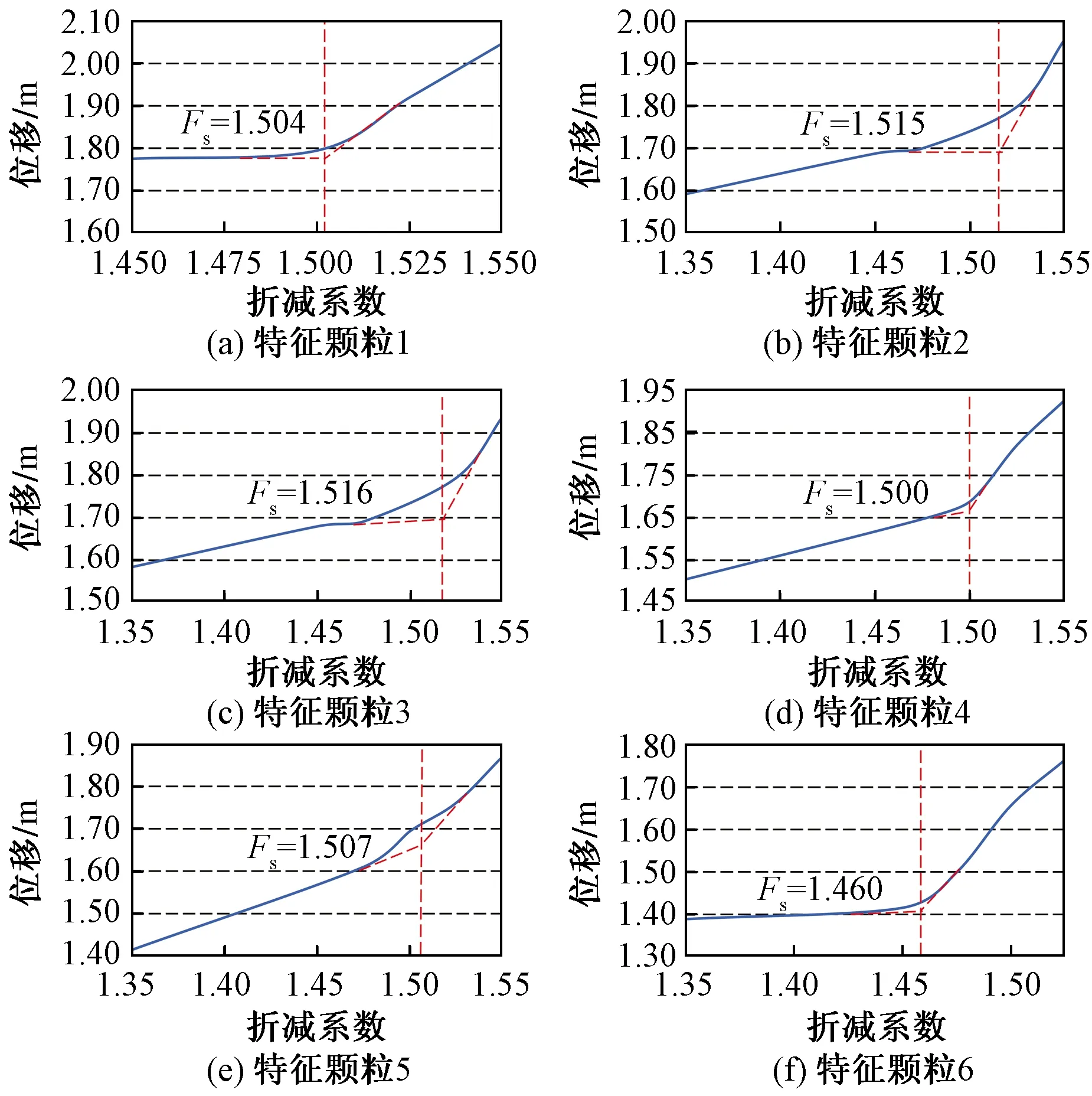
图8 特征颗粒位移与折减系数关系曲线Fig.8 The relationship curve between characteristic particle displacement and reduction coefficient

3.3 边坡稳定系数的求解

对于每个选定的特征颗粒，其位移有明显突变趋势时有一个对应的折减系数。该折减系数的确定方法为：①当曲线有明显拐点时，取拐点对应的折减系数；②当特征颗粒位移与折减系数关系曲线有明显加速趋势段时，通过绘制关系曲线在位移拐点附近的两条切线确定。

根据图8所示的特征颗粒位移与折减系数关系曲线，确定的折减系数如表3所示，从安全的角度出发，确定边坡的稳定系数为1.46。

表3 特征颗粒对应的折减系数Table 3 Reduction factor corresponding to characteristic particles

为进一步探究上述方法求解边坡稳定系数的适用性，首先基于强度折减法采用有限元软件ABAQUS求解边坡的稳定系数。边坡有限元计算模型共有12 700个单元，13 005个结点，采用平面应变单元CPE4，如图1所示。采用位移突变准则求得的稳定系数为1.586，计算不收敛时的塑性区如图9所示。其次对该边坡进行极限平衡分析，采用Bishop法求得的稳定系数为1.612。图10为相应的滑动面位置。采用颗粒流强度折减法求得的稳定系数比有限元强度折减法和Bishop法的更小，这是由于颗粒流作为一种非连续数值方法，通过力-位移关系模拟颗粒间的接触，当法向力或切向力超过允许的强度后，颗粒间的接触黏结可发生断裂导致的。

图9 计算不收敛时的塑性区Fig.9 Plastic zone when calculation doesn’t converge

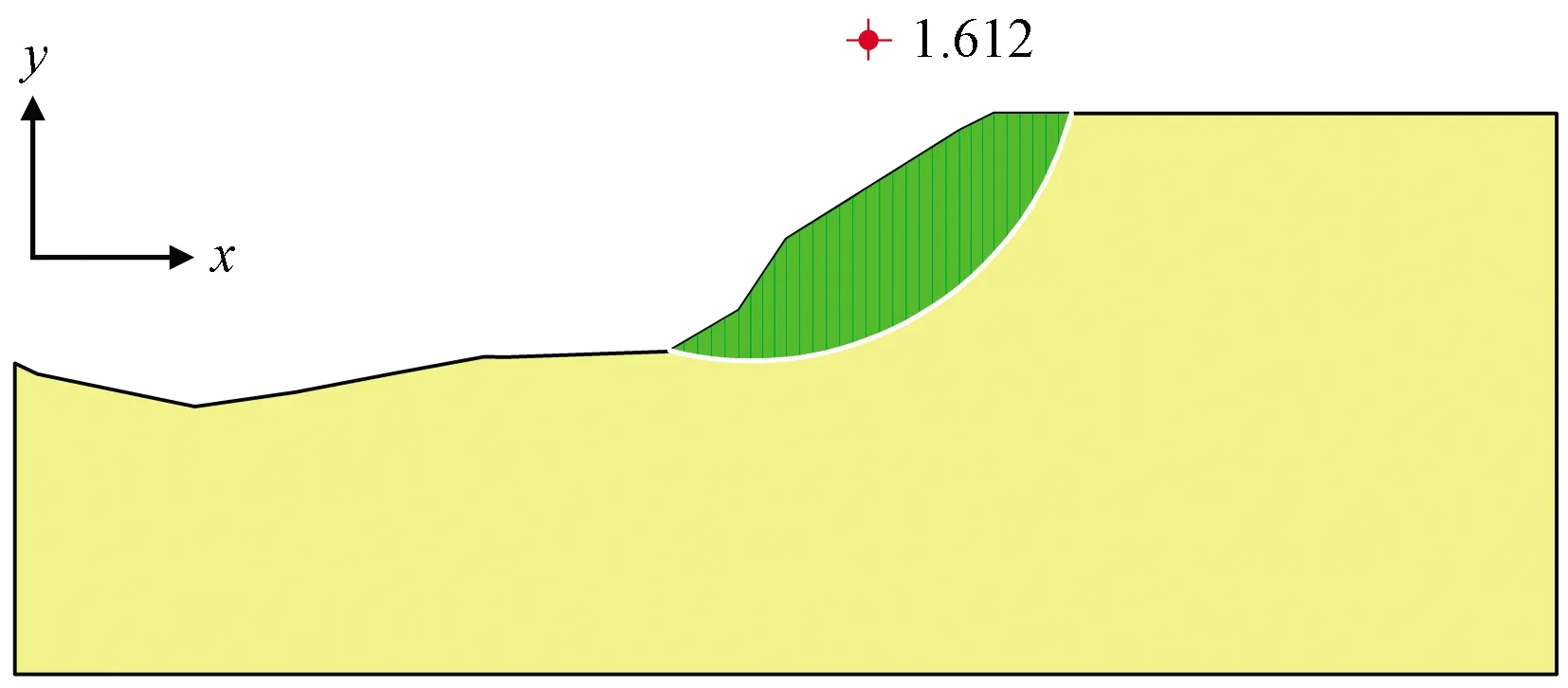
图10 Bishop法滑动面Fig.10 Bishop method sliding surface

采用改进的位移突变准则，通过绘制特征颗粒位移与折减系数关系曲线求得的边坡稳定系数为1.46。对于岩质边坡只需采用可描述岩石力学特征的接触模型，亦可采用上述方法求解其稳定系数；而对于三维边坡，可在不同剖面位置选取坡面不同位置的颗粒作为特征颗粒，采用同样的方法进行求解稳定系数。

4 滑坡破坏过程模拟及其机理分析

4.1 变形特征分析

根据上述方法求得的稳定系数对土体颗粒的法向、切向黏结强度和摩擦系数同时进行折减1.46倍，对边坡施加重力进行破坏形态的模拟，计算时步取1×106步。

由颗粒流数值模拟的结果，在计算初期，坡脚处的土体颗粒变形不断累加，在重力作用下，在5×104步时坡顶向下沉陷，坡脚处颗粒向外挤出，部分颗粒的接触黏结断裂。1×105步时坡脚处发生挤压破坏变形加剧，坡内颗粒接触黏结断裂形态向圆弧形式发展，土体发生剪切破坏。在上覆压力作用下，断裂的接触黏结贯穿坡顶，贯通面形成，坡顶失去支撑的作用，2×105步时坡顶产生明显张拉缝隙，坡体发生失稳破坏，沿贯通的圆弧式断裂黏结滑移[图11(b)]。随着时间的推移，断裂的接触黏结继续发展，破坏的坡体继续下滑，3×105步时滑坡体颗粒间部分黏结破坏，出现二次破坏，由于土体具有一定凝聚力，滑坡体在一些局部位置发生张拉破坏，滑坡体局部破碎，并滑移堆积至坡脚处。5×105步时坡体滑动面与Bishop法求得的滑动面以及有限元强度折减法计算不收敛时的塑性区形态一致[图11(d)]，这表明采用本文方法求解边坡稳定系数的合理性与可靠性。图11(e)为7×105步时滑坡的形态，在1×106步时滑坡体趋于稳定。由模拟的滑坡过程可知，颗粒流强度折减法很好地再现了整个滑坡破坏过程，而有限元强度折减法只能给出塑性区的分布，极限平衡分析如Bishop法只能给出圆弧滑动面的位置。

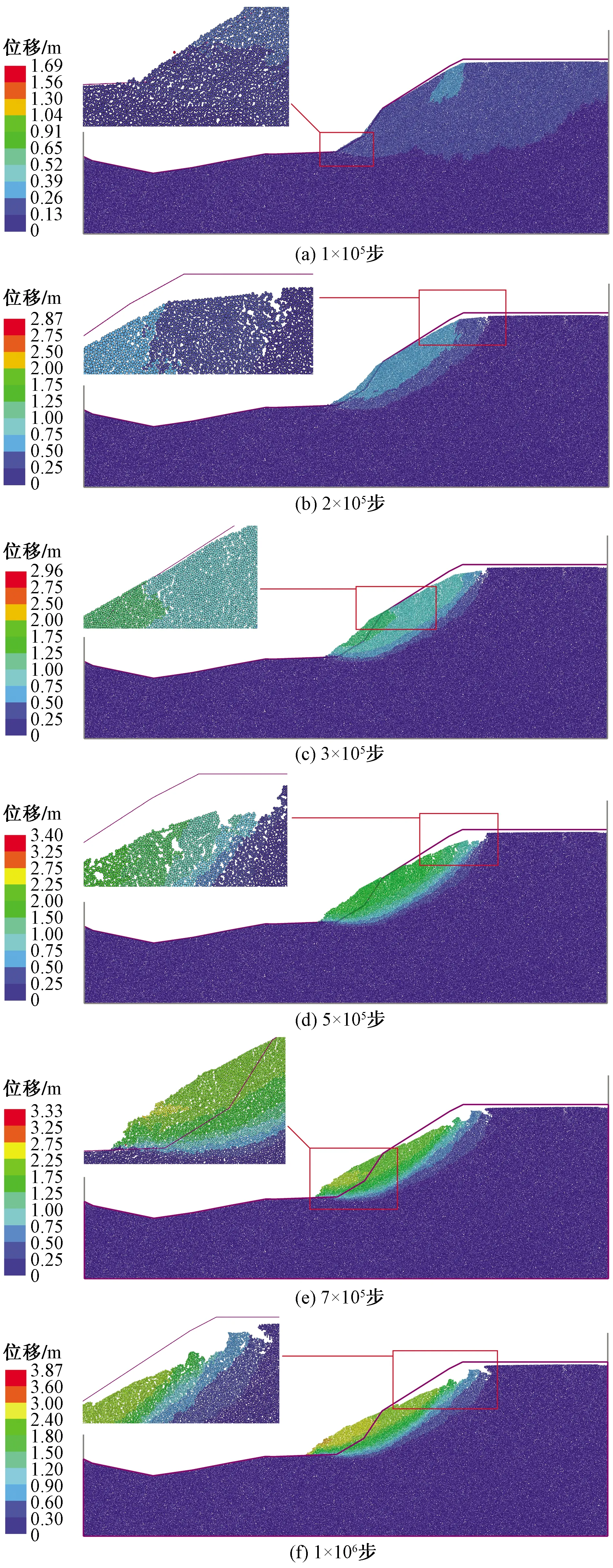
紫色线条为原状边坡的轮廓线图11 边坡滑坡破坏形态Fig.11 Slope landslide failure mode

4.2 应力特征分析

采用上述求得的稳定系数对土体颗粒的细观参数进行折减，对边坡施加重力进行1×106步的计算。该边坡滑坡破坏过程中记录的应力(以拉为正)变化曲线如图12所示，坡顶位置土体颗粒由于接触黏结断裂产生张拉裂缝和滑移，测量圆a内x方向和y方向应力由起初增大的拉应力变成压应力，当坡体下滑时压应力逐渐平缓变化。随着黏结断裂的增加，坡体持续向下滑移，测量圆b内x方向和y方向压应力变化平缓。测量圆c内y方向压应力变化比x方向大，这是由于在重力作用下，断裂的接触黏结贯穿坡顶，随着坡体的滑移，滑坡体颗粒间的部分黏结亦破坏，滑坡体发生张拉破坏和挤推作用所导致的。测量圆d位于坡脚位置，由于坡体下滑时的挤推和堆积作用，使得x方向压应力比y方向更大。

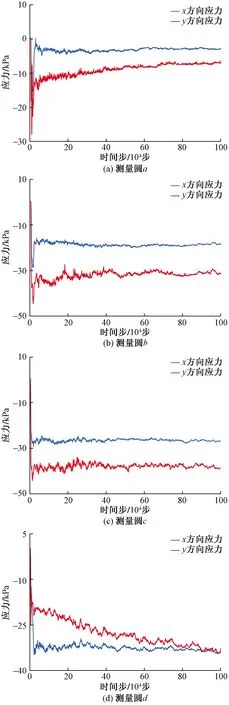
图12 边坡测量圆的应力变化曲线Fig.12 The stress change curve of the slope measurement circle

5 结论

(1)考虑到在滑坡过程中坡脚处颗粒会出现滑移堆积，坡顶处滑坡体易出现二次破坏，建议选取坡脚至坡顶中间处坡面位置的颗粒作为特征颗粒。

(2)采用本文方法对边坡稳定性进行评价时，可模拟颗粒间接触黏结断裂导致土体发生剪切破坏，断裂的黏结逐渐贯穿坡顶，坡体发生失稳破坏，很好地再现了整个滑坡破坏形态，这是有限元强度折减法和极限平衡分析无法模拟的。

(3)本文方法模拟得到的边坡破坏形态与有限元强度折减法和Bishop法的结果一致，验证了该方法的合理性与可靠性。