风力发电厂与电力存储系统联合运营商的最优投标决策研究
孙心玥,刘 健,欧 盟
(南京理工大学 经济管理学院,南京 210094)
近年来,新能源的发展已是大势所趋,可再生能源如水能、风能、太阳能等正在成为许多国家发电的重要组成部分[1].基于风电的良好环境效益以及逐步降低的成本,文献[2]分析了中国风能资源现状的分析,指出风电必将成为中国新能源发电的领跑者.随着中国可再生能源的快速发展,针对新能源发电的补贴政策也在不断完善[3],将进一步促进中国风电产业的发展.考虑到电力市场特殊的运作机制,即主要采用提前投标机制:将电力视作期货[4],在企业之间进行交易,各电力企业与市场之间按照投标、竞标、实时操作的顺序来进行电力交易[5].电力作为商品,与普通商品的不同之处在于:电力作为社会稳定发展的保障,其供给和需求必须保证实时匹配[6],这也为电力企业的经营带来了难度.由于风力发电极大依赖自然环境,其发电量存在极大的不稳定性,准确预测风力发电未来供给的电量十分困难.因此当联合运营商参与日前电力市场投标竞争时,如何处理其日前投标量与当日实际发电量的偏差显得尤为重要.而在电力市场,管理者为维持市场稳定,将采取惩罚机制:当实际发电量与投标量出现偏差时,市场管理者将对其进行惩罚[7].由于风力发电的随机性,运营商在参与市场投标时可能会面临惩罚风险,影响其收益,如:作为供应方,若其实际发电量未达到投标量,出现电力短缺,则需要从市场上以高于当前电价的价格额外购买电力弥补,这部分购买支出即为惩罚金;若供应方向市场提供了超过投标量的电能,出现电力盈余,也需要支付一定的费用消耗多余的电能[8].在电力市场中,对每个参与竞标的电力供应商而言,理想策略是最大化自身利润[9],因此基于风力发电的不可预测性,设置科学合理的投标决策以及投标量十分重要.
针对风力发电的不可预测性和不确定性,为满足电力市场供需实时匹配的要求,有效的策略是与电力存储系统相结合[10].电力存储系统的作用其一是平滑电力供给波动[11],在电量不足以满足市场需求时,通过存储系统放电来满足剩余需求,而在电量超过市场需求时,将多余电量存入系统备用.电力存储系统的作用其二是延后电力的售出,电力运营商会对未来电价进行预估,准确的短期电价预测对于供应商竞价策略的制定至关重要[12].当预测未来电价更高的情况下,当前阶段不出售电力亦或从市场买入额外电量存入系统中,在未来高价时再卖出,从而获得更高的利润[13].总之,电力存储系统的使用,有助于提高电能的利用率,减少惩罚金的支出,增加收益.文中通过报童模型对风电发电厂和电力存储系统的联合优化投标机制问题进行研究.
现有的电力存储系统主要有抽水蓄能系统以及电池存储系统,现有的研究主要集中在利用不同方法对当前组合发电进行调度优化从而实现收益最大.对于抽水蓄能系统,为将日常运营成本降至最低,文献[14]研究如何结合使用风力发电机和抽水蓄能来满足市场电力需求,抽水蓄能系统的原则在于当市场电力需求低、电价低时从市场买电进行抽水,在电力需求高、电价高时放水发电售出获得利润[15].对于电池存储系统,文献[16]采用顺序随机决策过程,制定了联合电池存储的风电场控制方案.针对电池储能的动态能量特性,文献[17]以锂电池储能为例,提出了一种基于能量分配的锂电池储能电力市场投标策略.为实现微电网系统经济和环境双重目标的优化运行,文献[18]提出一种经济与环保协调控制下的微电网优化调度模型.
关于电力投标,多数研究集中在发电厂商的竞价策略上,包括不完全信息下利用贝叶斯博弈模型研究发电商的竞价策略[19];利用人工神经网络预测其他电力供应商的投标行为,并在评估风险后,给出电力供应商在利润最大化下的竞标电价[20];采用两阶段优化法,考虑风电出力和电力现货市场价格的不确定性,解决风储电站参与电力现货市场竞价与运行计划问题[21]等.不同于竞价策略的研究,文中针对电力投标主要通过报童模型研究投标决策及其投标量的问题.
传统的报童问题主要是面对市场中需求的不确定性,如何对产品的订购和库存做最优决策,如:利用贝叶斯预测更新的报童模型给出企业最优库存策略[22];在供应商回收零售商卖剩的产品并在此后再次出售的背景下,利用报童模型研究最优订购量[23]等.文中基于风力发电供方的不确定性和不可预测性,而需求方确定的情形,利用报童模型对风力发电商的最优提前投标决策以及投标量进行研究.与传统经典报童模型的不同之处在于,文中主要考虑供方的不确定性[24].
针对具有特殊性的电力商品,在考虑需求方确定而供给方不确定性的情形下,文中首先通过报童模型,以风力发电厂和电力存储系统联合优化进行投标决策为背景,基于卖出和买入电力的不同投标,将运营商的投标决策具体分为3种情况,分别建立利润模型并进行优化求解,从而得到最优联合投标量;接着分别对相关参数进行性质分析,得到不同情形下最优联合投标量与市场的惩罚机制,电力的传输效率,储能系统的充放电效率以及政府的补贴额之间的关系;最后,基于分析结果对联合运营商提出管理启示.
1 情形分类及符号说明
对电力市场而言,为了简化求解过程,假设联合运营商仅考虑两个时间段的优化,并假设其投标时对某个时刻电的售价预测为p,同时预测该时刻结束后电的价值为γ,线路传输效率为η.假设电力存储系统,其充电效率为α,放电效率为β,在发电厂和电力存储系统联合优化的背景下,为实现利润最大化,基于未来电价的情形,对投标决策进行分类:
(1) 当γαβ≤p,即运营商将当期产生的电力进行出售所获得的利润大于存入系统留于后期售卖所获得的利润时,其投标决策为向市场出售电力,即卖电.同时,考虑到电力市场中的惩罚金,当实际发电量不足以满足投标量从而造成偏差时,假设其电力短缺的惩罚系数为k(k>1),即需要按高于市场电价的价格对缺少的电量进行额外购买以达到真实投标电量;当投标量小于实际发电量且多余电量已无法被电力存储系统容纳,造成电力浪费时,其电力盈余的惩罚系数为l(不失一般性,0 在当天投标时,根据比较预测时刻的电价与后某个时刻的电价之间的大小关系,存在3种不同情形.在风力发电厂和电力存储系统联合优化背景下,将XJ1作为运营商提前优化时刻的联合投标额,i=1,2,3,即根据3种不同情形所对应的联合投标额,其中:XJ1>0表示卖电,XJ1<0则表示买电.相应地,假设运营商的发电成本为c,实际发电量为y,风力发电的概率密度函数为f(y),遵循Kim和Powell以及Densing的假设及数值实验结论:假设风力发电厂的风力输出为均匀分布[1, 25-26],即y服从均匀分布: (1) 式中:Gmax为风力发电机组发电量上限(由机组的物理条件约束),0为下限. 对于风力发电厂与电力存储系统联合运营商,需考虑其在运作过程中的自身属性,假设初始状态时电力存储系统现有的电量E,当前系统内所存储电能的单位成本m,电力存储系统的容量上限为Cmax.基于当前国家对新能源发电的补贴政策,文中假设运营商在卖电情形下,对其出售到市场上的实际电量进行补贴[27],即运营商通过卖电可获得单位补贴成本s,但若运营商选择买电,进行存储作为后期再卖电获取利润的情形,不设置补贴. 当γαβ≤p,即风力发电厂和电力存储系统联合运营商选择将当期电力存入系统留于后期售卖所获得的利润小于当期售出所获得的利润时,运营商将直接向市场投标计划售出电量,当期所产生及所存储的电量当期卖出. kp(XJ1-Eβη-yη)+s(yη+ Eβη)]f(y)dy (2) (3) (4) (5) 因此,运营商的总期望利润函数为: E1(∏)=∏1+∏2+∏3+∏4= (6) 运营商的目标是期望利润最大化,对式(6)进行优化求解(即求一阶偏导),可得: (7) 此时式(6)二阶偏导为: (8) (9) 则最优投标量为: (10) 结果表明,在利润最大化的目标下,最优联合投标量与电力的线路传输效率,惩罚系数,政府单位补贴额以及电力存储系统的属性都有关.因此,对式(10)中各个参数进行性质分析,可得: (11) 通过式(11)可得下面的性质. 性质1:最优投标量XJ1*随电力短缺惩罚价格系数k单调递减.当k增大时,运营商会因为短缺而支付更多惩罚金,所以会减小投标,来保证按照市场要求的投标量提供电量,减小违约概率,维持电力系统的稳定;当k减小时,投标量会增大,运营商会因为短缺而支付较少惩罚金,所以会增大投标,尽量多地争取市场份额,以期通过出售更多的电力获取更大的收益. 最优投标量XJ1*随电力盈余惩罚价格系数l单调递增.当l增大时,运营商会为实际发出的盈余电力支付更多惩罚金,因此会增大投标量,来减小第二天可能出现的电力盈余;当l减小时,运营商会保守估计自己第二天的实时发电量从而提供较小的投标量,尽量保证能按额交付. 最优投标量XJ1*随线路传输效率η单调递增.当η增大时,线路传输效率提高,运营商同样的发电量可以售出更多电力到市场中,反之当η减小时,在相同的发电量预测下,运营商的投标会减少.与此同时,最优投标量XJ1*与政府提供的单位补贴s呈正相关.当s增大时,补贴量提高,运营商的投标也会增加;反之当s减小时,运营商的投标也会减少. 因此,运营商需要根据以上参数对利润的影响,从而对投标量进行调整. mE+pXJ2]f(y)dy (12) (13) (14) 因此,运营商的总利润函数为: E2(∏)=∏1+∏2+∏3= (15) 对式(15)进行优化分析,可得其最优解为: (16) 在运营商选择从电力市场选择购买电力进行存储用于未来出售时,联合系统的最优买电投标量同样与电力的线路传输效率、电力存储系统的充电效率以及两个惩罚系数都有关.对式(16)进行分析可得: (17) 从而可得下面的性质. 性质2:与性质1的不同之处在于,最优投标量XJ2*随电力短缺惩罚价格系数k单调递增.当k增大时,运营商会因为没有按额完成购买订单而支付更多的惩罚金,由于此时运营商的最优决策是买电,即XJ2*<0,最优投标购买量XJ2*增大即运营商将减小投标购买量.相反,当k减小时,运营商会增大买电的投标购,以确定能充满电力存储系统.与性质1的相似之处在于,最优投标量XJ2*随线路传输效率η单调增.当η增大时,传输效率提高,运营商预估购入存储同样多的电量时,所需要购买的电量减少,即XJ2*增大;反之同理. (18) 其余两种情况的收益函数与式(12,13)类似,可得联合运营商的总利润函数为: E3(∏)=∏1+∏2+∏3= (19) 对式(19)进行优化求解,可得风力发电厂与电力存储系统联合运营商的最优解: (20) 类似的,在利润收益最大化的目标下,联合系统的最优买电投标量与电力的线路传输效率、电力存储系统的充电效率以及两个惩罚系数都有关.同样地,对式(20)进行分析,可得: (21) 从而可得下面的性质. 性质3:与性质2类似之处在于最优投标量XJ3*随惩罚价格系数k单调递增,随线路传输效率η单调增,与性质2的不同之处在于,最优投标量XJ3*与电力盈余惩罚价格系数l也有关.该性质与性质1的不同之处在于XJ3*随惩罚价格系数l单调减.当l增大时,运营商会因为额外向市场购买电力支付更多惩罚金,由于投标决策未买电,即XJ3*<0,所以XJ3*减小即表示运营商会增大投标购 买量,来尽量减小需要额外购买电力的概率;而当l减小时,运营商会减小投标购电量. 对上述3种情形分别进行优化求解,可知未来电价的预测起到非常重要的作用,将情形划分为3类不同的情形,基于第二个周期电价γ在未来时刻的不同预测值,假设电价在3种情形发生的概率分别为:ω1,ω2,ω3(不针对电价的预测方法进行研究),可得利润函数为: E(∏)=ω1E1(∏)+ω2E2(∏)+ω3E3(∏) (22) (23) 根据式(10,16和20),式(23)可表示为: XJ*=ω1XJ1*+ω2XJ2*+ω3XJ3* (24) 对最优解进行性质分析,可得下面的性质. 综上得出管理启示:由于风力发电的间歇性和不可预测性,发电厂与电力存储系统联合运营的情况下,根据对未来电价的预测,运营商主要有两种投标决策:卖电或买电,具体对应3种情形.运营商决定投标售出电量还是购买电量的前提是基于为未来电价的准确预测能力. 当联合运营商决定卖电时,在对联合投标量做出决策时,需要针对相关参数,如市场的惩罚系数,政府的单位补贴额对投标量进行调整:若电力短缺惩罚价格系数k增大,则应适当减少最优投标量,而电力盈余惩罚价格系数l增大时,应适当增加最优投标量;当政府的单位补贴额提高时,也应适当增加最优投标量.当联合运营商决定买电,在对联合投标量做出决策时,同样需要针对相关参数的变化对投标量进行调整:在无额外买电的情况下,当惩罚价格系数k增大时,应适当减小投标购买量,在此情况下,最优投标量与电力盈余惩罚价格系数l无关;在有额外买电的情况下,当k增大时,应适当减小投标购买量;当惩罚价格系数l增大时,应增加投标购买量.而在随机情形时,最优投标量还与对3种情形预测概率的大小关系有关. 联合运营商还应提高电力的线路传输效率,降低损耗成本,关于电力存储设备,也应注重存储系统的充放电效率对利润的影响,应当寻找方法提高充放电效率,降低充放电损耗,增大电量利用率. 文中从可再生能源发电——风力发电企业的视角,结合可再生能源发电的不确定性和难以预测的特点,为实现利润最大化的目标,研究了风力发电厂与电力存储系统联合运营商进行优化策略及相应的提前投标机制和投标量. 通过电力存储系统来平滑风力发电的供给波动,在当日投标时,通过对第二天(下一个优化周期)的市场电价预测值和优化周期结束后市场电价预测值进行大小关系比较,决定其投标决策是售出电量还是购入电量.得出结论如下: (1) 在卖电情况下,最优投标量与不能按额完成订单的惩罚价格系数呈负相关,与对市场有额外需求的惩罚价格系数、线路传输效率以及单位补贴额呈正相关. (2) 在买电且无额外购电需求下,最优投标量与不能按额完成订单的惩罚价格系数和线路传输效率呈正相关.在买电且有额外购电需求情况下,最优投标量与对市场有额外需求的惩罚价格系数呈负相关. (3) 风力发电厂和电力存储联合运营商应当根据未来电价对当期投标量做出决策,针对不同情况,根据不同参数的变化,对投标量进行及时调整,以期使得运营商利润最大化.此外,在应用储能技术时,必须根据电力生产结构、用电规划等的不同,合理应用储能技术,才能够充分发挥储能技术的优势,以实现智能电网经济价值的最大化. 文中利用报童模型对电力发电厂与电力存储联合运营商两阶段的联合投标问题进行研究,但未考虑电力存储的多阶段优化问题,未来将拓展到多阶段,利用多阶段报童模型或动态规划方法来进一步分析.在实际情况下,电力市场中可能会出现负价情况,电力负价的出现将影响电力运营商的存储策略,为此将拓展到电价为负价的情形进行优化求解.文中运营商只向市场提交计划售出量或计划购入量,未来将对同时提交投标量和价格的组合策略进行研究.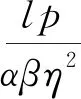
2 联合投标卖电时的模型构建及求解分析
2.1 模型构建
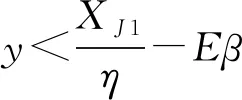
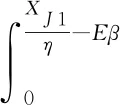
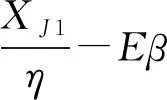
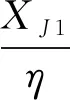

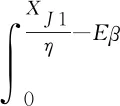
2.2 优化求解与性质分析
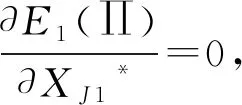
3 买电情况下无额外买电需求时的模型构建及求解分析
3.1 模型建立
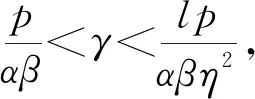
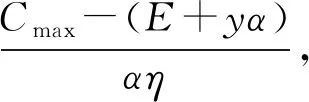
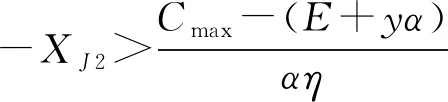
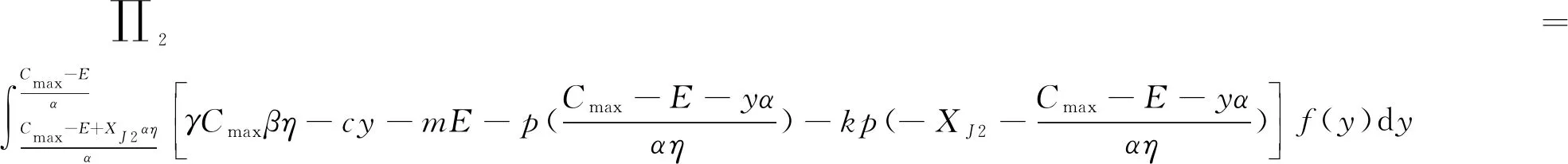
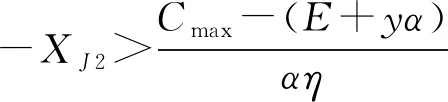
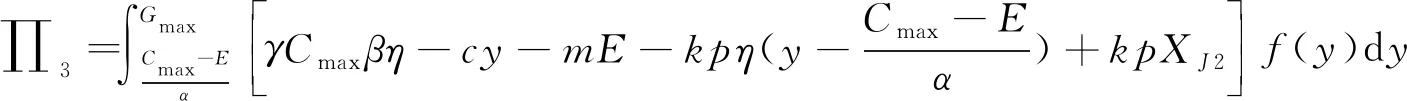
3.2 优化求解与性质分析
4 买电情况下有额外买电需求时的模型构建及求解分析
4.1 模型建立
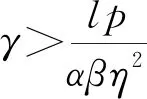
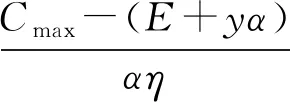
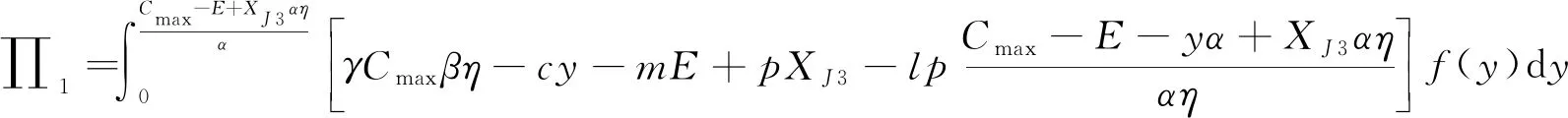

4.2 模型求解与性质分析
5 随机情形下的模型构建及求解分析
5.1 模型建立
5.2 优化求解与性质分析
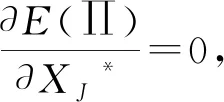
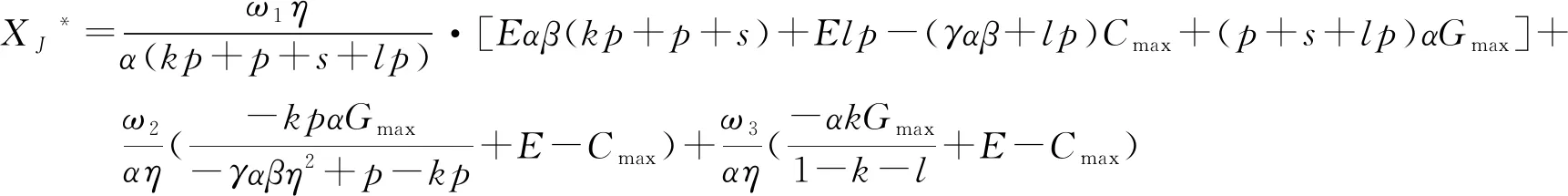
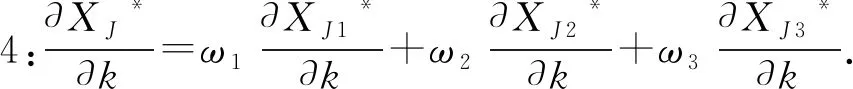
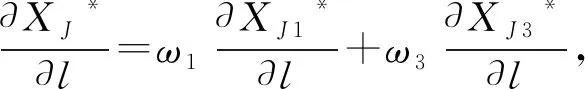
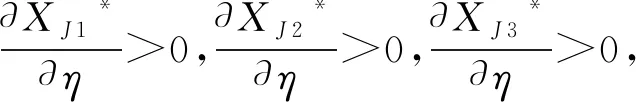
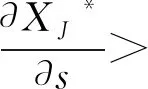
6 结论

