基于Elmer/Ice对玛丽伯德地西部区域的冰盖数值模拟

杨树瑚 徐佳鑫 许德锐 韩彦岭 张云 洪中华

(上海海洋大学信息学院,上海 201306)

提要 西南极冰盖对全球气候变化和海平面升高有着重要的影响,其动力学和热力学过程是极地研究的重点之一。冰盖数值模式的模拟可以在缺乏观测数据的情况下获得研究区域的动力学和热力学过程,已经成为研究南极的一种重要手段。西南极玛丽伯德地靠近福特山脉和罗斯冰架,本文使用Elmer/Ice 模拟了玛丽伯德地西部区域的冰流速场、温度场和应力场。研究发现,该区域冰盖底部温度场变化较小,大部分都达到了压力融点,只有小部分区域的冰盖底部仍处于压力融点以下。使用三个不同的地热通量(80 mW·m-2,100 mW·m-2,120 mW·m-2)模拟得到的底部温度场无明显差异。冰盖表面流速较快,冰盖表面的冰总体上从地势较高的区域流向地势较低的区域,垂直方向对表面冰流速影响最大; 冰盖底部应力场的大小大致和冰厚的变化相反。通过高程剖面图简要分析了冰流速和冰盖应力场的变化原因,认为冰下深谷的存在可能对冰盖流速场和应力场有很大的影响。

0 引言

地球的冰冻圈可分为陆地冰冻圈(包括山地冰川、极地冰盖、冻土、河冰和积雪等)、海洋冰冻圈(包括海冰、冰架等)和大气冰冻圈(冰晶、雪花等)[1],其中极地冰盖在全球气候系统中扮演着重要的角色[2]。极地冰盖存在于南北两极地区,主要由南极冰盖和格陵兰冰盖组成。南极冰盖又可分为东南极冰盖和西南极冰盖。ICESat 在西南极冰盖进行了大量的观测,显示西南极冰盖和南极半岛的冰盖正在变薄[3]。南极冰盖物质平衡的最新研究表明[4-5],西南极洲表现出两种物质平衡变化模式: 西部在增厚,而北面在更快地减薄。西南极冰盖总体正在减薄,其物质损失的速率足以使海平面每年上升近0.2 mm。研究西南极冰盖内部的速度场、温度场以及应力场对研究整个南极冰盖的历史演化及未来发展都有着十分重要的意义。

目前研究南极冰盖的主要手段包括遥感、地面测量以及数值计算[6-7]。遥感技术可以获得大范围的冰盖表面信息,但其穿透能力比较差,很难获得冰盖内部的信息; 地面测量可以获得冰盖内部的信息,但是很难获得大范围数据而且还要耗费大量的人力和时间; 冰盖数值模式可以利用有限的观测数据对冰盖进行大尺度、长时间的研究,获得冰盖内部的速度场、温度场、应力场等冰盖热力学和动力学过程的信息,这使得冰盖数值模式成为研究和预测冰盖演化的有效手段[8]。

冰盖数值模拟是通过数值计算的方法来模拟冰盖的演化以及动力学过程的技术,通过设置一定的初始条件和边界条件,根据实际观测与气候记录给出一系列合适的约束条件(冰盖底部融化冻结状态,冰盖表面温度,冰盖积累率等)来模拟冰盖的动力学状态及其演化过程。通过冰盖模拟技术,可以得到冰盖演化中的一系列参数(冰盖内部温度场、冰流速场、应力场等),是目前研究南极冰盖一种较为有效的方式[7]。区分不同数值模式的通常办法是比较它们处理水平空间的方式,粗略地分类为一维冰流流线模式(一维水平加竖直方向)和二维平面模式(二维水平加竖直方向)[8]。其中流线模式不足之处在于它不能解决冰流方向以及冰流图像在时间和空间上的变化。利用二维平面模式直接积分的垂向过程可以用来处理垂向过程的温度场、应力场、速度场等分布问题。由于这种平面模式涉及对垂向的积分过程,它通常也被称为三维冰盖模式[9]。目前有PISM、SICOPOLIS、Elmer/Ice 等多个冰盖模型应用于格陵兰和南极冰盖的模拟[10]。PISM 基于浅冰近似(SIA)/浅冰架近似(SAA)假设,适用于大尺度冰盖的模拟; SICOPLIS 基于浅冰近似,往往也适用于大尺度冰盖的研究。Elmer/Ice 冰盖模式是一个建立在Elmer 流体力学模式基础上的三维有限元冰盖模式,由芬兰CSC—IT Center for Science(CSC)开发。Elmer/Ice 求解各向同性和各向异性冰流变学的全Stokes 方程,并包含各种基本的摩擦定律[11]。通过Elmer 的多物理方法,还可以解决耦合问题,例如热机械耦合。Elmer/Ice 可以对研究区域使用三角网格进行划分,相对于有限差分模型的矩形网格,能够更好地适应小范围复杂地形区域的模拟。对于大尺度冰盖模拟而言,Stokes 模拟计算量太大,而且冰盖边缘地形复杂,Stokes 模拟求解收敛比较困难,所以目前Stokes 很少用于大尺度冰盖的模拟。

Elmer/Ice 冰盖数值模式最初是由Gagliardini等[12]研究极地冰盖时候提出,后由Zwinger 等[13]在此基础上不断添加新的适合极地冰盖的求解器和用户函数,开发出了支持并行运算的版本,极大地改善了有限元模式计算耗费时间的问题。Gagliardini 等[14]利用Elmer/Ice 冰盖模型,通过设置桩点(Stake)得到Tête Rousse 冰川的空洞数据,模拟了冰盖底部存在空洞和不存在空洞情况下的基底滑动情况,发现冰盖底部的融化会影响冰盖的基底滑移速率。Seddik 等[15]利用Elmer/Ice 模拟了格陵兰冰盖未来一百年的变化情况,并将结果与浅冰假设模式SICPOLIIS 进行对比,发现Elmer/Ice 模式相比于浅冰假设近似模式对于底部滑动的响应更加敏感,作者认为在这一百年内格陵兰冰盖将会使全球海平面上升约15 cm,这与SICPOLIS 的模拟结果12 cm 较为接近。孙波等[16]利用Elmer/Ice 模拟了Dome A 地区的温度和冰龄,发现在Dome A 区域底部冰龄在很大程度上受冰盖厚度和底部融化的影响,其模拟结果为寻找南极最古老的冰提供了很好的理论基础。Fürst 等[17]利用Elmer/Ice 模拟了整个南极冰盖的冰下地形与动力学特征,评估了冰盖内部冰流上升对南极冰流速的影响。Brædstrup 等[18]使用Elmer/Ice 和iSOSIA 模式判断alpine 冰川的基础剪切应力,两种模型在测试条件下产生的应力和滑动模式基本相似。张良甫等[8]利用Elmer/Ice 模拟了南极Gamburtsev 山脉Lambert 冰流区域的温度场和速度场,发现该区域冰盖底部的温度大部分都达到了压力融点,只有少部分靠近内陆的冰盖底部还没有达到; 靠近内陆的区域冰流速度接近于零,而在远离内陆区域冰流速度有了明显增大。由此可见,Elmer/Ice 已经被应用于冰川动力学的多方面研究中,并且推动了对南极冰盖的进一步研究。

1 Elmer/Ice 冰盖模型

1.1 冰盖动力学介绍

冰盖的动力学特征较为复杂,图1 显示了附着浮冰架的地面冰盖的经典几何形状以及它与大气(降雪、融化)、岩石圈(地热通量,地壳均衡)和海洋(融化、崩裂)的相互作用。

图1 是笛卡尔坐标系下冰盖体系的剖面示意图,其中x和y轴在水平面上,z轴垂直向上为正。函数z=h(x,y,t)表示上表面(冰—大气界面)高程的时空分布; 函数z=b(x,y,t)表示冰盖基底高程的时空分布; 函数z=zl(x,y,t)表示岩石圈表面高程的时空分布。对于地面冰盖,冰盖基底和岩石圈表面共同下降(b=zl)形成冰岩界面;z=zsl(t)表示平均海平面高度的时间变化,指出了冰盖与大 气、岩石圈和海洋的相互作用。冰盖上表面的持续降雪被不断压实使冰盖增厚,是冰盖的主要物质来源。冰盖下表面与岩石圈接触,受到地热的影响,冰盖底部可能发生融化,造成物质流失。另一方面,由于冰下山峰或者峡谷影响,冰盖将在重力的驱动下缓慢流动,形成冰流。一般来说,冰盖最高处(冰穹)的冰流基本是垂直向下,而两侧的冰流方向不断向水平方向过渡[19]。因此,冰流将导致冰盖逐渐变薄并且在水平方向上不断延伸。最后,水平延伸的冰盖会在边缘处融入海洋形成冰架并最终崩解为海冰漂浮在海洋上。

图1 笛卡尔坐标系下冰盖(附冰架)体系剖面图 Fig.1.Ice sheet geometry (with attached ice shelf)

1.2 冰盖Stokes 流体方程

冰川动力学认为冰川为不可压缩流体。将v(x,y,z,t)定义为冰盖内部一点(x,y,z)在t时刻的速度场,那么冰的物质平衡方程可以表示为:

结合连续物质的动量守恒定律得到[20]:

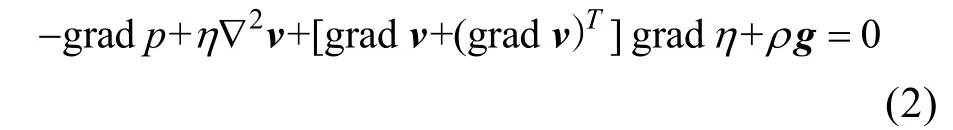
其中,p是冰盖内部应力场,η是黏性系数,g是竖直向下的重力场。该方程被称为Stokes 方程,而符合Stokes 方程的冰流被称为Stokes 冰流[21]。Stokes 冰流的特征是流速较慢并且黏度极大。现代冰川学认为冰是一种Glen 流体,其黏度由温度T和有效应力σe共同决定,如下式表示:

其中,A(T)为比例因子,由公式(4)的阿伦尼乌斯定律(Arrhenius law)导出。当T≤263.15 K 时,A0= 3.9845×10-13s-1·Pa-3,Q=60 kJ·mol-1。当T＞263.15 K时,A0=1.916×103s-1·Pa-3,Q=139 kJ·mol-1。

从公式(2)和(3)可以看出,冰川动力学的场方程(1)包含了随温度变化的粘度η,因此场方程(1)变成了一个热动力学耦合问题。为对其求解,需要获得冰盖温度场变化方程。通过能量守恒定律,可以导出温度场变化方程[20-21]:

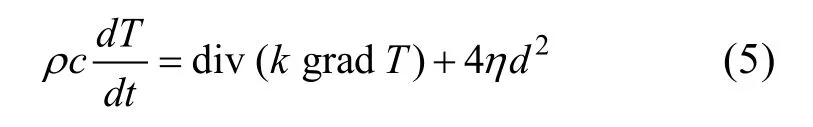
其中,T是温度,ρ是密度,c是比热,k是热导系数,4ηd2表示应变加热。比热c与热导系数k由温度决定:

由于冰的温不能超过压力融点温度,所以为求解温度场变化方程(5)还需边界条件的约束,也就是T≤Ta(Ta压力熔点温度)。

在获取Stokes 方程以及温度场变化方程后,必须对冰盖的上表面和下表面添加适当的边界条件,才能求解所需的所有方程。

冰盖上表面被称为自由表面。因为其仅与大气接触,忽略大气压力和风应力,本文假定冰盖表面应力为0,则冰盖上表面相当于可以自由运动。冰盖上表面Fs(x,t)表达式如下:

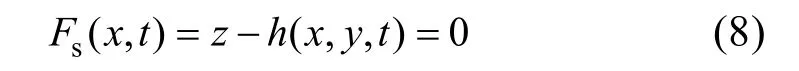
冰盖上表面运动学边界条件方程如下:

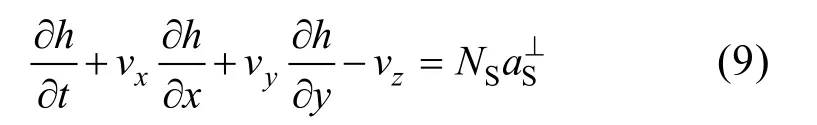
式中,NS为Fs(x,t)的梯度模,aS⊥为冰盖上表面流量。

除此之外冰盖还存着温度场的边界条件问题,其表达式如下:

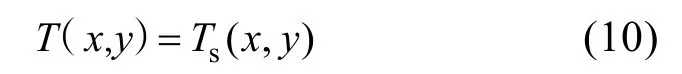
其中,Ts表示冰盖上表面的温度,需要预先给出其数值并且该值一般低于0℃。

同理,冰盖下表面也存在着动力学边界条件,冰盖下表面Fb(x,t)表达式如下:

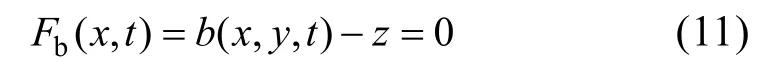
冰盖下表面运动学边界条件方程如下:

Nb为Fb(x,t)的梯度模,ab⊥为是冰盖底部冰流通量。

其中,为地热通量,k为热导系数,T为冰盖下表面温度,n冰盖下表面法向量,t为冰盖下表面应力场,vb为冰川底部流速,ρ是冰密度,L为冰的潜热。地热通量作为输入参数需事先给出。

2 研究区域概况、边界条件以及数据来源

2.1 研究区域概况

玛丽伯德地位于西南极洲罗斯冰架和罗斯海以东,太平洋以南。向东延伸大约到罗斯冰架顶端和爱兹海岸之间,它的长度在 158°W 到103°24′W 之间,大部分为冰盖所覆盖,目前已经显示出冰盖质量下降的迹象[4-5]。

玛丽伯德地的研究对整个西南极的研究有着十分重要的意义。1998年12月至1999年1月调查人员通过Twin Otter 飞行器在地表300 米以上使用雷达和激光测高仪测量,得到玛丽伯德地冰盖表面和冰床的高程数据。Luyendyk 等[22]研究表明罗斯海裂谷的基岩变薄、扩张的大陆地壳形成了西部的玛丽伯德地和东部的罗斯冰架。2005年Maule等[23-24]绘制了整个南极区域的地热通量图,发现玛丽伯德地附近的地热通量在100 mW·m-2左右。2007年至2009年,Rignot等[25]利用合成孔径雷达模拟了整个南极的冰流速度,得到玛丽伯德地区域的表面冰流速,发现伯德冰川的冰流源于四条向内陆延伸的支流。Hermann 等[26]通过实地钻孔测量发现,西南极洲Siple Dome 的垂直温度剖面显示出了地热通量升高。目前为止对于该地区的研究很多都是在整个南极的尺度上进行的,对该区域的专门研究较少。

本文的研究区域(76.8°S～77.3°S,138°W～ 142°W)宽度为50 km,长度为100 km,位于玛丽伯德地的西部,靠近福特山脉以及苏兹伯格冰架,如图2 所示。图2a 红色方框为本文的研究区域,设置原点为(76.8°S,142°W),纬度增大方向为x轴,经度减小方向为y轴; 图2b 为经过数据预处理后使用三维有限元网格生成器 G m s h 和 Elmer/Ice 冰盖模式模拟的研究区域表面高程网格图,研究范围区域较小,采用三角网格划分,可以更加精确地研究其动力学特征。图中的(x,y)坐标表示到原点的距离,即研究区域的宽度和长度。文中通过使用Elmer/Ice 冰盖模式得到了研究区域的表面和底部的温度场、速度场和应力场,并对相关结果进行了分析。

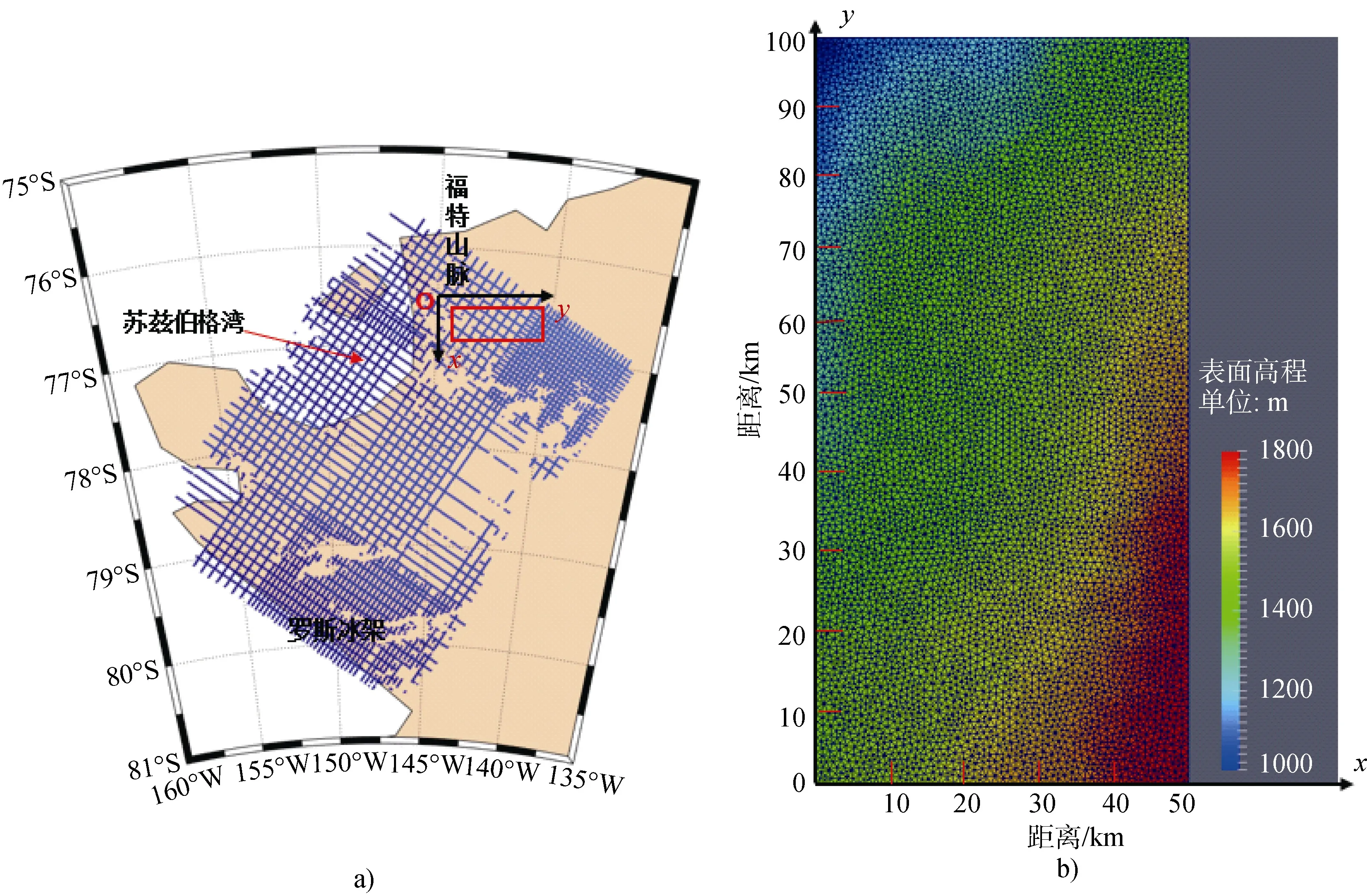
图2 研究区域位置及表面网格划分.a)位置示意图; b)区域的网格图Fig.2.Study area grid and location map of the domain.a) location diagram; b) grid map of the domain

2.2 边界条件

本文的边界条件包括表面温度、底部滑动定律、底部地热通量、侧边界条件和上下表面高程。

2.2.1 表面温度

Hermann 等[27]于1998年到2001年之间利用热水钻探技术,在西南极获得了22 个钻孔的温度剖面测量结果,利用这些数据的表面温度和对应的高程通过线性拟合得到了研究区域的表面温度(T)和高程(H)关系:

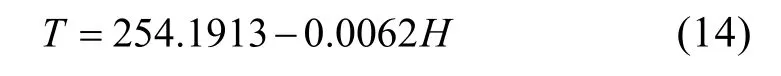
2.2.2 底部滑动定律

本文采用Weertman 滑动定律,具体形式为:

其中σnti是基础剪切应力,ub为底部滑动速度,的标准形式,βm为底部滑动参数,m为指数,uti是基础速度。

2.2.3 底部地热通量

根据Maule 等人[23-24]在2005年绘制的整个 南极区域的地热通量图,本文将玛丽伯德地的地热通量设置为100 mW·m-2。

2.2.4 侧边界条件

研究区域周围边界压力条件,公式如下:

假设水平温度梯度为0,既水平方向热通量为0。

2.2.5 上下表面高程数据集

冰盖表面和底部高程数据来自美国国家冰雪数据中心(NSIDC),该数据集提供了西南极玛丽伯德地西部的部分的地表高程和冰厚数据,包括福特山脉、苏兹伯格冰架、爱德华七世半岛的大部分地区和罗斯冰架东部的谢里斯海岸地区。调查人员使用雷达探测和激光测高仪在300 米以上的高空通过 Twin Otter 飞行器在1998年12月至1999年1月共进行了64 次飞行调查。该数据集中,大部分地区的测线间距为5.3 km,同一条测线上点间距为11.7 m,垂直于测线方向的空间分辨率较低,本文对其进行线性插值,得到了空间分辨率为500 m 的高程数据。

根据边界条件的设定和输入的表面和底部高程,最终得到研究区域的表面温度,底部高程和表面高程如图3 所示。

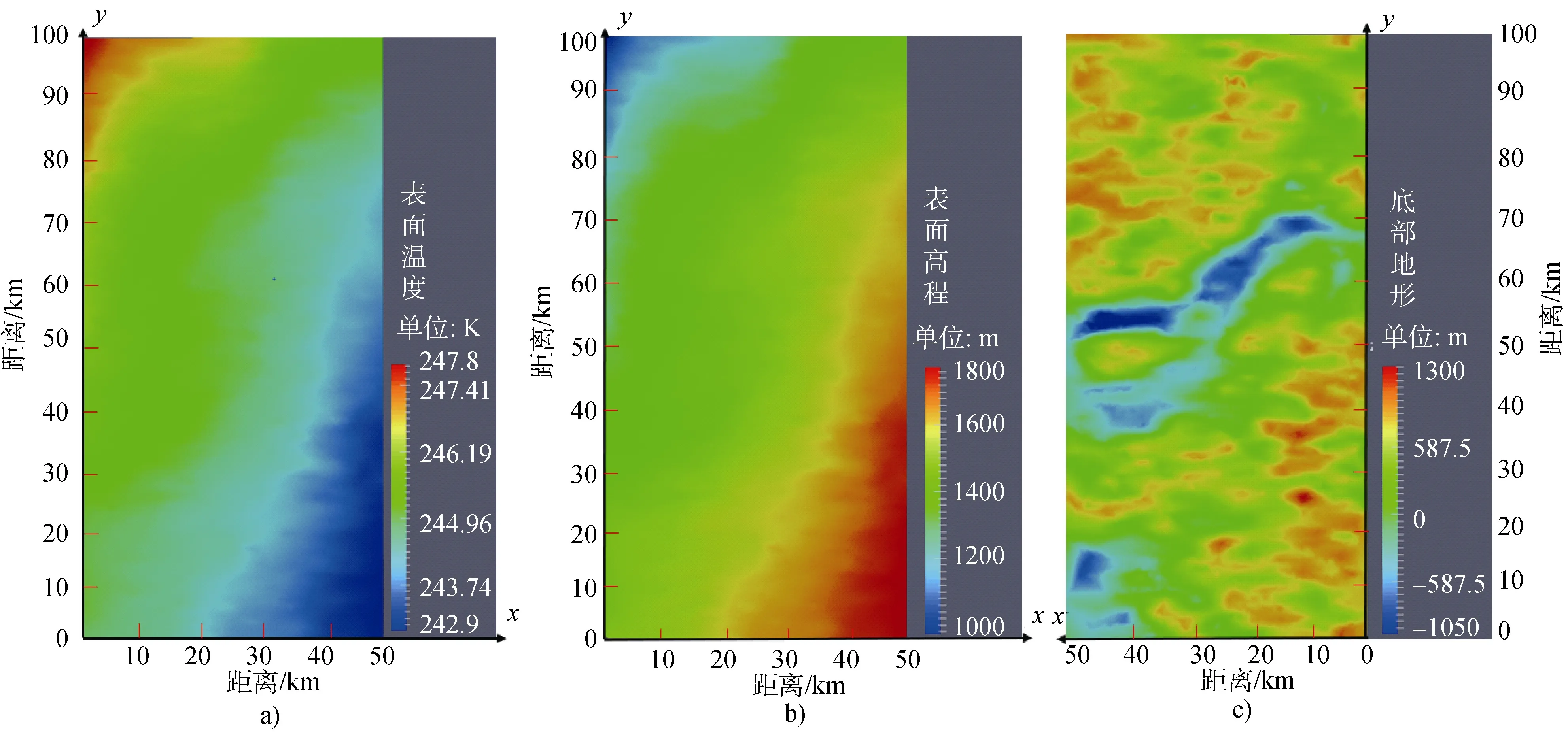
图3 研究区域的冰盖表面温度(a)、冰盖表面高程(b)和冰盖底部地形(c)Fig.3.a) Ice sheet surface temperature; b) surface elevation; c) bottom topography of the modelled domain

3 模拟结果与讨论

3.1 冰盖温度场

图4a 为研究区域冰盖表面的温度场结果,其温度范围为242.9～247.8 K,而且上表面有明显的变化梯度,与图3b 的表面高程变化梯度正好相反,冰盖温度随高程的增加而变小。

图4b 为研究区域冰盖底部的温度场结果,可以看到研究区域冰盖底部大部分区域都达到了压力融点,只有一小部分未达到压力融点。这可能与研究区域的地形有关,因研究区域靠近福特山脉,冰盖的运动会受到山脉的阻挡而出现较大的垂向速度,影响底部的温度场[8]。

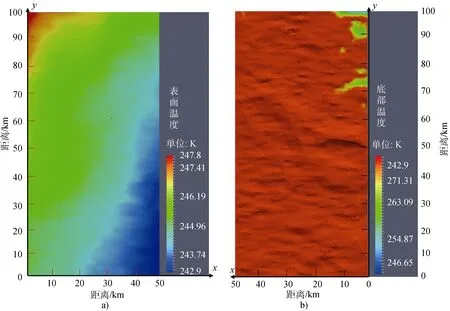
图4 研究区域温度场.a)冰盖表面温度场和b)冰盖底部温度场Fig.4.Temperature fields of the study area.a) surface; b) the bottom

冰盖的底部温度会受到地热通量的影响,本文同时分别模拟了地热通量为80 mW·m-2和120 mW·m-2时的底部温度场。如图5 所示,不同的地热通量对底部温度场影响不大,与孙波等[13]提到的地热通量对冰盖内部瞬变的热性质影响不大的结论一致。图3a 表明该区域的冰盖表面温度较低; 另外由于该区域冰盖底部地形复杂、网格分辨率和精度都较低[8],这两个问题可能是压力融点和地热通量的关系出现误差的主要原因。

图5 地热通量为80 mW·m-2 时的底部温度场(a); 地热通量为120 mW·m-2 的底部温度场(b)Fig.5.Bottom temperature fields with different geothermal fluxes.(a) 80 mW·m-2; (b) 120 mW·m-2

3.2 冰盖流速场

图6a 为研究区域冰盖表面流速场的模拟结果,箭头代表冰流速的方向。可以看到冰盖表面冰流速范围为0.012～744.7 m·a-1,其高流速区域对应着地形较高的区域或者地势较低的峡谷,该结果与Rignot 等[25]使用卫星和雷达绘制的整个南极冰流速在尺度上相当。结合图2b 可以发现冰盖表面的冰大致上由地势较高的区域流向地势较低的区域。图6a 左红色框内冰流向相反方向流动,因为此处地形相对于周围区域较高; 图6a 右红色框内中间地势较低,故冰流由两边向中间汇聚。图6b 为冰盖底部流速场的模拟结果,可以看到在冰盖的下表面流速接近0 m·a-1,可能是冰盖底部粗糙度太大[28],阻碍了冰的流动。

图6 研究区域表面流速场(a)和底部流速场(b)Fig.6.Velocity filed of surface (a) and bottom (b) of the study area

图7是研究区域冰盖表面速度场x-y-z分量的模拟结果。从图7a 中可以看到x分量方向冰流速为-545.2～11.04 m·a-1; 从图7b 中可以看到y分量方向的冰流速为-88.81～165 m·a-1; 从图7c 中可以看到z分量方向冰流速为-128.1～744.6 m·a-1。图7 表面冰流速最大的地方在x-y-z分量方向表现出了不一致性,x方向和y出现负值,z方向出现最大值,但是表面冰流速却表现出了和z分量方向一样的最大值,说明研究区域表面冰流速受垂直方向影响较大,而水平方向(x,y)对其影响较小。

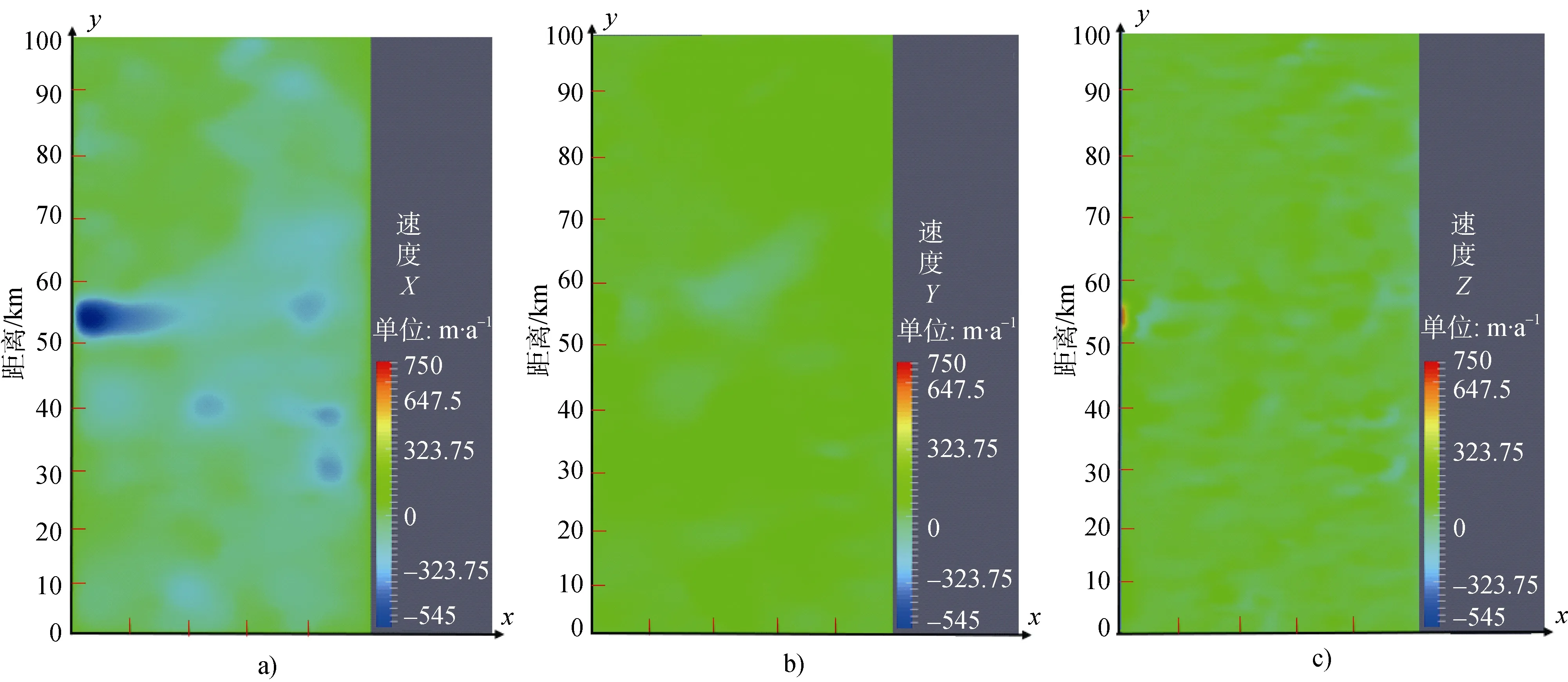
图7 x 方向表面流速场(a)、y 方向表面流速场(b)和z 方向表面流速场(c) (尺度未同一)Fig.7.Velocity filed along x-direction (a),y-directionand (b) and z-direction with nonuniform scale (c)

图8 统一了冰流速尺度范围,发现冰流速最大值出现在山峰或者峡谷区域,也可以更直观的看到在冰流速最大的地点,垂直方向对其表面速度的影响是较大的。

利用Bedmap2,图9 给出了(77.3°S,142°W)和(77.3°S,138°W)两点之间的垂直剖面图,该测线经过图8c 中z方向速度最大值的点(即y轴)。从图9可以看到,z方向速度的最大值出现在冰下深谷对应的表面。

图8 x 方向表面流速场(a)、y 方向表面流速场(b)和z 方向表面流速场(c)Fig.8.Velocity filed along x-direction (a),y-direction (b),and z-direction with uniform scale (c)

3.3 冰盖应力场

图10a 为冰盖表面的应力场,其压强范围在-0.1316～0.1514 N·m-2。图8c 表面冰流速达到最大值的位置,对应了图 10a 中表面压力最大值的位置。通过图9 可以看到在冰下深谷的位置,冰流速向下分量较大,从而也产生了更大的压强。

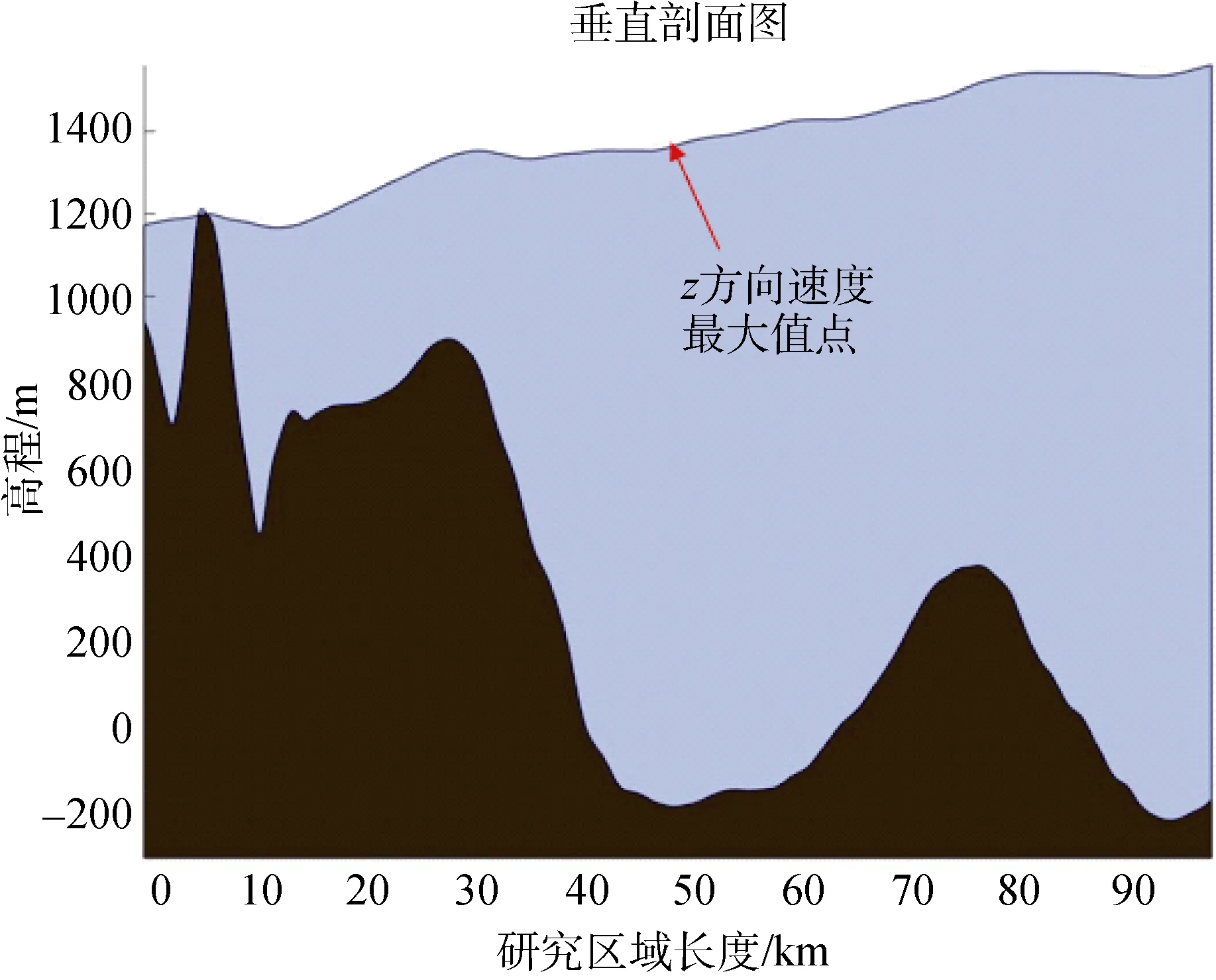
图9 样本测线高程剖面图Fig.9.Profile elevation diagram of sample survey line

图10b 为冰盖底部应力场,其压强范围在-0.1316～21.87 N·m-2。结合图3b 和图3c 可以发现 该区域冰盖较厚,故底部压力数值较大,冰盖厚度越大的地方其对应的应力场也越大。结合图4b可以发现,在压强范围较小的地方其底部的温度场未达到压力融点。由此可以推断,冰盖底部温度场较小的区域,对应的应力场也较小[2]。

图10 冰盖表面应力场(a)及底部应力场(b)Fig.10.Stress field on the surface (a) and the bottom (b) of the ice sheet

4 结论与展望

本文研究利用NSIDC 提供的关于玛丽伯德地西部区域表面和底部的高程数据,进行插值处理后,获得该区域详细的地形数据,结合相关文献中的表面温度及地热通量等边界条件,利用Elmer/Ice 冰盖数值模式对玛丽伯德地西部区域进行模拟,获得了该区域表面和底部的温度场、速度场和应力场信息。研究表明该研究区域的冰盖底部大部分区域都达到了压力融点,仅一小部分区域未达到压力融点。讨论了三种不同地热通量(80 mW·m-2,100 mW·m-2,120 mW·m-2)对模拟结果的影响,结果表明不同地热通量对底部温度场的影响不大。本文研究模拟得到冰盖表面冰流速范围为0.012～744.7 m·a-1,该结果与Rignot 等[25]绘制的整个南极的冰流速在尺度上相当。冰盖表面的冰总体上由地势较高的区域流向地势较低的区域,推测是较大的冰盖底部粗糙度阻碍了冰的流动,使得冰盖底部速度接近于0 m·a-1。此外通过分别从x-y-z三个方向对表面冰流速进行分析,发现冰流速最大值出现在山峰或者峡谷所对应的表面。通过垂直剖面图可知,z方向的速度在冰下深谷上方达到了最大。应力场的结果表明,冰盖厚度越大的地方其对应冰盖底部应力场也越大。

冰盖的温度场、速度场和应力场不仅与地热通量和表面温度相关,还受到冰盖随时间的变化和积累率的影响。由于缺乏详细的实测数据,本文仅研究了三个不同地热通量对底部温度场的影响,未来随着南极科考对玛丽伯德地的深入研究,将进一步讨论该区域温度场、速度场以及应力场与冰盖厚度随时间变化的相互关系以及与积累率之间的关系。