对数非线性薛定谔方程基态解的数值解法

冯子旭， 何维清， 张世全

(四川大学数学学院， 成都， 610064)

1 引 言

玻色-爱因斯坦凝聚态(BEC)[1]是由微观粒子的量子特性引起的宏观现象[2-5].在最近的物理实验中，物理学家把不同组分的BEC混合在一起，使这些BEC 结合在一起形成量子液滴(液滴态).液滴态[6]可以用波函数描述，满足如下的对数Gross-Pitaevskii方程(LogGPE)：

(1)

这里x是空间变量，t是时间变量，Ω>0是角速度，β,σ是刻画粒子间相互作用类型的参数，角动量算子Lz和势函数V(x)定义如下：

Lz=-i(x∂y-y∂x),

这里的d代表空间维度.

对于该对数非线性薛定谔方程，在实际应用中我们主要关心其基态解和动力学演化，本文的研究目标就是构造该方程基态解的数值解法.另一方面，对于经典的非线性薛定谔方程基态解的研究已有丰富结果，如,对数非线性薛定谔方程(LogSE)基态解的存在性可以参考文献[7].

在非线性薛定谔方程基态解的计算方面，Edwards和Burnett[8]用Runge-Kutta方法求解了一维和三维球对称基态解；Chiofalo 等[9]类比动力学计算方法提出了虚拟时间演化法；Bao和Tang[10]提出利用有限元法直接极小化带质量约束的能量泛函，进而得到基态解；Bao[11-13]等结合梯度流和单位球投影方法提出了归一化梯度流方法，并构造了向后欧拉差分和向后欧拉谱方法，在适当初值下有效计算了基态和激发态.值得注意的是，这些方法都是针对非对数非线性薛定谔方程的.众所周知，由于对数非线性项的奇异性，这些方法并不能直接应用到对数非线性薛定谔方程基态解的计算.本文将基于正则化能量泛函和归一化梯度流构造一种求解对数非线性薛定谔方程基态的数值方法.

本文剩余部分安排如下.第2节介绍方程(1)的基态定义和物理意义及带正则化参数1<ε≪0的正则化方法.第3节给出了具体的数值方法和计算过程.第4节我们用数值算例验证方法的可靠性.最后，第5节给出全文的结论.

2 预备知识

方程(1)有两个重要的相关物理量，分别是能量和质量，定义如下：

(2)

(3)

其中

(4)

数学上，基态解φg(x)是能量泛函在质量约束条件下的极小值点，即

(5)

由于对数非线性项的奇异性，即当ρ→0+时,logρ→-∞，我们不能直接使用前文的方法.为了解决这个难题，我们参考正则化(ERLogSE)方法[14]，对能量泛函的对数项引入正则化参数ε进行修正，修正后的能量泛函为

(6)

其中正则化函数

或

(7)

根据正则化能量泛函，我们有如下的正则化方程：

fε(ρ)=(Fε(ρ))′

(8)

(9)

对于上式所得的基态解能量与原问题的基态解能量的误差，我们有下面的定理.

(10)

证明 首先，∀φ∈S∩H1，有

利用不等式0≤log(1+x)≤x，∀x≥0可得

-Cε≤E(φ)-Eε(φ)≤0.

根据基态的定义可知，

综合上述不等式即可得到定理2.1.

3 数值解法

为求解(5)式的能量泛函极小化问题，我们首先对(1)式使用虚时演化：t→-it,再利用离散归一化梯度流(DNGF) 方法.

选择一个固定的时间步长Δt>0.对n= 0,1,2, …和一个时间序列tn=nΔt，在每个时间步t∈[tn,tn+1)，DNGF 方法如下：

⑬据墓志，韩显宗卒于太和二十三年，时年三十四岁。参见赵超《汉魏南北朝墓志汇编》，天津古籍出版社2008年版，第39页。

fε(|φε|2)φε,x∈Rd

(11)

(12)

φε(x,0)=φ0(x),x∈Rd，

(13)

i) 对无约束条件的能量泛函使用速降法;

ii) 为了满足约束条件，在每个时间步将解拉回到解空间S.

接下来我们用向后欧拉傅里叶谱(BFFP) 方法来离散(11)～(13)式.由势函数的性质，(11)～(13)式的解会在无穷远处呈指数衰减到零，所以在实际计算时我们可以把计算区域截断到一个合适的有界区域上，并假设解满足零边界条件.不失一般性，我们以二维的BFFP方法为例，对其它维数来说也是类似的.

在二维的情况下，对(11)～(13)式的截断问题如下：

fε(|φε|2)φε,x∈D,t∈[tn,tn+1)

(14)

(15)

φε(x,t)=0,x∈Γ=∂D,t∈[tn,tn+1)

(16)

φε(x,0)=φ0(x),x∈D且有

(17)

这里的计算区域D=[a,b]×[c,d]，其中|a|， |b|，|c|和|d|是足够大的常数.选择空间网格，其中J和K是两个正偶数，网格点如下：

定义下标集

TJK=(j,k)|j=1,2,…,J-1,

k=1,2,…,K-1,

k=0,1,2,…,K.

引入记号

则求解(14)～(15)式的BFFP方法离散格式为[11，15]：

(18)

(19)

对Δ，∂x和∂y,我们可以使用傅里叶谱方法逼近，即

(20)

(21)

(22)

在每一个时间步，为了求非线性方程组(18)式的解φε,(1)，我们使用带稳定参数项的离散傅里叶变换方法，迭代求解下面的线性方程组,直至收敛：

iΩyk([∂x]φε,(1),m)jk-iΩxj([∂y]φε,(1),m)jk-

(23)

对(23)式两边使用离散傅里叶变换，有

(24)

(25)

的φε,(1),m+1即为当前时间步的解φε,(1).

4 数值模拟

表1 对不同参数β，两种正则化方法得出的基态解能量及能量之差Tab.1 The energy and energy difference of the ground state solution obtained by two regularization methods for different β

由上表可知，在数值上来说两种正则化方法的结果几乎没有区别.因此，在后面计算二维情况的基态解时我们统一使用第一种正则化方法.

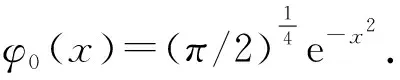
从上图1可知，左图的正则化方法能量关于参数ε的收敛阶高于一阶，略低于三阶;而右图的正则化方法能量关于参数ε的收敛阶高于一阶，非常接近二阶,与理论分析相符，并且数值试验的结果优于理论结果.再由上表2可知，计算耗时基本不受正则化参数大小的影响.所以在求解基态时我们可以选择尽可能小的正则化参数.

表2 对不同的正则化参数ε，两种正则化方法得出的基态解的运行时间Tab.2 Running time of the ground state solution obtained by the two regularization methods for different ε

下面我们用第一种正则化方法来研究在正则化参数ε=10-14时的质量M0和能量E0随计算时间t的变化，结果如下.

根据图2，我们可以看到该数值方法在此算例中是质量守恒，能量稳定的.

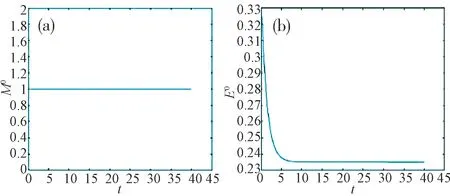
图2 质量M0随时间的变化(a);能量E0随时间的变化(b)Fig.2 The change of mass M0over time(a), and the change of energy E0 over time(b)

最后，应用前面提出的数值方法计算LogSE的基态解.如文献[6]，我们设置各参数为：M=1 000,γx=γy=γ=0.04,β=1,σ=1,D=[-30,30]×[-30,30].我们选择如下函数的线性组合作为初始函数[16]：

φ(x)=C|x|ke-γ|x|2/2+ikθ,

θ(x,y)=arctan(y/x),

C是归一化常数，使得‖φ0‖2=M.我们研究如下四种情况：

Case 1 Ω/γ=0,φ0(x,y)=Ce-γ|x|2/2;

Case 2 Ω/γ=0.375,

φ0(x,y)=C(x+iy)e-γ|x|2/2;

Case 3 Ω/γ=0.45,

φ0(x,y)=C|x|e-γ|x|2/2+iθ;

Case 4 Ω/γ=0.5125,

x1=(5,0)T,x2=(-5,0)T,

x3=(0,-5)T.

进一步，我们取选择非常小的正则化参数ε=10-14，时间步长Δt=0.001以及网格J=K=28，计算结果如下.

图3 (a～d)依次为Case 1～4的基态解Fig.3 From (a) to (d) are the ground states of Case 1～4

我们的计算结果与文献[6]中的结果相符，这说明了我们的方法的可靠性.

5 结 论

本文提出了带正则化参数的ERLogSE方法，解决了对数非线性项在原点处的奇异性带来的困难，并分析了正则化基态解与原问题基态解的能量误差估计.基于正则化的能量泛函，本文设计了相应的求基态解的数值格式，并用数值算例验证了方法的可靠性和理论分析的正确性.