基于均匀化理论的水合物沉积物修正Duncan-Chang本构模型
王辉,周世琛,陈宇琪,周博,薛世峰
(中国石油大学(华东)储运与建筑工程学院,山东青岛,266580)
天然气水合物是在高压低温条件下由天然气分子和水分子形成的类冰状白色晶体化合物,主要存在于陆地高寒永久冻土地区或深海海床下[1]。由于具有储量巨大、能量密度高以及绿色无污染等优点[2],天然气水合物的开发和利用受到越来越多国家的关注与重视。然而,目前开采所广泛采用的降压法和注热法会引发天然气水合物的大量分解,由此产生的孔隙水和气体会引起超孔隙压力,降低储层强度,从而引发井壁垮塌、海底设施地基失稳以及海底滑坡等灾害[3−5],因此,研究水合物沉积物的强度和变形,建立更加精细化的本构模型对于天然气水合物的安全开采具有重要意义。
目前国内外学者在室内水合物沉积物三轴试验的基础上提出了大量的本构模型。按照不同学者对水合物沉积物组成的认识,可以将本构模型的研究思路分为2类。
第1 种将水合物沉积物的看作均质岩土材料,天然气水合物主要影响材料内部状态的变化,在非线性弹性理论和弹塑性理论框架内,建立水合物沉积物的本构模型。PINKERT等[6]认为水合物对沉积物的黏聚力、内摩擦角以及剪胀角有着较大的影响,从而发展了水合物沉积物的Mohr-Coulomb(摩尔−库仑)弹塑性本构模型。然而摩尔−库仑模型只能考虑剪切屈服而无法考虑体积屈服的变化。UCHIDA 等[7−8]引入土的临界状态理论,认为水合物的存在导致了屈服面改变,从而建立起水合物沉积物的临界状态模型。此外,SHEN等[9−10]认为水合物改变沉积物骨架的状态参量,进而影响整个沉积物的力学响应。基于此,建立了水合物沉积物的状态相关本构模型。这类研究思路对于本构的建模较简单,对于弹性参数的计算多采用经验拟合公式,并不具有普遍适用性。
第2类研究思路则认为水合物沉积物是由水合物固态颗粒和沉积物基质颗粒组成的两相复合岩土材料,而水合物沉积物的变形则是由水合物颗粒与沉积物骨架颗粒共同作用的结果。吴二林等[11−13]将土骨架颗粒看作基相,水合物作为夹杂相,基于复合材料混合律理论推导了水合物沉积物的等效弹性模量与等效泊松比,并引入损伤力学理论与概率统计方法建立了水合物沉积物的损伤统计模型,该模型能够较好模拟由于水合物胶结破损引起的应变软化,但该模型并不能预测沉积物的体积变形;SANCHEZ等[14]认为水合物沉积物的力学响应是水合物胶结和颗粒之间的摩擦共同作用的结果,从而引入弹性损伤模拟水合物的胶结破损,采用临界状态模型模拟沉积物骨架的塑性变形,建立水合物沉积物的复合体弹塑性损伤模型,这种模型虽然能够较好地解释水合物沉积物的变形机制,但是由于引入较多反映微观的变形参数,而且无法从现有试验数据中获得,导致参数确定和数值实现困难。
目前,Duncan-Chang 本构模型因为其参数确定简单、数值实现容易,在实际工程中应用较广。MIYAZAKI 等[15−17]基于原始Duncan-Chang 模型,将水合物沉积物的强度和刚度看作水合物饱和度、温度和分解时间的函数,提出了水合物沉积物非线性本构模型,然而这些模型只能预测在低水合物饱和度、高围压条件下的应变硬化现象,而无法模拟在高饱和度、低围压条件下的应变软化现象。基于此,首先,通过修正原始Duncan-Chang模型,使之既能够模拟应变硬化现象又能模拟应变软化现象;其次,将水合物沉积物看作是一种由天然气水合物颗粒作为夹杂相,沉积物骨架作为为基相的非均质复合岩土材料,基于Mori-Tanaka 均匀化理论提出一种水合物沉积物等效弹性参数的有效预测方法;第三,考虑水合物胶结对沉积物骨架侧向应变的影响,提出水合物沉积物的侧向应变预测模型。最后,探讨模型参数的物理意义,并将模型预测结果与室内三轴试验结果进行对比,验证模型的适用性。
1 修正Duncan-Chang本构模型
1.1 Duncan-Chang模型的修正
原始Duncan-Chang 模型是Duncan 和Chang[18]在总结重塑土的三轴试验数据总结出的数学拟合方程,其假设重塑土的偏应力σ1-σ3−应变ε1关系服从双曲线关系:

式中:a和b为模型的拟合参数。该模型能够较好模拟重塑土的非线性和压硬性,然而对于具有应变软化特性的土体的预测效果较差。
图1所示为室内水合物沉积物三轴试验偏应力−应变曲线[18]。由图1可见:当饱和度为0即试样为纯砂试样时,其偏应力−应变曲线经历较小的弹性阶段便过渡到屈服阶段,随着轴向应变不断增加,又从屈服阶段过渡到塑性硬化阶段,在此过程中并未出现明显的应变软化阶段。而当试样中存在水合物时,在较低有效围压时,水合物沉积物表现出较明显的应变软化现象;而在较高有效围压时,水合物沉积物的应变软化特性则会变得不明显。MIYAZAKI 等[15]首先采用Duncan-Chang模型描述水合物沉积物的偏应力−应变特性,发现其在饱和度为0时,模型预测效果较好,而随着饱和度增大,原始Duncan-Chang 模型无法有效模拟水合物沉积物的应变软化特性。
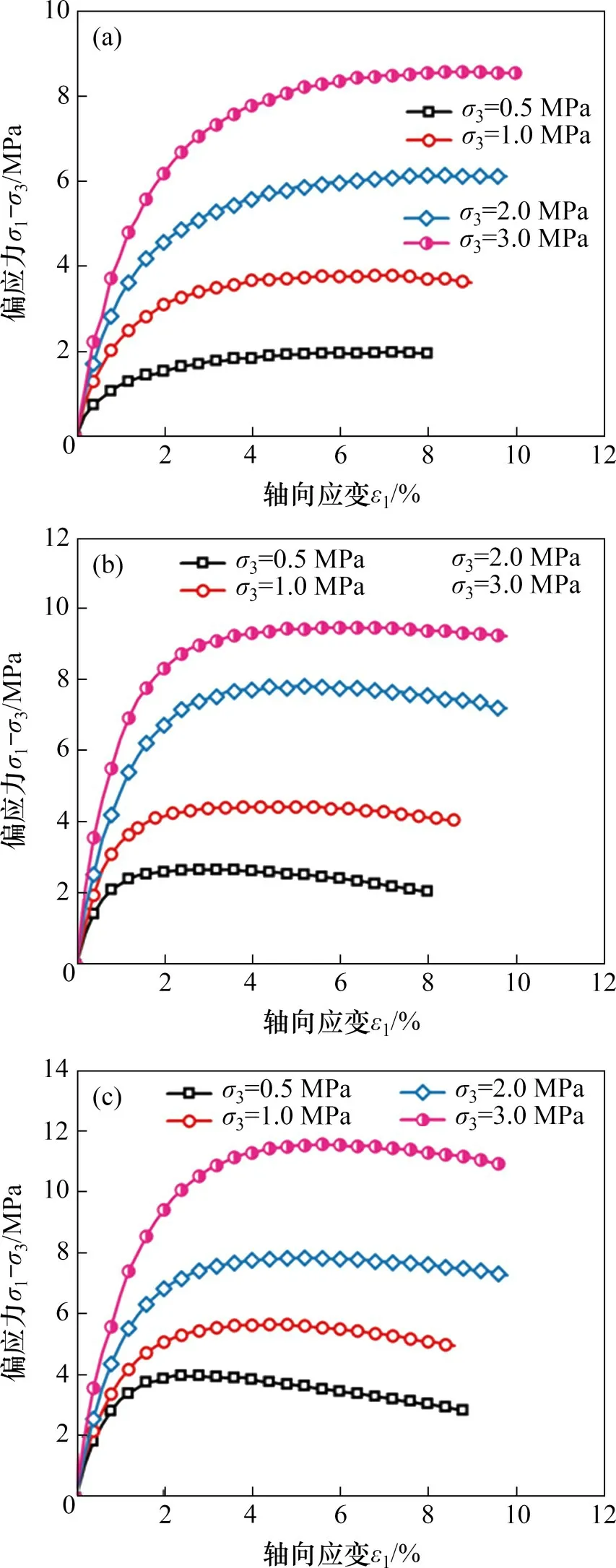
图1 水合物沉积物试样在不同有效围压条件下的偏应力−应变曲线Fig.1 Deviatoric stress−strain curves of hydrate-bearing sediments under various effective confining pressures
将水合物沉积物在不同饱和度条件下三轴试验结果进行整理,可以得到ε1/(σ1-σ3)与轴向应变ε1的关系,如图2所示。由图2可见:当饱和度为0 时,ε1/(σ1-σ3)与轴向应变ε1近似呈线性关系,这与原始Duncan-Chang 模型较一致,而当沉积物中存在水合物时,ε1/(σ1-σ3)与轴向应变ε1有着非线性函数关系,当有效围压越小且水合物饱和度越高时,这种非线性关系越明显。LAI等[19]采用二次函数描述由于冰晶引起的冻土ε1/(σ1-σ3)与轴向应变ε1的非线性关系,得到较好的预测结果。冻土虽然在形成条件和组成结构与水合物沉积物有着显著区别,但是他们在应力−应变曲线和体应变曲线都有着相似特性,所以本文仍采用二次函数关系式描述由于水合物存在而引起ε1/(σ1-σ3)与轴向应变ε1的非线性关系:

图2 ε1/(σ1-σ3)与轴向应变ε1的关系Fig.2 Relationship between ε1/(σ1-σ3)and ε1
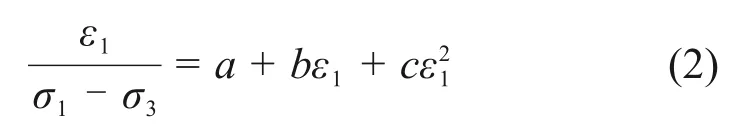
将式(2)整理即可得到既可以描述应变硬化现象又可描述应变软化现象的修正Duncan-Chang 本构模型:
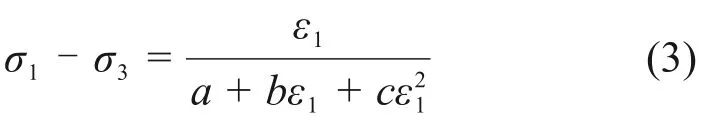
式中:a,b和c为模型参数,该模型只是在原始Duncan-Chang模型的等号右侧分母项中加了1个二次项,且只引入1 个参数c,c和ε1/(σ1-σ3)−ε1曲线的开口大小及方向有关。当c为0时,模型退回为原始Duncan-Chang模型。
根据弹性模量的定义,增量法中切线弹性模量EtHBS被定义为

在室内三轴试验中,因为dσ3=0,对式(3)进行求导则可得到水合物沉积物的切线弹性模量EtHBS

当处于试验初始点时,轴向应变可认为无限趋近于0,则该点的切线弹性模量EtHBS便可以看作初始弹性模量EiHBS,由式(6)可以得到初始弹性模量EiHBS为参数a的倒数:
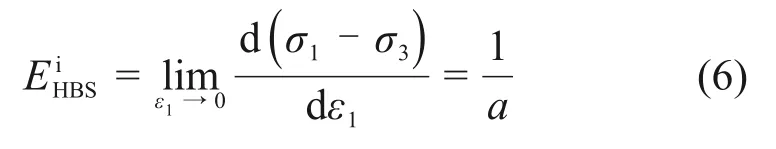
而当试验处于水合物沉积物的极限强度点m时,修正的Duncan-Chang 本构模型满足以下2 个条件:

整理式(7)和式(8)可解得模型参数b和c:


式中:(σ1−σ3)m为极限强度点的偏应力;ε1m为极限强度点m所对应的轴向应变。图3所示为应变软化现象和应变硬化现象的示意图。由图3(a)可以看出具有应变软化现象的应力−应变曲线极限强度点取应力−应变曲线的峰值点;由图3(b)可见:具有应变硬化特性的应力−应变曲线由于其应力一直是增大且逐渐趋向于某一恒定应力,所以其极限状态点取试验加载结束的状态点或者应力趋于稳定的初始值。

图3 (σ1−σ3)m和ε1m的物理意义Fig.3 Physic meaning of(σ1−σ3)m and ε1m
1.2 峰值强度与峰值应变
目前的室内试验[20]以及离散元模拟[21−22]研究表明,不论是粒间胶结型水合物、孔隙填充型水合物或骨架支撑型水合物,水合物饱和度和有效围压增加都可以显著提高水合物沉积物的峰值强度,这主要是因为有胶结作用的水合物可以将沉积物骨架颗粒联结在一起,从而限制颗粒之间的滑移和滚动;而骨架支撑型水合物除了可以与沉积物骨架一起承担荷载以外,同时和孔隙填充型水合物一样,可以增加沉积物骨架颗粒的粒间摩擦力,从而减缓了沉积物的屈服与破坏,增大了水合物沉积物的屈服强度和峰值强度。图4所示为不同围压条件下水合物沉积物峰值应力、峰值应变与水合物饱和度关系曲线。由图4(a)可见:水合物沉积物的峰值应力随着水合物饱和度增大呈非线性增加,同时,峰值应力与有效围压呈线性函数关系,所以本文采用式(11)描述峰值应力与水合物饱和度和有效围压的关系,
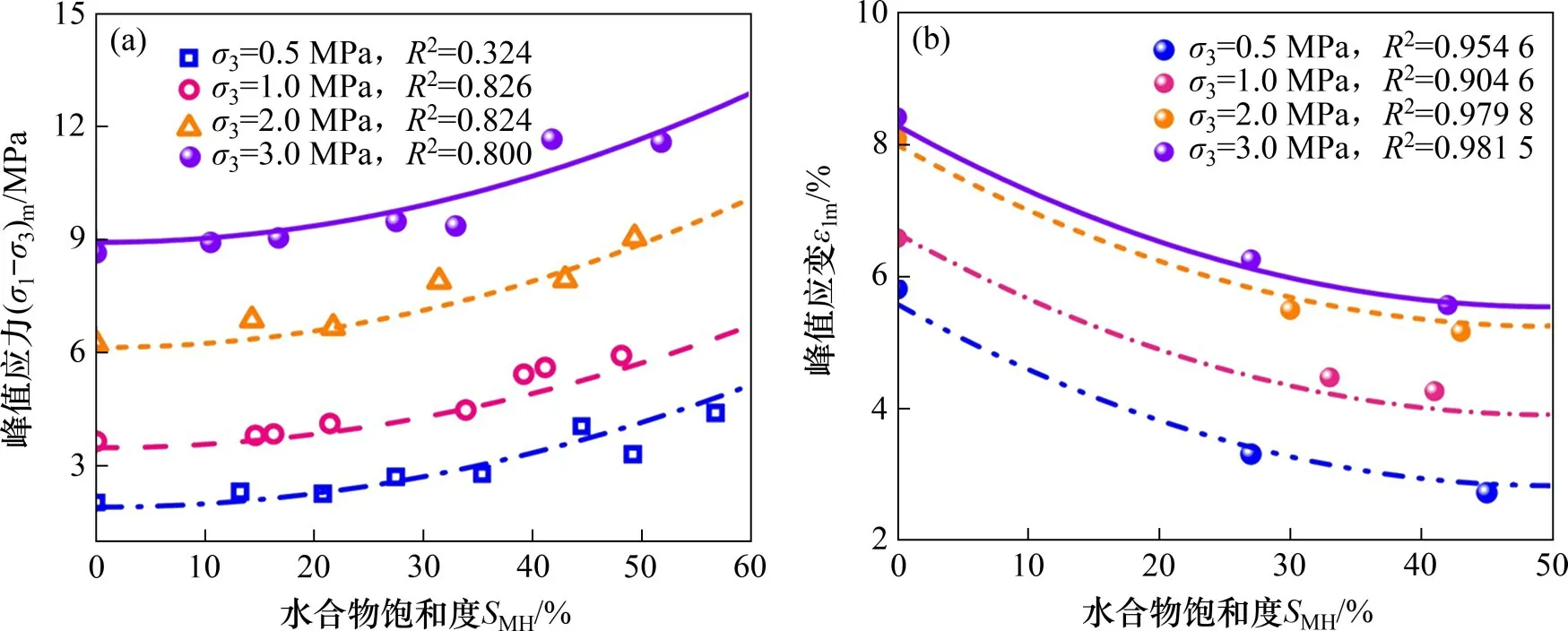
图4 峰值应力、峰值应变与水合物饱和度的关系曲线Fig.4 Relationship between peak stress,peak strain and hydrate saturation

式中:a1,b1和c1为模型拟合参数,本文通过拟合图4试验结果可得:a1=0.001 0 MPa,b1=2.79,c1=0.57 MPa。
水合物饱和度与有效围压对水合物沉积物的峰值应变也存在较大影响。由图4(b)可知:当水合物饱和度逐渐增大时,水合物沉积物的峰值应变逐渐减小,且与水合物饱和度呈非线性关系;而当有效围压逐渐增大时,水合物沉积物的峰值应变也逐渐增大,但是其增幅却逐渐减小。所以本文采用式(12)拟合峰值应变与水合物饱和度和有效围压的关系,
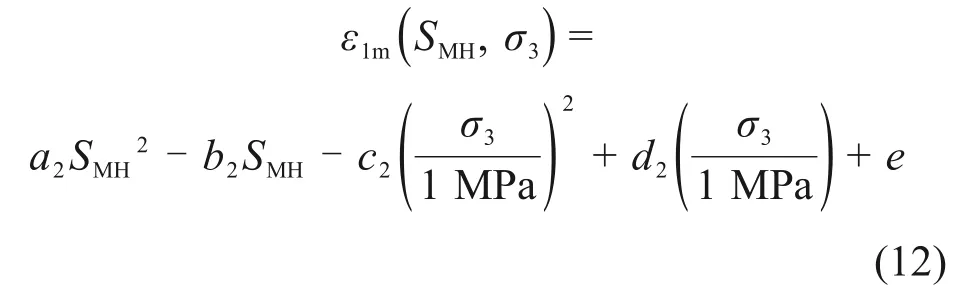
式中:a2,b2,c2,d2和e为模型拟合参数,本文通过拟合图4(b)中试验结果,可以得到:a2=0.001 1,b2=0.11,c2=0.53,d2=2.94和e=4.25。
1.3 初始弹性参数的确定
水合物沉积物可以看作由基质颗粒(砂土颗粒、黏土颗粒或两者的混合)、天然气水合物固态颗粒、孔隙水以及甲烷气组成的多相多组分岩土材料。目前室内试验所用的基质颗粒以及水合物生成方法的不同,采用试验结果拟合得到的参数并不具有普遍适用性。本文将水合物沉积物看作一种特殊的复合岩土材料,采用复合材料细观力学的均匀化理论来获得水合物沉积物的初始弹性参数。吴二林等[11]借鉴冻土中的均匀化理论,采用复合材料混合律理论获得水合物沉积物的初始弹性参数,然而,混合律理论所使用的沃伊特模型在预测弹性参数时存在较大误差,所以刘乐乐等[12]基于沃伊特模型和罗伊斯模型建立了一种新的水合物沉积物弹性参数预测方法,然而,该方法种存在参数较难确定的问题。
Mori-Tanaka 均匀化理论不仅适用于夹杂相体积分数较高的复合材料,而且给出复合材料的显式弹性参数表达式,参数确定简单且程序实现容易,目前在冻土[23]和混凝土[24]的弹性参数预测中已经获得广泛应用。所以,本文采用Mori-Tanaka 均匀化方法预测水合物沉积物的弹性参数。
在水合物沉积物的地球物理研究中,通常忽略沉积物中液态水以及甲烷气的力学作用。水合物沉积物可以看作是由体积比重较大的沉积物骨架作为基体,将简化为球形的水合物颗粒作为夹杂体的一种特殊复合岩土材料。由Mori-Tanaka 法求得水合物沉积物的等效体积模量KHBS和等效剪切模量GHBS分别为:

式中:Gs和GMH分别为沉积物骨架和水合物的剪切模量;Ks和KMH分别为沉积物骨架和水合物的体积模量;fs和fMH分别为沉积物骨架和水合物的体积分数。假设纯砂孔隙率为φ,水合物沉积物的体积为V,甲烷水合物的体积为VφSMH,沉积物基质的体积为V(1−φ),复合材料的总体积为VφSMH+V(1−φ)。可以得到沉积物骨架的体积分数fs以及水合物的体积分数fMH如式(19)所示。
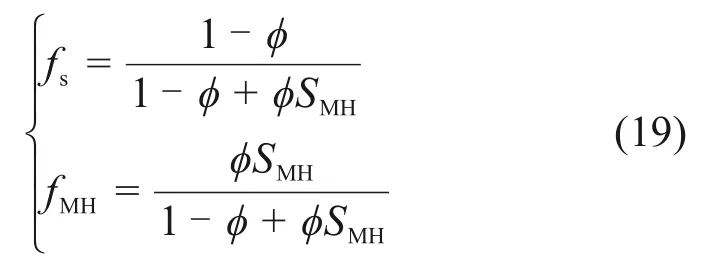
式中:SMH为水合物饱和度。由弹性力学可知,体积模量和剪切模量与弹性模量EHBS和泊松比vHBS的关系如式(20)和(21)所示。
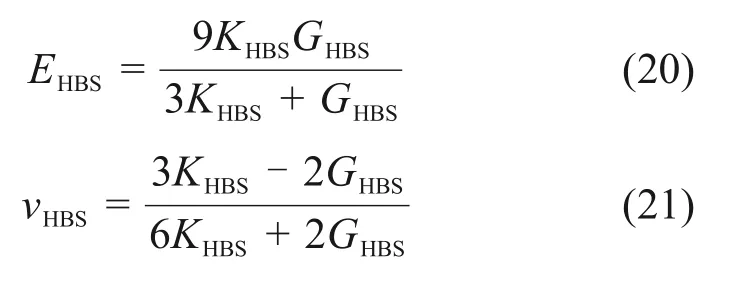
所以联立式(13)~(21)可以得到水合物沉积物的弹性模量EHBS和泊松比vHBS满足以下关系

式中,

1.4 侧向应变
MIZAYAKI等[15]采用二次函数拟合水合物沉积物的径向应变−轴向应变曲线,如式(27)所示:
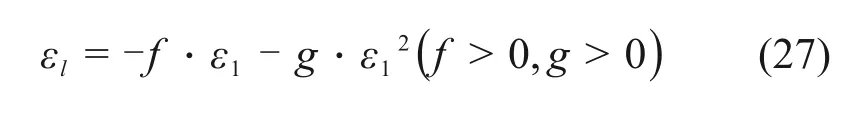
式中:f和g为模型拟合参数。试验曲线与文献[15]模型预测曲线的对比表明:当饱和度为0%即试样为纯砂时,二次函数对试验曲线的拟合效果较好,而当饱和度为27%~34%以及41%~45%时,二次函数的预测曲线往往比试验效果要小,且饱和度越大,其预测曲线与试验曲线偏差越大。造成这种情况的主要原因是:文献[15]提出的侧向应变预测模型并没有考虑水合物颗粒对沉积物骨架侧向变形的影响。本文中,将水合物沉积物看作是由沉积物骨架颗粒合水合物颗粒组成的复合岩土材料,所以在受到荷载作用时,其总变形是水合物胶结所形成的胶结元变形和沉积物骨架由于颗粒间滑移和滚动作用所产生的摩擦元变形之和。
由文献[23]可以得到水合物沉积物的代表性单元的平均应变为
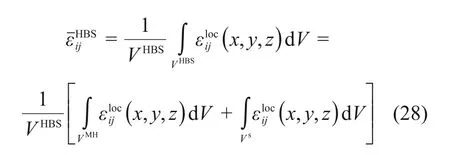
式中:为水合物沉积物代表性体元的平均应变;(x,y,z)为局部应变;VHBS为水合物沉积物的代表性体元的体积。胶结元和摩擦元的平均应变为:

式中:和分别为胶结元和摩擦元的平均应变;VMH和Vs分别为胶结元和摩擦元的体积。将胶结元的平均应变和摩擦元的平均应变式代入式(30)中,可以得到

在承受荷载作用下,水合物的胶结破损是一个动态过程,随着轴向应变增加,水合物胶结逐渐发生破损,由胶结元逐渐转化为摩擦元发挥作用,摩擦元所占的体积逐渐增大。
定义水合物胶结破损率λ为水合物发生破损的体积即摩擦元体积与沉积物代表性微元体积的比值,如式(32)所示。
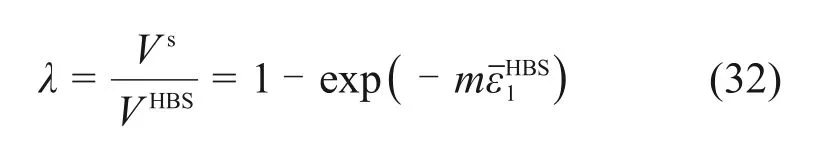
式中:m为决定水合物胶结破损速率的参数;为水合物沉积物代表性体元的轴向平均应变。将式(32)代入式(31)可以得到水合物沉积物的平均应变,

则水合物沉积物的径向应变可以表示为

在胶结元未发生破损时,将胶结元可以看作是弹性的,所以其径向应变为=vHBS,摩擦元的侧向应变可由轴向应变中的二次函数表示,从而得到水合物沉积物的径向应变为
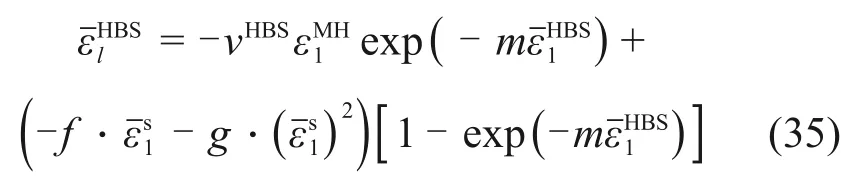
假设摩擦元的轴向应变与水合物沉积物的轴向应变关系如下:

式中:n为应变分配系数,表征摩擦元应变与水合物沉积物平均应变的关系。从而得到胶结元轴向应变与水合物沉积物的平均轴向应变的关系:

将式(36)与式(37)代入式(35)可得水合物沉积物的平均径向应变表达式:

2 模型参数的影响
模型参数的选取决定着模型预测结果的准确性,为了进一步地探讨模型参数的物理意义及对水合物沉积物强度和变形的影响,图5所示为模型参数a,b和c对水合物沉积物的偏应力−轴向应变曲线形态的影响。由图5(a)可见:当模型参数b和c保持不变时,随着a减小,水合物沉积物的初始弹性模量和峰值强度都会逐渐增大,而其对于水合物沉积物的残余强度则几乎没有影响。由式(6)可知:水合物沉积物的弹性模量等于参数a的倒数,因此,参数a主要反映水合物沉积物的刚度。
由图5(b)可见:当模型参数a和c保持不变,水合物沉积物的初始弹性模量和应力−应变曲线形态对b变化的敏感性较小,而其对峰值强度和残余强度的影响则比较明显。当b越小,水合物沉积物的峰值强度和残余强度越大,这说明参数b主要代表水合物沉积物宏观强度。
由图5(c)可见:在a和b的取值不变时,随着模型参数c增大,应力−应变曲线从应变硬化状态向应变软化状态过渡,而随着参数c逐渐减小,峰后曲线软化特性就变得更加明显,这说明参数c反映了水合物沉积物的脆性度。

图5 模型参数a,b和c对水合物沉积物的力学响应的影响Fig.5 Effect of model parameters a,b and c on mechanical response for hydrate-bearing sediments
图6所示为模型参数f,g,m和n对水合物沉积物的侧向应变−轴向应变曲线形态的影响。图6(a)给出了模型参数f对侧向应变曲线形态的影响,参数f是与沉积物基质材料相关的参数,当模型参数g,m和n取值不变时,模型参数f取值越大,则导致沉积物基质材料的侧向应变越大,从而水合物沉积物的侧向应变也随之增大。由图6(b)可知:当模型参数f,m和n取值不变时,参数g的取值变化对侧向应变形态的影响很小,可以忽略。m为决定水合物胶结破损速率的参数,由图6(c)可见,随着m增大,水合物沉积物的侧向应变也逐渐增大,说明水合物胶结破损速率也会影响水合物沉积物的侧向应变,且水合物沉积物的胶结破损速率越大,沉积物的侧向应变越大。n为沉积物骨架应变占水合物沉积物总应变的比值,由图6(d)可知,当模型参数f,g和n取值不变时,侧向应变随着模型参数n增大而逐渐增大。

图6 模型参数f,g,n和m对水合物沉积物的侧向变形的影响Fig.6 Effect of model parameters f,g,n and m on lateral deformation of hydrate-bearing sediments
3 模型验证
为了验证本文提出的本构模型的有效性,将文献[15]的结果曲线与本文提出的模型预测结果进行对比。取砂土的体积模量Ks为489 MPa,剪切模量Gs为142 MPa,孔隙率φ为37.8%。水合物的体积模量KMH为9 600 MPa,剪切模量GMH为4 300 MPa。由式(22)~(26)中可以求得水合物沉积物的初始弹性模量EHBS和泊松比vHBS。由式(6),(9)和(10)可以得到模型参数a,b和c,如表1所示。而参数f和g是与沉积物基质种类有关的参数,在文献[14]中g取决于沉积物基质的初始泊松比vs,本文中沉积物基质材料为Toyoura 砂,其初始泊松比为0.367 6;f可以由不含天然气水合物的沉积物基质的侧向应变曲线确定。n为应变分配系数,其物理意义为一个代表性体元内沉积物基质应变分量与水合物沉积物的代表性体元总应变的比值,这是一个无法直接测量的内变量,其取值范围为0~1。对于一般结构性土来说,由于胶结物质量分数很少,对于n的影响较小,所以主要是假设n为定值或将其假设为应变的Weibull 函数,采用先假设后验证的方式确定n;但对于水合物沉积物来说,由于水合物饱和度较高,n的取值与水合物饱和度有关,而由于目前室内试验结果较少,无法确定n与水合物饱和度的关系,本文为了求解方便,采用式(16)的体积之比表征应变之比,

表1 式(3)的模型参数Table 1 Model parameters of Eq.(3)
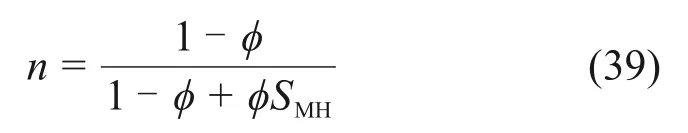
m反映天然气水合物胶结破损速率,为简单起见,假设m与有效围压无关,m随着水合物饱和度变化而变化,通过拟合不同水合物饱和度的侧向应变曲线,可以采用与水合物饱和度有关二次函数进行描述,如式(40)所示。

图7所示为不同水合物饱和度条件下,有效围压为0.5,1.0,2.0和3.0 MPa的水合物沉积物的应力−应变曲线模型预测结果与试验结果对比。由图7(a)可见:饱和度为0时,水合物沉积物的应力−应变曲线表现为应变硬化特性,本文建议的模型预 测结果与试验结果表现出较好一致性。而当水合物饱和度较高时,水合物沉积物表现出应变软化现象,且有效围压越小时,应变软化现象越明显,而本文提出的模型对于由于水合物存在而表现出的应变软化现象也具有较好预测效果,从而说明本文提出的基于均匀化理论的修正Duncan-Chang模型既能够模拟应变硬化现象又能够模拟应变软化现象,克服了MIYAZAKI 等[15]提出的水合物沉积物Duncan-Chang 模型只能预测应变硬化现象的缺陷。

图7 不同饱和度条件下水合物沉积物的应力−应变曲线数值计算结果与试验结果对比Fig.7 Comparison between model and experimental data of deviatoric stress−axial strain curves with various hydrate saturation
根据式(38)以及表2可以得到不同水合物饱和度、不同有效围压下的水合物沉积物的侧向应变计算结果,并将模型预测结果与试验结果进行对比,如图8所示。由图8可见:侧向应变的预测模型能够较好地模拟试验结果,同时,该模型考虑了水合物颗粒胶结对水合物沉积物侧向应变的影响。

表2 式(38)的模型参数Table 2 Model parameters of Eq.(38)
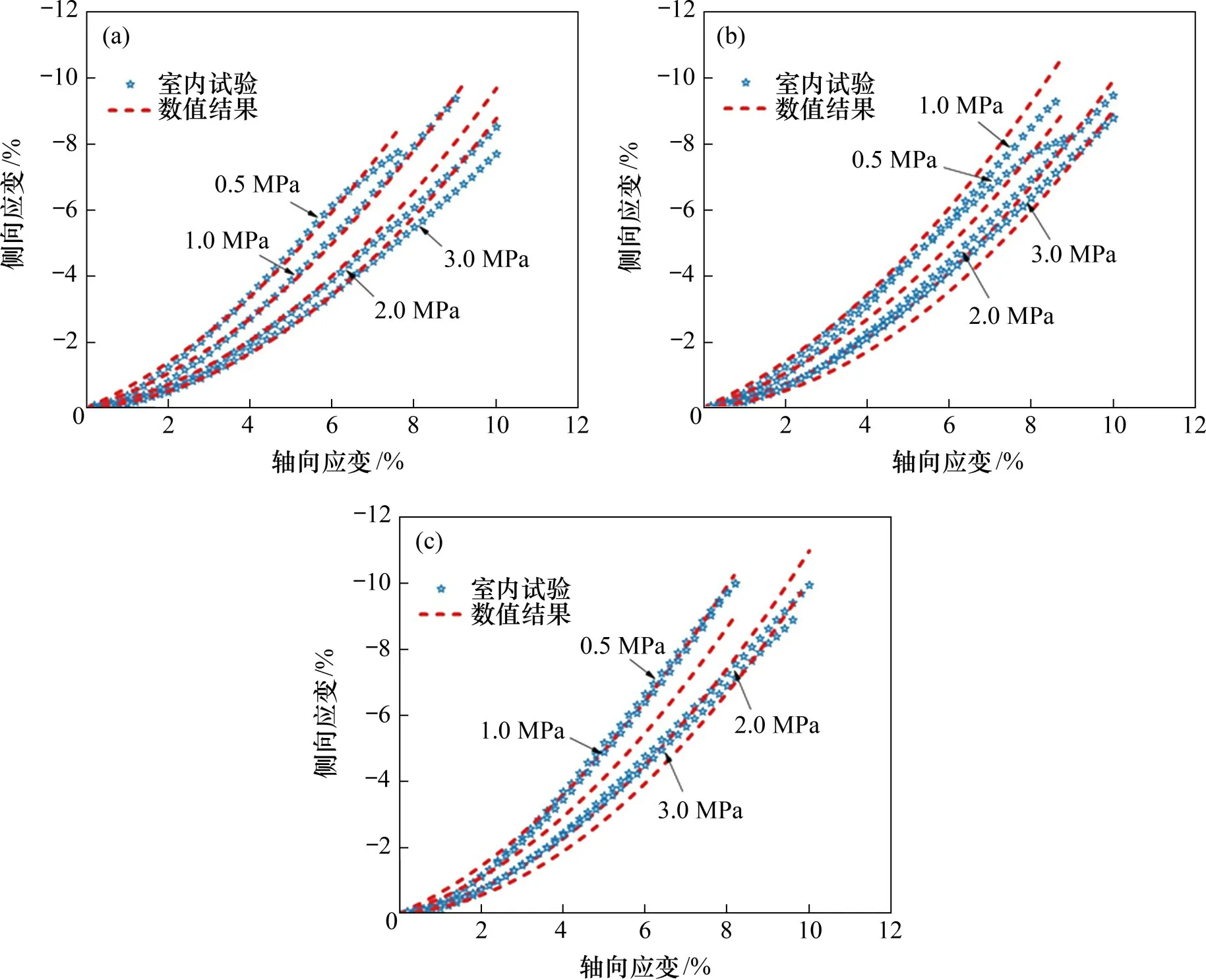
图8 不同饱和度条件下水合物沉积物的侧向应变曲线数值计算结果与试验结果对比Fig.8 Comparison between numberical results and experimental data of volumetric strain curves with various hydrate saturations
4 结论
1)基于Mori-Tanaka 均匀化方法预测水合物沉积物的等效弹性模量与等效泊松比,并在此基础上建立的修正Duncan-Chang本构模型。
2)修正Duncan-Chang 本构模型能够较好地模拟水合物沉积物的偏应力−应变曲线全过程,且能够预测在低饱和度、高围压条件下的应变硬化现象以及在高饱和度、低围压条件下的应变软化现象。
3)基于岩土材料复合体理论建立起来的水合物沉积物侧向应变模型考虑了水合物颗粒对沉积物骨架的影响,能够较好地模拟水合物沉积物侧向变形。
4)水合物沉积物在外荷载作用下的变形主要受到与水合物饱和度和有效围压有关的模型参数的综合影响:模型参数a主要反映水合物沉积物的刚度,随着参数a逐渐增大,水合物沉积物的刚度越小;模型参数b则主要反映水合物沉积物的强度,参数b越小,水合物沉积物的强度越大;参数c反映了水合物沉积物的脆性度,随着c增大,应力−应变曲线呈现出由应变硬化转向应变软化的趋势。而侧向应变主要受到模型参数f,m和n的综合影响,模型参数g的影响并不明显。

