一种水文序列变异诊断耦合模型及其应用
钱龙霞,李汉霖,汪 腾,王艺玮,王红瑞
(1.南京邮电大学 理学院,江苏 南京 210023;2.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室,北京 100038;3.北京师范大学 水科学研究院,北京 100875)
根据IPCC(政府间气候变化专门委员会)第四次及第五次报告[1–3],全球气候急剧变化,且变暖的趋势不断加强,人类活动是这一变化的重要因素。在人类活动和自然变异的双重因素影响下,世界各地水文数据的统计规律和混沌程度已经发生了显著变化[4–5]。水文序列变异诊断对防洪减灾、生态环境保护具有重要的科学意义和应用价值[6–8]。
目前,水文变异诊断方法主要用于均值变异的检测,包括Mann–Kendall法、Pettitt检验法[9–10]、Spearman秩相关检验法[11]、BG(启发式分割)算法等。国外相关的研究进展如下:兰甜[1]把常用的均值变异诊断方法划分成了5种,其中参数检验方法(如T检验和F检验)及非参数检验方法(如Mann–Kendall法和秩次相关分析法),是国内外学者采用较多的两类方法。参数检验方法对数据序列要求较高,使得非参数检验方法应用较多。Bernaola–Galván等[12]首次提出启发式分割算法(又称BG算法),适用于非平稳、非线性序列的均值变异诊断。此后,Fukuda等[13]指出BG算法对于不同统计特性的理想样本均具有良好的效果。总的来说,BG方法划分得到的各子序列能在不同的物理背景下表征其特性,避免了传统检测方法对数据序列平稳性和线性的严苛要求。国内相关的应用研究有:王生雄等[14]采用Mann–Kendall法对渭河华县站1956—2000年径流序列进行了变异诊断分析;张蔚等[15]采用Pettitt检验法和Mann–Kendall法对20世纪50年代以来珠江三角洲河网内17个主要控制水文站的年际潮差变化趋势进行了分析,所得结果与实际情况符合较好;朱恒峰等[16]采用Spearman秩相关检验法结合有序聚类分析法,推估1960—1980年代末延河流域输沙时变过程的显著干扰点,其结论与现实拟合得很好;刘秀花等[17]以Spearman秩相关系数衡量黄河宁夏段1996—2004年污染变化趋势,得到了污染程度下降的结论。虽然Mann–Kendall法、Pettitt检验法和Spearman秩相关检验法,在水文序列均值变异诊断中效果较好,但均存在明显的不足,如:Mann–Kendall法检测时会出现虚假变异点、Pettitt检验法和Spearman秩相关检验法仅适用于单点变异情形[18–20]。实际的水文序列可能存在多个变异点[21–22],BG算法能够检测出水文序列中存在的所有变异点,如陈广才等[20]采用BG算法对珠江三角洲顺德河网三水站1900—2004年的年最大洪峰流量序列进行了变异诊断,分析了BG算法在水文变异诊断的可行性,并与传统水文变异检测方法进行对比,结果显示BG算法对均值变异的敏感性和稳定性较好。
然而,除均值变异之外,水文序列还存在动力学结构变异,传统均值变异诊断方法无法刻画这种变异特征。由于水文系统是一个动态的非线性复杂系统,通过熵值的演变规律可以揭示水文要素序列演变的内在机理。何文平等[23]提出基于近似熵的变异检测新方法,即滑动移除近似熵法,能够找到动力学结构的变异区间。该方法的本质是基于近似熵曲线进行人为判断后得到变异诊断结果,具有很强的主观性,而且滑动步长(即窗口长度)L在一定范围内对近似熵曲线的形成有着重要影响,主要存在以下问题:1)较大的L易于凸显变异点附近的差异,并减弱整体的波动性,虽然增加了主观判断的可操作性,但是较大的L使得变异区间变大,变异诊断结果不精确;2)较小的L使得变异点附近的差异变小,并使整体波动性增强,增加了主观判断的难度。因此,如何对水文序列的内在演变机理进行客观诊断并给出相应的参数范围是水文序列变异诊断模型需要解决的关键问题。
综上,本文提出一种基于BG和近似熵的水文变异诊断耦合模型。首先,利用近似熵和数据滑动技术揭示水文序列内在演变机理;再利用BG算法对近似熵序列进行分割,通过置信度检验检测出水文序列存在的所有变异点;最后,通过敏感性实验给出耦合模型参数的最优取值范围。
1 水文序列变异诊断耦合模型
1.1 BG算法
目前,水文序列诊断通常采用传统的统计检验方法,如滑动T检验、滑动F检验、游程检验、秩和检验等,上述方法都有较为严格的假设,即要求序列具有线性和平稳性的特征。而水文序列普遍具有非线性,同时,由于人类活动和自然变异的双重影响,水文序列一般还具有非平稳性。所以,传统的方法对变异水文序列的检测能力有限,检测结果存在一定的偏差。
对序列的假设较为宽松,能准确检测非线性、非平稳的均值变异点。对于一个由N个点构成的时间序列X(t),BG算法进行变异诊断的建模步骤如下[12]:
第1步,从左到右,依次计算每个点左边部分和右边部分的平均值和标准差,分别是: µ1(i)、s1(i)和µ2(i)、s2(i)。
于是,i点的合并偏差sD(i)为:

式中,N1和N2分别为i点左边和右边部分的点数,i=1,2,···,N。
第2步,用T检验的统计值T(i) 量化i点左右两部分均值的差异:

对X(t)中的每一个点重复上述计算过程,得到与X(t)一 一对应的检验统计值序列T(t),T越大,表示该点左右两部分的均值相差越大。
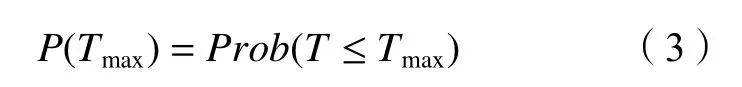
第3步,计算T(t) 中 的最大值Tmax的统计显著性P(Tmax):式中,P(Tmax) 表示在随机过程中取到T值小于等于Tmax的概率。一般情况下P(Tmax)可近似表示为:
第2步,计算任意向量X(i) 与其余向量X(j)之间的相对欧式距离d[X(i),X(j)]。
第3步,设定容许偏差为r,统计每个向量X(i)的d[X(i),X(j)]小 于r的数目,求出该数目与向量总数N−m+1之 比(r)。
第5步,维数m增加1,重复第1~4步,得+1(r)和ϕm+1(r)。
第6步,近似熵的估计值定义为ApEn(m,r)=ϕm(r)−ϕm+1(r)。 显然,ApEn值与m、r的取值有关,Pincus[25]建议r取0 .10σ ~0 .20σ (σ是原始序列的标准偏差)。本文中,取参数m=2 ,最初默认取r=0.15σ。

由蒙特卡洛模拟实验得η=4.19lnN−11.54,δ=0.40,v=N−2,N为时间序列X(t) 总 长。Iv/(v+Tm2ax)(δv,δ)为不完全β函数,其中下标v/(v+ax) 为不完全β函数的上限。
第4步,设定置信度P0和最小分割尺度l0, 对T(t)序列的Tmax进行诊断。若其概率值大于P0,则于该点将X(t)分割成两段均值有一定差异的子序列;否则,不分割。
第5步,对新得到的两个子序列分别重复上述4个步骤,新子序列满足分割条件的同时,如果子序列与其左右相邻的子序列间的均值差异程度均满足上述条件,则继续分割;否则,不分割。如此重复直至所有的子序列都不可分割为止。此外,为保证统计的有效性,当子序列的长度小于等于l0(l0为最小分割尺度)时,不再对其进行分割。通过上述操作,作者将原序列分割为若干个不同均值的子序列,每个分割点即为均值变异点。一般而言,l0≥25,P0∈[0.50,0.95],本文中l0取滑动移除近似熵法处理后的数据样本量的一半,P0取0.95。根据文献[13]可知,l0和P0的取值,对检测结果的影响较小。在解决不同样本量的问题时,通过对两者进行调整,可对序列实现不同尺度的变异检测。
1.2 近似熵
近似熵是一个理想的非线性动力学指数,基于熵理论可以刻画出系统的混乱程度,同时能反映水文序列在模式上的自相似程度。需要的数据点较少,抗噪能力较好,对序列的假设比较宽松,适用于多种信号分析。所以,近似熵在生物、医学、机械故障诊断、通信信号分析等领域都有广泛应用。近似熵方法的主要思想及建模步骤如下[23–24]:
第1步,对时间序列 {u(i),i=1,2,···,N}进行相空间重构,重构维数为m,据此可构造一组维数为m的新向量X(1),X(2),···,X(N−m+1),其中,X(i)=(u(i),u(i+1),···,u(i+m−1)),i=1,2,···,N−m+1。
1.3 数据滑动技术
数据滑动技术用于剔除水文序列的随机性,其建模步骤如下:第1步,选择滑动移除数据的窗口长度L;第2步,从待分析时间序列的第i(i=1,2,···,N−L+1,N为时间序列的总记录个数)个数据开始连续移除L个数据,再将剩余N−L个数据直接连在一起得到一个新的时间序列;第3步,利用近似熵方法计算新序列的近似熵值;最后,固定滑动步长L不断重复第2步和第3步直至序列结束,即可得到一个随窗口移动而变化的近似熵序列。
1.4 耦合模型
本文构建一种水文变异诊断耦合模型,建模步骤如下:首先,以近似熵刻画水文序列各点的动力学状态,基于数据滑动技术充分利用水文序列的各点信息,得到随着滑动窗口移动而变化的近似熵值。其次,运用BG算法依次对各点进行一分为二的迭代计算、对比。再次,根据提前设定的置信度检测出所有的变异点,以变异点对近似熵序列进行动力学状态的划分,由此揭示水文序列的内在演变规律。本文提出的耦合模型,具有客观性、稳定性和直观性。对一个由N个点组成的水文序列X(t)来说,耦合模型建模步骤如下:
第1步,利用近似熵和数据滑动技术对X(t)进行处理,从而得到一个待检测的近似熵序列X′(t),初步得到了刻画水文要素内在演变机理的量化值。
第2步,对近似熵序列各点逐一进行一分为二的检测分析,从而得到近似熵序列各点T检验统计值序列和置信概率序列,统计值和置信概率的计算参见式(2)和(4)。
第3步,根据第2步得到的分割置信概率序列对原序列X′(t)进行水文动力学状态划分;若其置信概率大于原先设定的P0,则以此为不同状态的分割点,也即变异点;反之,则不进行分割。
第4步,画出X′(t)的序列图和不同动力学状态划分结果,初步判断近似熵值骤升或骤降的变异点位置,再根据置信概率计算结果进一步确定变异点的位置和数目。
综上,水文变异诊断耦合模型的算法流程和建模步骤如图1所示。

图1 耦合模型的算法流程和建模步骤Fig. 1 Algorithm flow and modeling steps of the coupling model
2 模拟实验
2.1 耦合模型在线性时间序列中的性能测试
2.1.1 线性时间序列的构建
为比较耦合模型和仅使用滑动移除近似熵的检测结果的优劣,本文沿用的线性理想时间序列是在王启光等[26]构造的方程(5)基础上,修改一些参数所得的方程(6),以检验耦合模型的变异诊断结果。需要说明的是,对方程(5)修改的目的是降低演化曲线的周期数和均值差异,使之存在弱性的动力学结构变异[26]。

图2(a)和(b)分别是式(5)和(6)所构造的理想时间序列IS1和IS2的演化,由式(5)和(6)可知,IS1和IS2在t=1 001处都发生了动力学结构变异,其控制方程由简单的正弦函数变异为正弦函数和余弦函数所组成的新方程。
通过观察图2,能直观感受到IS1和IS2的不同,IS1时间序列代表的水文系统在1~2 000样本点内包含更多的周期数,在t=1000变异点前后,表现出更复杂的变化;IS2则反之。因此IS1和IS2分别代表了强趋势动力学结构变异和弱趋势动力学结构变异。

图2 线性时间序列的演化Fig. 2 Evolution curves of linear time series
2.1.2 耦合模型对强趋势动力学结构变异(IS1)的性能测试
令r=0.15σ,L=10、20、50、100情况下,利用耦合模型对IS1序列进行变异诊断,结果如图3所示。
由图3可知,不同滑动步长情形下,耦合模型均得到IS1序列在t=1000左右发生动力学结构变异,与滑动移除近似熵的变异诊断结果一致。

图3 不同的L下使用耦合模型的IS1检测结果Fig. 3 Results of coupling model detection for IS1 under different L
耦合模型变异诊断的置信曲线如图4所示。
图4表明不同滑动步长下耦合模型的变异置信度均超过了95%。因此,对于强趋势动力学结构变异,耦合模型不仅能准确给出变异点的位置,而且能给出变异点的置信水平。而滑动移除近似熵方法只能通过直观观察近似熵图像得到变异点的大概位置,具有很大的主观性。

图4 图3中对应4幅图位于t =1 000附近的变异点置信曲线Fig. 4 Confidence images of variation points near t =1 000 for the corresponding four images in Fig. 3
2.1.3 耦合模型对弱趋势动力学结构变异(IS2)的性能测试
IS1所刻画的动力学结构变异是一种理想的强趋势变异;当发生的动力学结构变异较弱时,如式(6)所构造的IS2(图2(b)),仅使用滑动移除近似熵方法无法对变异情况进行主观判断。
1)滑动移除近似熵的诊断结果
利用滑动移除近似熵方法对IS2进行变异诊断,结果如图5所示。由图5可以看出,弱变异情况下,L的取值对检测得到的ApEn曲线形状的影响很大,说明滑动移除近似熵方法在弱趋势变异时对L的取值很敏感。观察图5,得到以下判断结果:L=10时,能观察到在t=1 000附近有较为明显的变异;L=20时,无法观察到明显的变异;L=50时,在t=1 000观察到变异,同时在t=1 000~1 400之间也存在一个类似的变异,无法给出确定的变异点位置和数目;L=100时,观察不到变异。综上,当滑动窗口长度L≥20时,滑动移除近似熵方法无法确定变异点的数目和位置。
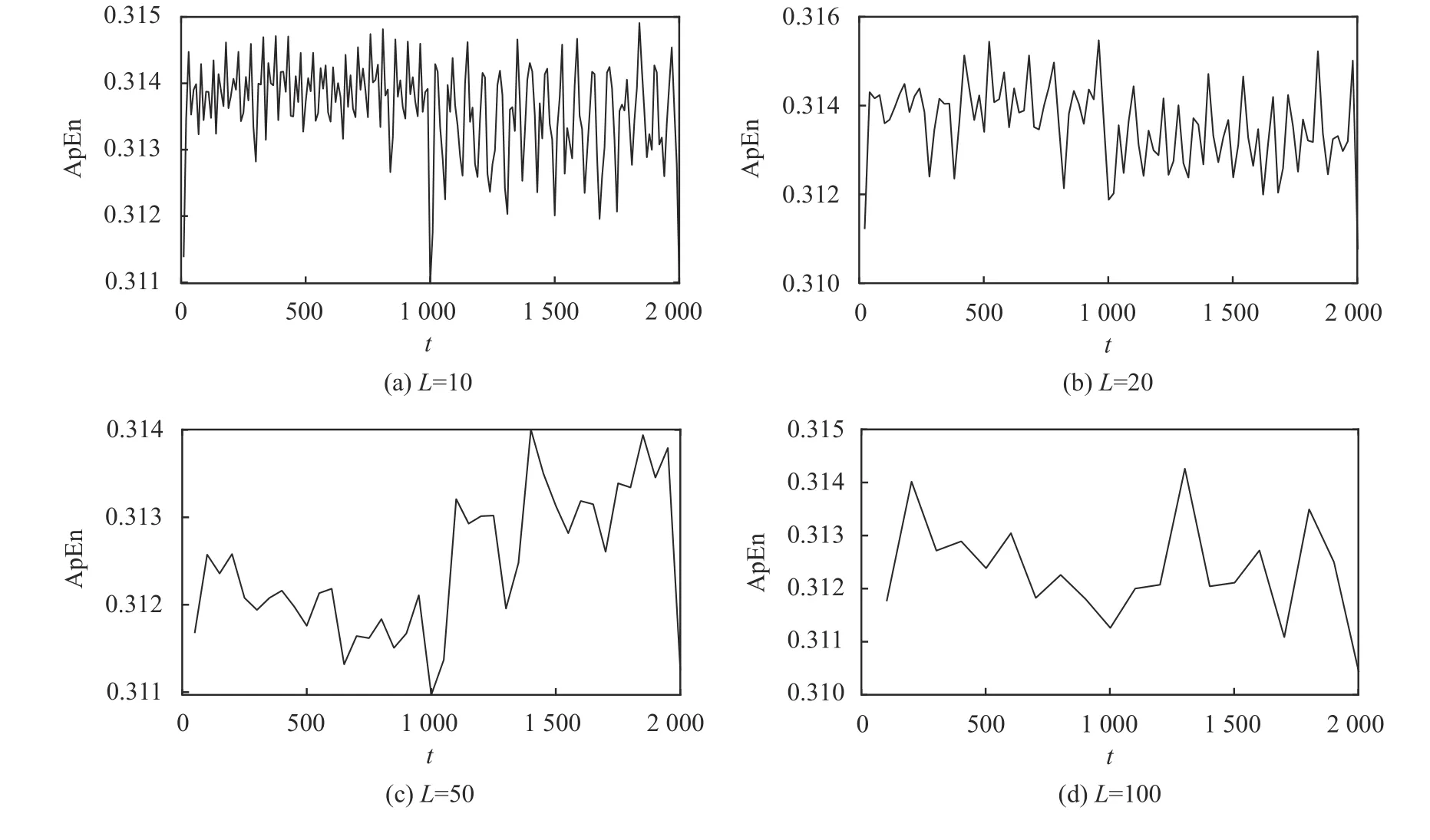
图5 不同L设置下的滑动移除近似熵法的IS2变异诊断结果Fig. 5 Results of moving cut approximate entropy for IS2 under different L
2)耦合模型诊断结果
在给出耦合模型结果之前,先介绍变异区间的概念。变异区间由算法侦测到的变异点所决定。当对N=2 000样本量的序列进行诊断时,如果设滑动窗口L=l,检测到的变异点为Y,那么变异区间为[Y−l+1,Y]。 当设定了滑动窗口的数值l后,就会把该值之前(包括该值在内)的l个数值移除;然后,对剩余序列进行分析,得到一个近似熵值;接着,会从2l开始往前取到l+1, 由此往复直至取完nl=N。因此,变异区间的含义是:某次移除了l个数值,则剩余序列得到的近似熵值发生了异常,认为变异点就出现在这l个数值中。
利用耦合模型对IS2进行变异诊断,结果如图6所示。

图6 不同L设置下的耦合模型IS2变异诊断结果Fig. 6 Result of the the coupled model for IS2 under different values of L
由图6可以看出:L=10时,得出的变异点为t= 990和1 020,均值曲线在该点附近呈凹谷状,t=990处均值减弱,t=1 020处均值变异增强,在形式上虽不如阶梯状直观,但大概能找出预先设置的变异点位置;L=20时,得出变异点为t=980,t=[961,980]为变异区间,由于构造的方程为线性的,因此在右侧边界附近检测到一个虚假变异点;L=50时,变异点为t=1 010,t=[961,1 010]为变异区间,另外检测到了一个虚假变异点t=600;L=100时,变异点为t=1 900,t=[1 801,1 900]为变异区间。综合比较滑动移除近似熵方法的结果和耦合模型的诊断结果如表1所示。
从表1看出:大部分情形下滑动移除近似熵方法不能检测出实验设置的变异点,且即使可检测到,也只能基于观察给出模糊的位置;而耦合模型可以检测出变异点及变异区间;虽然耦合模型的精度在某些滑动步长下存在一定的偏差,但都在可接受范围内,如L=20时有一个多余变异点,是由式(5)的线性特点影响的,但并不影响应用;在L=50情况下有一个虚假变异点,这说明耦合模型对L是敏感的,需要进一步探索出参数的合理取值以提高模型性能。综上,在弱趋势变异下,样本量为2 000时,耦合模型取L=20、r=0.15σ时可以得到良好的结果。

表1 耦合模型与仅使用滑动移除近似熵方法的检测效果对比Tab. 1 Comparison of the detection effects of the coupling model and the sliding removal approximate entropy method only
通过上述实验,关于耦合模型可得出以下结论:对强趋势和弱趋势变异均有较好的检测表现。对动力学结构弱趋势变异,在特定L情况下具有良好性能,但具体L应该如何取值使耦合模型的性能更好,仅凭目前的实验结果还无从得知,需要在不同样本量下对r和L的取值进一步研究才能提高模型的检测精度。
2.2 弱趋势变异情况下耦合模型对r 、L的取值评价
为进一步提高模型的精度,对模型中的参数进行敏感性分析。耦合模型精度主要受3个参数的影响,即样本量N、滑动窗口长度L和容许偏差r。
2.2.1r、L对近似熵序列的影响
r的影响:
1)取较大值,可以接受时间序列数据点向近似熵值转化过程中更大的偏差,近似熵曲线波动振幅增强,趋势变化因受到各点偏差的影响而被掩盖;
2)取较小值,可以强化精度的要求,近似熵曲线的波动振幅会减弱,趋势变化对于耦合模型会更清晰。
图7能进一步说明以下规律:在样本量N都为2 000,且L=20 时,容许偏差r从0.15σ 到0.10σ变化,近似熵序列波动振幅减弱,变异点附近的变化趋势更明显;从0.15σ到 0.60σ是r取值变大的过程,近似熵序列波动振幅增大明显,在变异点附近的趋势直接被掩盖掉了。

图7 N=2 000,L=20时取不同的r值的近似熵序列Fig. 7 Sequence of approximate entropy with different values of r when N=2 000 and L=20
L的影响:
由图3可知:L越大,近似熵序列波动性越小,变化趋势越明显;L越小,则反之。在同一样本量N下,L和r对诊断结果的影响并不是相互独立的,而是交织在一起的,因此,需要构建搜索模型,通过依次生成(r,L)数对,在2 000样本量下探索出耦合模型具有良好性能时的(r,L)取值。
2.2.2 搜索模型
确立一个搜索模型对 (r,L)进行搜索,其核心方法是遍历算法,由于要筛选出符合精度的取值,先设定两个指标:检测误差Γ (即L与 样本量N之比的百分数)和误差度Ψ(即耦合模型得出的变异区间的上限b或 下限a距 离理想变异点Y的最小值z与 样本量N之比的百分数)。
其中,z=min{|b−t|,|a−t|},a=Y−L+1,b=Y。
在此基础上,定义权重误差ξ,ξ= 0.5Γ+0.5Ψ,为检测误差和误差度的加权组合,权重均取0.5,如图8所示。

图8 权重误差阐释Fig. 8 Weight error illustration

结合上述权重误差公式与图8,权重的选取基于以下考虑:1)在样本量固定时,检测误差Γ来源于滑动窗口L大小,控制变异区间,以防止过大。若区间过大,即变异点Y被变异区间包括,并不能仅以Y被检测入变异区间为评判方法好坏的标准。2)为了使变异点Y不被包含在变异区间,若Y处于变异区间中,则Ψ值恒为0,误差主要来自Γ ;若Y不在变异区间中,则产生了两部分误差,其中,一部分是Γ,另一部分通过误差度Ψ进行量化。综上,视两部分误差影响处于均势的地位,权重各取0.5。可以在不同应用场景下对权重进行调整,建议遵守权重相加为1,并且每一个权重应不低于0.3。
对于搜索模型的搜索范围,当N取2 000时,r应该在 (0,0.50σ]范 围内遍历寻优,步长为0.05σ。因为过高的r能使近似熵曲线整体趋势放大,进而抹除了变异点处的变化趋势,加大了耦合模型的检测难度。L相 对于N不能过大或过小,认定L最大的偏差为2%,即最大取值为 2%N。在 [ 1,2%N]范 围内遍历能整除N的数值是可行的,因此L分别取5、10、20、25和40。
2.2.3 搜索 (r,L)使 权重误差 ξ最小
通过依次生成 (r,L)数对,在2 000样本量下探索出最优的参数对(r,L),如表2和3所示。由表2和3可以看出,在L=5、10且r在 ( 0,0.50σ]取值时,耦合模型的检测结果的精度比其余 (r,L)组合更高,且有聚集趋势。

表2 N=2 000,L=5下各r取值下检测到的结果分析Tab. 2 Analysis of the detected results under each r value when N=2 000 and L=5
进一步观察表2可以看出,当L=5时,r∈{0.05σ,0.10σ,0.30σ,0.40σ,0.45σ}有较好的检测结果,都仅离理想变异点t=1001一个样本点之差,且权重误差仅有0.15%。由表3可知,当L=10时,r∈{0.35σ,0.40σ,0.45σ,0.50σ}有较好的检测结果,检测到变异区间中包括了理想变异点,权重误差为0.50%,比0.15%大。结合刘群群等[27]对非线性动力学指标近似熵在气候突变检测中模拟应用的研究,及冯文宏等[28]使用近似熵对泾河径流量序列进行变异诊断,说明耦合模型对长序列变异诊断具有良好的效果。

表3 N=2 000,L=10下各r取值下检测到的结果分析Tab. 3 Analysis of detected results under each r value when N=2 000 and L=10
因此,在N=2000,L=5及r∈{0.05σ,0.10σ,0.30σ,0.40σ,0.45σ}的参数设置下,耦合模型对于弱趋势动力学结构变异检测具有较好的性能。
2.3 弱趋势变异情况下耦合模型对于不同样本量下r 、L评价试验
为了对模型的实用价值进行更深入的研究,接下来改变样本量,进行之前的r、L搜索实验,结果如表4所示。

表4 对IS2进行不同样本量水平下的(r ,L)搜索实验所得结果分析Tab. 4 Analysis of the results for IS2 with different sample sizes ( r,L)
由表4可知:当样本量较高(如N=4 000~8 000)时,权重误差均较小,耦合模型检测到的变异区间中包括设置的理想变异点,且样本量越大,检测越精确;在样本量N=60~3 000时,检测的变异区间虽然无法包含真实变异点,但与真实变异点较接近,可以接受。
3 应用实例
3.1 窟野河温家川径流变异检测
选取窟野河温家川站1956—2019年的年径流量序列作为研究对象,开展耦合模型的应用研究。根据表4给出的耦合模型参数取值结果,当样本量为60左右时,取r=0.50σ,L=1。耦合模型的变异诊断结果如图9所示。由图9可知,近似熵序列被分成了3个不同均值的时段,代表3种不同的动力学结构的稳定演变状态,因此窟野河年径流量序列在1983年和1996年发生了变异,且变异发生的概率接近100%。

图9 使用耦合模型检测窟野河温家川1956—2019年年径流量分析Fig. 9 Annual runoff analysis of 1956—2019 in Wenjiachuan,Kuye River by using the coupling model
3.2 变异成因分析
相关研究表明,由于全球气候变暖和大规模的人类活动导致了水循环在时间和空间上的重新分配,使水循环要素如降水、蒸散发、径流等发生显著变化[1]。查阅窟野河温家川1956—2019年的相关人类活动和气候变化文献[29–32],可以得出以下分析结果:
1)1956—1978年间,降水是影响径流的最主要因素。20世纪70年代末,窟野河流域大规模实行水土保持措施,包括修筑堤坝、植树造林、梯田建设等,这些人类活动对径流量的减少起到直接作用。20世纪80年代初期,流域内多处中大规模的煤矿资源开采开工,加速了水土流失的进程[29–31]。自1979年以来,人类活动对径流的影响的占比越来越大,且呈增加的趋势,除此之外,1979—1995年降雨量减少直接导致径流量的减少,因此在人类活动和自然因素的影响下,径流序列在1983年发生了变异,符合实际情况。
2)20世纪90年代以来,人类活动已经成为影响径流的主导因素,煤炭的开采量于1996年开始出现大幅度的增加[32]。这显然对径流有着新一轮的影响,因此,径流序列在1996年发生了变异,也符合实际情况。
4 结 论
本文建立了一种基于BG算法和近似熵的水文变异诊断耦合模型。主要建模步骤如下:首先,以近似熵刻画水文序列各点的动力学状态,基于数据滑动技术充分得到随着滑动窗口移动而变化的近似熵序列;其次,运用BG算法依次对各点进行一分为二的迭代计算、对比,得到每个点的检验统计值和置信概率;最后,根据置信概率结果判断是否需要对近似熵序列进行分割,因此,确定变异点的数目和位置。通过大量模拟实验,证明耦合模型具有如下潜力:
1)对强趋势和弱趋势情况均有较好的检测表现。对动力学结构弱趋势变异,在特定L情况下具有良好的性能。
2)在N=2000,L=5 及r∈{0.05σ,0.10σ,0.30σ,0.40σ,0.45σ}的参数设置下,耦合模型对于弱趋势动力学结构变异检测具有较好的性能,检测误差较小。
3)当在样本量较高(如N=4 000~8 000)时,权重误差均较小,耦合模型检测到的变异区间中包括设置的理想变异点,且样本量越大,检测越精确;在样本量N=60~3 000时,检测的变异区间虽然无法包含真实变异点,但与真实变异点较接近,可以接受。
利用耦合模型对窟野河温家川站1956—2019年的年径流量序列进行变异诊断研究,结果表明窟野河年径流序列在1983年和1996年发生了变异,与实际情况基本吻合。
本文提出的耦合模型对于大样本具有良好的性能,但是样本量较小(小于等于50)时,模型的效果不是很理想,这一情况在滑动移除近似熵方法中更为严重[33]。而中国很多流域缺乏足够的水文观测数据,缺资料地区的水文变异诊断技术仍需进一步探索研究。

