科学基金项目成果后评价体系构建及应用
张仲位 朱洋 张彦明 张其斌 祁楌捷
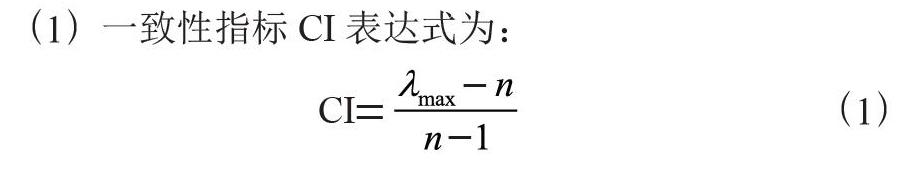
摘要:文章提出一种采用层次分析法对已受理项目进行评审的评审体系,通过研究分析不同学科科学基金项目后绩效评估所涉及的评价指标,选择能够反映科学基金项目特点的共性指标并对其中的定量指标分别设定权重,从数量、质量、效率三方面得出项目综合评分,然后结合关键定性指标,建立了一套定量与定性相结合的科学、系统、实用的基金项目后评价指标体系以及评价意见的反馈机制,最后通过实际数据验证了该评价体系的合理性与有效性。
关键词:科学基金项目;评价体系;决策分析;科研管理;层次分析法
中图分类号:N32 文献标识码:A 文章编号:2096-4706(2021)07-0101-06
Construction and Application of Post-Evaluation System of
Science Foundation Project Achievements
ZHANG Zhongwei1,ZHU Yang1,ZHANG Yanming2,ZHANG Qibin3,4,QI Yanjie5
(1.School of Mathematics and Physics,Lanzhou Jiaotong University,Lanzhou 730070,China;2.Weiyuan County Water Authority,Dingxi 748200,China;3.Gansu Computing Center,Lanzhou 730070,China;4.Gansu Key Laboratory of Cloud Computing,Lanzhou 730070,China;5.Gansu Rongzeyuan Data Technology Co. Ltd.,Lanzhou 730070,China)
Abstract:This paper proposes an evaluation system of accepted projects by using analytic hierarchy process. By studying and analyzing the evaluation indexes involved in the post-performance evaluation of science foundation project in different disciplines,the common indexes that can reflect the characteristics of science foundation projects are selected,and the weights of the quantitative indexes are set respectively. The comprehensive scores of projects are obtained from the three aspects of quantity,quality and efficiency. Then combined with key qualitative indicators,a set of quantitative and qualitative combined science,system,practical foundation project evaluation index system,and feedback mechanism for evaluation opinion. Finally,the rationality and effectiveness of the evaluation system are verified by the actual data.
Keywords:science foundation project;evaluation system;decision analysis;scientific research management;analytic hierarchy process
收稿日期:2021-03-09
基金项目:甘肃省自然科学基金项目(17JR5 RA014);甘肃省科技计划资助项目(20YF3GA0 13);甘肃省科技型中小企业技术创新基金项目(20 CX9JA128)
0 引 言
自然科学基金是各省市设立的用来鼓励和支持地方自然科学创新与发展的重要举措,目的在于培养科学技术人才,发现并发展前沿科学研究,增强各地基础性研究的自主创新能力[1]。省市各个地方对自然科学基金研究的课题立题、中期检查、结题验收都有相应管理办法,但对结题验收后项目优劣程度的定量评价缺乏系统性,或是采用的定量评价体系过于简单笼统,而且细化程度不够[2-6]。
近年来,随着甘肃省科学基金项目的发展,其管理措施也逐步完善。由于基金項目的后期管理工作是管理措施中较为薄弱的环节,它不仅对项目完成情况的评估有影响,也不利于新事物的发现,且浪费了数据资源。因此,为适应日益发展的基金事业,我们联合甘肃省科技厅,从已有的项目数据中分析得出新的规律与价值,建立甘肃省已结题项目的后评价体系,从而提升项目基金的资助质量与后期管理,提高使用效益。基金项目后评估是通过全面收集已结题项目的成果检索率、引用率、专著出版、专利申请、人才培养、获奖情况、成果转化等一系列指标信息,利用层次分析法给予不同的指标权重,对项目的价值以及创新水平做出客观评价,为甘肃省科技厅基金管理机构的项目后期管理提供依据。此外,通过该评估体系发掘前景较好、有发展潜力的研究领域,为基金管理机构的资金分配提供决策依据,增强省科技厅管理人员在项目基金分配中的判断力。
1 基金项目评价模型建立
1.1 层次分析法简介
层次分析法于1970年初由美国运筹学家萨蒂教授提出,是一种定性定量相结合的建模分析方法,用来解决无结构决策问题。层次分析法(Analytic Hierarchy Process,AHP)[8]是对人们的主观评价进行形式化表达以及客观描述过程,得到权重之后,为了克服成对比较的缺点必须进行一致性检验。层次分析法的关键是对决策者主观经验判断进行量化表达,使得决策者在决策时候有据可依,避免过于依赖个人的主观判断,在目标结构复杂、所需数据较多的情况下更加实用[9]。由于在复杂问题决策中AHP有较强的实际应用性,故其应用范围广泛,涉及经济规划与管理、能源政策与分配、军事指挥、交通运输、农业、教育教学、人才培养、医疗建设等领域。
AHP的基本思想类似于思考和识别复杂决策问题的过程。将研究对象划分为不同的组成部分,按照各组成部分的隶属关系由高到低排序,构建层次结构。通过比较同一层的要素利用数学方法确定各层要素的权重。
1.2 层次分析法的具体步骤
应用AHP计算指标权重系数就必须将指标体系分层创建,因为它是计算指标权重系数的基础,通过指标之间的成对比较来判斷系统中各指标的好坏,并根据评价结果综合计算各指标的权重系数。下文对具体步骤进行介绍。
1.2.1 建立递阶层次结构
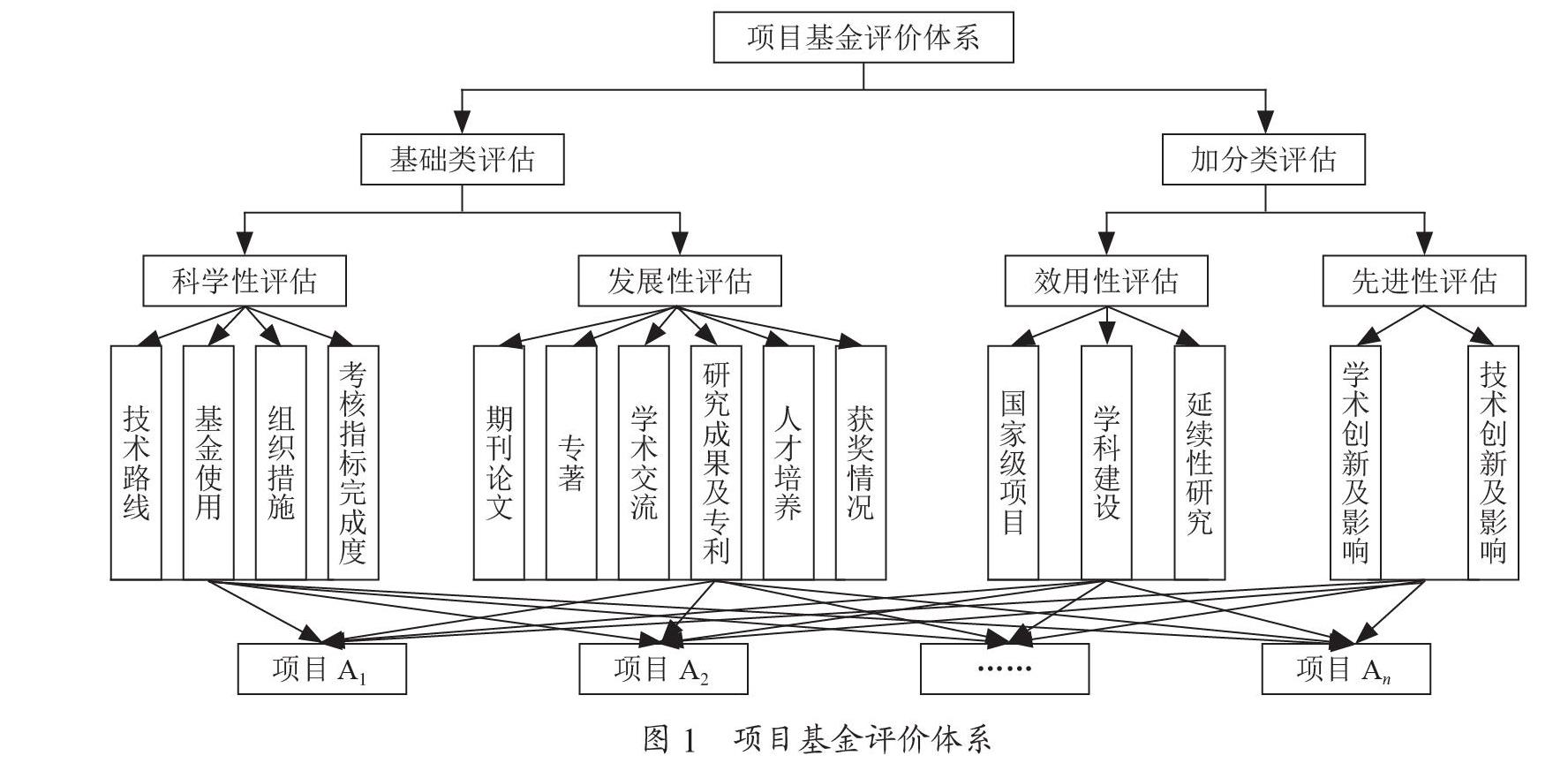
将烦琐问题中的各种因素分解为相互关联、有序的层次,使之组织有序,层次分明,构建清晰的层次分析结构模型。评价体系形式如图1所示。
1.2.2 构造判断矩阵
矩阵用于表示相同等级中各指标相对重要程度判断,由多位专家进行判断。心理学家研表明“一个人区分信息水平能力的极限为7±2”,为了解决直接评价指标的模糊性及不确定性,AHP法运用了九分位的相对重要比例标度来衡量相对指标,构成一个判断矩阵B。矩阵中的每个元素bij表示水平索引相对于每列索引的重要性的成对比率[10-13]。如表1所示。
依据判断矩阵B中两个指标的比较特征,显然有bij>0,bii=1,bij=,i=1,2,3,…,n。因此,判断矩阵B是否为一个正交矩阵时,只需作次比较即可。这里需要强调的是,如果认为后一个指标比前一个指标重要,则用对应值的倒数来表示其重要性。
1.2.3 对各指标权重系数进行计算
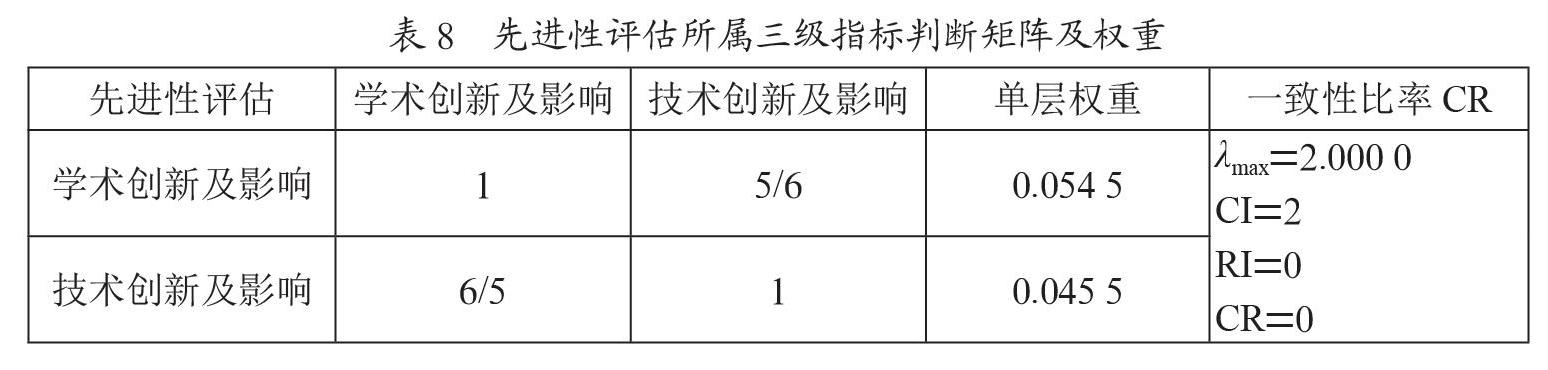
单级层次排序,是指本级各因素对上一级某一因素的重要性排序。判断矩阵是AHP法的信息来源基础,用排序方法得到矩阵排序后,计算出各级指标权重系数,如表2到8所示,一致性指标CR均小于0.1,满足判断矩阵的一致性检验。
1.2.4 判断矩阵的一致性检验
对其他计算指标权重的方法进行比对后发现,层次分析法优势在于一致性检验后可以与专家思维保持基本相同。这种与专家思维保持一致我们称为判断一致性,指多个指标相互比较时也可以相互协调互不干扰。例如,使用三个指标(令它们分别为a、b、c)进行两两比较。当a比b略微重要,b比c稍微重要时,存在c比a稍微重要的评价,相互矛盾,此时称专家思想非不一致性。这种不一致的矛盾在多层次判断中极易出现,仅仅是不一致的程度不同[14]。
将多位专家得到的最终判断矩阵采用几何平均法进行综合平均,得到最终的指标评价判断矩阵。判断矩阵一致性的步骤为:
(1)一致性指标CI表达式为:
(1)
其中λmax为判断矩阵的最大特征值,可采用下文所述的方法计算。定义:
(2)
(2)式可以作为判断矩阵的最大特征值对应的特征向量:
(3)
(3)式可以近似看作判断矩阵的最大特征值。
(2)一致性指标RI。如表9所示。
(3)计算一致性比率CR,表达式为:
CR=
当CR≤0.1时,判断矩阵一致;当CR>0.1时,则认为判断矩阵并没有达到要求,需要重新分析赋值并进行修正,直至检验通过。由步骤三中的数据计算可知,一致性比率CR都小于0.1,接受判断矩阵的一致性。
1.2.5 组合权重计算
指标权重是一级接着一级去计算的,设有一个由目标层A、准则层C、方案层P组成的分层模型(增加更多的分层模型,计算方法相同),目标层A对准则层C的相对权重W为:
W=(w1,w2,…,wk)T
式中W为各个指标的权重系数值。
准则层C的各准则ci(i=1,2,3,…,k)(k为准则数)对方案层P中的所有n个方案的相对权重为:
Wi=(w1i,w2i,…,wni)
通过W与Wi(Wi=1,2,3,…,k)计算各方案目标的相对权重。对于该基金项目评价体系的组合权重计算如表10所示。
1.2.6 权重指标分析
由表10可以得到各层指标的单层权重和总权重,对于该评价体系经过上述分析,认为一个基金项目的评审主要在于基础类评估,占比70%,其次是二层指标中的效用性评估,将上表中的15个第三层指标用1~15来表示,由图2可以看出第三层指标对于目标层的相对权重大小,权重相对较大的是研究成果及专利,占比13.13%,说明关键指标占权重的比例较大,关键指标在评价体系中可以发挥作用。权重较大的指标基本上覆盖了对基金项目进行有效性评价的一些很重要的方面,然后由权重较小的指标对基金项目有效性评价做一些有益的补充。
2 实际应用
为了检验该评价体系的合理性,我们从甘肃省科学技术厅获得了30个已经完结的基金项目。根据该评价体系对这30个完结项目的优良程度进行评比,结果如表11所示。
如图3所示,排在前三位的分别是加速器电源技术的研究、法医物证技术与研究、甘肃大宗药材当归、甘草膜分离提取技术及应用研究,相对权重分别为0.049 2、0.046 5、0.044 5,与实际评比相符。
3 結果与讨论
通过对这30个完结项目的权重排名可知,依据该评价体系得到的项目权重排名和专家评比结果基本一致,因此在科学基金项目评审上可以借鉴该评价体系,根据每一级的指标权重来确立评价主线,为科研项目的评审工作减压,科研人员也可以根据该评价体系对科研经费的投入进行合理分配,减少科研项目投资风险,提升研究经费的使用效率。
利用层次分析法确定项目评价指标权重的优点是可以有效避免权重确定的随意性和模糊性等缺点,有助于提高评价的客观性。本文所讨论的方法是基于从粗到细、从散到集中的选择方案的思想,符合人们的惯性思维,采用特征值法计算权重,后续可以考虑多种方法加权计算最终权重,保证模型的稳健性。此外,建立判断矩阵是确定评价标准权重系数的关键,判断矩阵中必须采用科学合理的数据,不能依靠个人主观判断,在实际应用中,它是综合考虑统计数据、专家建议和决策者知识水平得出的。
4 结 论
本文针对基础研究和应用研究侧重点不同导致的评价指标多样化,量化难度大等问题,采用大数据采集与分析技术对我省已结题科学基金项目在结题后一定时期内所产生的绩效信息进行收集和分析,在自然科学基金项目评价指标体系中选择了一些能够反映基础研究与应用研究基金项目特点的共性指标,并结合层次分析法构建了定量与定性相结合的通用基金项目后评价指标体系,最终形成评价报告。通过真实数据的检验,该评价体系的评比结果与专家意见基本一致且效果显著,效率提高,在实际应用中,可根据具体情况与用途对该评价体系的指标进行适当调整,以满足实际需要。
参考文献:
[1] 李雄诒,李新杰.我国省级自然科学基金管理体制研究 [J].科学学与科学技术管理,2011,32(3):16-20.
[2] 刘长颖.层次分析法与高校科研项目评估指标权重的确定 [J].辽宁师范大学学报(自然科学版),2011,34(1):30-33.
[3] 林建衡.层次分析法在高校科研项目评估中的应用 [J].技术与创新管理,2004(2):39-41.
[4] 王其冬,武佩珍,程建刚,等.层次分析法在国家自然科学基金项目评审中的应用 [J].系统工程理论与实践,2001(7):119-123.
[5] 臧玉强.层次分析法在科技成果综合评价中的应用 [J].济宁师专学报,1999(6):13-14.
[6] 王英凯.基于德尔菲法和层次分析法原理的科研项目评价模型 [J].山西财经大学学报,2001(S2):148-149.
[7] 魏江,勾丽,周泯非.基础研究绩效的评价指标分析 [J].南京理工大学学报(社会科学版),2008,21(2):64-69.
[8] SAATY T L,KEARNS K P. Analytical Planning [M].Elsevier,1985.
[9] DETURCK D M. The approach to consistency in the analytic hierarchy process [J].Mathematical Modelling,1987,9(3-5):345-352.
[10] 曹亚平.层次分析法在建筑施工现场安全管理中的应用 [J].山西建筑,2021,47(1):190-192.
[11] 徐恒,时晨希,徐艳芳,等.基于层次分析法开展医院大型医疗设备用能评价及对策探讨 [J].医疗卫生装备 2021,42(2):78-81.
[12] 吴翼虎.基于层次分析法对山区高速公路路线设计方案评价模型的构建与研究 [J].公路,2021,66(4):56-61.
[13] 李秀峰,祝军.共青团“青年之家”实体平台的评估指标体系研究——基于德尔菲法和层次分析法的应用 [J].中国青年社会科学,2021,40(2):28-39.
[14] 刘新宪,朱道立.选择与判断——AHP(层次分析法)决策 [M].上海:上海科学普及出版社,1990.
作者简介:张仲位(1996—),男,汉族,甘肃庆阳人,硕士在读,研究方向:时空数据挖掘与人工智能算法;通讯作者:张其斌(1978—),男,回族,甘肃兰州人,甘肃省计算中心研究员,本科,研究方向:计算机应用。

