复杂曲线轮廓度全域评定方法研究

陈宇航，邹春龙，王生怀，王金刚，张伟

（1.湖北汽车工业学院，湖北 十堰442002；2.东风活塞轴瓦有限公司，湖北 十堰442002）

在先进精密制造领域中，能否对零件三维型线和复杂空间曲面进行高效率、高精度的检测和误差评定是影响产品质量和寿命［1-2］的因素。针对曲线轮廓度的评定，学者侧重于平面曲线领域的研究。文献［3］基于最小条件法，采用模拟实际量具测量过程的方法来评定平面线轮廓度误差；文献［4］采用最小二乘法，结合样条插值函数与优化技术来处理数据，从而实现空间平面曲线轮廓度误差的评定；文献［5］采用了特定的一维搜索法，实现自由曲线轮廓度误差评定中的坐标系自适应调整；文献［6］提出用逐次逼近思想来评定平面自由曲线的轮廓度误差的方法。文献［7］提出的正交最小二乘法将曲线轮廓度误差的最小二乘评定从基于代数距离转变为基于法向距离，提高了误差评定的准确性；文献［8］采用非均匀有理B样条（NURBS）插值与遗传算法相结合的方法来评定复杂平面曲线轮廓度。曲线轮廓度误差评定的核心是确定测量点到理想曲线的最短距离，如何快速准确的求解测量点到理想曲线的最短距离成为研究重点。文献［9］提出了计算点到空间参数曲线最小距离的3种算法。文献［10］提出用非均匀有理B样条表示自由曲线，应用改进遗传算法重建自由曲线，基于拟随机Halton序列产生均匀数据参数值计算点到重建自由曲线最短距离。针对复杂曲线轮廓度误差的评定，在空间曲线函数关系式无法表达的情况下，学者一般根据实测离散点拟合曲线函数，测量实测点到拟合曲线函数的距离来评定线轮廓度。

由于复杂空间三维曲线的特殊性，曲线的轮廓难以用函数关系式表征。文中针对复杂三维空间曲线轮廓度评定，提出一种构建包络圆方程来评定复杂全域线轮廓度的方法。首先针对于三维空间曲线轮廓的复杂性，提取理论轮廓曲线与实际轮廓曲线，根据被测轮廓线的特点，分别将理论轮廓曲线与实际轮廓曲线转化为点坐标，并以理论轮廓点坐标建立包络区域函数，最后通过包络组圆函数来确定线轮廓误差。

1 三维轮廓评定复杂度

线轮廓度公差带是指包络一系列直径为公差值d的圆的两包络线之间的区域。诸圆的圆心位于具有理论正确几何形状线上，图1为线轮廓度公差定义示意图。

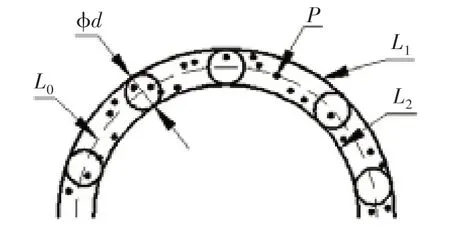
图1 线轮廓度公差定义示意图

国标定义轮廓度曲线是在二维平面内进行评定的，未给出三维曲线轮廓度的评定方法。空间中三维曲线由空间点的位置决定，受x、y、z方向的影响，难以直接评定。根据被检测零件的形状与功能，分析影响空间曲线轮廓度误差影响最大的方向，最终确定线轮廓度。图2为被检测零件模型及型线提取示意图。线轮廓度误差分为x、y、z轴3个方向，根据零件特性，分析得出y轴是影响线轮廓度的主要方向。

图2 零件模型及被测型线提取示意图

2 三维轮廓采样与维度处理

2.1 三维轮廓提取

被检测零件内部的曲面光滑且连续。为准确描述曲线轮廓，按照型线位置选取圆柱函数：

图3为圆柱函数示意图，获取被测轮廓型线。空间点由直角坐标系到柱坐标变换如下：

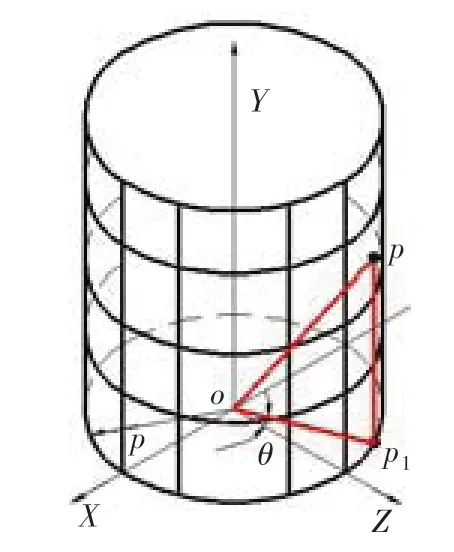
图3 圆柱函数示意图

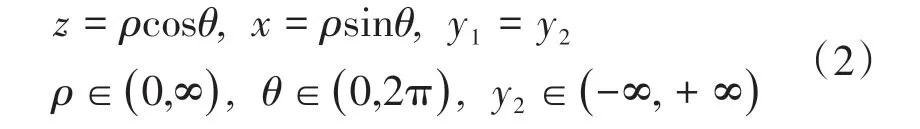
式中：ρ为截面圆柱的半径；θ为oP1与z轴的夹角，oP1为曲线轮廓线上点P在xz平面的投影P1与o点的连线。当ρ取某定值时，被测空间轮廓线函数：

式中：u为型线上的点在z轴方向的分量；v为型线上的点在x轴方向的分量；w为型线上的点在y轴方向的分量。

2.2 维度处理

空间曲线在2π范围内，经过坐标变换将空间点（u,v,w）转换为二维曲线：

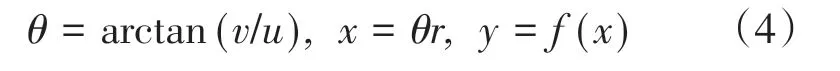
式中：θ∈(-π,π)。将二维曲线的x坐标进行n等分，得到点云数据，用矩阵Π表示：

式中：pi为型线上第i个离散点序号值，i∈［1,n］；yi为型线上第i个离散点的在y轴上的分量。

3 误差评定方法

3.1 采样点的归一处理

受检测环节限制和噪声点混杂，采样数据的坐标与理论轮廓上对应点的坐标不完全匹配，造成评估过程中采样数据位错。空间采样数据与理论轮廓点，经过维度处理后，进行归一化处理，即保证评估点与检测点之间相互对应。空间实测点与理论轮廓的配对，按照维度处理原则，实测点矩阵Γ为

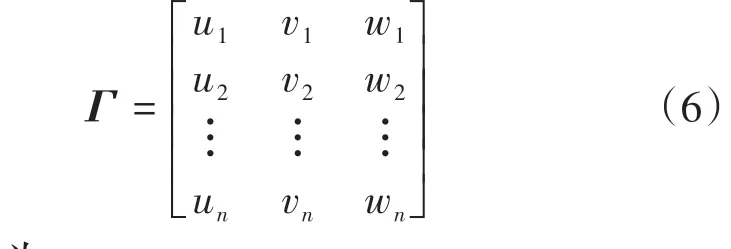
归一化系数为

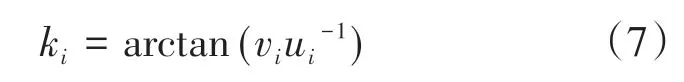
将ki并入Γ，获得归一化矩阵：

实测点云与理论点云配对，最小值偏离系数s的求解方法为

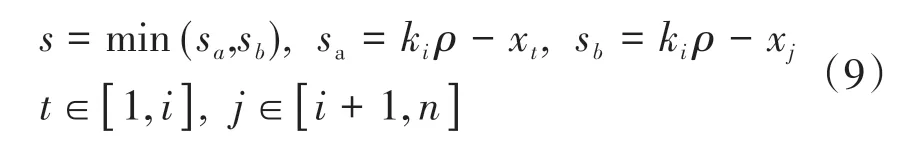
式中：t，j为正整数；d为被检轮廓度公差值；当s≤d/10，实际轮廓与理论轮廓完成坐标点的配对，根据式（9）可以确定搜索次数n。

3.2 全域评定方法

根据线轮廓度公差定义，被测点相对于理论点的位置定义成测量点相对于误差圆的相对位置。图4为测量点在包络组圆的分布情况，测量点在以理论点为圆心的4个象限内。图4a为点在圆内分布均匀，图4b在圆内向圆心聚拢，图4c为测量点聚拢于理论点圆心位置，图4d为被测点未被包络。

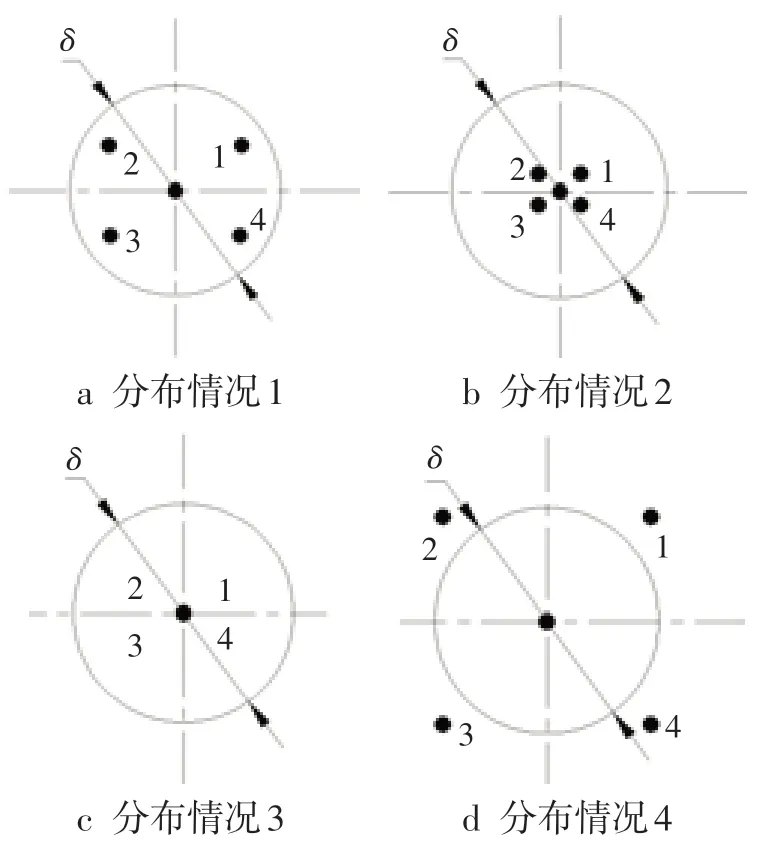
图4 测量点分布图

被检测零件型线轮廓属于空间三维曲线，为了准确评定该零件的线轮廓度，以已知理论轮廓点位置建立检测包络检测区域函数，通过包络组圆函数来评定全域内测量点相对于理论轮廓的位置关系，从而确定线轮廓度误差。线轮廓度全域评定原理如图5所示。

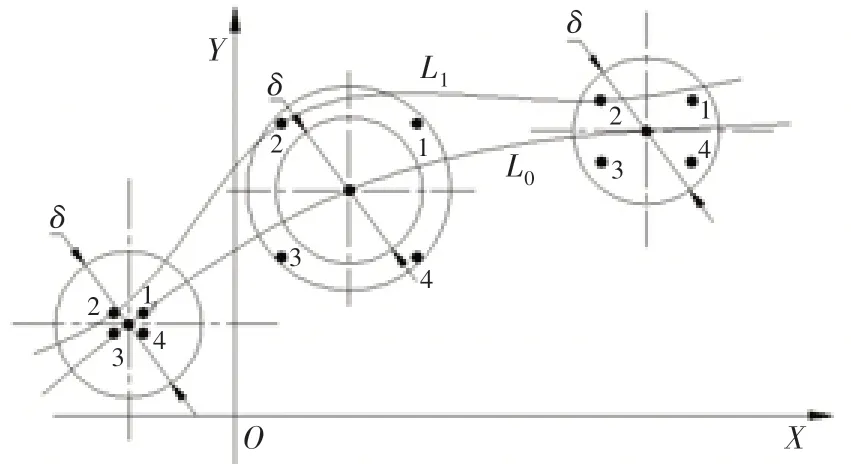
图5 被测轮廓度误差评定原理图

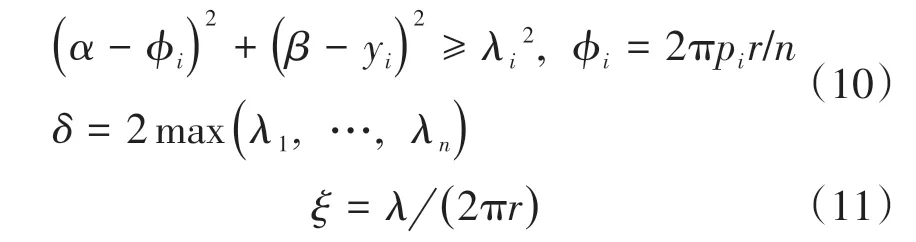
式中：α、β为分别误差圆x、y方向上的自变量；λi为包络圆的半径；φi为型线上第i个理论轮廓点展开后的X轴方向的分量；ξ为尺寸系数比。

全域内评估轮廓度值时，曲线形状与误差尺度量级不同，x偏小，不便于分辨和评估。对矩阵Γ、Π进行偏离处理，消除长度参数的尺度。在轮廓曲线维度处理后测量点用矩阵Μ表示：

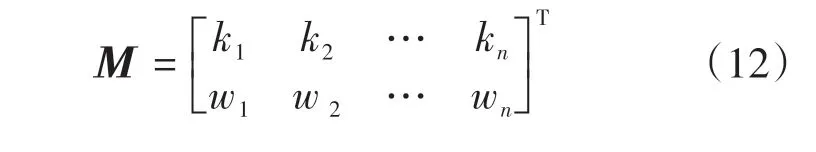
偏离值集合矩阵N2表示为

偏离值平方和用矩阵H表示为

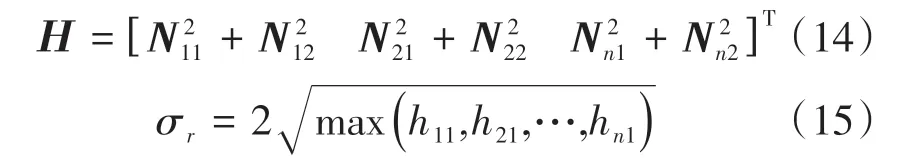
式中：σr为三维曲线的线轮廓度；Nn1为矩阵N中的元素；hn1为矩阵H中的元素。

4 实验结果分析

被测零件为某双离合变速器（DCT）换挡毂，选取直径为107.8 mm的圆柱作为截圆，获取理论轮廓和实测轮廓采样点，经纬度和离散化处理，得到其二维轮廓点云图。经式（9）归一化处理完成轮廓理论点与实测点的配对，如图6所示，型线展开后的配对情况如图7所示。

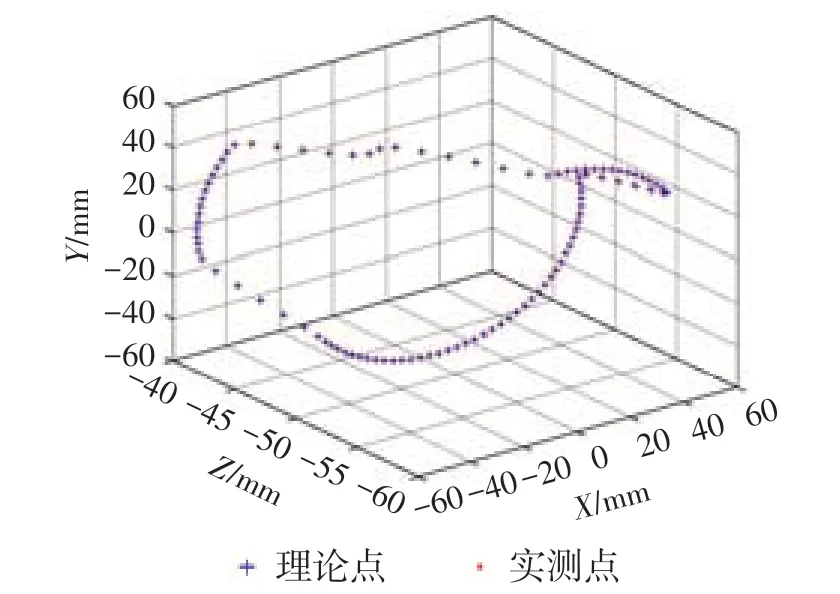
图6 轮廓采样点提取图

图7 轮廓理论点与实测点配对图

根据式（10）确定全域范围内包络组圆及评定方法，如图8所示。图9参照图4中点的分布情况，以点云中λ1最大值为半径和对应理论点为圆心，绘制被测轮廓全域评定误差图。在全域内随机选取局部位置点放大，可观察到测量离散点均包络于组圆内。获取理论点与实测点在敏感方向的差值，见图9，进一步显示被测零件轮廓的偏差实际情况。

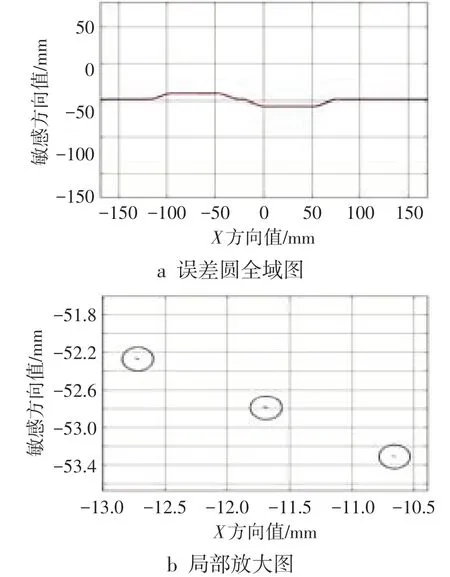
图8 轮廓线区域离散点评定误差图

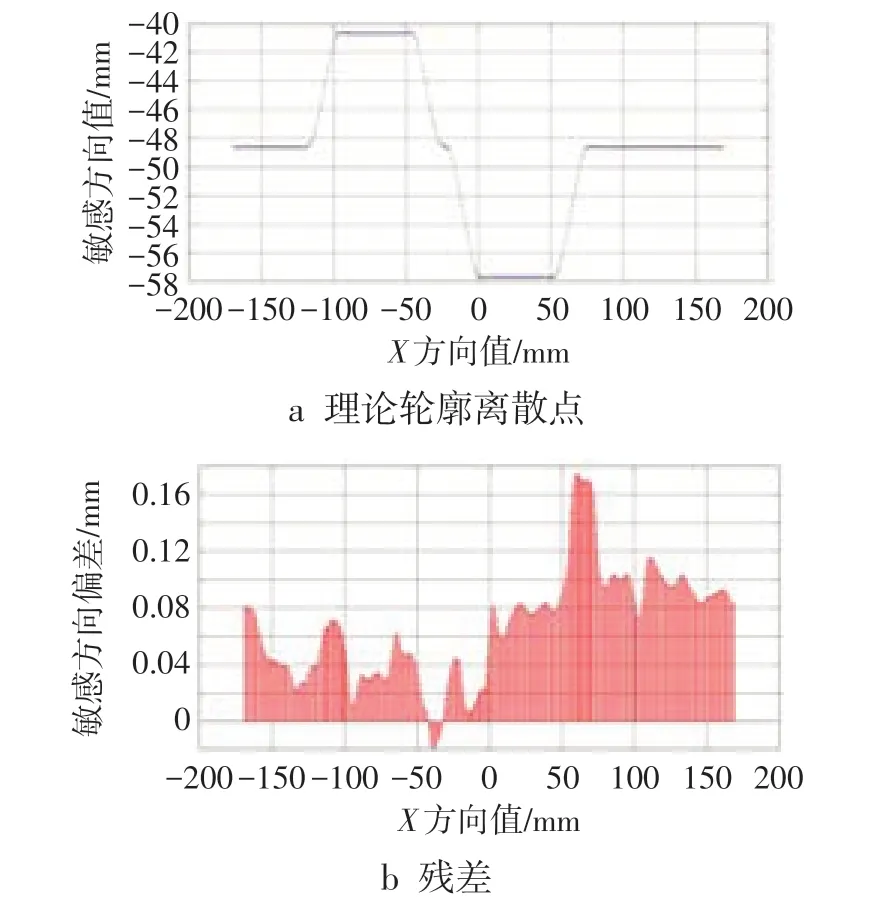
图9 轮廓全域残差图

为了更直观地显示全域内各个点的偏差，根据式（11）消去轮廓曲线长度元，对全域内检测点进行标记，方便检测结果可溯源到曲线的对应位置，如图10所示。利用式（14）搜寻到可包络全部采样点的圆，σr为0.350。溯源到全域内最大误差位置点为60，如图10b所示。

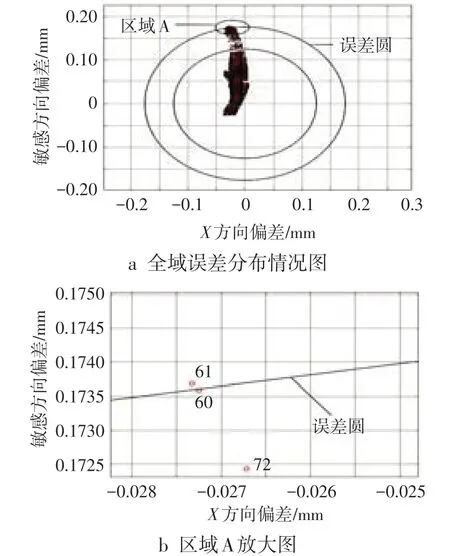
图10 轮廓度全域误差溯源图

包络圆内显示全域内点相对于理论点的位置和偏离的趋势，即轮廓度误差，通过点的标记号连续分布于包络圆，所对应的曲线相关区域测量点偏离理论轮廓幅度大。

5 结论

文中提出了三维曲线轮廓度全域评定方法，实验结果显示误差值为0.375 mm，符合误差范围要求，且检测结果可溯源到曲线的对应位置，同时构建组圆包络函数，实现轮廓度全域评定，该方法具有全局性，符合轮廓度定义。