高等数学解题反思与数学思维
郑丽娜,李应歧
(火箭军工程大学 基础部,陕西 西安 710025)
数学学习具有的抽象性、自我意识的作用突出,需要学习活动与对活动的自我反省调节的协调统一。然而,很多学生并没有意识到这一点,常常忽视基本的概念、定理的理解和掌握。高等数学[1]的学习过程中会遇到各种各样的题目,有些题目既需要基础知识又需要一定的技巧,而题目不是做得越多越好,关键是要进行解题反思,将知识内化,学会总结、提炼。本文以解题反思为切入点,对提升学生数学思维品质和解题能力进行研究。
1 数学解题反思的基本内涵
“反思”是指对自身的思维过程、结果进行再认知和检验的过程,是认知过程中强化自我意识、进行自我监控、自我调节的主要形式。反思是重要的思维活动,它是思维活动的核心和动力,是思维的关键点和切入点,可以促使思维更加精确化和概括化[2]。反思性学习是一种高效的学习方式,而解题反思是对解题活动的深层次思考。反思什么?对题意理解的反思,题目涉及知识点的反思,解题思路形成的反思,解题规律的反思,解题结果表述的反思,以及解题失误的反思等,例如,命题的意图是什么?考查的是什么概念、知识和能力,验证解题的结论是否合理?命题所提供条件的应用是否完备?解题过程是否判断有据,严密完善?是否还有新的解法等。
解题反思具有重要的意义,数学教育家波利亚说:“如果没有反思,他们就错过了解题的一次重要而有效益的方面。”通过回顾解题的整个过程,重新考虑和检查所求结果以及得出该结果的途径,可以深化对问题的理解、优化思维过程、揭示问题本质、探索一般规律、沟通新旧知识之间的联系,深化对知识的理解,从而发展解题的能力,提高学习的效率以及提升数学思维品质。
2 学生做题存在的问题
现今学生在大学数学的学习过程中很少有反思过程,更不用说解题反思。在做题时主要存在以下问题:
1)做题照葫芦画瓢。完全照搬老师上课讲的例题或者课本上例题的解答,做类似的题目,当题目有变形时,解答就出错,缺乏真正意义上的解题回顾。
2)做题只注重数量。一味追求多做题,不重视做题过程和反思,没有反思的意识和习惯。
3)做题只关心结果。做题只看结果,没有系统地掌握知识,纯粹靠死记硬背,没有真正领会解题的思想和方法。
4)做题不注重扩展。对于做过的题目不分析不拓展,面临新题或者灵活性比较强的题目时,往往没有思路,束手无策。
3 引导解题反思,提升数学思维品质
3.1 对题目的反思
3.1.1 引导多解,多角度反思
高等数学各知识点之间紧密联系,是一个完整的知识体系,解题的思路灵活多变,但最终殊途同归,引导学生关注一题多解,一题多变和多题一解。要引导学生反思问题本身,在做完某道题后要引导学生进行“头脑风暴”。根据题目的基本特征和关键因素,进行多方位、多角度的观察、联想与反思。反思该问题是否有新的解法,如果有则应分析比较,找出最佳解法,培养发散性的思维;还要反思能否对原题变式拓展,有些题目改变原题的结论或条件,可以把一道题变为多道题,从不同侧面理解题目涉及的知识点,提高思维的灵活性;更要对问题分门别类,通过对多样的或者不同问题的统一解法,有利于学生思维敏捷性的提高,在做题的过程中进行多元化思维,自主构建知识框架,全面把握各个知识点,从而培养学生的认知迁移、深刻理解、灵活应用以及解决问题的能力[3]。
案例1学习一元函数微积分时解决过下列问题:
1)如何求密度分布不均匀的细棒的质量?
2)如何求一根细棒对一个质点的引力?
3)如何求平面图形的面积?
学习多元函数微积分时解决过下列问题:
1)如何求密度分布不均匀的平面薄片的质量?
2)如何求空间一物体对于物体外一点处单位质量的质点的引力?
3)如何求空间曲面的面积?
4)如何求平面薄片的转动惯量?
多元函数积分学是一元函数积分学在空间中的推广,在学习多元函数积分学时,要联系一元函数积分学处理问题的思路与解题经验,将某些问题联系起来考虑,这样容易发现问题的实质与联系,找到一类问题的解决方法,而案例中的问题均需采用“微元法”分析求解。经过这样的反思,可以达到一题多解的效果,把书读薄,凝练提升,吸取精华,提高效率。
3.1.2 挖掘内涵,反思发现
一个好的数学问题往往有比较深刻的内涵,而发现一个问题远比解决一个问题更重要。如果在问题求解以后对题目进行反思,挖掘问题的内涵,将问题拓展延伸,找出新的问题,深化认识,这不仅有助于帮助学生举一反三,触类旁通,而且培养了思维的广阔性。

3.2 对解题过程的反思
3.2.1 尝试错误,反思纠正
有些题目采用正误对比,设置陷阱的方法,暴露出学生平时解题时容易犯的错误,让他们自己去探索错误的根源,反思问题的症结,这样对知识的理解更加深刻。
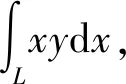

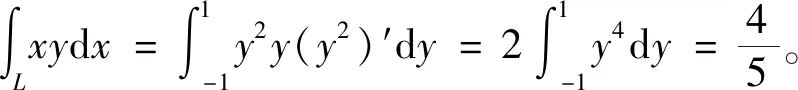

这是一道计算第二类曲线积分的常规题目,题目不难,但是很容易出错。在上述3种解法中,第1种解法利用对称性简化计算,第2种解法将曲线积分化为对y的定积分,第3种解法将曲线积分化为对x的定积分。看似都没有错误,但结果不一样,其中一定有错误的解法。这势必引起学生的好奇心,引导学生进行反思,产生认知冲突,经过分析讨论学生认识到3种解法均是错误的,从而让学生意识到计算第二类曲线积分时应注意的问题。这样对题目求解过程中的易错点进行反思,可以加深学生对该知识的印象,避免重蹈覆辙,破除思维定式。
3.2.2 转化思维,反思归纳


3.2.3 双向考虑,反思切入
从解题入手寻找解题途径的基本方法,从问题入手,寻找要想获得所求,必须要做什么,找到“需知”。将“需知”作为新问题,直到与“已知”所能获得的“可知”相沟通,将问题解决,也就是利用逆向思维分析问题,解决问题。此外,还可将函数变形,一般变形的方向是化繁为简,化抽象为具体,化未知为已知。题目中的已知条件和待求结论之间的桥梁建立是解决问题的关键。在分析已知条件和待求结论之间的差异的基础上,化归和消除这些差异,寻找差异是变形依赖的原则。

3.3 对“解”的反思
3.3.1 鼓励质疑,反思批判
案例6求曲线y=-x2+4x+3在其顶点处的曲率(答案为-2)。
这是学生在期末考试时的错误解答,虽然错误很明显(曲率不可能是负值),并且容易改正,但是学生因缺少反思的意识而未发现错误。当一个问题解决后,并不代表对该问题的思维活动已经结束,还要继续研究。教师在教学的过程中要引导学生反思题解,从是否符合实际、符合题意、逻辑过程、隐含条件等方面进行反思,鼓励持怀疑的态度,反思解的合理性与正确性,提升思维的批判性,提高做题的正确率。
3.3.2 思考全面,反思逻辑
案例7设有一圆板占有平面闭区域{(x,y)|x2+y2≤1}。该圆板加热,以致在点(x,y)的温度是T=x2+2y2-x,求该圆板的最热点与最冷点[1]。
这是一个最值问题,转化成极值问题解决。很多学生在做该题时,往往只是利用无条件极值的求法在区域{(x,y)|x2+y2<1}内求极值。反思错误的原因,主要是分类不全导致的,这实际上是无条件极值与条件极值的综合性问题,在区域内部属于无条件极值,在边界曲线上属于条件极值问题,必须分类讨论。
经验总结:高等数学中有一类问题考查学生的思维逻辑是否严密与正确,考虑问题是否全面,比如分类讨论就属于其中的一方面。通过引导学生这样反思,有助于加强学生思维的逻辑性,更加全面地考虑问题。
3.3.3 引导回顾,反思优化


当某些数学问题解决后,要反思得到的结论,进行思维过程的再验证与再认识,从“解”出发,将其作为条件,有时可以发现一些新的方法或者是更一般的求解方法,不仅可以将解题过程优化,推广解题的成果,还可以拓展学生思维的广度。
4 对解题反思提升数学思维与解题能力的进一步思考
4.1 学生数学思维障碍的表现
由于教师的教学脱离了学生的实际,且学生新旧知识不能顺利“交接”,导致学生形成数学思维障碍:思维形式或结果与具体问题的解决存在差异,主要表现在以下方面。
1)数学思维的肤浅性。只注重由因到果的习惯,不注重变换思维的方式,缺乏沿着多方面去探索解决问题的途径和方法;缺乏足够的抽象思维能力。
2)数学思维的差异性。在思维方法、速度以及思维的独立性和灵活性等方面存在差异。
3)数学思维的消极性。容易墨守成规,陷入思维定式。
4.2 破除思维障碍
教师要引导学生突破数学思维障碍,强调学生的主体意识与数学意识,引导他们认识其原有的思维框架,消除思维定式。而数学思维形成的困难主要由于教师“心中无生”,按照自己的思路或逻辑进行灌输式教学;学生在学习新知识时,没有架起新旧知识联系的桥梁,没完成知识建构。因此,要想突破数学思维形成的困难,教师要做到以下几点。
1)遵循学生认知发展的阶段性特点,照顾到学生认知水平的个性差异,强调学生的主体意识,发展学生的主动精神。
2)重视数学思想方法的教学,指导学生提高数学意识,如“因果转化”“类比转化”等。
3)消除思维定式。思维具有反映同一律(等值变形、等价变换),思维相似律(同中辨异、异中求同)等基本规律。思维的特性包括:概括性,概括性越高,知识的系统性越强,迁移越灵活;问题性,问题是数学的心脏,要注重问题的发现和解决过程;相似性,从已解决的问题中概括出思维模式,再去处理类似问题,进而形成新的模式,构成相似系列,即各种命题与方法的相似链。数学思维的模式主要包括以下几类。
逼近模式:正向逼近—顺推演绎法,逆向逼近—逆求分析法,双向逼近—分析综合法,反面逼近—反证法,模糊逼近—尝试探索法,近似逼近—极限法。
叠加模式:化整为零,以分求和。把问题归结为若干种并列情形的总和或者插入有关的环节构成一组小问题;处理各种特殊情形形成各种小问题,将它们适当组合、叠加而得到问题的一般解,如爬坡法、逻辑划分法、中途点法、辅助定理法;容斥原理。
变换模式:利用代数变换、三角变换、几何变换、相似变换等。
映射模式:几何法、解析法、向量法、极坐标法、参数法等。
4.3 策略
在运用解题反思提升学生的数学思维品质,提高高等数学的解题能力的探究中,教师要采取合适的策略:注重题目的设计,起到促进学生反思的作用;课堂上提供充足的反思时间与空间,合理留白,多让学生思考“怎么做”“为什么这样想”“还能怎么想”等,让学生有表述想法和疑惑的机会,做到知其然,亦知其所以然,还知其何由所以然[6];采取情境式教学,创设反思的情境,增强学生的解题体验;充分利用小组合作、围桌学习、项目学习、沉浸学习等学习方式;指导学生总结,鼓励他们采用思维导图的形式,构建知识网络,将各个知识联系起来;加强纠错,让学生相互之间进行错题展示与讲解,强化其对易犯错误的印象;讲授数学解题反思的内容以及方法等。

