应用多星的空间目标跟踪定位算法

乔鹏 吕晓宁 赵军锁 夏玉立 李济民 周瑶

(中国科学院软件研究所 天基综合信息系统重点实验室，北京 100190)

早期的卫星任务，卫星数量较少，星载探测设备种类较为单一，常常采用单星对空间碎片等空间目标进行定位与跟踪。单星定位算法仅具备被动测角信息时，只能通过激光测距的方式对空间目标进行定位，但激光测距机因测频的限制，受空间距离及空间环境的影响，探测空间碎片等空间目标的定位与跟踪误差较大[1]。随着探测领域的发展，与单星的空间目标探测能力相比，多星协同任务规划可以合理分配任务资源，结合各类卫星的在轨探测状态与约束，具有较强的适应性和较广的观测范围，可完成复杂的观测任务[2]。因此，基于卫星搭建多星光学探测体系，解算空间碎片等空间目标的空间位置，实现空间目标的定位与跟踪具有重要的研究意义。

近年来，基于卫星解算空间碎片等空间目标方面，国内外已开展多项研究。文献[3]中研究了天基观测空间碎片等空间目标的光谱特性，从而获得空间目标的材料成分信息，为后续研究提供信息基础。文献[4]中分析了空间碎片探测谱段的响应程度，采用多光谱光学载荷进行空间碎片的探测，为空间碎片定位提供数据基础。文献[5]中对天基观测空间碎片等空间目标进行建模，分析系统误差对探测精度的影响，并设计有效方法抑制观测与模型结构误差对探测精度的影响。文献[6]中首先分析了空间碎片成像特性，构建二维高斯拟合模型，采用核函数的设计，监测空间碎片。但是，采用单星激光测距的方式，成像轨迹受到距离与空间环境的影响，进而影响定位精度。现有空间碎片探测技术在空间坐标系中目标定位与航迹管理方面，其目标定位精度问题依旧面临巨大挑战，同时光学探测体系还会出现空间目标的星间信息丢失、卫星与目标共面场景。因此，本文面向多星探测领域，提出一种多星空间目标跟踪定位算法。该算法基于三角交会原理[7]，建立空间坐标转换模型与多星定位模型，关联空间目标像点，解算空间目标轨迹，跟踪空间目标。当产生空间目标信息丢失等异常情况时，引入加速度参数建模目标轨迹，改进卡尔曼滤波算法预测空间目标轨迹位置。

1 空间目标跟踪定位算法

1.1 天基探测系统空间目标观测模型

首先，构建分布式天基探测系统总体架构，搭建天地基一体化、柔性可变的协同系统，将多星分为中央控制卫星、中间信息传输卫星和底层执行卫星，如图1所示。天基探测系统包括3个层级的卫星和地面控制中心。①第1个层级为中央控制卫星，该类卫星具有较强的智能性，是协同观测系统中的主导者，可完成协同任务规划、智能决策等工作。②第2个层级为中间信息传输卫星，该类卫星只做数据中间通信，负责底层执行卫星与中央控制卫星的通信。③第3个层级为底层执行卫星，该类卫星可实现终端智能，包括空间目标发现、识别、跟踪，以及小范围任务规划功能。④地面控制中心包括系统控制中心与指令跟踪站，它与中央控制卫星承担着系统的最高智能决策和任务分配功能，是系统的核心组成部分。

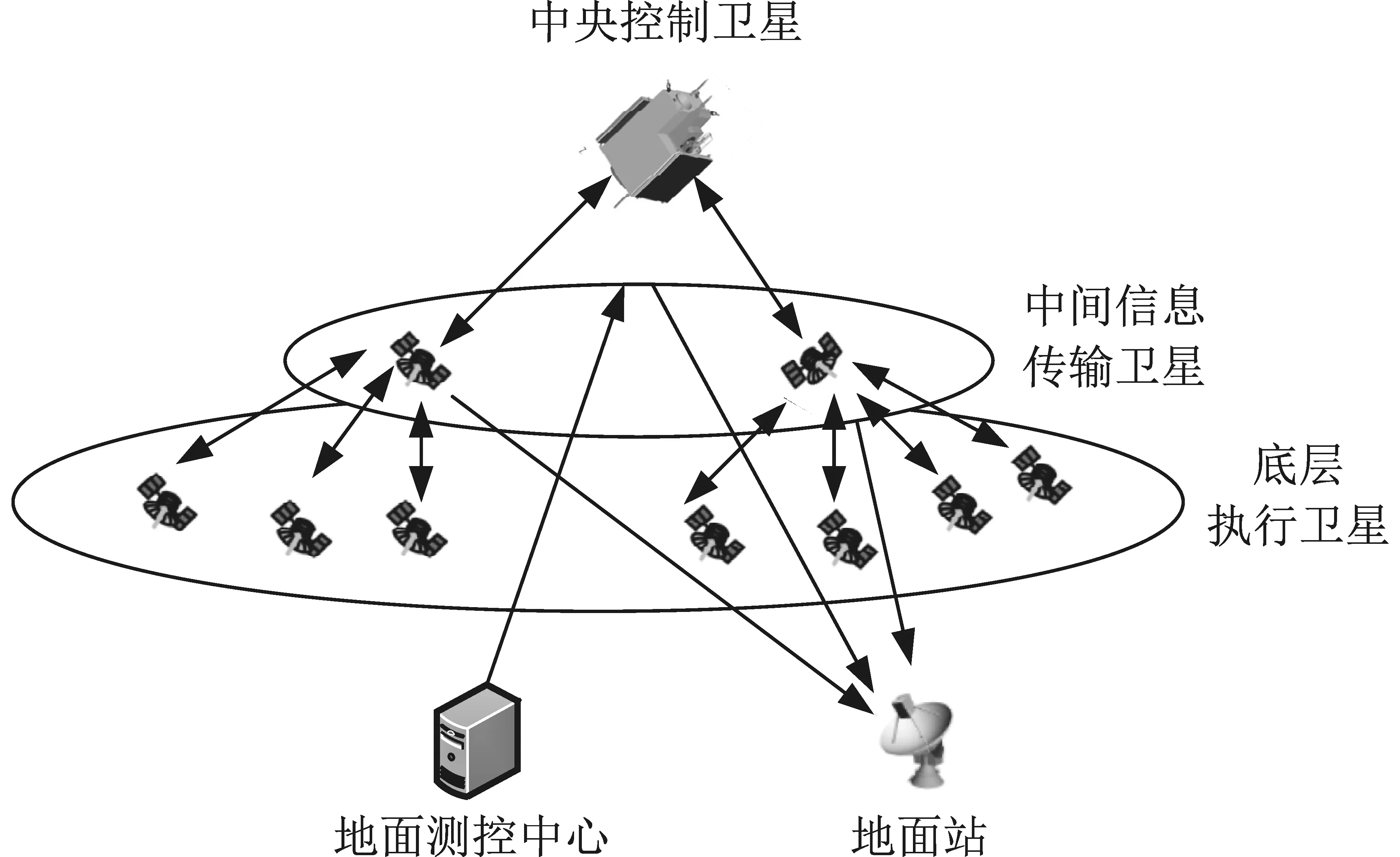
图1 天基探测系统架构Fig.1 Architecture of a space-based exploration system

天基探测系统可合理分配卫星资源，排列不同的时间窗，制定多星观测空间目标的任务规划，构建多星观测空间目标的交会模型，通过中央控制卫星控制底层执行卫星进行空间目标的观测定位。通过对多星坐标及空间目标坐标的三角交会原理，可以实现空间目标的位置解算。同时，各卫星数据统一到同一坐标系下进行交会解算。天基探测系统对多空间目标跟踪时，可获得空间目标相对于当前卫星坐标下的方向数据，方向数据与卫星高精度位置姿态数据结合转换到交会坐标系下。

天基探测系统采用异址双星方式，中央控制卫星确定系统观测任务在统一时序控制下，各星对空间目标进行同步观测，通过多星交会解算空间目标轨迹。以双星异面交会算法在相机自身坐标系下为例，如图2所示。图2中，设坐标系为O-XYZ,光学卫星1位置O1坐标为[X01Y01Z01],空间目标(位置T)相对于光学卫星1的方位角与俯仰角为A1,E1，并且构成一条空间射线O1T1；光学卫星2位置O2坐标为[X02Y02Z02],空间目标(位置T)相对于光学卫星2的方位角和俯仰角分别为A2,E2，并且构成另一条空间射线O2T2。因实际光学设备的观测误差，双星与空间目标间的向量称作异面直线[8]。天基探测系统下的底层执行卫星进行观测空间目标任务，空间目标成像投影与坐标系转换统一为J2000坐标系。空间目标(位置T)相对于光学卫星1和2的方位、俯仰角需要进行坐标转换，转换步骤如下。

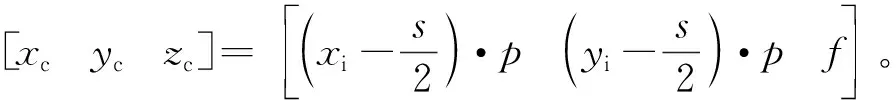
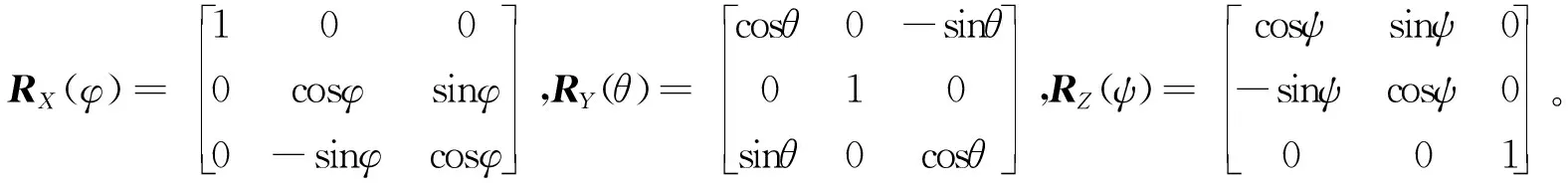
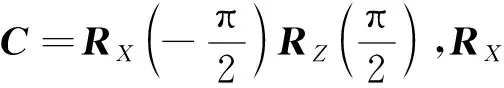
(4)地心轨道坐标系转至J2000坐标系。将轨道面旋转至与赤道面重合，需要进行3次坐标旋转，通过轨道六根数可以得到轨道倾角γ、升交点赤经Ω和升交点角距u，则空间目标(位置T)在J2000坐标系下的坐标可表示为[xECIyECIzECI]T=H-1[xpypzp]T。其中：H=RZ(u)RX(γ)RY(Ω)。

利用J2000坐标系下的空间目标(位置T)相对于光学卫星1和2的坐标[xECI1yECI1zECI1]和[xECI2yECI2zECI2]，可由式(1)解算出空间目标(位置T)相对于光学卫星1和2的方位角A1、俯仰角E1与方位角A2、俯仰角E2。

(1)

设图2中异面直线O1T1和O2T2的公垂线为l12,T1和T2分别为2条异面直线与其公垂线的交点，坐标分别为[X1Y1Z1]和[X2Y2Z2]。理论上，空间目标在异面直线O1T1和O2T2的公垂线上，确定卫星间空间目标像点关联关系，可交会确定空间目标的坐标。

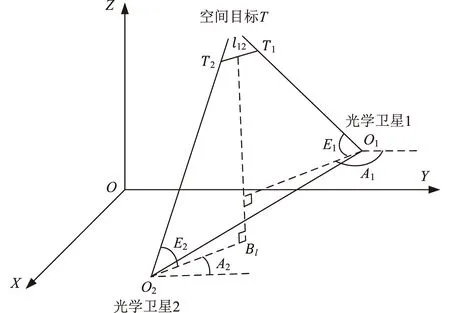
图2 双星交会算法原理Fig.2 Schematic diagram of double-satellite intersection algorithm

1.2 卫星间空间目标像点关联

坐标系转换后，天基探测系统的底层执行卫星之间需要计算不同像点之间的异面直线距离，关联同一空间目标的星间像点。利用第1.1节像面坐标转至J2000坐标下的步骤，假设像点i相对于光学卫星1的空间坐标为[X1iY1iZ1i],像点j相对于光学卫星2的空间坐标为[X2jY2jZ2j],光学卫星1的坐标为[x1y1z1]，光学卫星2的坐标为[x2y2z2]。具体求解的数学表达式为

(2)

式中：[dij]为2颗卫星间不同像点之间的异面直线距离矩阵。

计算出像点间的异面直线距离矩阵，当作最优化问题的匹配成本矩阵，这样可通过最优化算法，最小化总匹配成本，找到同一空间目标在不同卫星所成像点的对应关系，以及同一空间目标在不同时刻所成像的对应关系。本文采用最近邻点算法[9]将星间像点最优匹配问题建模为赋权二分图求最优解的问题，原理为：若任意一个相等的子图距离最近，可作为子图的完美匹配，即匹配成本最小的一组匹配结果，得出已经完成匹配的空间目标标志号，以及匹配失败的星间的空间目标标志号。

1.3 空间目标的跟踪与定位

最优化求解出星间像点匹配关系，基于双星交会模型解算空间目标轨迹及误差计算公式[10]，分析影响定位精度的因素。

(3)

式中：m1，m2，K，l1，l2分别为光学卫星1和2交会模型的中间变量。

(4)

式中：加权系数ρ∈[0,1]；[xyz]为空间目标坐标。

这样，求解出空间目标的坐标，便可对其进行跟踪定位。

1.4 异常情况下的空间目标跟踪

天基探测系统在轨观测运行时，若空间目标观测过程中出现星间信息丢失、空间目标与卫星共面情况，多星定位算法对空间目标的坐标预测误差较大，跟踪精度较低。

天基探测系统观测空间目标出现异常情况时，通过中间信息传输卫星将异常行为指令反馈给中央控制卫星，中央控制卫星发出算法处理指令，底层执行卫星执行加入加速度分量的卡尔曼滤波算法[11]，预测空间目标在当前帧的轨迹位置，进而完成空间目标跟踪任务。

传统卡尔曼滤波算法[11]的目标轨迹建模如下。

(5)

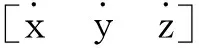
(6)

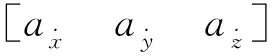
卡尔曼滤波算法首先采用时间更新方程来预估空间目标的坐标位置，时间更新方程为

X(k|k-1)=AX(k-1|k-1)+BU(k)

(7)

P(k|k-1)=AP(k-1|k-1)AT+Q

(8)

式中：X(k|k-1)为k时刻的过程状态；X(k-1|k-1)为k-1时刻的最优状态；A为状态转移矩阵；B为系统参数；U(k)为系统的调控量；P(k|k-1)与P(k-1|k-1)为k与k-1时刻状态对应的协方差；Q为高斯白噪声。

时间更新方程以当前状态作为初始状态，基于空间目标轨迹向量预测下一帧的空间目标状态，即空间目标的坐标；预测完空间目标的位置，卡尔曼滤波算法采用状态更新方程进行校正，状态更新方程为

Kg(k)=P(k|k-1)HT/(HP(k|k-1)HT+R)

(9)

式中：Kg(k)为卡尔曼增益；H为观测矩阵；R为测量噪声对应的协方差矩阵。

X(k|k)=X(k|k-1)+Kg(k)(Z(k)-

HX(k|k-1))

(10)

式中：Z(k)为k时刻的观测值；X(k|k)为k时刻的最优状态。

P(k|k)=(I-Kg(k)H)P(k|k-1)

(11)

式中：I为单位矩阵；P(k|k)为X(k|k)状态对应的协方差。

采用状态更新方程将时间更新方程预测的轨迹位置与监测位置作差值，计算误差协方差矩阵，迭代优化，得到空间目标的坐标值，进而跟踪空间目标。

2 实例验证

2.1 测试用例

通过STK软件构建理论空间目标数据和观测卫星的数据，模拟天基探测系统的卫星组网情况，构建4颗卫星组网观测16个目标从太原飞往非洲的场景，具体的场景示意如图3所示。其中：M1～M16为空间目标，飞行高度为550 km,飞行时长约为660 s。卫星对空间目标的可见时间段(日期2021-05-05,20帧每秒数据)分布如表1所示，其中持续时间为总帧数除以每秒帧数计算得出。

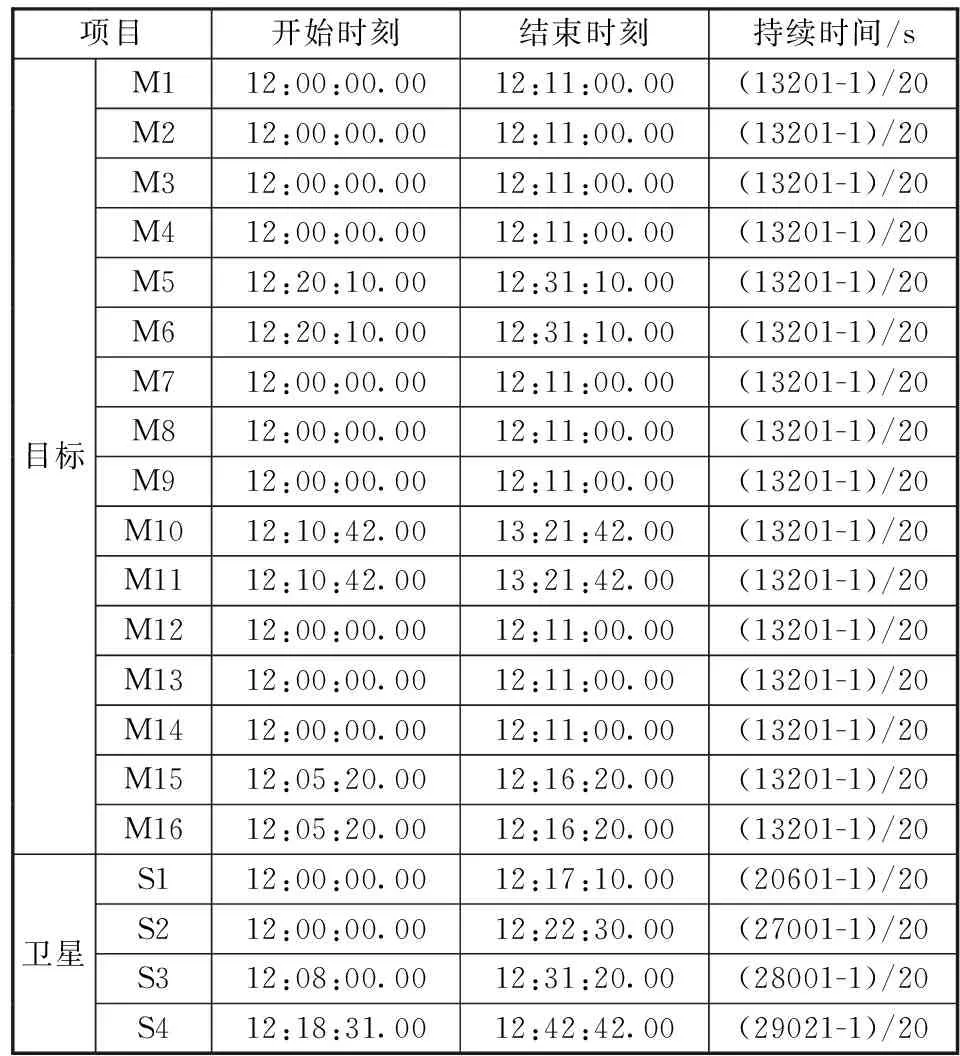
表1 卫星对空间目标的可见时间段Table 1 Observable time periods of satellites to space targets

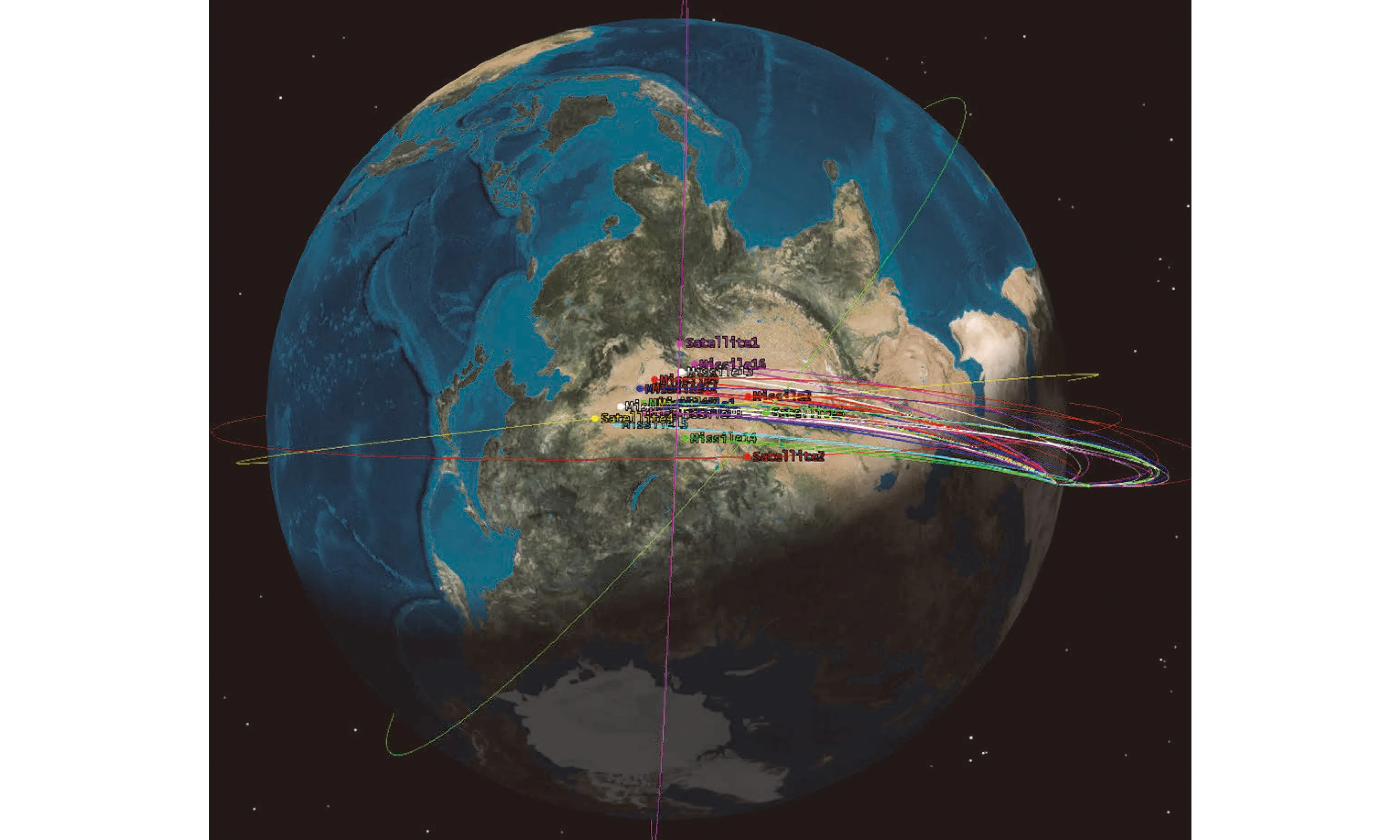
图3 天基探测系统的卫星组网仿真Fig.3 Satellite networking simulation of space-based exploration system

取卫星编号S2与S3执行双星观测空间目标定位任务，测试用例见表2，共870 s的观测数据，进行空间目标的跟踪与定位。

表2 测试用例Table 2 Test case

实际卫星探测空间目标存在测量误差，为模拟真实场景，本文附加的卫星站点位置误差为15 m,卫星对空间目标的俯仰角与方位角误差均为15″。

2.2 空间目标定位误差分析

利用第2.1节的测试用例测试本文算法的可行性，测试空间目标定位算法的精度与跟踪情况，如图4所示。

由图4可看出：X，Y，Z方向的位置误差均在10 m以内，X方向的速度误差在6 m/s以内，Y方向的速度误差在8 m/s以内,Z方向的速度误差在4 m/s以内。在前面15 s，X，Y，Z方向位置与速度误差稍高一些，分析卫星间的空间目标关联匹配需要一定的匹配时间，最近邻算法匹配性能才能达到最优。持续一段时间后，算法趋于稳定状况，位置误差与速度误差较低。

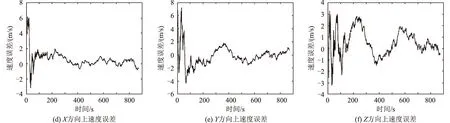
图4 位置与速度误差分析Fig.4 Position and velocity error analyses

下面统计本文算法对空间目标轨迹解算跟踪的情况。成功跟踪时，标志位置1；若未跟踪，标志位置0。在870 s的观测数据内，实时统计其空间目标跟踪的准确率，具体如图5所示。可以看出：采用本文算法，前15 s进行星间空间目标点的匹配关联，15 s之后进行空间目标跟踪处理，当天基探测系统底层执行卫星对空间目标的观测数据一直存在时，采用本文的算法便能解算出空间目标轨迹，成功跟踪空间目标。

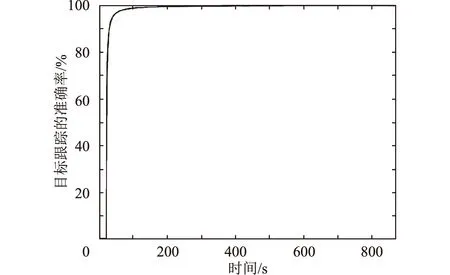
图5 本文算法的空间目标轨迹解算情况Fig.5 Space target trajectory solution of algorithm in this paper

2.3 异常情况下空间目标跟踪分析

当空间目标存在星间信息丢失、空间目标与卫星共面时，基于仿真输入的测试用例，将编号S3卫星在12:12:00.00-12:12:20.00和12:16:00.00-12:16:20.00时间段内对空间目标的观测数据作丢失处理，采用本文算法的跟踪状态见图6。

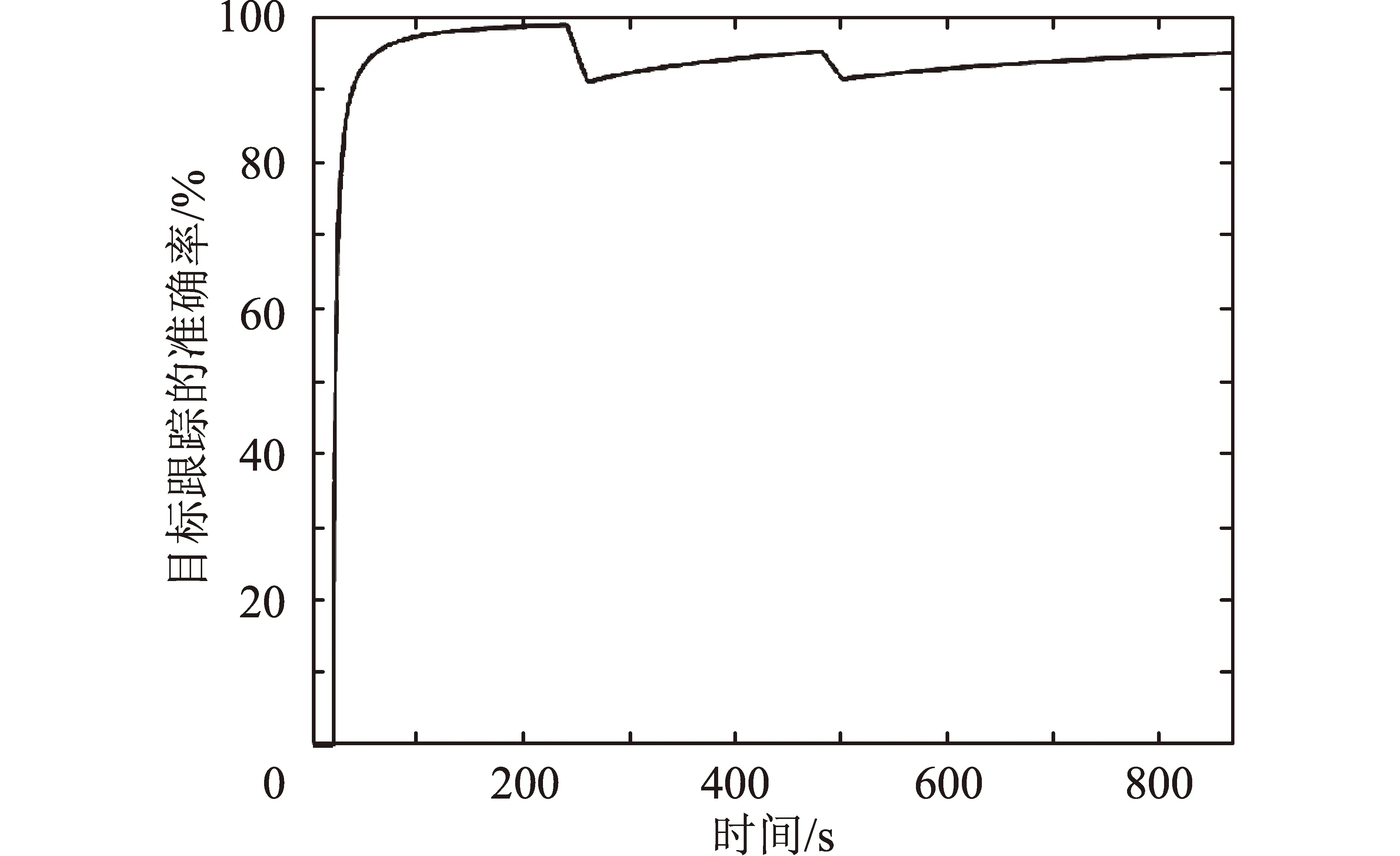
图6 异常情况下空间目标跟踪状况Fig.6 Space target tracking status under abnormal conditions

底层执行卫星采用加入加速度分量的卡尔曼滤波算法预测空间目标在当前帧的轨迹位置，采用本文算法的跟踪状态见图7。可以看出：辅以前面几帧空间目标的位置、速度、加速度建模目标轨迹向量，结合卡尔曼滤波算法能有效提高空间目标的跟踪精度。

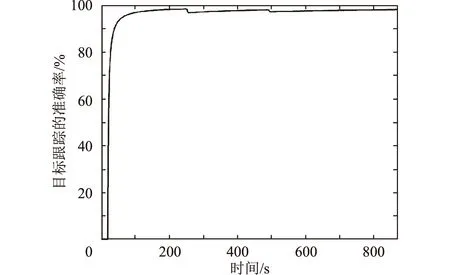
图7 异常情况下卡尔曼滤波算法空间目标跟踪状况Fig.7 Space target tracking status of Kalman filter algorithm under abnormal conditions

3 结束语

本文构建分布式天基探测系统总体架构，提出一种多目标跟踪定位算法。该算法面向多星不同载荷平台进行坐标转换，计算观测空间目标的异面直线距离，采用最近邻算法最优匹配同一空间目标在不同卫星所成像点的对应关系，进而解算空间目标轨迹与空间目标跟踪；当产生空间目标与卫星共面等异常情况时，本文构建目标轨迹向量引入加速度参数，采用卡尔曼滤波算法预测空间目标轨迹位置。通过STK软件仿真数据进行实例验证，结果表明：该算法的定位精度更高，当出现卫星间的空间目标信息丢失的场景时，结合卡尔曼滤波算法能有效提高空间目标的跟踪精度。

本文算法可应用于天基观测系统，完成在轨实时处理，工程可实施性强，可为分布式天基探测系统在轨监测空间碎片提供一种高效途径；但该算法在双星交会角处于180°周围时存在测量条件劣化，导致探测空间目标轨迹时产生测量误差，进而影响定位结果，下一步将重点研究该异常情况，构建合理的误差传递模型，提高算法对异常情况的普适性。