基于改进NSGA-II的车间排产优化算法研究
周原令,胡晓兵,江代渝,李 航
四川大学 机械工程学院,成都 610065
随着制造行业排产技术的飞速发展,智能排产调度技术[1]已经成为智能制造的关键技术,运用手工进行排产已经渐渐地阻碍了制造业智能化发展的进程。智能排产[2-3]是指在工艺及资源等的约束条件下,根据设备生产能力,建立任务分配模型,并利用智能算法对任务进行合理的分配,确定任务的开始加工时间。智能排产是生产管理的核心,也是企业调度的大脑。智能调度[4]是以智能排产为核心,根据排产结果在实际生产过程中受到扰动因素(机器故障、订单临时取消及插入等)后,通过对排产算法基础参数进行修正(或者重新设计重排产算法),然后重新进行排产的一个动态过程,是智能排产技术的验证及延伸。通过智能排产技术实现生产线的快速排产[5]和实时调度,能够大大降低企业的生产成本,时间成本和订单预估成本。
排产问题是典型的NP-Hard问题[6]。排产对于降低企业生产成本、保证交期等都是至关重要的。排产优化算法研究的问题一般是典型的多目标优化问题[7-8]。1954 年,Johnson[9]就提出了车间排产的相关概念,其对两台机器下作业排序问题的求解已经成为了经典排产理论产生的重要标志。随着排产问题不断受到企业的重视,越来越多的学者对其进行了研究。20世纪中期,丰田公司提出并将JIT(Just-in-Time)算法[10]应用到企业的生产排产与调度过程。Kubiak 等[11]利用动态规划方法求解得混流装配线排程问题最优解。Benkalail 等[12]针对并行工位的置换流水车间的排产优化问题,提出一种采用改进后的候鸟优化算法解决车间排产优化问题。Manupati 等[13]针对存在准备时间影响下的多目标排产优化问题,提出了一种新的基于多目标的进化人工免疫非主导排序遗传算法(AI-NSGA-II),并证明了其算法的有效性。近年来,国内的学者们对智能排产算法的研究越来越多,Xia 等[14]用微粒群优化算法求解机器分配问题,用模拟退火算法求解操作排序问题,通过二者集成的思想求解多目标柔性作业车间排产问题。钱忱等[15]运用线性规划模型搭配降维算法进行排产问题优化求解,提高了系统运算速度。随着研究的深入,开始将排产算法大量的尝试在NSGA-II(Non-dominated Sorting Genetic Algorithm-II)经典算法上,并不断的改进。冯翔等[16]提出了基于最近邻思想的启发式交叉算子和改进的变异算子,并对非劣解进行筛选的改进NSGA-II(Improved Non-dominated Sorting Genetic Algorithm-II)排产调度算法,研究多跑道飞机进港航班排产调度问题。林进等[17]提出基于嵌套正交搜索策略的改进NSGA-II 算法,引入模糊时间窗,解决班轮延误后船期恢复的重排产调度问题。刘东等[18]提出了一种基于雄狮选择法的改进NSGA-II算法,针对NSGA-II算法选择缺陷,保护优秀个体的水库双目标优化排产调度问题。本文重新研究NSGA-II算法的优缺点,结合生产实际,提出基于改进均匀进化精英策略和改进自适应交叉和变异算子的改进NSGA-II算法,将迭代次数和算法优化联系起来,提高种群多样性的同时,提高运行速度,加速收敛,避免陷入局部最优解,最后运用排产优化实例,证明改进NSGA-II算法的优越性。
1 问题描述及建模
1.1 问题描述
含能行业离散车间的排产问题一般可描述为:有a种类型的n个产品,按照某种约束顺序,在b种类型的m台机器上进行加工,每个产品有k道加工工序。相同类型产品的同名工序在同种机器上加工;每种类型的机器只能加工一道工序;同一产品的加工必须遵循工序约束,即上道工序结束才能进入下一道工序的加工;不同产品不能同时使用同一台机器。
1.2 约束分析
将实际排产调度过程中的客观条件影响及约束进行分析,建立生产理想模型,实现排产调度的行业通用性。运用5M1E(人机物法环测)分析法[19],建立车间约束条件,并做出相关假设:
(1)不同类型产品不能全部在同一条生产线上进行加工。
(2)相同类型产品在加工过程中不能同时同步加工。
(3)在安排产品加工过程中不考虑设备故障问题,产品只要被安排在某一要求时间段加工,就能按时正常完成加工。
(4)产品的最早开工日期不得早于订单签订日期。
(5)排产日期至少要比计划日期早一个生产周期。
(6)不同类型产品在某一工序借用其他产线设备时,不能影响相关设备产线的正常生产计划。
(7)同类型不同产品加工转换时,需要留有一定时间的间隔期,保证对机器进行清洗,其间隔时间由历史经验获得。
1.3 车间具体排产问题描述
产品n在t时刻在m台机器设备集上加工q千克,其中产品n包括k道工序。同种类型产品有相同的产品加工顺序,每道加工工序需在相应工序的加工机器上进行加工,并且已知加工时间,同类型产品仅在产品配方和产品加工时间上有差别,在加工顺序和加工工序上没有加工机器不通用的条件。
1.4 车间排产优化目标选择
考虑到含能离散行业的生产均衡性、紧凑性,本文选用对排产合理性和交货保障性最具可靠度的两个目标建立优化目标函数,并以目标函数均值为目标优化标准。
S1:最大化最小交货提前期,其计算如公式(1)所示:

其中,Rnl表示第l条订单记录中,产品n的交货日期,TFnl表示第l条订单记录中,产品n的计划完工日期,在算法优化过程中对其进行最小化处理。
S2:最小化最大理想加工时间偏差,其计算如公式(2)所示:

其中,TFnl表示第l条订单记录中,产品n的计划完工日期,TSnl表示第l条订单记录中,产品n的计划开工时间,TBnl表示第l条订单记录中,产品n的理想加工时间。
2 改进NSGA-II算法设计
2.1 传统NSGA-II算法介绍
1994年,Srinivas和Deb[20]为解决传统方法目标函数受权重影响较大的缺点,提出了NSGA(Non-dominated Sorting Genetic Algorithm)算法。随着研究的深入,Deb 等[21]又针对NSGA 算法时间复杂度高,共享参数不能定量等缺点进行改进,并根据基于精英策略的遗传算法研究,提出了基于精英保留策略的快速非支配排序算法即NSGA-II算法。
NSGA-II算法的一般操作步骤包括初始化种群,对种群进行快速可支配排序并正常产生子代种群,合并父代和子代种群为新种群,对新种群进行快速非支配排序,计算各支配前沿个体拥挤度距离,运用精英保留策略选择拥挤度较高个体组成新的父代种群,判断是否满足最大迭代次数,满足则终止算法,输出最优Pareto 非劣解集,不满足则对种群进行快速非支配排序产生子代种群,按照上面步骤进行循环。传统NSGA-II算法的流程图如图1所示。

图1 NSGA-II算法流程图Fig.1 Flow chart of NSGA-II algorithm
2.2 改进分类自适应交叉和变异概率
交叉和变异操作是种群个体更新的重要途径。为了合理的把握种群的更新及变异范围,本文提出基于分类自适应种群个体交叉和变异概率[22-23],将种群个体的更新范围随进化代数的增加而动态进行调整,增加种群的收敛性和搜索方向准确性。交叉概率通常选择在0.4~0.8之间,变异概率通常选择在0.1~0.001之间。

其中,pcagv表示平均交叉概率;pcmax表示最大交叉概率;pcmin表示最小交叉概率;d(i)表示当前种群选择变异的种群个体拥挤度;dagv(i)表示当前种群个体的平均拥挤度;pmagv表示平均交叉概率;pmmax表示最大交叉概率;pmmin表示最小交叉概率;genmax表示种群最大迭代值。公式根据个体拥挤度与种群平均拥挤度之间的关系,确定交叉和变异概率的进化方向,实现分类进化;同时引入迭代因子,实现种群的自适应进化,加快收敛速度。当个体拥挤度距离小于平均拥挤度距离时,随着迭代次数的增加,种群的交叉和变异概率越趋向中位值;当个体拥挤度距离大于平均拥挤度距离时,随着迭代次数的增加,种群的交叉和变异概率越小。
2.3 改进均匀进化精英保留策略
精英保留策略[24-25]是加快种群收敛的主要方法之一。基于种群多样性的考虑,对种群个体按照可支配层均匀抽取满足进化要求的种群群体;同时结合迭代进化规律,第一优先Pareto前沿采用基于种群迭代次数的累增加权策略,同时把加权于第一层的权重均匀递减给其余各层,保证种群整体稳定性及多样性的同时,使种群快速的向最有解的方向收敛。如公式(11)和(12)所示:
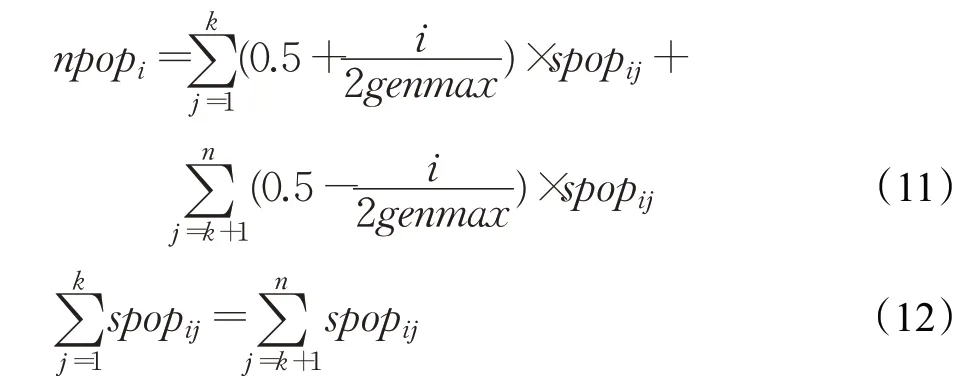
其中,npopi表示第i代的种群保留个体,spopij表示第i代第j可支配层的个体数量,genmax表示种群的最大迭代值。改进均匀进化精英策略原理图如图2所示。
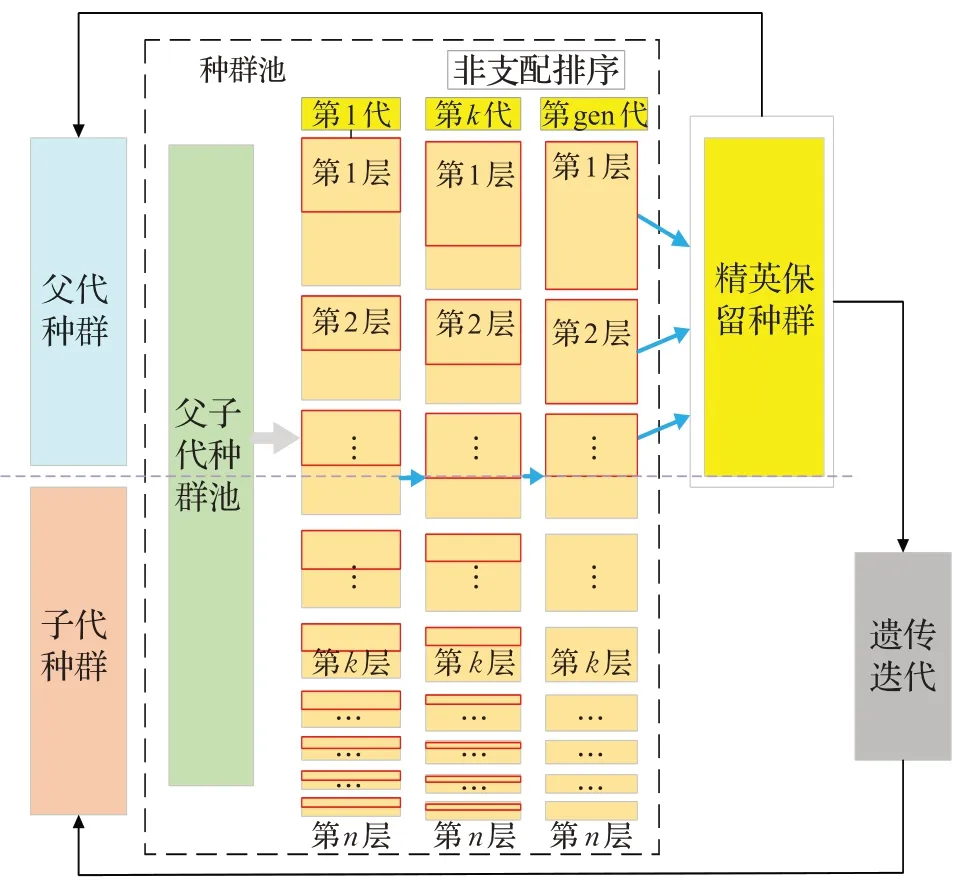
图2 改进均匀进化精英策略原理图Fig.2 Schematic diagram of improved uniform evolution elite strategy
2.4 改进NSGA-II算法设计过程
2.4.1 种群编码
对生产信息进行预处理,根据排产特点,将染色体编码为基于产品和日期的二维基因矩阵染色体。其编码染色体模型如下所示:
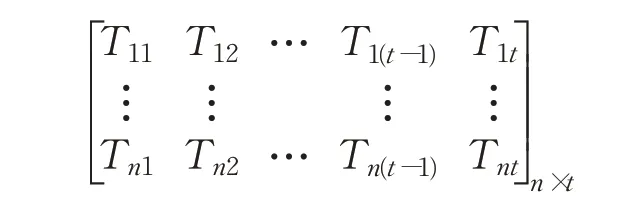
其中,n表示产品,t表示计划日期,Tnt表示产品n在t时刻是否投料。
2.4.2 种群初始化
本文根据实际生产排产特点,采用随机数法、定则生成法和基因块法按照黄金分割比规则对种群进行初始化,产生较优初始化种群[26]。种群初始化具体的生成方法,参考文献[26]中有详细介绍。
2.4.3 选择操作
通过拥挤度和非支配排序,运用轮盘赌法进行动态比例选择进入下一代种群的数量,保证种群多样性同时,增加种群个体锐度。
2.4.4 交叉操作
根据实际问题的特点,选择基于位置和产品优先生产权级并行混流交叉策略。其中,产品优先级通过专家评分法[27]对评价参数(产品成本利润空间系数、订单客户重要度系数、订单交货紧急程度系数、订单质量要求系数)进行综合打分求均值确定。采用本文设计的改进的自适应交叉概率进行交叉种群个体的选择。
2.4.5 变异操作
通过对生产实形目的导向性进化,选择基于位置的相邻区域镜像重组变异策略。采用本文设计的改进的自适应变异概率进行变异种群个体的选择。
2.5 改进NSGA-II算法步骤及流程图
步骤1设置算法基础参数包括种群规模pop,迭代次数genmax,预处理参数(订单oij),交叉和变异概率极值(pcmax、pcmin、pmmax、pmmin)。
步骤2初始化种群npop0,初始化种群迭代次数t=1。
步骤3根据改进交叉和变异率策略产生子代种群npopt。
步骤4合并父代种群和子代种群得到一个种群规模为2pop的新的种群池种群spopt,spopt=npopt+npopt-1。
步骤5计算新种群spopt中个体的目标函数值。
步骤6根据Pareto前沿,构造种群非支配层个体集合Ft={Ft1,Ft2,…,Ftk,…,Ftn} 。
步骤7计算种群各层非支配个体拥挤度距离d(i),并计算种群的平均拥挤度距离dagv(i)。
步骤8根据拥挤度排挤机制结合改进精英保留策略从spopt中,选择pop个个体,组合成为一个新一代的父代种群
步骤9对种群进行选择、改进变异概率策略的交叉和变异操作,产生新一代的子代种群npopt。
步骤10合并新的父代种群和子代种群npopt,得到新的种群池种群spopt+1。
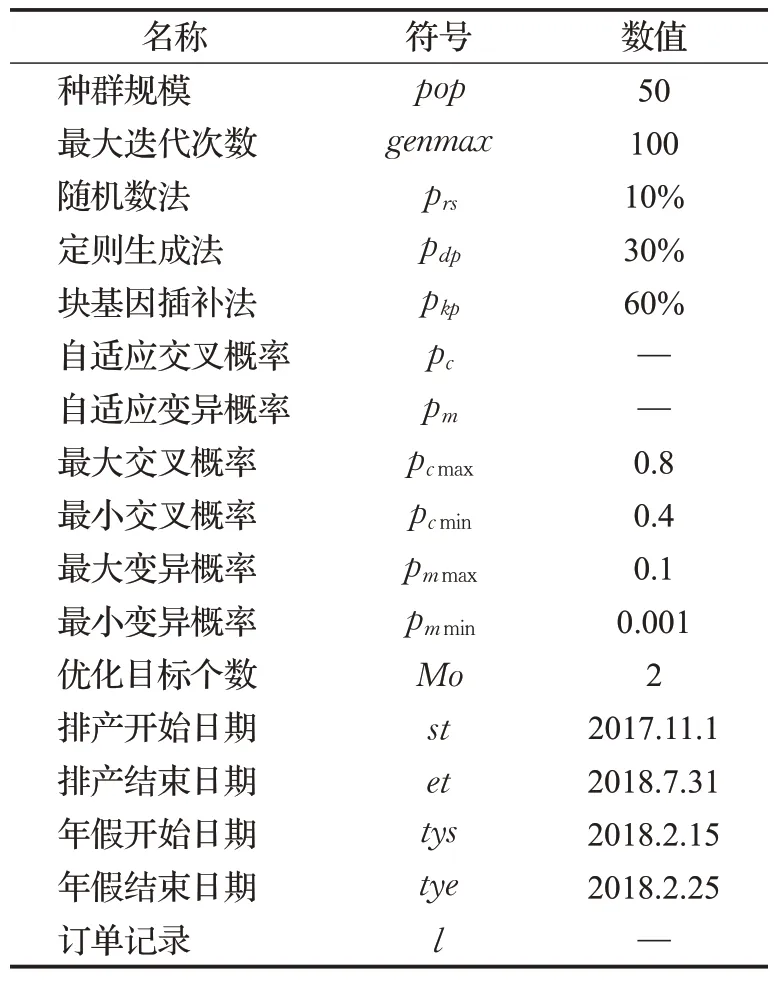
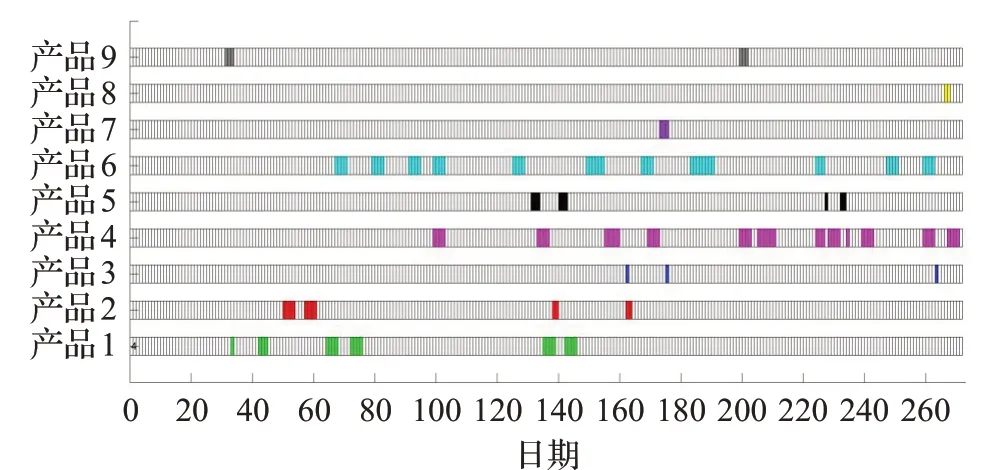
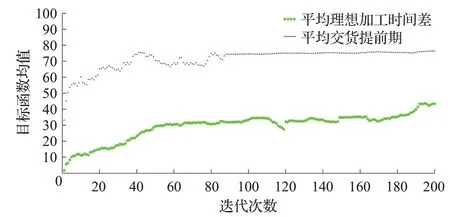
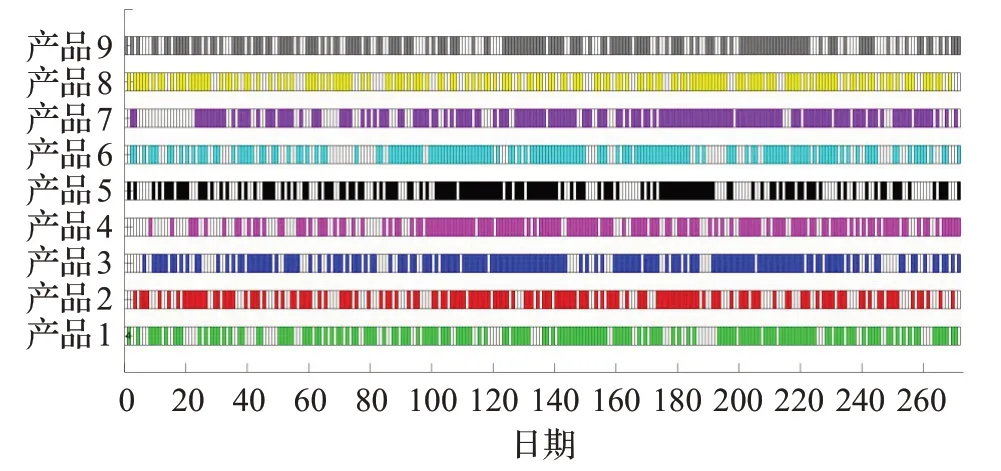
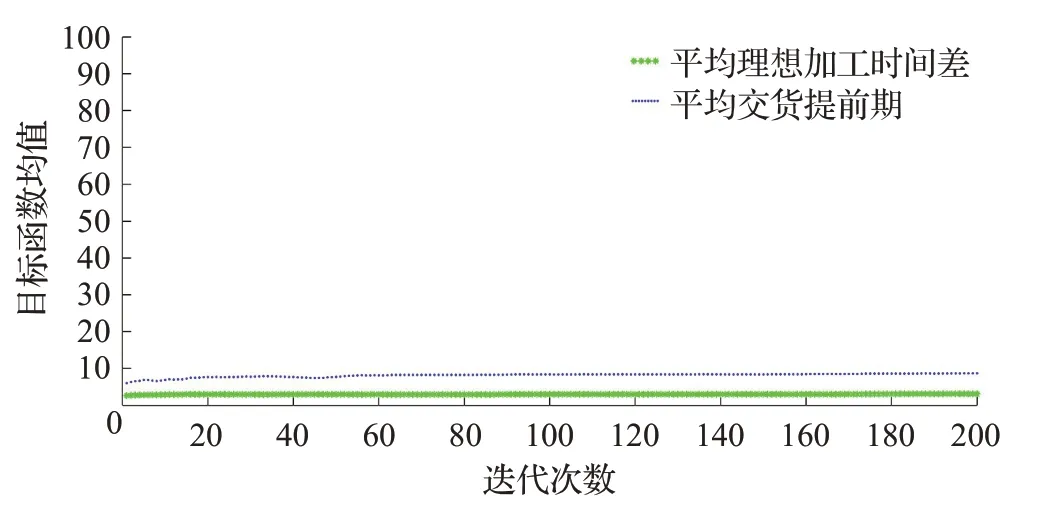
步骤11判断是否达到最大种群迭代次数,作为终止判断条件。如果t 步骤12选择最优第一排挤层作为最优排产结果集进行输出,并随机选取其中一个种群进行可视化展示。 改进NSGA-II算法流程图如图3所示。 图3 基于改进NSGA-II技术的多目标排产算法流程图Fig.3 Flow chart of multi-objective scheduling algorithm based on improved NSGA-II technology 本文以Matlab2014a 做为仿真实验工具,CPU 2.16 GHz,内存为4 GB的计算机作为运行环境,以实际公司车间排产数据为研究对象进行仿真分析。表1 为实际车间排产数据。改进NSGA-II算法的初始化参数表如表2所示。 表1 某公司2018年车间排产数据表Table 1 Workshop scheduling data of a company in 2018 表2 改进NSGA-II算法初始化参数表Table 2 Initialization parameters of improved NSGA-II algorithm 根据仿真实验,分别进行了仿真迭代次数genmax为100、150、200、500 的仿真测试,其仿真结果如图4~7所示。 由图4~7可以看出,仿真结果在100代和200代时,排产效果比较好;在150 代时,排产结果虽然分布比较均衡,但是产品之间重叠比较严重,不太符合产品实际排产需求;在500 代时,排产结果密集程度和重叠程度均比较严重,没有展现实际排产价值,综上所述,仿真结果在100 代和200 代时,其结果是十分具有实际参考应用价值。由图8 可以看出,算法在100 代时,其交货提前期目标函数值基本上收敛,因此确定算法最佳迭代次数为100代,同时也证明了算法的高效性。运用传统NSGA-II算法对其进行相同参数的排产仿真实验,仿真迭代次数genmax 为100 和200,其仿真结果如图9~11所示。 图4 改进NSGA-II算法100代排产GANNT图Fig.4 Improved NSGA-II algorithm GANNT chart of 100 generation production scheduling 图5 改进NSGA-II算法150代排产GANNT图Fig.5 Improved NSGA-II algorithm GANNT chart of 150 generation production scheduling 图6 改进NSGA-II算法200代排产GANNT图Fig.6 Improved NSGA-II algorithm GANNT chart of 200 generation production scheduling 图7 改进NSGA-II算法500代排产GANNT图Fig.7 Improved NSGA-II algorithm GANNT chart of 500 generation production scheduling 图8 改进NSGA-II算法目标函数均值迭代图Fig.8 Improved NSGA-II algorithm iterative graph of mean value of objective function 图9 传统NSGA-II算法100代排产GANNT图Fig.9 Traditional NSGA-II algorithm GANNT chart of 100 generation production scheduling 图10 传统NSGA-II算法200代排产GANNT图Fig.10 Traditional NSGA-II algorithm GANNT chart of 200 generation production scheduling 由图9~11 可以看出,传统的NSGA-II 算法的排产有效性极差,不仅排产安排密度大、偏差远,而且较严重的违背了排产过程中的现实约束,因此,基本上不具备实际应用参考价值。对比图8 和图11 可以看出,改进NSGA-II 算法在目标函数的结果上有明显的优化效果,且能够实现较快速的收敛,证明了算法的有效性和优越性。算法的运行时间在40 s左右,相较繁杂的纯手工排产,可以极大地提高企业的组织效率。因此,本文提出的改进NSGA-II 算法在排产领域具有较好的应用前景。 图11 传统NSGA-II算法目标函数均值迭代图Fig.11 Traditional NSGA-II algorithm iterative graph of mean value of objective function 智能排产技术作为智能化工厂的核心,是智能化发展与实现迫在眉睫的关键技术。本文通过对智能算法NSGA-II的深入研究,发掘NSGA-II算法与排产模型的紧密关联性,同时利用NSGA-II算法自身在搜索寻优方面的强大能力,将其应用于智能排产技术的研究,为智能化工厂快速发展与实现奠定坚实的基础。针对算法的局限性,通过提出改进均匀进化精英保留策略,结合种群个体拥挤度分配对比技术,为每个种群保留多层次的种群个体,解决传统算法多样性差的问题,提高种群解的质量,保留优良基因的传承,避免陷入局部种群最优解;通过对交叉概率和变异概率的重新设计,充分利用种群个体自身的拥挤度特点,为每个种群个体分配相适应的遗传概率,并结合种群的迭代进化而不断的优化,大大地提高了交叉和变异遗传概率的自适应性,解决传统算法在交叉和变异过程中,随机分配遗传概率或者随机指定遗传概率的盲目性,通过结合种群迭代次数以及各代种群个体自身的拥挤度距离,确定适合当前种群个体的自适应交叉概率和变异概率,更好地引导种群搜索寻优的方向,同时加快种群收敛速度。针对排产领域的智能算法研究过程中,基于启发式和元启发式的算法最优先的被应用包括遗传算法、模拟退火算法、蚁群算法等等,改进NSGA-II智能算法是智能排产领域的一个比较新颖的排产算法探索。结果表明改进NASGA-II排产算法,不仅在算法本身的收敛性和种群多样性上有比较好的效果,同时运用于实际的生产排产过程中,能够极大地提高生产排产效率,同时作为公司发布排产的重要参考依据,可以极大地提高公司的生产组织效率和排产智能化的进程。目前,排产优化算法的种类很多,针对不同行业对智能算法的应用研究也十分广泛。本文提出的改进NSGA-II 算法虽然在保留优良个体方面及收敛速度等方面有较大的提高,但是其排产结果应用在实际的企业大型生产调度模型时,仍不能完全准确的完成直接发布式排产与调度。智能排产算法在复杂的生产排产环境中,要完成精准排程与调度,还需要对模型及算法进行更加精确的建设与研究,这也是需要在接下来的研究中重点突破的关键性难题。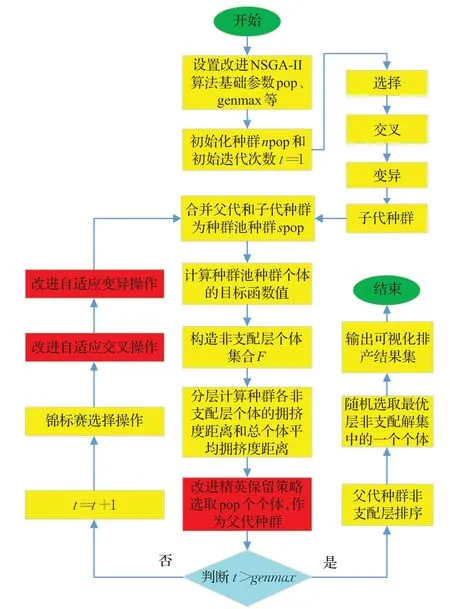
3 改进NSGA-II算法实例




4 结束语

