超声增油用大功率换能器的若干问题
曹志道
(哈尔滨工业大学电子与信息工程学院,哈尔滨,150001)
超声增油工作需要大功率超声换能器,根据增油要求,换能器在水平面内应无方向性,故换能器单元为圆环形;要求设计出的圆环大致能承受1 kW电功率(指脉冲功率,占空比1/5);为了增加增油效能,需要能承受30 kW电功率的超声换能器,因而采用30个换能环并联,结构上各环串装在不锈钢支架上,环间采用耐高温的高约5 mm的聚四氟乙烯环间隔开,换能器串外面再加一个不锈钢管外壳,管内注满硅油,起导声和冷却作用。结构示意图见图1。实测换能器能承受的功率不到5 kW,本文对有关问题作了分析。

图1 超声增油用大功率换能器结构示意图
1 元件参数一致性的要求
通常大功率超声换能器用多个压电陶瓷元件(环)并联构成。若每个元件的功率容量为 P1,则N个元件构成的换能器的功率容量PN=NP1,即增大N倍。实际上由于各元件的参数有一定偏差,这样的理想情况很难实现。我们用压电元件的等效电路来分析[1]。
已知压电陶瓷环的等效电路如图2(a)所示,串联谐振支路为L1、C1、R1,并联静态电容C0。在工作频率附近,可简化为电导G和电纳B的并联,如图 2(b)所示。每个元件上的电压相同,显然等效电导大的元件电功率就大,发热也更高。若各元件的发热量不等,则大功率超声换能器的总功率容量就受发热量最高的元件不烧毁的条件限制。如果能保证各元件的发热功率的偏差不大于 10%,则可保证整个换能器的功率容量不小于0.9NP1。下面我们分析怎样实现这一要求。
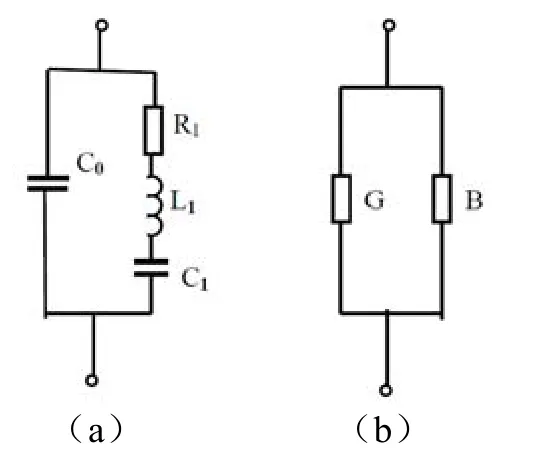
图2 压电元件的等效电路


按式(5)算得的各环发热功率的偏差≤10%,则整个换能器的功率容量的减少也≤10%。
首先讨论电声效率η。实际上1/R1就是压电陶瓷环的串联谐振输入电导,或R1就是压电陶瓷环的谐振输入电阻,R1=R10+R1r(R10为环的损耗电阻,即在空气中测得的数值;R1r为环的等效辐射电阻,它所消耗的电能量就是转变成振动的能量)。R1是在无反射水池中测得的数值。显然,电声效率η为
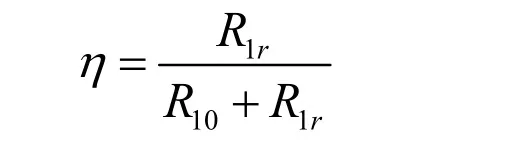
按理,这里的参数值均应为大功率下的测试值,但由于没有足够的环境压力,不能对环施加大的电功率,而且也没有大功率的参数测试设备,所需要的数据无法获得。如果采用小信号数据,则实测电声效率η可达70%~80%。大功率下只能达到30%~40%。本文中假设就用小功率η来控制,或认为η变化不大,暂不讨论η的影响。
其次,讨论R1或其倒数(谐振输入电导),它既包括材料的内部损耗的影响,也包括机电耦合系数的影响,制造过程中会有一定离散度。由式(5)可见,它的相对变化等于环所得电功率的相对变化,也等于发热功率的相对变化。它的离散度决定于制造工艺,假设同一批产品是一致的,本文也不予讨论。
最后讨论谐振频率f0变化的影响。这是环制作完成后可以选择的参数。f0和环的几何尺寸有关,也和材料的配方、工艺和机械性能有关,很难保证参数的一致。换能器工作时,只能用一个频率工作,因此有些环实际上工作在失谐状态。由式(3)~(4)可见,失谐直接影响输入电导,即影响输入电功率。失谐会降低输入电导。Q值不同时,失谐对输入电导的影响也不同。表 1给出了不同Q值下,不同相对失谐量Δf/f0时的输入电导的相对值(以谐振输入电导为基准)。

表1 输入电导随品质因数和失谐量的变化
有载品质因数Q值可从换能环在无反射水池中所测出的导纳曲线推算出来[1],按式(4),当X=1时,输入电导下降为谐振时的一半,由电导曲线查出f0和失谐量Δf0,则
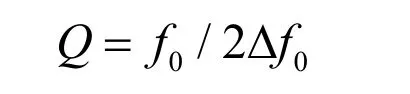
需要注意的是环式换能器的电导曲线实际上是多峰的(拼镶式换能器的曲线较好),频率较高处的峰代表高次振动模式。为了避开高次振动模式的输入电导对基本模式输入电导的影响,测量输入电导下降到一半的失谐量时,宜只取频率偏低方向的数值。限于条件,我们只有整个换能器数据,可能已受各环频率参差的影响,测算出的Q值在6~8之间,单个环的Q值可能还要高。
若分选换能环时,允许环的谐振输入电导的相对变化为5%,则允许失谐引入的输入电导的相对变化也仅为5%。由表1可见,允许的范围为次粗线以上范围,当Q=7时,允许的频率误差仅为1.6%。若同一批环的谐振输入电导有较高的一致性,则可把发热功率不一致的误差因素都给失谐,则表 1允许的范围为粗线以上(除了 3个情况不能用外,其余都能用)。但允许失谐量也仅 2%或稍高。
由以上分析可见,大功率超声换能器组装时,对元件参数一致性应有较高的要求,否则就会减小整个换能器的功率容量。上文估算的一大困难是所有计算中的参数均应采用大功率(因而也是高温下)的参数,但很难获得。采用低功率测得的参数对大功率条件是否适用,用低功率参数分选比不分选是否能好一些。这些问题需要在实践中观察。另外,实际测试发现,预应力会影响换能环的谐振频率和输入电导。加预应力换能环的参数分选应在加预应力之后进行。
对拼镶式环来说,参数一致性问题更大(如一个环由20片构成,各片参数不一致就会出问题),也更不好测量(各片间强耦合,测量时应同时加信号,但只测某一片的参数)。
综上所述,提高环的生产工艺水平,可以保证环的参数一致性,否则就得用大量测量来分选换能环。
2 换能器的传热学问题
增油用换能器的平均功率大,因而发热也多,散热是重大问题。环境温度随油层的深度而变,大致是每深入100 m地温升高3.3 ℃,4000 m处则已超过130 ℃,这温度已是压电陶瓷工作的温度极限。对于整个换能器的散热问题,有几部分热阻起作用:环内部到环表面(发热和传热介质都是陶瓷,外表面可能有加预应力的玻璃钢,也会有热阻),环表面到换能器壳的内表面(传热介质是硅油,对流和传导都起作用),再传导到换能器壳的外表面(壳是不锈钢制成,靠传导散热)。下面根据传热学理论计算相应的热阻[2]。
2.1 外壳的热阻
根据传热学,材料的传热能力和材料的传热面积S(垂直于传热途径)成正比,和传热途径的长度D(即材料的厚度)成反比,和两面的温差t成正比。即材料所能传导的热功率P为:

式中,α为材料的导热系数,可由手册查出。由此,热阻(即传导1 W热功率所需要的温差)Rr为

设换能器外壳厚度D=1 mm=0.001 m,外壳直径d=62 mm=0.062 m,外壳高H=1.15 m,故传热面积S= πdH=π×0.062×1.15= 0.224 m2,对不锈钢,α=15 W/m℃,故外壳的热阻为
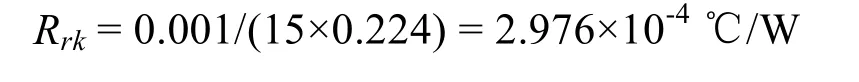
如改用黄铜,它的导热系数α=109 W/m℃,则热阻为 4.096×10-5℃/W。
2.2 压电陶瓷环的发热和传热
压电陶瓷环的情况较复杂, 既是热源又是传热介质。按传热学的分类,这属于有内热源的情况。现分两种情况来讨论。
(1)设环的两侧都是传热很好的液体时发热的总量同时从两侧散出。为分析简单起见,认为环很薄,两侧面可看作平行平面,如图3所示。
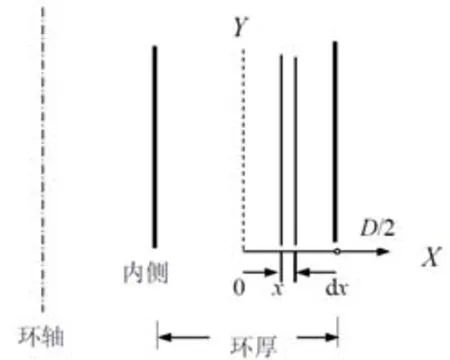
图3 压电陶瓷环的发热和散热
设环的壁厚为D,考虑到对称,分析时取一半就可,在环厚一半处取Y轴。Y轴右侧环体产生的热量需从环外侧散出,左侧环体产生的热量需从环内侧散出。在x处取厚为dx的薄层,0~x范围中压电陶瓷的发热量都需通过dx层传出,故dx层两边的温差为dt。

举例,已知压电陶瓷的α=2.1 W/m℃,环的尺寸为 Φ47×Φ33×32 mm,即壁厚D=7 mm=0.007 m。若要求30个环组成的换能器的功率容量能达到30 kW,则每个环的功率容量应为1 kW(指脉冲功率,当占空比为1:5时,平均功率为200 W)。按电声效率为30%计算,则每个环的平均发热功率为140 W。故单位体积发热功率σ为:
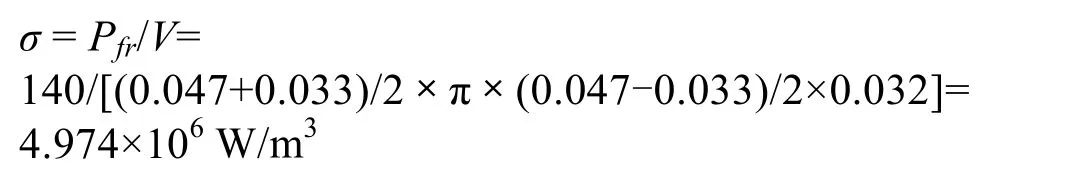
故按式(8)可算得环中心温度比环表面温度:
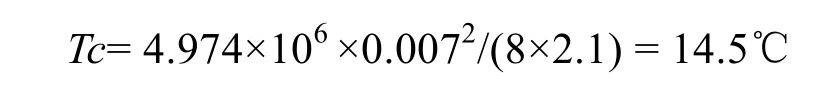
环外包上玻璃钢以对环施加预应力,其厚度为1 mm,导热系数和陶瓷相同,则D=8 mm,玻璃钢两边温差为4.4 ℃,此时环中心比环表面的温度差增加为18.9 ℃。

把具体数据代入,可算得单个环的热阻为0.103 6 ℃/W。对整个换能器来说,30个环的热阻也是并联的,故环的总热阻为 3.453×10-3℃/W。与上节结果相比,可见环的热阻是不锈钢外壳热阻的11.6倍,是黄铜外壳热阻的84.3倍。由此看来外壳改用黄铜的意义不大。
(2)若环内侧的硅油是封闭的,不能很好地把热量传导到外壳散热,不论内部有多少油量(油多只是时间常数大,即温度稳定的过程长),只要和外部没有散热通路,全部热量只能通过外表面散出,则问题变得非常严重。
原先环产生的热量往两侧传播,现在只往一侧传播,故要传播的热量加大了一倍。环的体积没变,故单位体积产生的热量也不变,但温度分布却变化了,外侧温度仍最低,而内侧的温度最高,相当于把图3中的Y轴移到内侧,传播途径加大了一倍。这样内外侧的温差就加大到4倍。即58 ℃。通过玻璃钢层的热量加大一倍,故温差增为8.8 ℃,玻璃钢层外为66.8 ℃。可见如何改善环内侧的散热条件是非常值得研究的问题。
2.3 传热液体的热阻问题
考虑到换能器中有振幅很大的超声振动,液体的流动方式可能主要是紊流,对散热有利,但对此如何计算,尚未掌握,有待进一步研究。在以下的讨论中设液体的热阻很小,不考虑。
3 工作环境温度的影响
根据热阻的概念,系统能散出去的热功率限制了系统可加的电功率。而系统能散出去的功率正比于温度差。已知压电陶瓷的允许工作温度为120~130 ℃,若环境温度(换能器处理时需对准油层,故环境温度也就是相应地层中的温度)为40 ℃(海面温度),则温差为80~90 ℃,设可加功率为Pm。当油层位于2500 m深处时,环境温度可超过80 ℃,温差仅为 40~50 ℃,显然允许功率降为Pm/2。到4000 m深时,环境温度高达130 ℃,显然压电陶瓷换能器根本无法使用。采用“热采”技术的稠油井,采油前通入温度高达 280 ℃的高压蒸气,待地层温度升高,油的流动性改善后,才能开始采油,显然压电陶瓷换能器在这里也无法使用。
我们来计算井深对换能器工作容量的影响。设换能器的材料允许工作温度为 130 ℃。换能器原以海面最高温度为40 ℃设计,采用玻璃钢加预应力,环内侧封闭,即单侧散热,允许电功率为Pm。以下计算设换能器不发生电击穿,或去极化。只是从散热设计来考虑。
表2中第一列是散热条件和内部温升。第一行是油井深和地层温度。计算方法:设油井深为1000 m,基本状态(即额定功率下)第一种散热条件下,换能器内外侧温差为66.8 ℃,按前述不计硅油和不锈钢外壳的热阻,外侧温度就是环境温度33 ℃,环内侧最高温度为33+66.8=99.8 ℃,工作无问题。若加大输入电功率(只考虑温升限制,不考虑电击穿)使环内侧最高温度达到 130 ℃,则功率可加大到(130~99.8) /66.8=45%,即功率可加大为原有的1.45倍。若井深3000 m,地温99 ℃,则换能器满载时表面温度已达99+66.8=165.8 ℃>130 ℃,需降额使用。计算可得需降到半额以下。这里就认为不可用了。如不包玻璃钢,则满额时表面温度为99+58=157 ℃>130 ℃,需降额使用。已知58 ℃是满额温升,故需降(157-130)/58=47%。
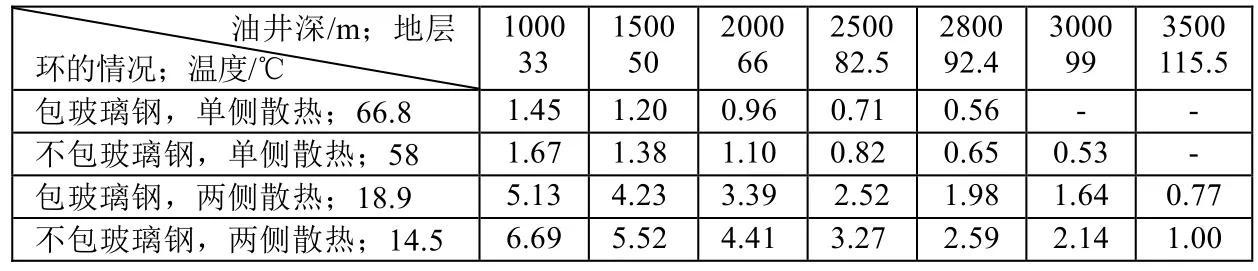
表2 允许电功率与额定功率的比和油层深度关系
由表2可见,改善环的散热条件非常重要,不宜包玻璃钢,尤其是必须改善内侧散热。满足这一条件后,可能研制出用于3000 m油层的换能器。但要达到4000 m深度是不可能的。为了超声增油技术能用于深井或热采油井,只有采用居里点温度较高的(1100 ℃)LiNbO3材料来制作换能器。
实际上设计时,已有较大功率裕量,按环的尺寸为 Φ47×Φ33×32 mm,故体积为 28.1 cm3,工作频率为27.3 kHz,若考虑采用1.5 W/(kHz·cm3),则每环可加功率为1.152 kW。考虑脉冲工作,裕量更大(前面从散热角度的分析已考虑了脉冲工作)。但实际却承担不了0.27 kW(约工作在1800 m深的油井)。
上述分析发现的主要问题是散热设计不够合理,尤其是内侧的散热。
4 多元件之间的声耦合引起的振动模式
换能环的设计所采用的压电效应是:沿圆环的厚度(或称圆环的径向)加电场,而变形则是沿环的圆周方向(或称切向),也就是利用了d31(拼镶式环的电场方向和变形方向一致,即利用 d33,数值大,有利)。实际上,沿环的高度方向也是有变形的(也是d31),只是高度(32 mm)没有环的平均周长(125.7 mm)长, 因而高度方向的谐振频率要高得多,以避免高度振动的影响。这是设计环尺寸主要考虑的问题。但从元件组合来看,各环的高度方向是通过聚四氟乙烯环(高度为5 mm)隔开的,但换能环和聚四氟乙烯环密切接触,而聚四氟乙烯是较好的导声体。这使得各环沿高度方向的振动有很强的耦合。环柱高度为30×(32+5)-5(聚四氟乙烯环只有29个)=1105 mm,内外径分别为33 mm和47 mm。这样高度比平均周长大得多,那么高度方向的谐振频率会低得多,也远离平均周长的谐振频率(工作频率)。但高度方向的高次模式可能进入工作频率附近而影响工作。
我们提出两种解决方案:一是改变聚四氟乙烯环的形状,使换能环间的接触面积尽量减少,以减少声耦合;二是考虑到高度方向的振动不是这种换能器的工作模式,可把环间的聚四氟乙烯环改为吸收性好的材料,如加入铅粉或钨粉等。这还可能进一步降低环的 Q值,放宽对参数一致性的要求。
5 结论
本文对超声增油大功率换能器的生产问题作了理论研究,认为对所用环要做较严格的分选,结构上对散热问题需加以重视,防止环间的寄生耦合。另外,整个增油系统还有很多问题需要研究,本文无法全部涉及,如整个换能器的静态电容随环境温度变化而变化较大,对电路有较大影响;电缆长度和震动波长相近因而电路计算应按分布参数考虑等,有些还和整个结构有关。作了相关改进后,换能器整体的性能有较大的改善。换能器的功率容量大致提高了2~3倍。

