基于FAHP的城市轨道交通运营指标分析

陈建球 庞彦知

摘 要：城市轨道交通的快速发展，在保证地铁运行安全的基础上，提高运营服务质量，提升运营效益也被日益提上日程。本文综合专家评价信息的主观不确定性和模糊性的特点，运用三角模糊层次分析法和专家咨询法确定指标的权重。首先通过全面分析运营指标评价影响因素，构建运营指标评价体系。并对各个指标进行综合分析，确定最终指标并建立较为综合且不失针对性的运营指标评价体系;然后利用三角模糊数计算权重，得到重要度排序。最后通过南宁地铁1号线实例验证，确定通过三角模糊层次分析法构建的运营指标评价体系的可行性。

关键词：专家咨询法;三角模糊层次分析法;运营指标体系

1 城市轨道交通运营指标

城市轨道交通运营指标的选择具有系统性、客观性、可比性和可操作性。而评价体系的最终目的是以此来辅助城市轨道交通管理者的工作，实现对轨道交通向更合理的方向运营提供指引，为相应的管理者做决策提供一定的参考，并可实现对改进措施实施后的效果进行反馈。因此选取合适的运营指标，构建评价体系对城市轨道交通运营效益进行分析成为迫切需求。

2 基于FAHP的城市轨道交通运营指标评价体系建模

在应用传统的层次分析法进行计算时，由于人的判断具有模糊性，会出现判断结果差异较大的情况。而FAHP方法兼顾了两者的优势，在专家打分的时候引入模糊数，使打分更加准确。为了更好的选出评价指标，分析相关因素对运营的影响，需总结并列出初选评价指标体系。评价体系的建立包括两个阶段，初级评估阶段和筛选阶段。

2.1 评价指标

2.1.1 线网结构指标

（1）线路长度C11：为满足轨道交通出行需要铺设的线路长度。（2）车站数量C12：即轨道线路上设立的乘车站点数量。（3）换乘选择比C13：衡量采用轨道出行方式的可直达性程度。

2.1.2 数量指标

（1）客运量C21：是指在一定时期内运送的全部乘客数。（2）客运周转量C22：反映旅客总的走行距离。与轨道交通的客流数量、覆盖范围、运营成本等指标密切相关。（3）客运密度C23：反映运输线路的繁忙程度。（4）满载率C24：用以表示车辆的利用程度，同时在一定程度上也可反映运营效益。

2.1.3 质量指标

（1）车辆数量C31：投入营运的车辆数。（2）安全性效益C32：一定时期内，旅客发生事故次数与旅客周转量之比。不仅关系到乘客的人身安全，还体现了良好的城市形象。（3）顾客满意度C33：通过感到满意的乘客人数占抽样调查乘客总人数的百分比来判断。（4）节约时间效益C34：出行时，乘坐轨道交通方式與其他交通方式相比，差额时间即为节约时间，这部分时间可以用来创造社会价值。（5）单位运营成本C35：该指标表示每位乘客的平均运营成本。该指标可以显著反映地铁公司的投入产出效益，反映运营公司在成本管理方面的成效。

2.2 评价指标体系框架的构建

根据城市轨道交通运营指标确定的层次结构模型，线网结构指标、数量指标和质量指标作为准则层，车站数量、线路长度、换乘选择比是线网结构指标的指标层，客运量、客运周转量、客运密度、满载率是准则层数量指标的指标层，车辆数量、安全性效益、顾客满意度、节约时间效益、单位运营成本是准则层质量指标的指标层。对指标进行了筛选，去除了不可靠的评价指标，同时为了保证指标的含义、计算步骤具有正确性，建立如图1所示体系框架。

3 实例验证

选取南宁地铁1号线数据对模型进行验证。

3.1 评价指标体系权重的确定

3.1.1 构造互补判断矩阵

本文邀请三位专家（包括教授、工程师等，他们来自不同的部门，代表了对轨道运营认识的不同视角）进行打分，对同一层次的指标进行两两重要性比较，给出所认为的最悲观值、最可能值、最乐观值。打分用模糊数（lij，mij，sij）表示，当lij=mij=sij时，则是一个精确数。

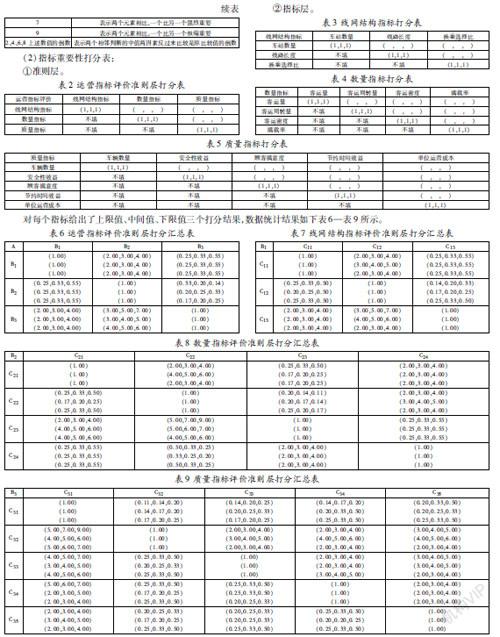
（1）指标标度方法如下表1：

对每个指标给出了上限值、中间值、下限值三个打分结果，数据统计结果如下表6—表9所示。

数据选取的原则如下：

a.当专家打分的平均值为非1～9标度值，如3.6或者5.3，则取近似值为4和5。

b.当专家打分的值sl大于3，则认为其不合理，剔除之后重新赋值。

c.当专家的打分出现矛盾时，例如专家一打分为（3，4，5），专家二打分为（1/5，1/4，1/3）时，则专家进行该指标的讨论，重新打分。

对准则层B的三个指标构造的判断矩阵如下表10所示：

同理，对准则层下的C层各指标进行两两比较，构造了模糊判断矩阵，结果见表11、表12、表13所示：

3.1.2 层次单排序

下面主要以B层指标相对于A层权重的计算过程为例，进行详细计算。具体步骤如下：

（1）模糊矩阵的各行元素的算术平均值。

根据三角模糊数的公式aij=（r1ij+r2ij+…+rtij）/t得出：

w1=∑3j=1a1j3=1+3+133=1.443

计算结果如下：

w～=[w1，w2，w3]T=[1.443，0.510，3.000]T

（2）将w～进行归一化处理，得到B层各因素相对于A层的权重。

w～=[0.2583，0.1047，0.6370]T