Improved analysis of the rare decay processes of Λb
Ren-hao Deng, Yong-lu Liu and Ming-qiu Huang
College of Art and Science, National University of Defense Technology, Hunan 410073, China
Abstract It is noted that in the new Particle Data Group (PDG) version the rare decays of the Lb baryon have been revised with more accuracy.The new results show that most of the existing theoretical results on the process L b →Lγare larger than those of experiments.With the improved higherorder light-cone distribution amplitudes of the Λ baryon, we reanalyze the process in the framework of light-cone quantum chromodynamics sum rules and the branching ratio is estimated to be Br (L b →Lγ) = (7 .38 ×10-6, which is consistent with the new experimental result.Furthermore, another process L b →L l +l -is also analyzed in the same frame.The final branching ratio is calculated to be Br (L b→Ll +l -) = 1.20 ×10-6,which is in good accordance with the data from the PDG and other theoretical predictions.
Keywords: light-cone distribution amplitude, rare decay, light-cone QCD sum rules
1.Introduction
The flavor changed process of the heavy hadron is a pure platform for studying information on the internal dynamics of the hadron, which is important for investigations of the properties of the strong interaction both at quark level and hadron level.The rare decay of the heavy b-hadron,which is forbidden at the tree level in the standard model (SM), is related to the flavor changing neutral current (FCNC).The loop of a virtual quark and a boson component dominates the process,so we can analyze the element of the Cabibbo–Kobayashi–Maskawa(CKM) matrix about Vtsand Vtb[1] more accurately, which may provide information on new physics beyond the SM.
In the past 30 years, many experimental and theoretical efforts have been devoted to this topic,especially in the sector of meson decays[2–7].The rare radiative B meson decay was seen for the first time early in 1993 by CLEO.With the observation of the processB→K*γ, a lot of experimental data have been accumulated and increasingly exact measurements of inclusive and exclusive branches have been reported [8–10].Theoretically, different methods have been used to investigate the processes of theb→sγsection within and outside the SM [11, 12].The theoretical predicted decay rates of the inclusive processes are well in agreement with experiments.However,the exclusive process of B-meson rare decay needs to be improved, since it is associated with nonperturbative contributions.
In comparison with processes of the B-meson, the rare decay of the b-baryon has received little attention due to its complex quark contents,and the experimental data are also not sufficient for further theoretical study [1].Simultaneously, the process of b-baryon decay can help us learn more about the quark information inside hadrons, such as processes of hadronization and the hadron spin polarization.The hadronization process of b-quark supplies a new window for studying of the exclusive rare radiative Lbdecays, which have been employed in many processes with the quark model [13–16], quantum chromodynamics (QCD) sum rules [17] and the QCD perturbative method[18].Nevertheless,there are many differences in theory, even in order of magnitude.The processes of the rare decays Lb→Lγand Lb→Ll+l-have been studied with light-cone QCD sum rules (LCSR) [19–22].Nevertheless,recent experimental data show that most of the existing theoretical results are much larger than those expected.Therefore,it is instructive to reanalyze these processes.
In the LCSR method the most likely error may come from the higher-order corrections of the light-cone distribution amplitudes (LCDAs).In previous work [23–32], the LCDAs of Λ have been renewed considering corrections from higher-order conformal spin expansion.This indicates that this correction may provide a contribution to the processes.Another uncertainty originates from the interpolating current of the baryon, which has been shown in the calculations of electromagnetic form factors [33–35].The improvement of the current work is to use the renewed LCDAs to reanalyze the form factors related to the two rare decay processes.It is expected to give more reliable predictions which can be compared with the new experiments.
The presentation is organized as follows.Section 2 is devoted to introducing the theoretical framework of the decay processes.In section 3 we give form factors with LCSR in next to leading order(NLO)of the LCDAs using two types of interpolating currents.The numerical analysis is presented in section 4, in which the dipole formula is used to fit the form factors from LCSR.Finally, the summary and conclusion are presented in section 5.
2.Theoretical framework
In the SM, the effective Hamiltonian of the processes Lb→Lγand Lb→Ll+l-atμ=O(mb) [36, 37] are expressed as
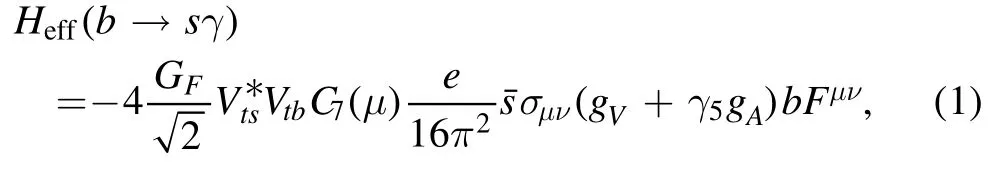
and
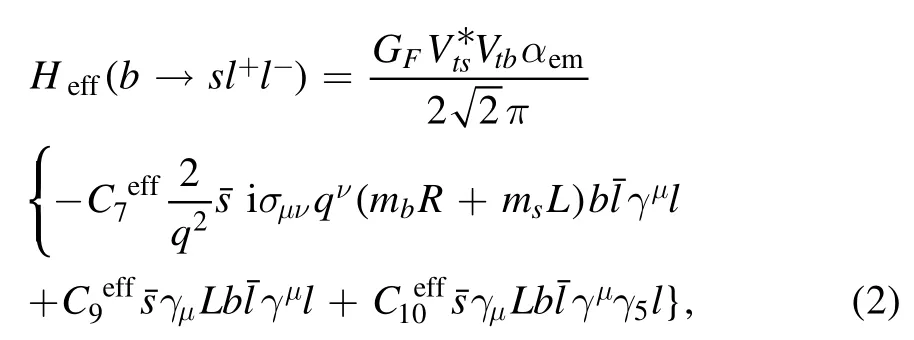
where GFis the Fermi coupling constant,andare Wilson coefficients at μ.
The hadronic parts of the processes are dominated by the nonperturbative effects at the quark level, which can be parameterized with the form factors defined by the matrix elements of the interaction currents between the initial and final states:
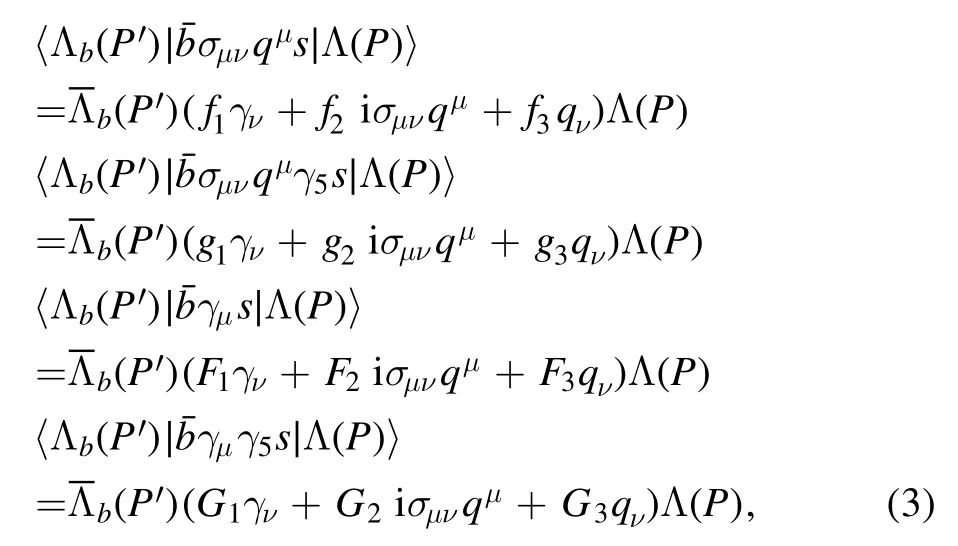
where Lband Λ are the spinors of the Lband Λ baryons respectively,P′ =P+qis the momentum of Lb,and q is the momentum transfer.
The final states of Lb→Lγcontain a real photon,which makes the sector of hadron parameterization simpler:

The decay rate of of this process is expressed with the form factors as
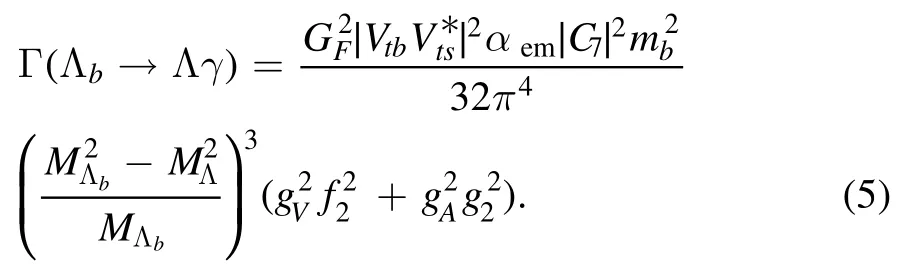
For the process Lb→Ll+l-, the differential decay width on q2is expressed with form factors as follows [21]:

In order to calculate these decay rates, we need to evaluate all the form factors that appear in the equation.Due to the nonperturbative properties of QCD at hadron level, we should use some nonperturbative methods when calculating these parameters.Herein, the LCSR are adopted to calculate various form factors.
3.Light-cone sum rules of the form factors
The main idea of the QCD sum rule method is to calculate the correlation function from both the hadron level and the quark level.However, the description of the hadron with quarks relies on the model of how we construct the interaction between them.Usually the interpolating current are used to couple to the hadron.Nevertheless, the choice of the interpolating current is not usually definite, especially for multiquark states.
The criterion of the choice about the interpolating current is that it couples strongly enough to the hadron.In the following analysis of the LCSR, we use CZ-type and Ioffe-type currents respectively for a comparison [38–40].The CZ current is
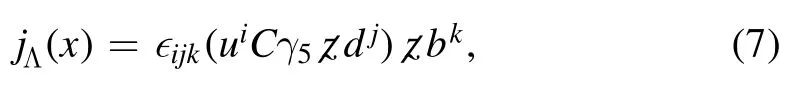
and the Ioffe current [41–43, 40] is
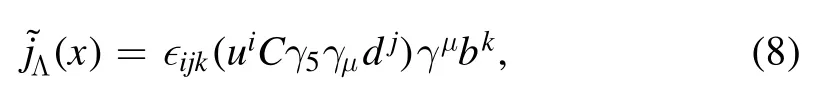
where C is the charge conjugation matrix,i,j,kare the color indices,and the auxiliary four-vectorμzis a light-cone vector which satisfies the conditionz2=0.The coupling coefficients of interpolating currents to the hadron are defined by the matrix elements of the currents between the vacuum and Lbbaryon state

and
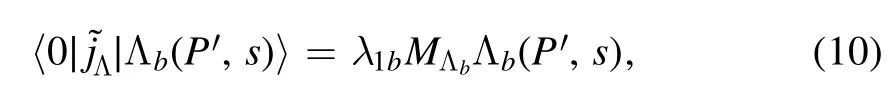
whereP′ is the momentum of Lband s is its spin.
The LCSR start from the correction function

where q is the momentum transfer.
The hadron part of the process Lb→Lγcan be parameterized as the form factors defined by the matrix elements of the interaction currentbetween the Lbstate and Λ state:
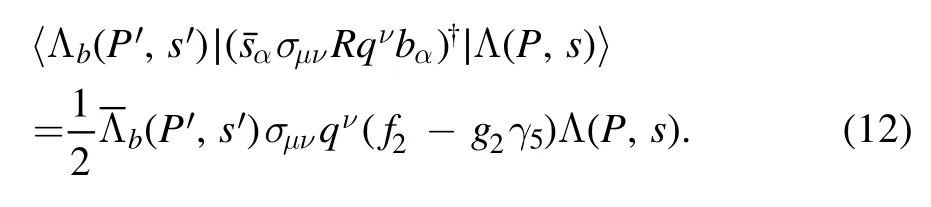
By interpolating a complete set of intermediate states with the same quantum numbers as the initial state in the correction function, we obtain the hadronic representation
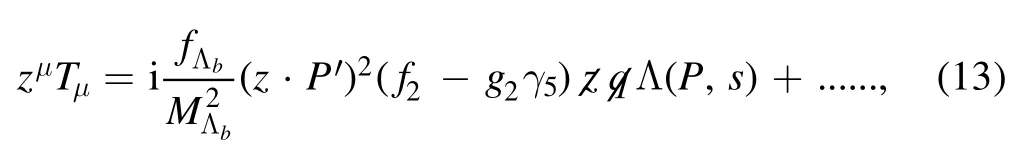
in whichP′ =P-q, and the dots represent contributions from higher resonance and continuum states.Herein the lightcone vectorzμis used to contract the correction function and simplify the Lorentz structure in LCSR, so that contribution terms on the light-cone dominate in the processes [20, 44].
On the other hand, the correction function can be expanded on the light-cone.We can contract the b quark to calculate the correlation function at the quark level to the lead-order ofαsas:
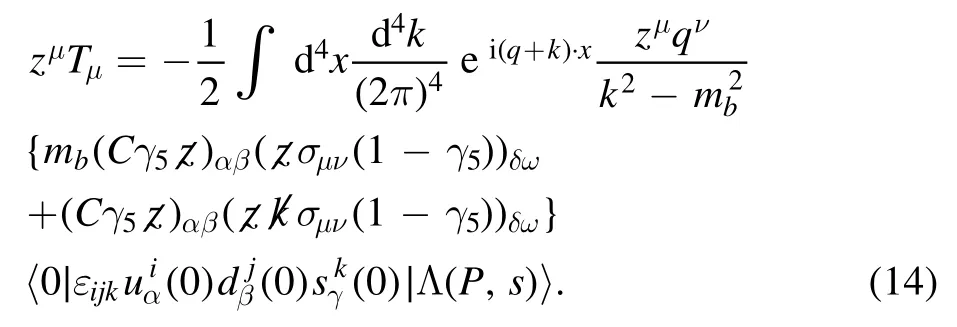
The nonperturbation effects can be calculated by the construction of nonlocal matrix elements between the vacuum and the Λ baryon state, which are usually parameterized as LCDAs.
With the standard procedure of LCSR, the two sides are matched, and the higher resonance contributions on the hadronic side can be expressed by the quark level with the assumption of quark–hadron duality.Hereafter, the Borel transformation is applied to suppress contributions from both the higher resonance and higher twist LCDAs.We arrive at the sum rules of form factors f1,f2,F1and F2,which is shown explicitly in appendix A.As for form factors g1, g2, G1and G2,we can obtain them from the relationsg1= -f1,g2=f2,G1=-F1andG2=F2.
A similar result can be obtained with the replacement of the interpolating current by the Ioffe-type oneThe sum rules are shown in appendix A.
4.Numerical analysis
Before numerical analysis, some inputs need to be determined.In order to reduce the uncertainty from the sum rules itself,we choose values of the coupling constants as obtained from QCD sum rules.The results arefLb= (3.86±0.13) × 10-3GeV2andλ1b=(0.027 ±0.03) GeV2[34].Other parameters can be chosen from the Particle Data Group(PDG)asMLb=5.62 GeV,ML=1.116 GeV,and the b quark mass ismb=4.7 GeV [19, 21].The distribution amplitudes are the most important input parameters in LCSR.Hereafter, we use the renewed results which have considered effects from higher-order conformal spin expansion [23, 29,45].For the completeness of the text, we list the LCDAs in appendix B.
The most important auxiliary parameters in LCSR are the threshold s0and the Borel massSince the threshold is the parameter that is chosen to ensure that the integration of the spectral density upon it is equivalent to contributions from higher resonances, it is usually connected with the first excited state with the same quantum numbers as the ground state.Herein we choose the threshold in the region 39 GeV2≤s0≤41 GeV2.Meanwhile, the choice of the Borel parameter should meet the requirement that both higher twist contributions and higher resonance contributions are suppressed simultaneously.With the simulation, we acquire the appropriate range ofas 18 GeV2≤≤22 GeV2,which is the Borel window adopted in the next analysis.It is noticed that the Borel window is different from that in the previous work, 10 GeV2≤≤15 GeV2[21].The reason lies in the fact that the convergence of higher twist make it more reasonable to choose the present region, which comes from influences of higher-order corrections of LCDAs.
With the above choices of parameters,we obtain the form factorf2(0) of CZ-type current and form factorsf2(0) andg2(0)of Ioffe-type current.We plot the form factorf2(0)within figure 1 as an example.It is seen that in the region the sum rules are not sensitive to the parameterWe can choose a special value=20 GeV2in the Borel parameter window, in which the higher resonance contribution can be suppressed under 30%.The dependence of the form factors with the momentum transfer is plotted in figure 2 for CZ-type current and figure 3 for Ioffe-type current.
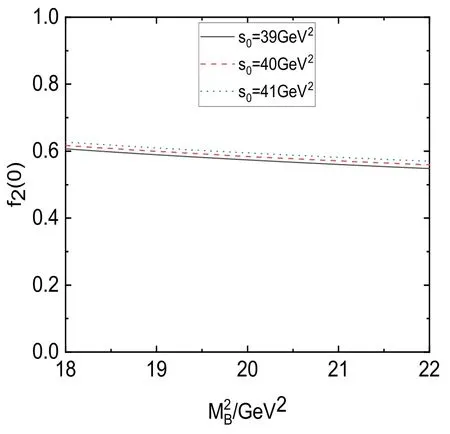
Figure 1.Dependence of form factors f2 (0) on the Borel parameter atq2=0GeV2.
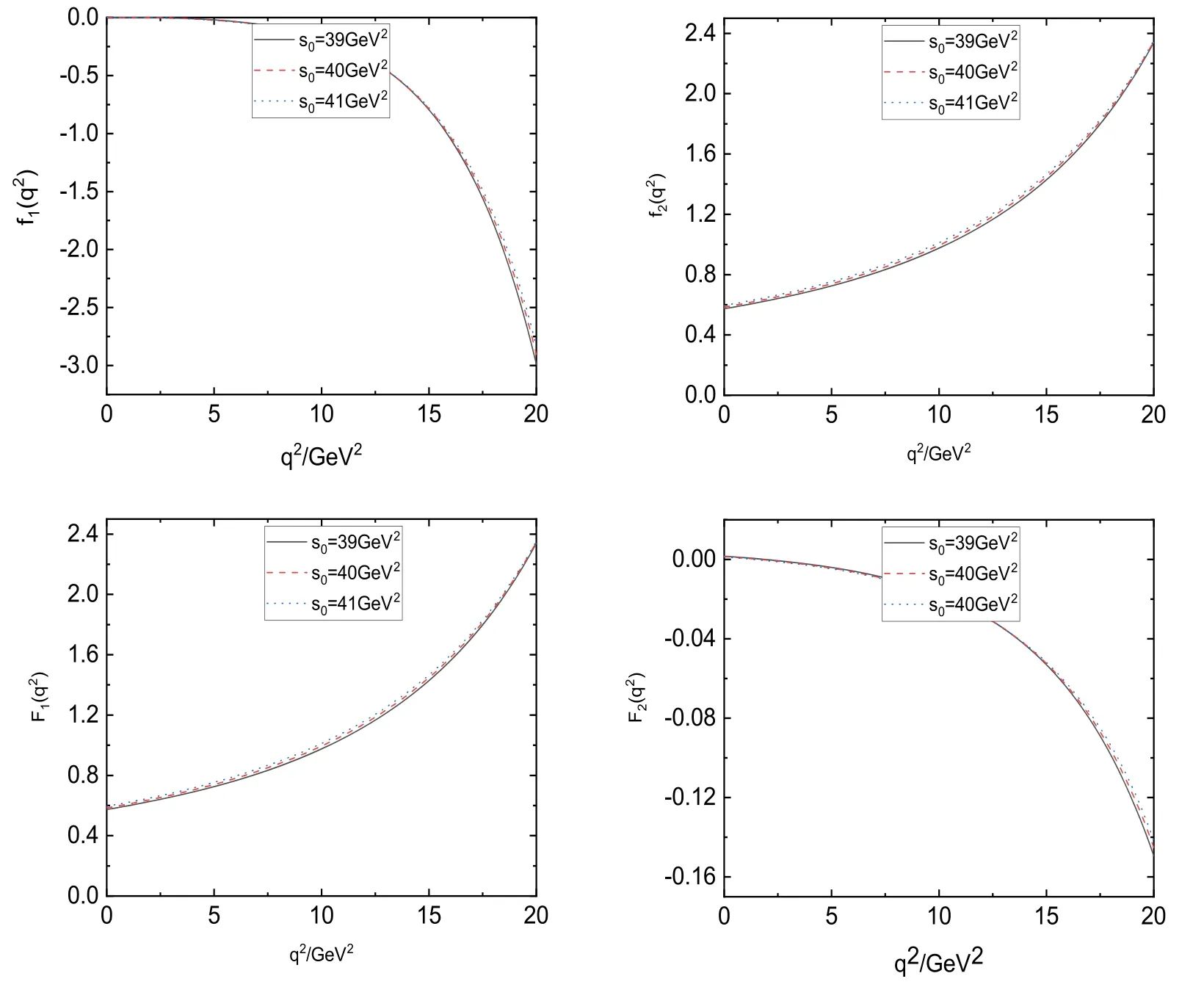
Figure 2.Form factors on the momentum transfer q2 with the CZ-type current.
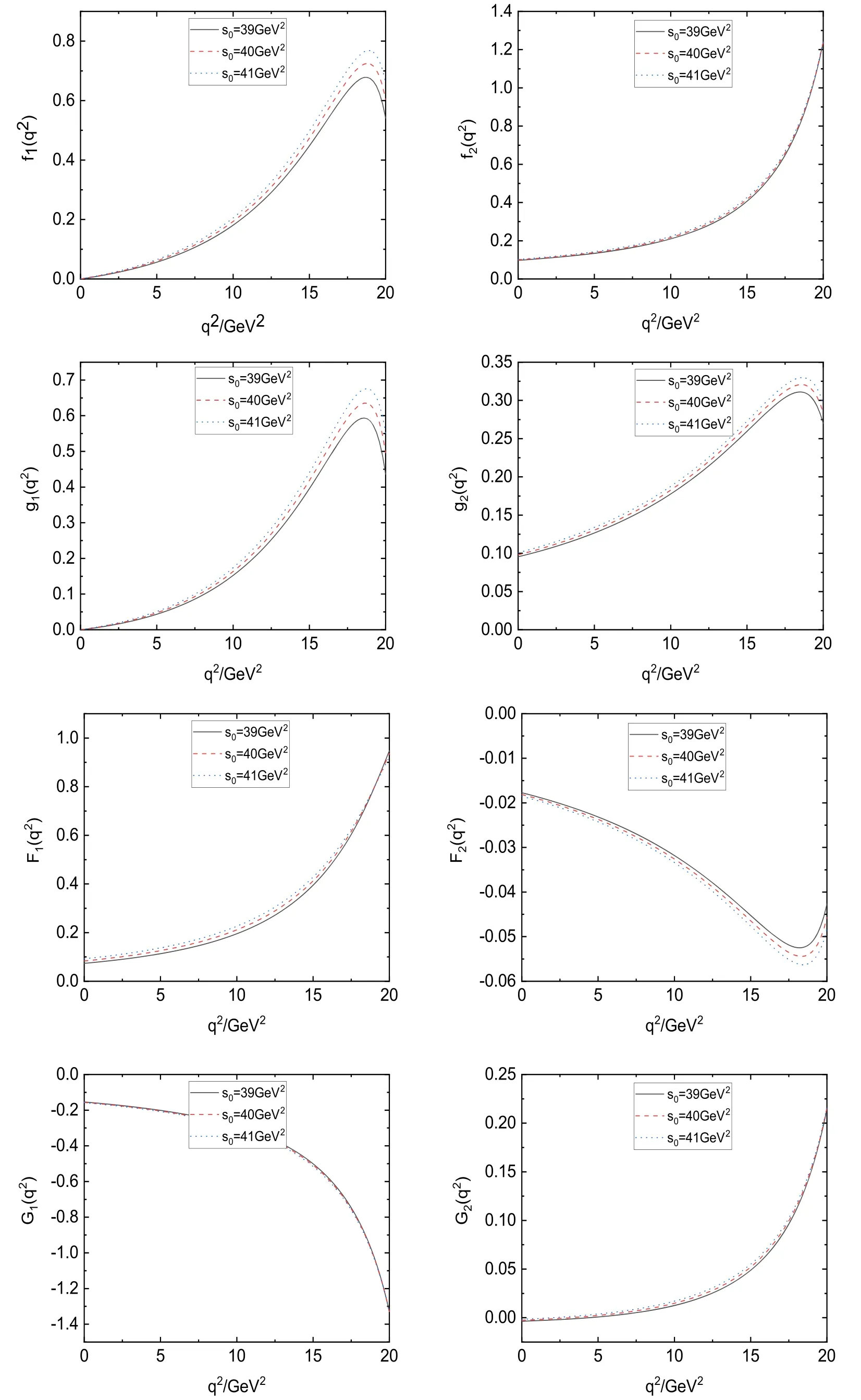
Figure 3.Form factors on the momentum transfer q2 with the Ioffe-type current.
Since form factors from the LCSR are only applicable in the middle momentum transfer, we need to extrapolate the results to the whole dynamical region to obtain the transition information.Herein we use the dipole formula to fit the form factors

where a1, a2andfi(0) have been listed in table 1.It is noted that there are relationsg1= -f1,g2=f2,G1= -F1andG2=F2for CZ-type current.The same results of parameters a1,a2,andfi(0)for the Ioffe-type current are listed in table 2.In the numerical analysis only uncertainties from different choices of the threshold s0and the Borel parameter are considered.

Table 1.Fitted parameters of form factors by the formula (15) with CZ-type current.
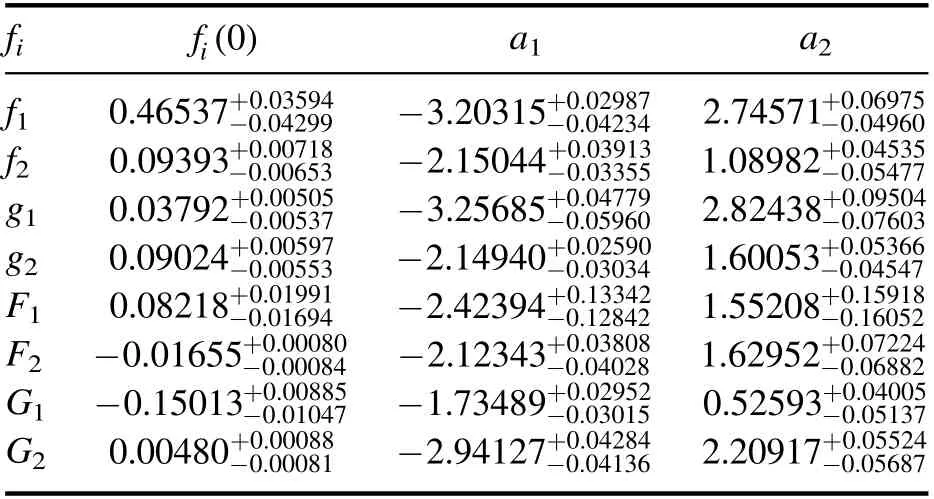
Table 2.Fitted parameters of form factors with the Ioffe-type current.
With form factors fitted by the dipole formula to the whole dynamical region, the decay widths of the processes Lb→Lγand Lb→Ll+l-can be calculated directly in aid of the formula (5) and (6).The decay width of the process Lb→Lγis determined by the form factors f2and g2at the zero momentum transferq2=0 GeV2.The form factors are estimated withs0= 39 ~41 GeV2and= 18~22 GeV2as
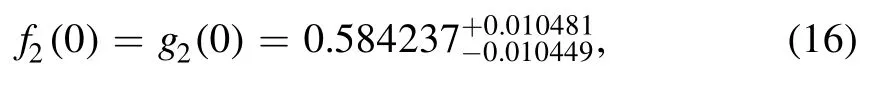
for the CZ-type current and
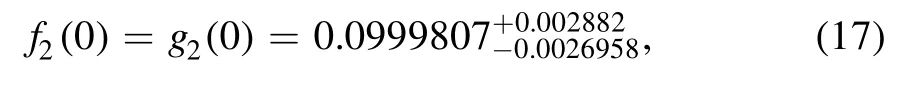
for the Ioffe-type current.

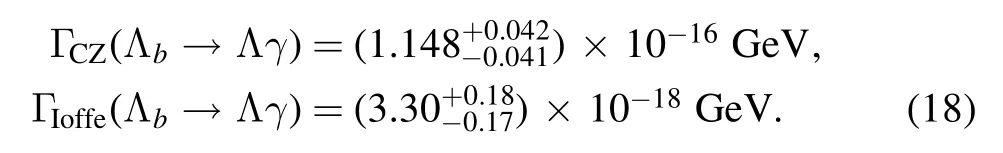
In calculations we use the lifetime of Lbasτ=1.471×10-12s[1].Therefore, the corresponding branch ratio of thedecay mode is obtained as

Table 3.Branch ratio of the process L b →Lγwith different models.
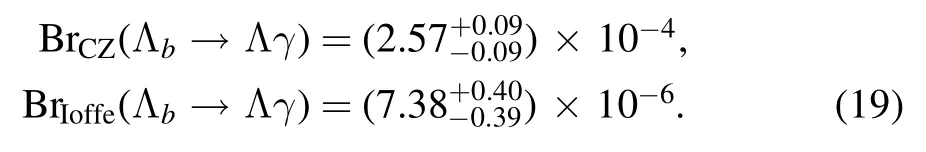
It is found that the interpolating current of the Lbbaryon can generate a fairly large difference when we estimate the branch ratio of the process.Compared with the experiments,it shows that the CZ-type current does not match well with the data,while results from the Ioffe-type are perfectly consistent with those from the PDG[1].The results are listed in table 3 with other methods and experimental data.
The decay width and branch ratio of the process Lb→Ll+l-can be calculated with a similar procedure.The Wilson coefficients are set as

In order to give the differential decay width, we need to extrapolate the form factors to the whole dynamic region.We use the fitted formula (15) to estimate the decay width with formula(6).It is noted that the differential decay width on the momentum transfer has a pole at the pointq2=0 GeV2, so results from the fit formula(15)are not applicable at the point.In the analysis, the whole dynamic region is chosen as 0.1 GeV2<q2<20.286 GeV2.The differential decay width is shown in figure 4.
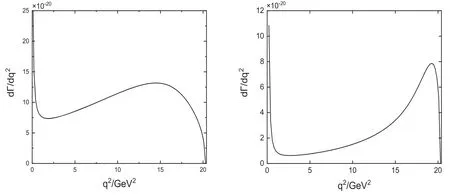
Figure 4.ProcessL b →Ll +l -decay rate relate with the transfer momentum q2 in (a) CZ-type current and (b) Ioffe-type current.
The total decay rate can be obtained by integrating the derivative one in the dynamic region 0.1 GeV2<q2<20.286 GeV2.In the analysis we ignore contributions from the region 0 ~0.1 GeV2because of the factorsandThe final result with CZ-type current is
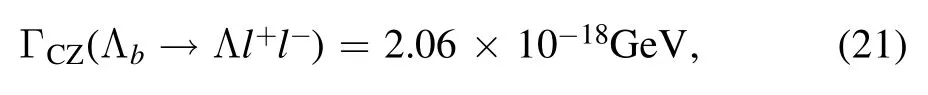
and that with Ioffe-type current is

In table 4, we list the corresponding branching ratios from various models and the experiment.It can be seen from the table that estimation from the Ioffe-type current matches better with the data from the PDG in comparison with other theoretical predictions.Another conclusion is that the choice of the interpolating current may affect the result to some extent and the Ioffe-type current is a more suitable choice for the processes of the description.
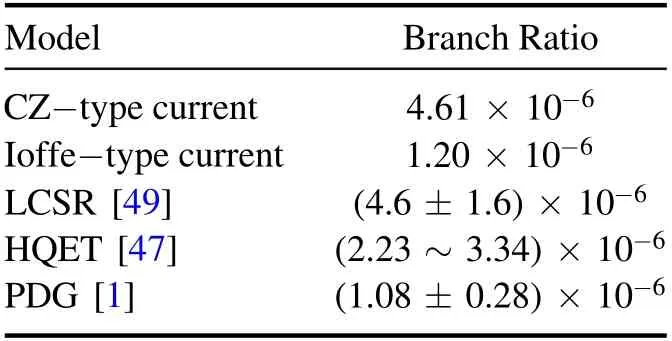
Table 4.Branch ratios of the decay processL b →Ll +l - from different models.
5.Summary and conclusion

The results show that the renewed distribution amplitudes may affect the results to some extent.In comparison with previous analysis, the predictions are much more compatible with the new data from the PDG.It can also be seen from the results that the Ioffe-type current is a more suitable choice in the description of the rare decay processes of the Lbbaryon.The CZ-type current is used to eliminate contributions that are not important on the light-cone, while results from the Ioffetype current may contain more complex structures and contain more detailed information,so Ioffe-type current may give relatively more reliable predictions.Therefore,our predictions for the branching ratios are Br( Lb→Lγ) =10-6and Br (Lb→Ll+l-) = 1.20 ×10-6.It is noted that the estimation of the process Lb→Lγis about one order lower than previous theoretical predictions from various models,and the result is well consistent with the renewed data from the PDG.
Appendix A.LCSR of the form factors
The LCSR of the form factors relating to the processes have been obtained in the previous work [21].Here we only present the results in this appendix for the completeness of the paper.
When we adopt CZ-type current for a Lbbaryon, we obtain the following form factors f1, f2, F1and F2:
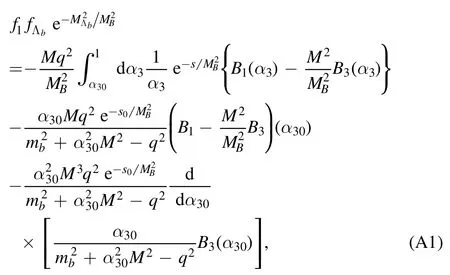

When we adopt Ioffe-type current for a Lbbaryon,we obtain the following form factors f1, f2, g1, g2, F1, F2, G1and G2:



Herein, the following definition is introduced:
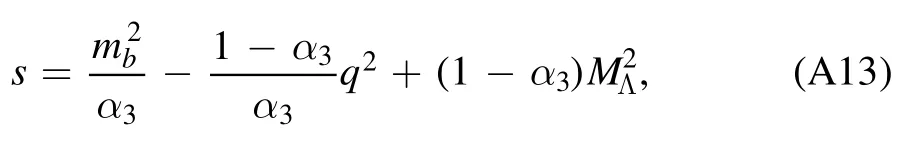
and the parameterα30is obtained at the points=s0
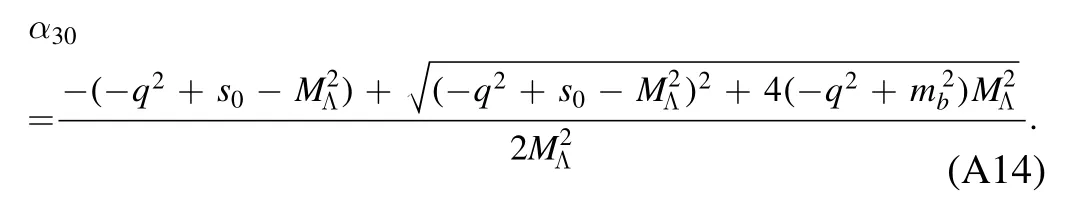
The distribution amplitudes with tildes are defined as:
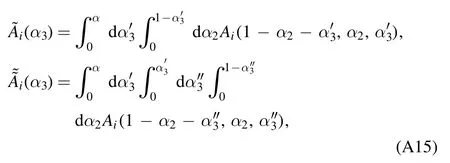
and we define the following abbreviations:
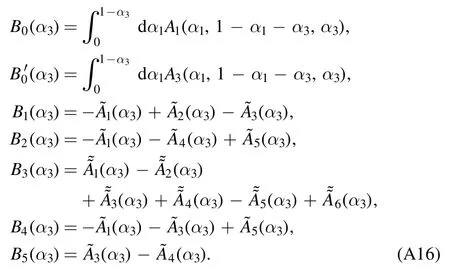
Appendix B.Light-cone distribution amplitudes of Λ with higher-order corrections
In this appendix,we present the distribution amplitudes of the Λ baryon considering corrections from the higher-order conformal spin expansion [24].The explicit expressions of the twist-3 distribution amplitudes are

The twist-4 distribution amplitudes are
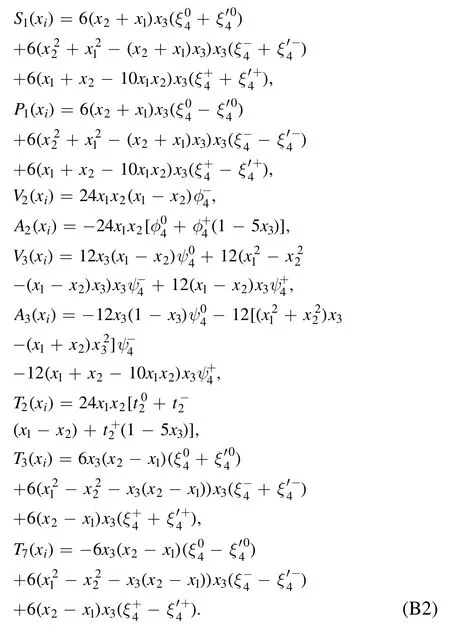
The twist-5 distribution amplitudes are

The twist-6 distribution amplitudes are
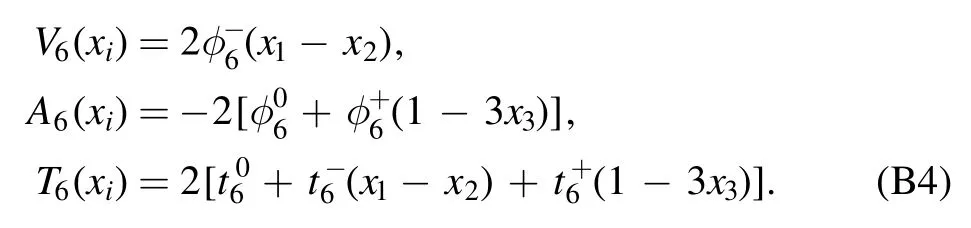
 Communications in Theoretical Physics2021年10期
Communications in Theoretical Physics2021年10期
- Communications in Theoretical Physics的其它文章
- Scalar one-loop four-point integral with one massless vertex in loop regularization
- Representations of hypergraph states with neural networks*
- A universal protocol for bidirectional controlled teleportation with network coding
- Strange quark star and the parameter space of the quasi-particle model
- Three-dimensional massive Kiselev AdS black hole and its thermodynamics
- Analysis of the wave functions for accelerating Kerr-Newman metric
