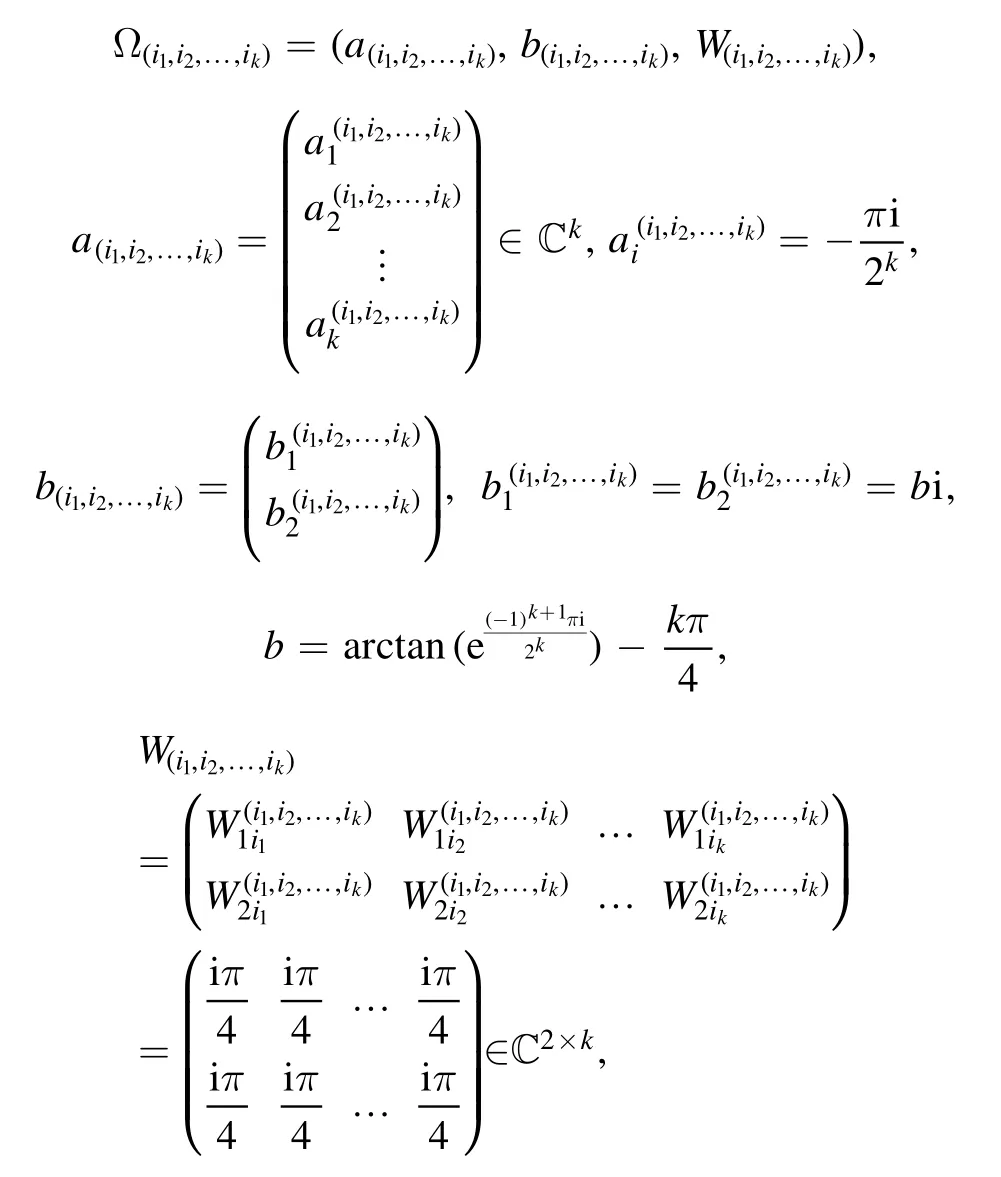
Representations of hypergraph states with neural networks*
Ying Yang (杨莹)and Huaixin Cao (曹怀信)
1 School of Mathematics and Information Technology, Yuncheng University, Yuncheng 044000, China
2 School of Mathematics and Statistics, Shaanxi Normal University, Xi’an 710119, China
Abstract The quantum many-body problem (QMBP) has become a hot topic in high-energy physics and condensed-matter physics.With an exponential increase in the dimensions of Hilbert space, it becomes very challenging to solve the QMBP,even with the most powerful computers.With the rapid development of machine learning, artificial neural networks provide a powerful tool that can represent or approximate quantum many-body states.In this paper, we aim to explicitly construct the neural network representations of hypergraph states.We construct the neural network representations for any k-uniform hypergraph state and any hypergraph state,respectively, without stochastic optimization of the network parameters.Our method constructively shows that all hypergraph states can be represented precisely by the appropriate neural networks introduced in [Science 355 (2017) 602] and formulated in [Sci.China-Phys.Mech.Astron.63 (2020) 210312].
Keywords: hypergraph state, neural network quantum state, representation
1.Introduction
In quantum physics, fully understanding and characterising a complex system with a large number of interacting particles is an extremely challenging problem.Solutions within the standard framework of quantum mechanics generally require knowledge of the full quantum many-body wave function.Thus, the problem becomes one of how to solve the manybody Schrödinger equation of a large dimension system.This is just the so-called quantum many-body problem(QMBP)in quantum physics, which has become a hot topic in highenergy physics and condensed-matter physics.When the dimension of the Hilbert space describing the system is exponentially large, it becomes very challenging to solve the QMBP, even with the most powerful computers.
Many methods have been used to overcome this exponential difficulty and solve the QMBP, including the tensor network method (TNM) [1–3] and quantum Monte Carlo simulation (QMCS) [4].However, the TNM has difficulty dealing with high-dimensional systems [5] or systems with massive entanglement [6]; the QMCS suffers from the sign problem [7].Thus, some new methods of finding the QMBP are required.
The approximation capabilities of artificial neural networks (ANNWs) have been investigated by many authors,including Cybenko [8], Funahashi [9], Hornik [10, 11],Kolmogorov [12], and Roux [13].It is known that ANNWs can be used in many fields, including the representation of complex correlations in multiple-variable functions or probability distributions [13], the study of artificial intelligence through the popularity of deep learning methods [14],and so on [15–19].
Undoubtedly, the interaction between machine learning and quantum physics will benefit both fields [20, 21].For instance, in light of the idea of machine learning, Carleo and Troyer [22] found an interesting connection between the variational approach in the QMBP and learning methods based on neural network representations.They used a restricted Boltzmann machine (RBM) to describe a many-body wave function and obtained an efficient variational representation by optimizing those variational parameters with powerful learning methods.Yang et al [23] researched an approximation of an unknown ground state of a given Hamiltonian using neural network quantum states.Numerical evidence suggests that an RBM optimized by the reinforcement learning method can provide a good solution to several QMBPs [24–31].
However,the solutions obtained are approximate but not exact.To find the exact solution of a QMBP using an ANNW,the authors of[32]introduced neural network quantum states(NNQSs) with general input observables from the mathematical point of view,and found some N-qubit states that can be represented by normalized NNQS, such as all separable pure states, Bell states, and Greenberger-Horne-Zeilinger (GHZ)states.Gao et al [33] showed that every graph state has an RBM representation(RBMR)and gave a simple construction of the RBMR for a graph state.
Lu et al[19]theoretically proved that every hypergraph state can be represented by an RBM with a {0, 1}input and obtained the RBMRs of 2-and 3-uniform hypergraph states,which are not the NNQS introduced by [22] and formulated in [32].What we care about is whether we can construct a neural network representation of any hypergraph state using the{1,- 1}-input NNQS considered in [22] and [32].
In this paper, we will aim to explicitly construct the neural network representations of arbitrary hypergraph states.In section 2, some notations and conclusions for NNQS with general input observables will be recalled and some related properties will be proved.In sections 3 and 4, the neural network representations for any k-uniform hypergraph state and any hypergraph state will be constructed, respectively,without stochastic optimization of the network parameters.
2.Neural network quantum states
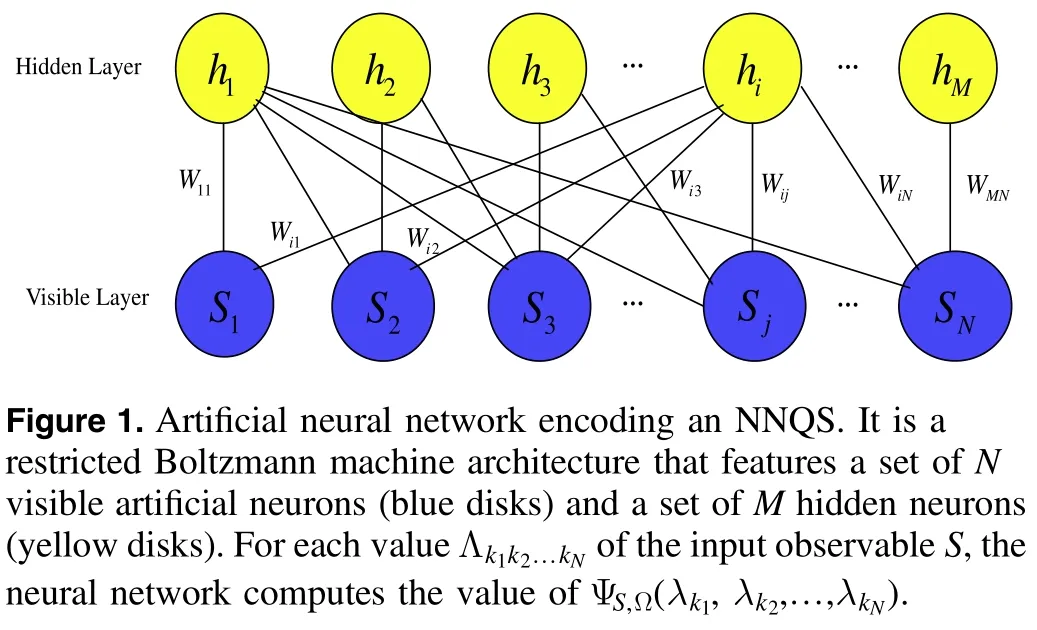
Let us start with a brief introduction to some notations in the neural network architecture introduced by [22] and formulated in [32].
LetQ1,Q2, … ,Q Nbe N quantum systems with state spaces H1, H2, … ,HNwith dimensions ofd1,d2, … ,d N, respectively.We consider the composite system Q ofQ1,Q2, …,QNwith the state space H ≔H1⊗ H2⊗…⊗HN.

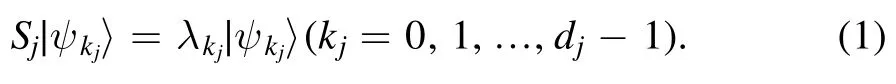
It is easy to check that the eigenvalues and corresponding eigenbasis ofS=S1⊗S2⊗ … ⊗SNareλ k1λk2…λkN,
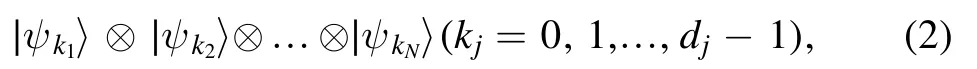
respectively.We write
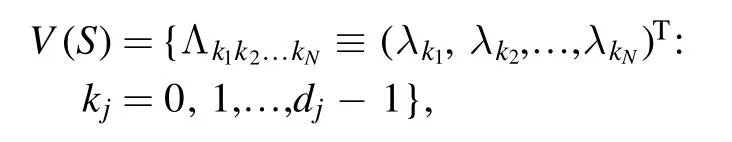
which is called an input space.For parameters
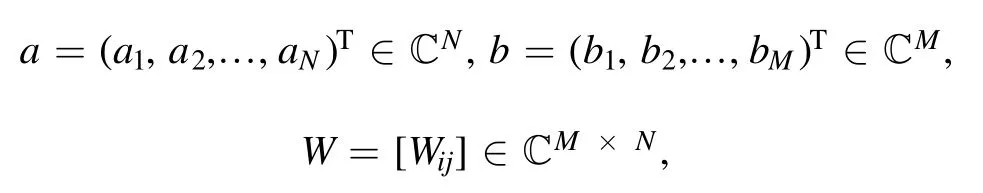
we write Ω =(a,b,W) and
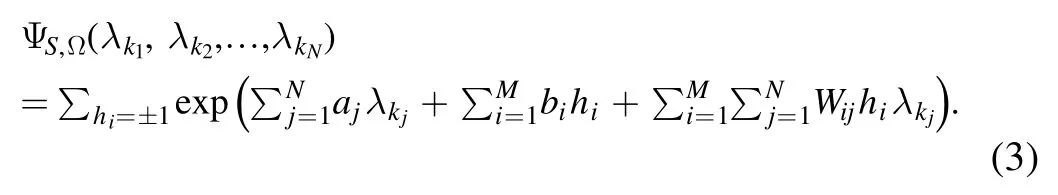
We then obtain a complex-valued function ΨS,Ω(λ k1,λk2,… ,λkN)of the input variable Lk k…kN12.We call it a neural network quantum wave function (NNQWF).It may be identical to zero.In what follows,we assume that this is not the case,that is, we assume thatfor some input variable Lk1k2…kN.We then define
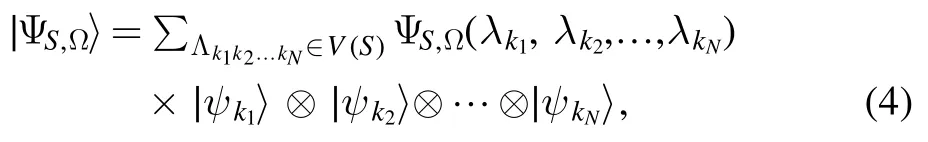
which is a nonzero vector(not necessarily normalized)of the Hilbert spaceH.We call it a neural network quantum state(NNQS) induced by the parameter Ω =(a,b,W) and the input observableS=S1⊗S2⊗ … ⊗SN(figure 1).
The NNQWF can be reduced to
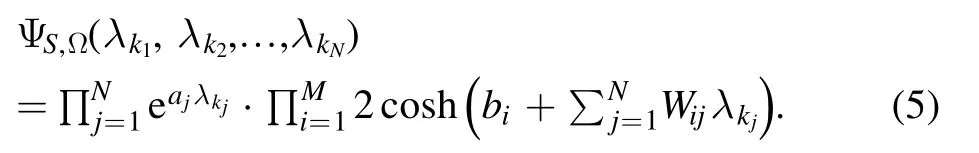
There is a special class of NNQSs; when1 ≤j≤N,we have
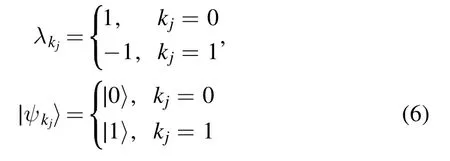
andV(S) = {1 , -1}N.
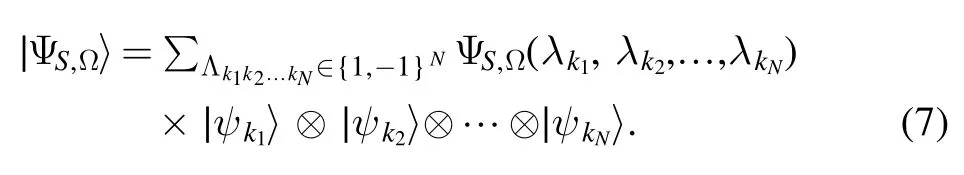
In this case, the NNQS (4) becomes This leads to the NNQS introduced in [22] and discussed in[34].We call such an NNQS a spin-z NNQS.
From the definition of an NNQWF, we can easily obtain the following results.
Proposition 1.If a hidden-layer neuronhM+1is added into an RBM with NNQWF ΨS,Ω(λ k1,λk2,… ,λkN), then the NNQWF ΨS,Ω′(λ k1,λk2,… ,λkN) of the resulting network reads
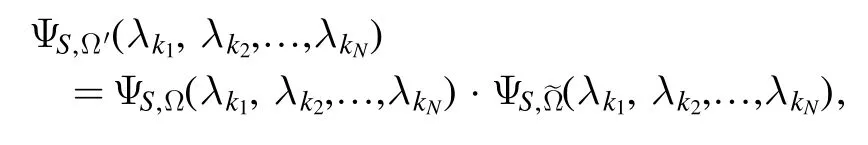
where
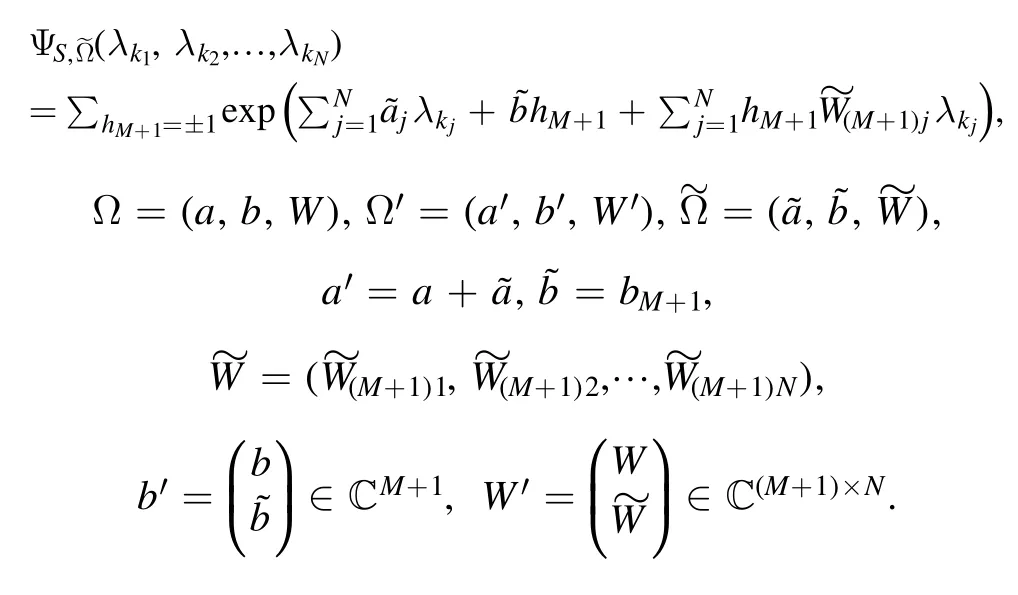
This result can be illustrated by figure 2.
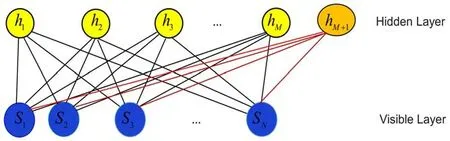
Figure 2.The network that results from adding a hidden-layer neuronhM +1 into a network with visible layersS1 , S2, …, SN and hidden layersh1 , h2, …, h M.
Proposition 2.Supposing that ΨS,Ω′(λ k1,λk2,… ,λkN) and ΨS,Ω″(λ k1,λk2,… ,λkN)are two spin-z NNQWFs with the same input observable
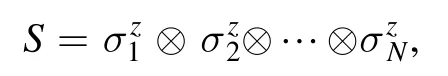
and the individual parameters
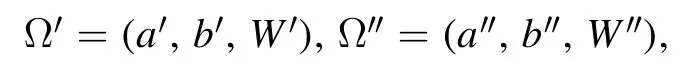
respectively.Then
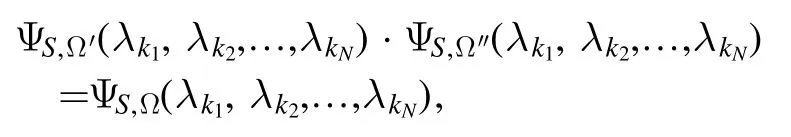
where
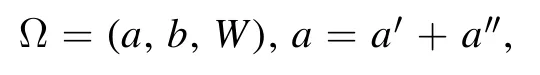
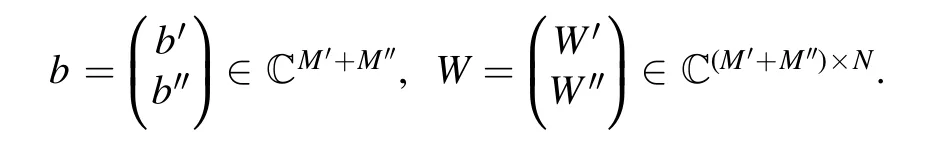
3.Neural network representations of k-uniform hypergraph states
Generally,for a given pure state∣ψ〉 ,if an NNQS ∣ΨS,〉Ωand a normalized constant z exist, such that∣ψ〉 =z∣ΨS,Ω〉, then we say that∣ψ〉 can be represented by the NNQS ∣ΨS,〉Ω.The authors of [32] found some N-qubit states that can be represented by a normalized NNQS, such as all separable pure states, Bell states, and GHZ states.It was proved in [33] and[19] that all graph states and all hypergraph states can be represented by an RBM with a {0, 1}input.
In this section, we aim to construct a neural network representation of any k-uniform hypergraph state by using {1, −1}-input NNQS given by [22], rather than {0, 1}-input NNQS.
To do this,let us start by briefly recalling the definition of the k-uniform hypergraph state, which is an extension of the concept of graph state.A k-uniform hypergraph[35]is a pairGk=(V,E) consisting of a setV= {1 , 2,… ,N} and a nonempty set E of some k-element subsets of V.The elements of V and E are called the vertices and k-hyperedges of Gk,respectively.Whene= (i1,i2,… ,i k) ∈E, we say that the verticesi1,i2, … ,i kare connected by e.
Thus, a graph in the common sense is just a 2-uniform hypergraph.
Given a k-uniform hypergraphGk=(V,E), the k-uniform hypergraph state∣Gk〉was defined in [35], as follows:
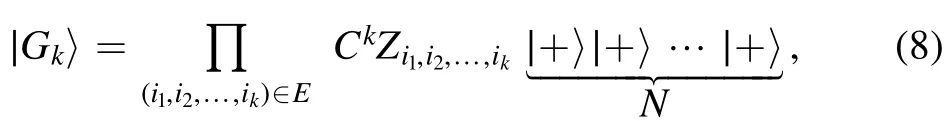
where
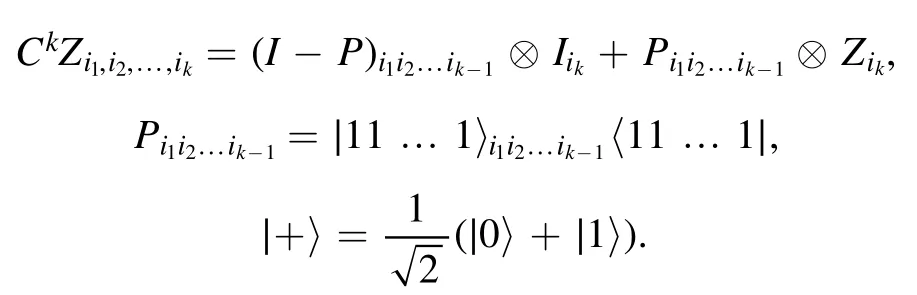
In fact,
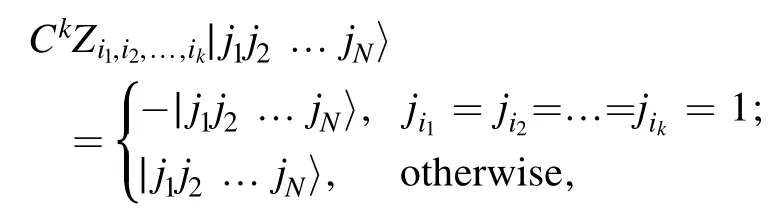
for allj1,j2,… ,jN=0, 1.Thus,
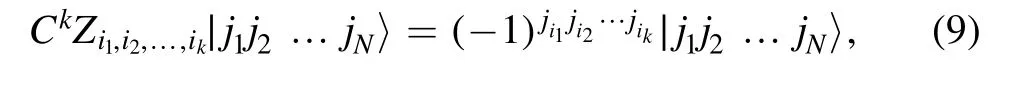
for allj1,j2,… ,jN=0, 1.
Here, we try to construct neural network representations for any k-uniform hypergraph state∣Gk〉, that is to fnid an NNQS∣ΨS,Ω〉such that ∣Gk〉 =z∣ΨS,Ω〉for some normalized constant z.
First, we reduce equation (8) for a k-uniform hypergraph state by the next procedure.
Since
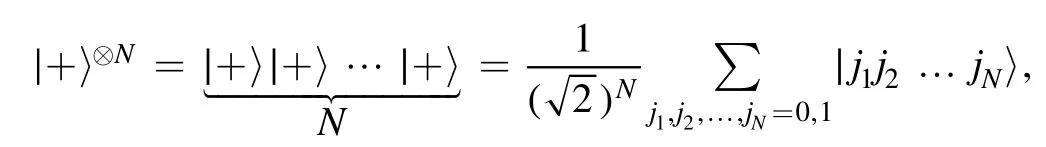
we see from (9) that
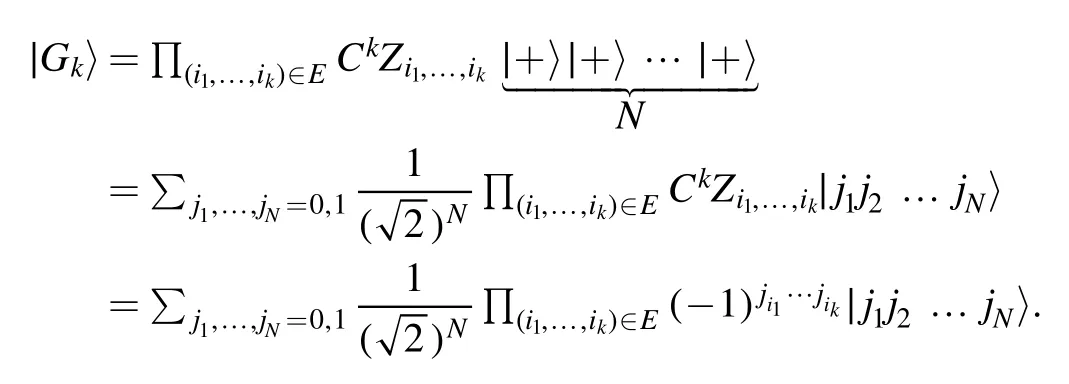
Given that
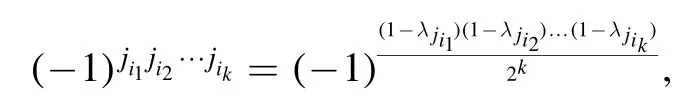
we obtain
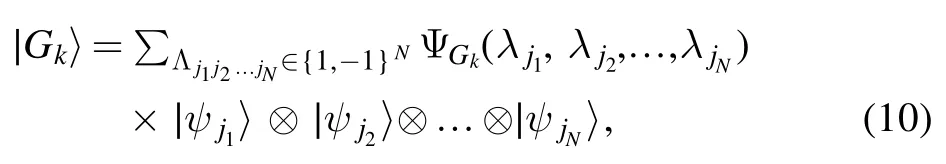
where
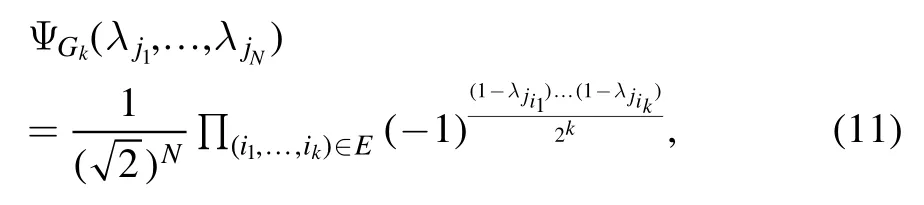
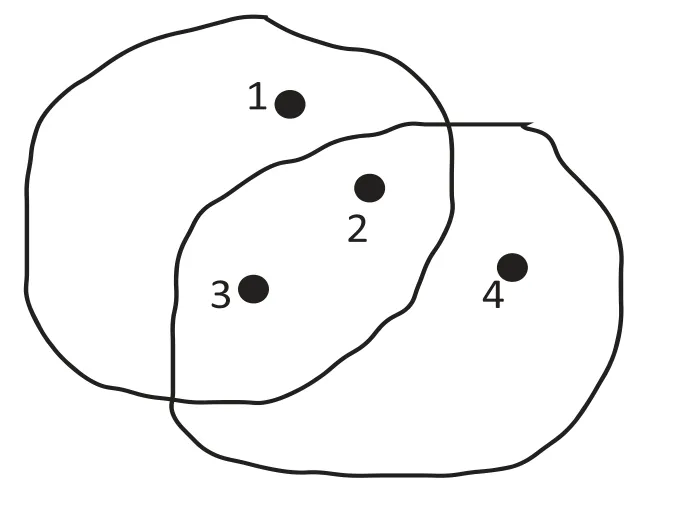
Figure 3.A 3-uniform hypergraph with four vertices.
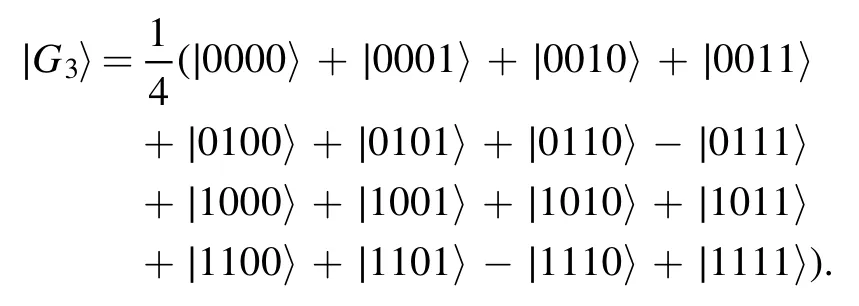
In addition, using this simplification equation (10), the k-uniform hypergraph state obtained is similar to a spin-z NNQS equation (7), which sets the stage for our followup work.
Besides, the wave function of the k-uniform hypergraph state∣Gk〉is given by (11).By writing
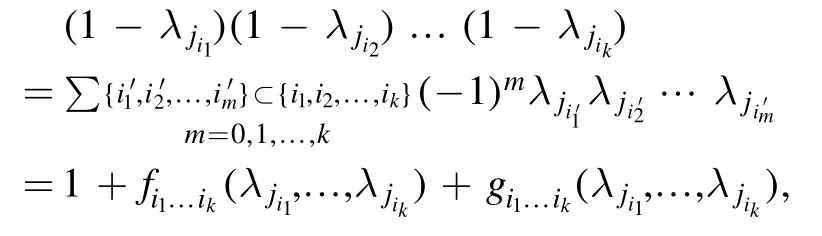
where
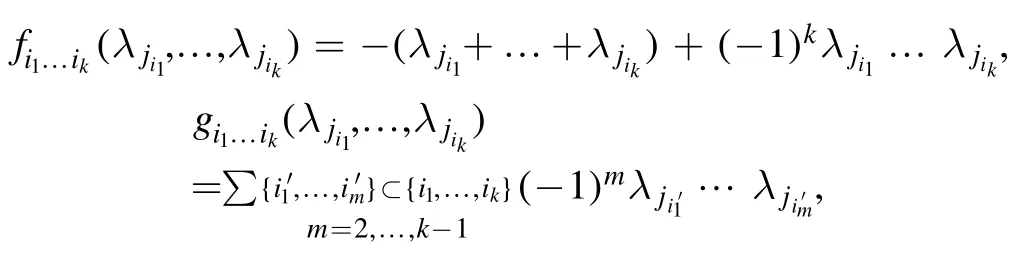
we get
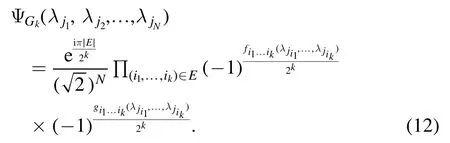
Next, we try to construct an NNQWFΨS,Ω(λj1,λj2, … ,λjN), such that
for some constant z, where
Case 1.k = 1.LetE= {(m1) , (m2), … ,(ms)},∣E∣=s.From the discussion above, we can easily find that the wave function of the 1-uniform hypergraph state∣G〉1is
Let Ω1=(a,b,W), where
The NNQWF with these parameters then reads
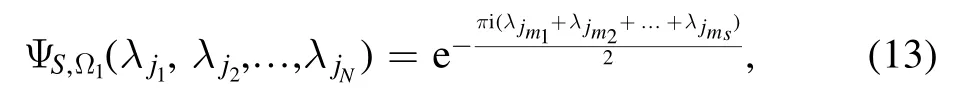
and so
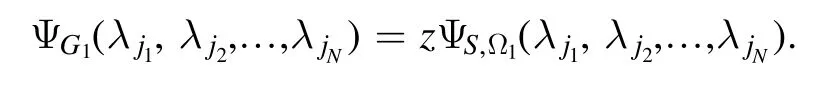
This implies that any 1-uniform hypergraph state∣G〉1can be represented by a spin-z NNQS.
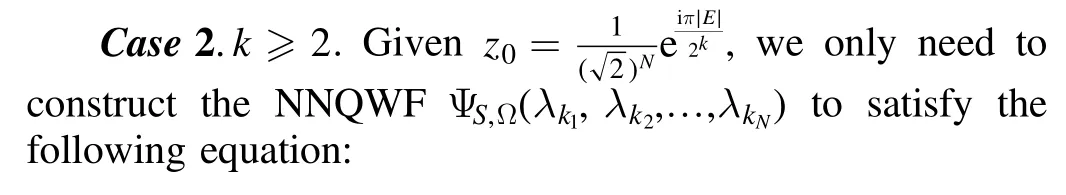
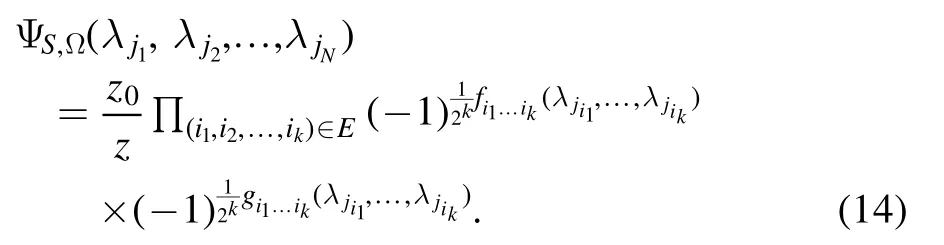
To construct the NNQWF ΨS,Ω(λ k1,λk2,… ,λkN) ,we first represent the function
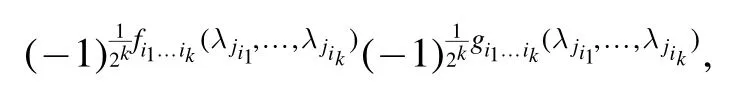
as some small NNQWFs for each (i1,i2,… ,i k) ∈E, and then proceed to construct the NNQWF that we needed.
Step 1.Noting that
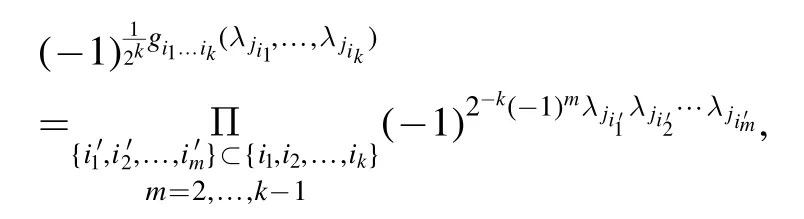
we first write each factor
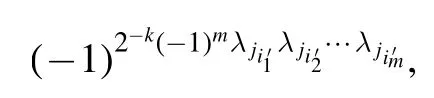
as an NNQWF.To do this, form= 2, 3,… ,k-1 andwe write

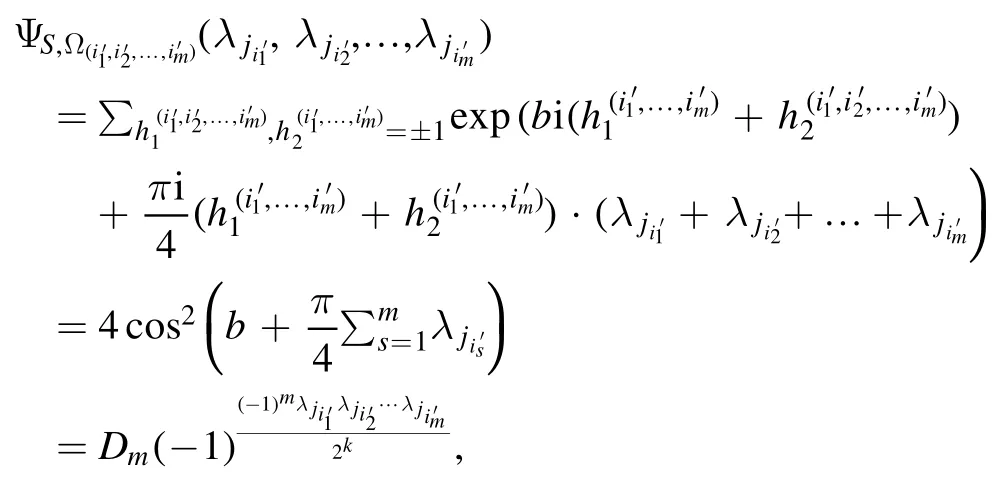
where

This shows that
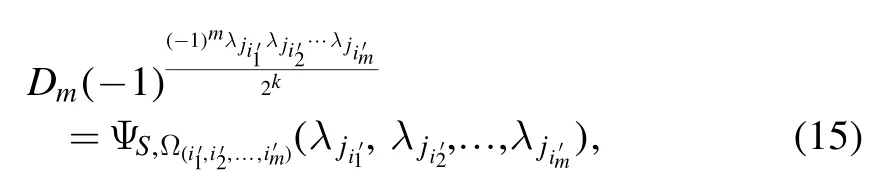
for anym= 2, 3,… ,k-1.This implies that the function
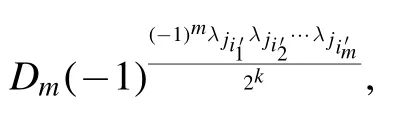
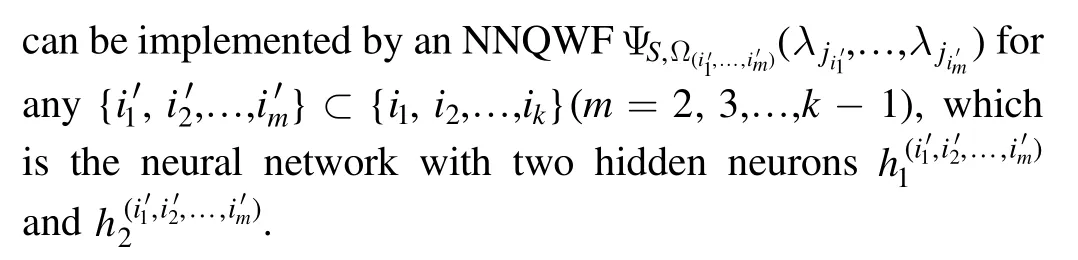
Step 2.To represent
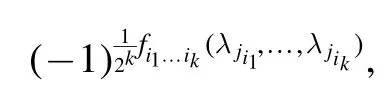
as an NNQWF for each (i1,i2,… ,i k) ∈E, we write
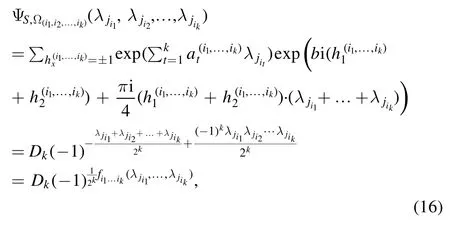
where

This implies that
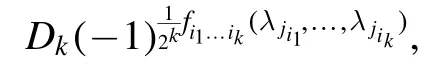
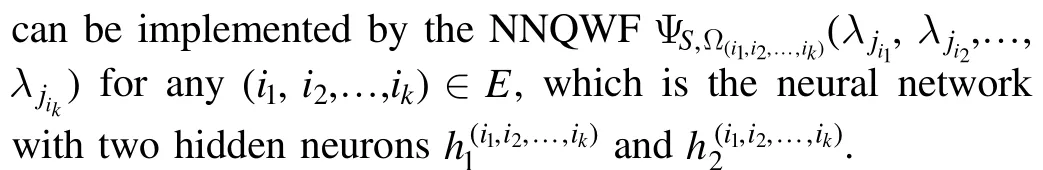
Step 3.Furthermore, using equations (15) and (16), the right-hand side of equation (14) becomes
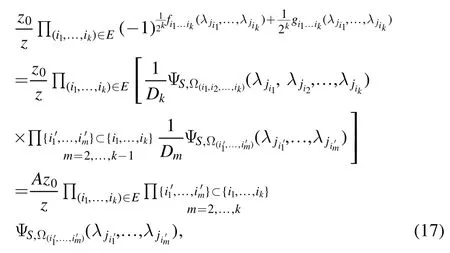
To label the elements of E, we write
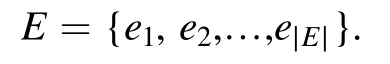
Whenet= (i1,i2,… ,ik), we let
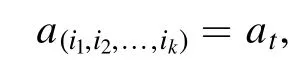
and label the set
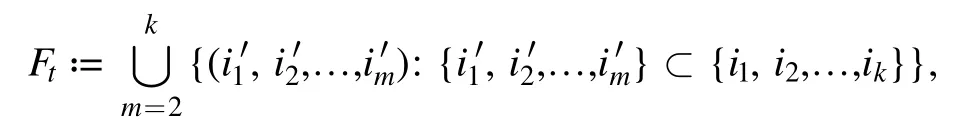
as
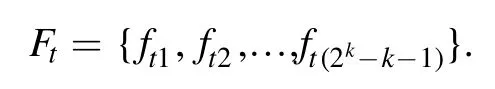
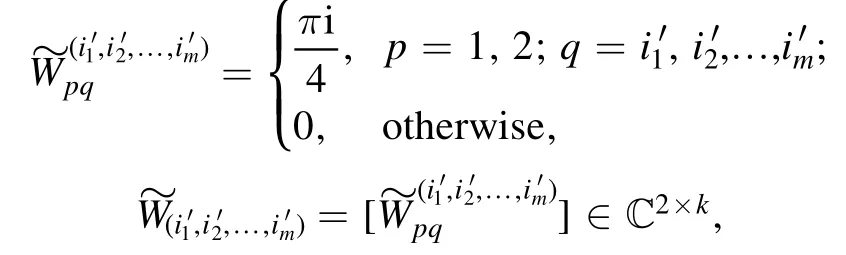
wherep= 1, 2;q= 1, 2,… ,kand define
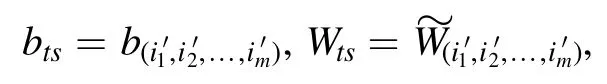
and let
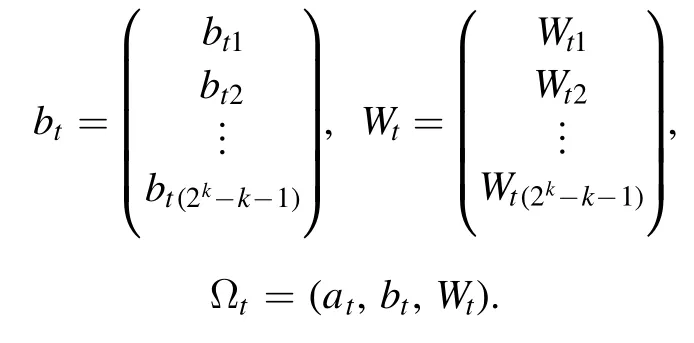
Using proposition 2, we have
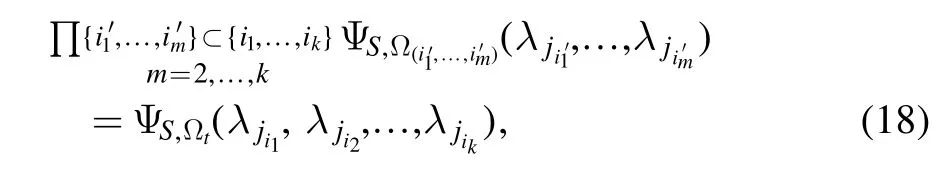
for everyet= (i1,i2,… ,ik).
Step 4.Furthermore, we let
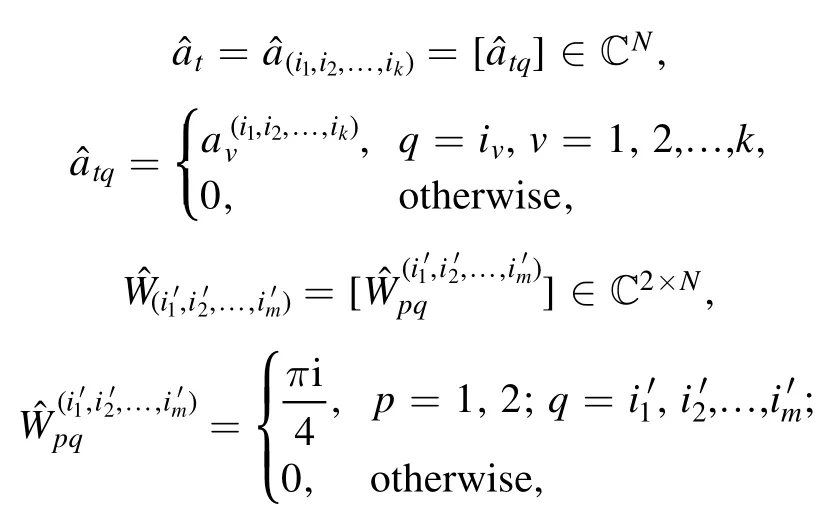
forp= 1, 2;q= 1, 2,… ,N, and
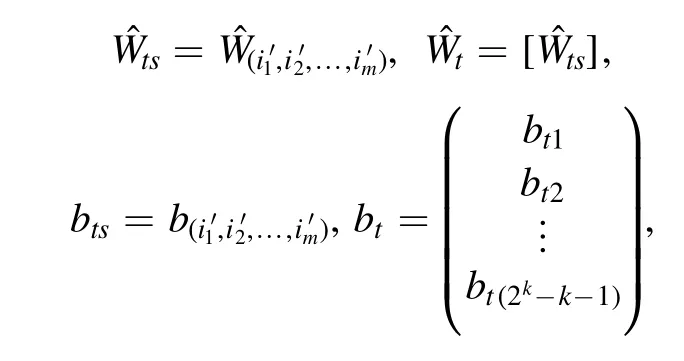
fort= 1, 2,… , ∣E∣ ,s= 1, 2,… ,2k-k-1.We write
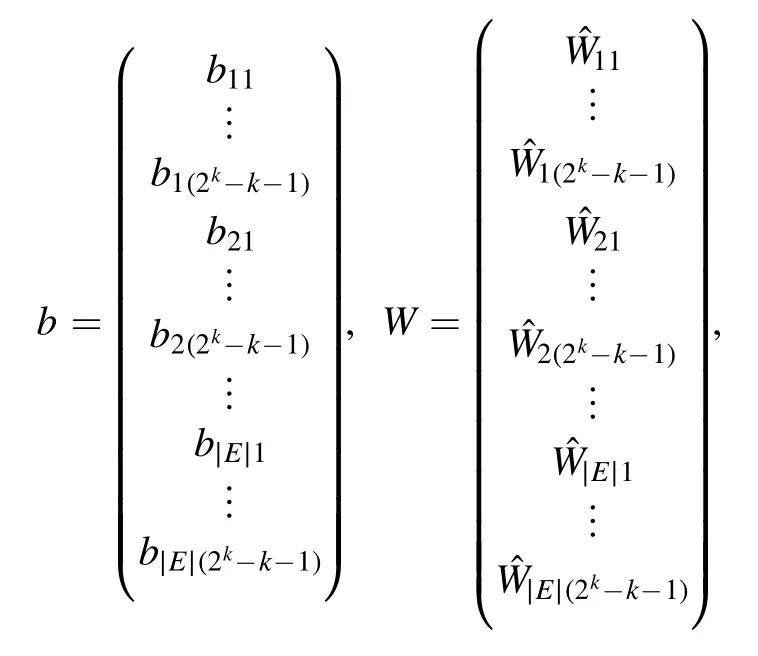
and
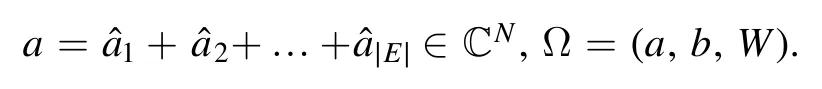
Using proposition 2, we obtain:
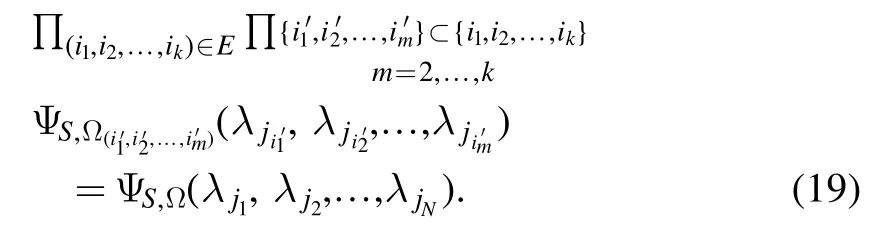
Let
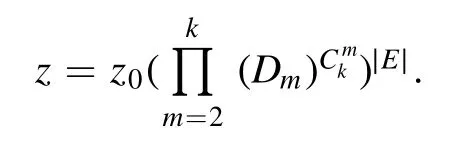
Using equations (17) and (19) then yields that
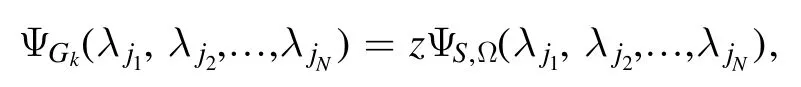
We have constructed now an NNQWF ΨS,Ω(λj1,λj2,… ,λjN) that satisfies equation (14).This leads to the following conclusion.
Theorem 1.Any k-uniform hypergraph state∣Gk〉can be represented by a spin-z NNQS (7) given a neural network with a{1,- 1}input.
Example 1.Consider a hypergraph G with three vertices and a 3-hyperedgee1=(1 , 2, 3)which is represented by the lefthand side of figure 4.In this case, the wave function of the 3-uniform hypergraph state ∣G〉 reads
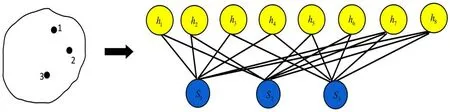
Figure 4.Neural network representation of the hypergraph state which corresponds to a hypergraph consisting of three vertices 1, 2, 3, Si =i =1, 2, 3.
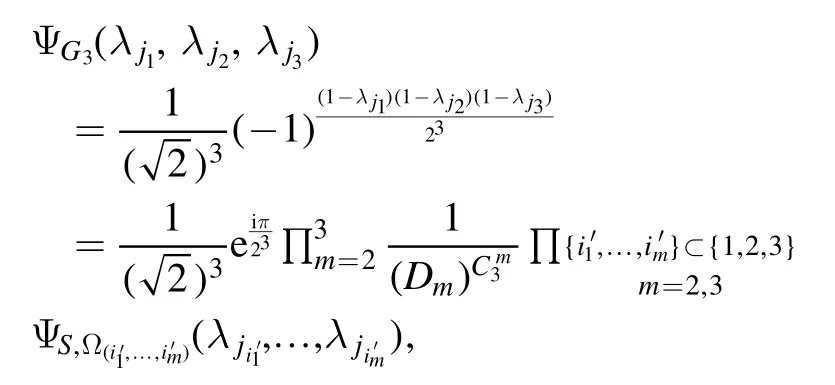
which is a constant multiple of the NNQWF
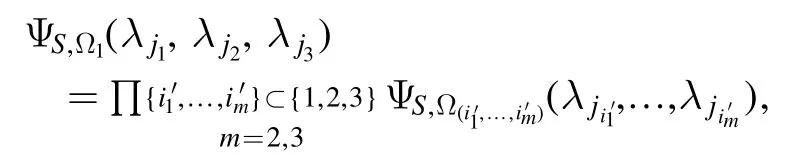
with the parameter Ω1=(a1,b1,W1) where
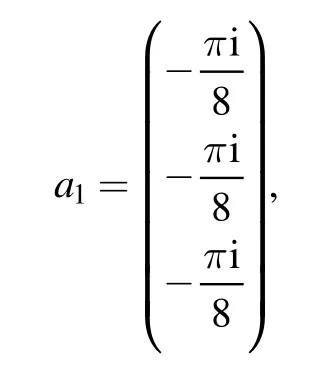

That is,
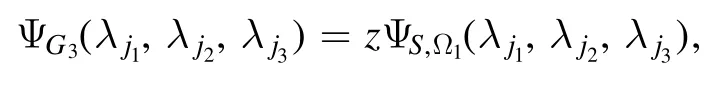
where
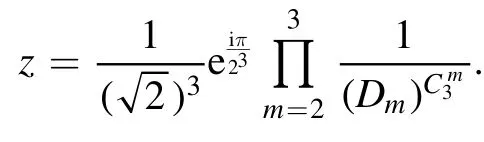
The neural network that generatesis given on the right-hand side of figure 4.
Example 2.Neural network representation of k-uniform hypergraph state corresponding to a given k-uniform hypergraph.The representation process is shown in figure 5 below.In this case, the parameters are
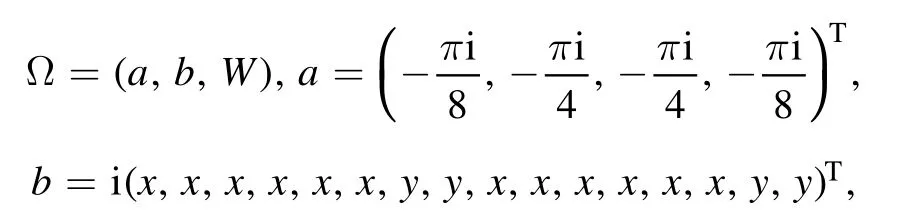
wherex=y= arctan,
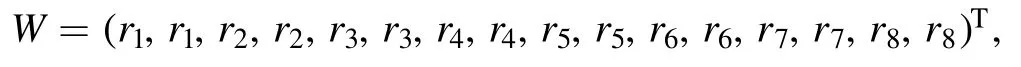
with
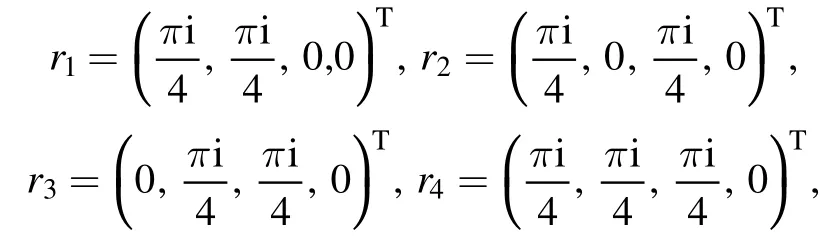

Figure 5.Neural network representation of k-uniform hypergraph states.The first figure is a hypergraph representation of a 3-uniform hypergraph state.The second one i s an idea of the process;it shows a neural network representation of the 3-uniform hypergraph state,where E ={(1 , 2, 3) , (2 , 3, 4)}, Si =i = 1,… ,8.
Remark 1.We see from Example 1 and Example 2 that the number of visible-layer neurons is equal to the number of vertices of the k-uniform hypergraph, and the number of hidden-layer neurons is ∣E∣ (2k+1- 2k-2).This is a general rule for the neural network representation of any k-uniform hypergraph state.
4.Neural network representations of hypergraph states
A hypergraph is a generalization of the concept of a k-uniform hypergraph state, defined as follows.
A hypergraph [35] is a pairG=(V,E) consisting of a setV= {1 , 2,… ,N} and a nonempty set E of subsets of V.The elements of V and E are called the vertices and hyperedges of G,respectively.Whene= (i1,i2,… ,i k) ∈E,we say that the verticesi1,i2, … ,i kare connected by e.Hence, E is a set of any k-hyperedges, where k is no longer fixed but may range from 1 to N.
Given a mathematical hypergraphG=(V,E) [35], one can construct the corresponding hypergraph state as follows[35]:
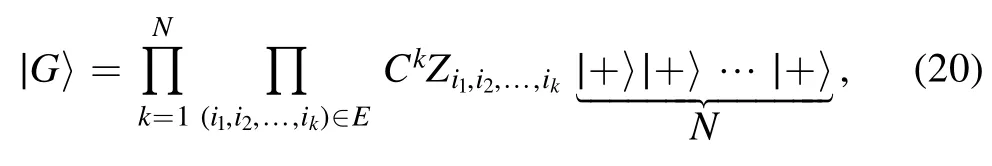
where
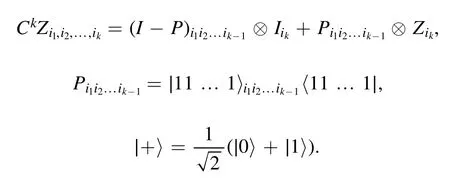
Here, we try to construct neural network representations for any hypergraph state ∣G〉 , that is, we try to find an NNQS∣ΨS,Ω〉such that ∣G〉 =z∣ΨS,Ω〉for some normalized constant z.
At first,we reduce equation(20)for the hypergraph state using equation (11) and obtain that
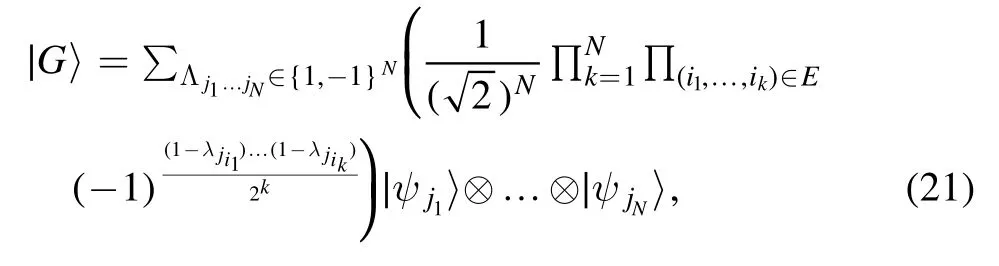
whereλji1,… ,λji1, ∣ψj1〉 ,… , ∣ψjN〉,are shown in equation (6).We see that the simplified equation(21)is simpler and easier to use.Given a hypergraph, we can use this expression to obtain a hypergraph state associated with it very quickly.For example, for the hypergraph in figure 6, the corresponding hypergraph state is
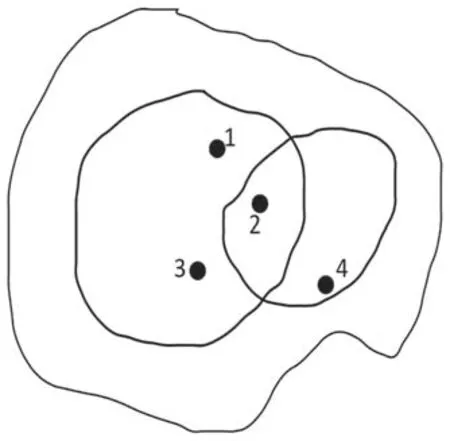
Figure 6.A hypergraph.
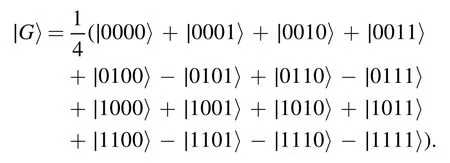
In addition,through this simplification equation(21),the hypergraph state obtained is similar to the spin-z NNQS equation, (7), which sets the stage for our follow-up work.
Besides, we can obtain that the wave function of hypergraph state ∣G〉 is
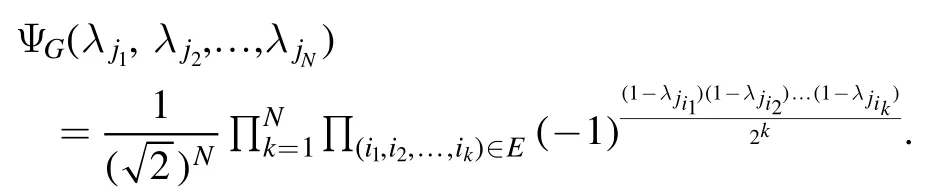
Next, we try to construct an NNQWFλjN), such that
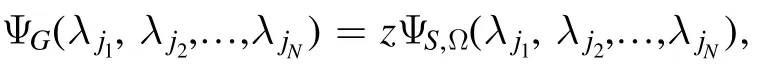
for some constant z.
When k = 1, we let
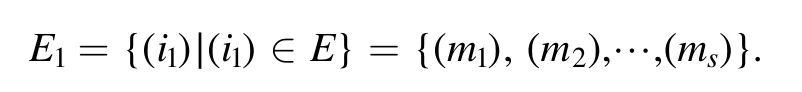
We can then see from section 3 that
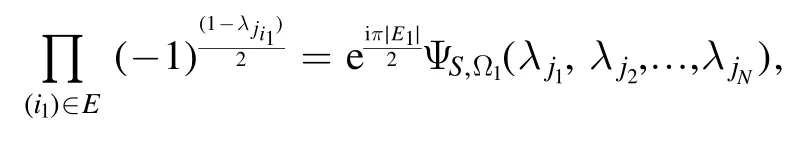
When k = 2,…,N, we let
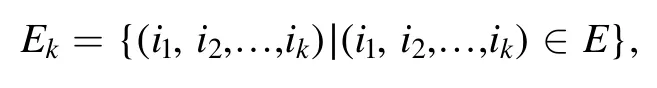
i.e.Ekis the set of superedges of k vertices.Using equations (12), (14), (17) and (19), we then find that a parameter Ωk=(ak,bk,Wk) exists, such that
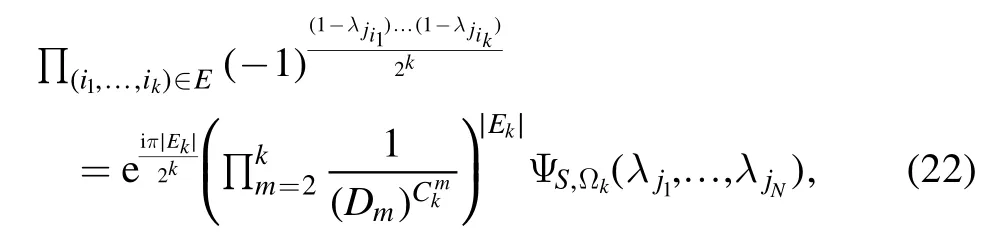
where∣Ek∣is the cardinality of the set Ek.
Furthermore, we have
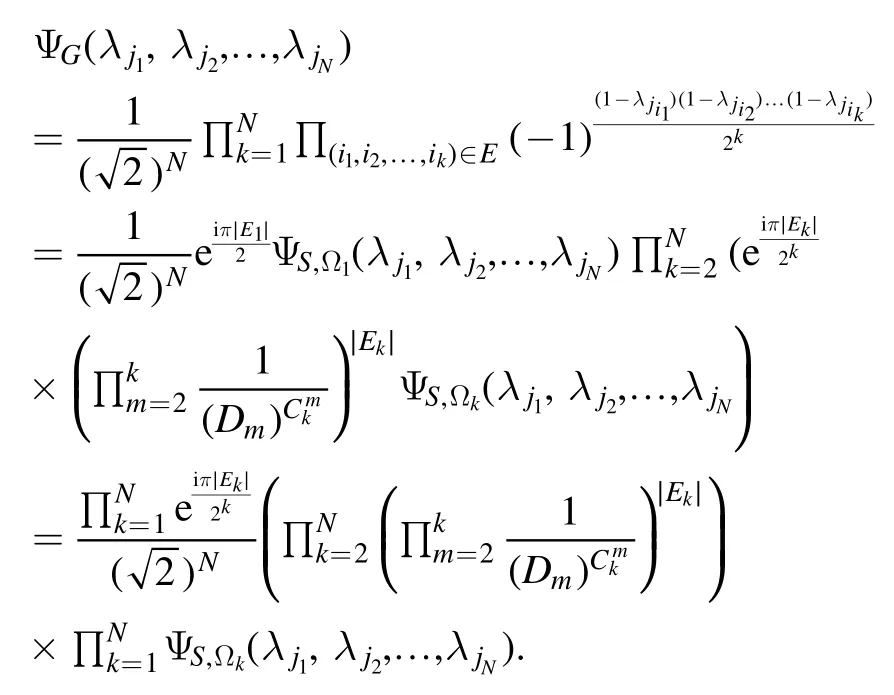
Using proposition 2,we can obtain that there exists a set of parameters Ω, such that
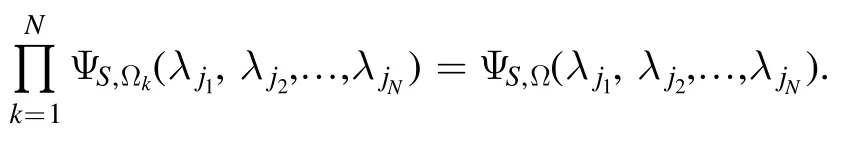
Put
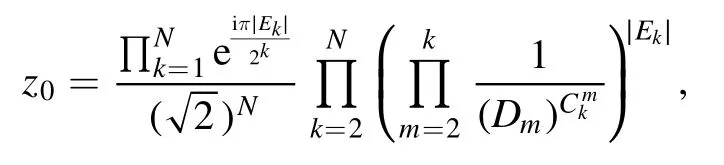
thus
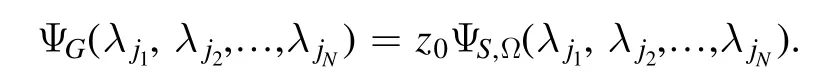
This leads to the following conclusion.
Theorem 2.Any hypergraph state can be represented as a spin-z NNQS (7) given a neural network with a{1,- 1}input.
5.Conclusions
In this paper, we have constructed a neural network representation for any hypergraph state.Our method constructively shows that all hypergraph states can be precisely represented by appropriate neural networks as proposed in [Science 355(2017) 602] and formulated in [Sci.China-Phys.Mech.Astron.63(2020) 210312].The results obtained will provide a theoretical foundation for seeking approximate representations of hypergraph states and solving the quantum manybody problem using machine-learning methods.
ORCID iDs
 Communications in Theoretical Physics2021年10期
Communications in Theoretical Physics2021年10期
- Communications in Theoretical Physics的其它文章
- Scalar one-loop four-point integral with one massless vertex in loop regularization
- A universal protocol for bidirectional controlled teleportation with network coding
- Improved analysis of the rare decay processes of Λb
- Strange quark star and the parameter space of the quasi-particle model
- Three-dimensional massive Kiselev AdS black hole and its thermodynamics
- Analysis of the wave functions for accelerating Kerr-Newman metric
