文家坡煤矿回采巷道底板破坏深度研究

王树明，王磊

(陕西彬长文家坡矿业有限公司，陕西 咸阳市 713500)

0 引言

随着开采规模和开采深度的不断加大，矿山回采巷道底板在复杂的工程地质条件和煤帮支承压力的综合影响下极易发生变形破坏，对底板的有效控制成为亟待解决的技术难题，因此，众多专家和技术人员对底板变形破坏机理进行了长期系统的研究。康红普等[1-3]认为底板岩层的挠曲、偏应力作用及岩石遇水软化是巷道底鼓的主要成因；文志杰等[4]通过建立底鼓力学分析模型得出了影响巷道底鼓量的主要因素是底板超挖深度和反底拱伸出段长度；谷拴成等[5]基于黏弹性流变模型推导出巷道底板底鼓量随时间变化的规律；SUN Jin[6]通过数值模拟软件研究得出切槽卸压能有效控制巷道底鼓的结论；TSANG P等[7]建立了底板岩梁力学模型，认为底板的破坏可分为剪切破坏和拉伸破坏 2种模式；贺永年等[8]通过现场监测发现巷道底鼓是由顶板压力通过两帮传递到底板后导致两帮和底板协同下沉，并且提出利用实测参数估算底鼓的各变形分量；王卫军等[9]认为工作面超前支承压力是巷道底鼓的主要影响因素，加固帮、角可有效提高回采巷道围岩的整体稳定性；于远祥等[10]运用极限平衡方法讨论了巷道两帮煤体荷载传递机理及其极限平衡区。上述研究成果对底鼓灾害的有效控制发挥了积极的指导作用，但由于煤矿巷道应力状况和围岩性质的复杂性，至今尚没有统一的认识，从而导致底鼓控制措施的盲目性和对经验的依赖性，使得底鼓治理效果并不理想。实际上，对底板而言，两帮煤体起着传递应力的作用，底鼓的发生及发展与两帮支承压力的分布密切相关。

因此，本文基于弹性基础梁模型来分析支承压力作用下文家坡煤矿 4102运顺煤帮的变形规律，在确定极限平衡区宽度的基础上讨论其底板的最大破坏深度，进而为该巷道煤帮及底板的支护设计提供科学的理论依据。

1 工程力学模型

1.1 巷道煤帮及底板变形破坏现状

文家坡煤矿地处陕西省彬州市境内，该矿4102运顺巷道是一设计断面尺寸为宽5 m×高3 m的矩形巷道，巷道沿4煤层底板掘进，煤层厚度为2.9～3.3 m，埋深为534.3～741.3 m，直接顶为中粒砂岩，厚度为22.26 m；老顶为泥质粉砂岩，厚度为24.9 m；直接底为细粒砂岩，厚度为5.98 m，遇水易泥化。老底为泥质粉砂岩，厚度为8.17 m。

4102运顺现场调查结果表明，该巷道里程1255～1278 m区间段，开挖后不久即发生不同程度的变形破坏，主要表现为较为严重的两帮鼓出和底板隆起，导致支护困难。

1.2 巷道围岩物理力学参数试验分析

为研究4102运顺4煤层围岩力学特性，通过在巷道内进行现场采样并在室内加工制作标准试件进行试验测试，所得煤样基本物理力学参数见表1。

表1 4102运顺煤体物理力学参数

工程实践表明，巷道围岩变形的基本因素包括自然因素和人为因素两方面。由现场调查和室内试验结果可知，文家坡煤矿4102运顺4煤呈半暗型煤，丝绸-油脂光泽，阶梯-参差状断口，局部可见裂隙，内充填黄铁矿薄膜；直接底呈灰白色，中厚层状，局部斜层理，层面可见个别煤屑，中部夹有粉砂岩薄层。该巷道煤帮及底板的变形破坏与煤帮及底板岩体的岩性密切相关。

1.3 巷道煤帮力学模型

现场调查表明，文家坡煤矿巷道的底鼓类型属于挤压流动性底鼓。4102运顺开挖后，围岩压力重新分布，两帮一定范围煤体所受垂直应力增高，形成支承压力。当煤体较为松软时，煤帮边缘将首先向巷道内鼓出。文家坡煤矿巷道的挤压流动性底鼓模型如图1所示。

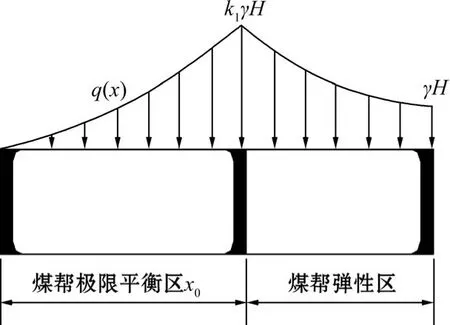
图1 煤帮支承压力分布模型

以巷道单位纵向深度的煤帮岩体作为分析对象，由于煤帮极限平衡区宽度远小于巷道纵向长度，因此，建立煤帮平面应变分析模型如图2所示。

图2 煤帮弹性地基梁计算模型

2 支承压力作用下煤帮变形分析

2.1 极限平衡区支承压力下煤帮变形分析

当仅考虑煤帮极限平衡区上方支承压力下煤体任一截面i的变形时，其计算模型如图3所示。

图3 极限平衡区岩体内力分析

由三角关系可知截面i处的支承压力为：

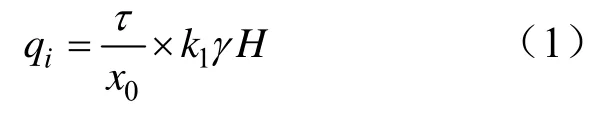
式中，k1、γ及H分别为应力集中系数、上覆岩层平均容重和埋深。

设截面i处为原点，且向右为正，则在区间τ上支承压力的分布为：

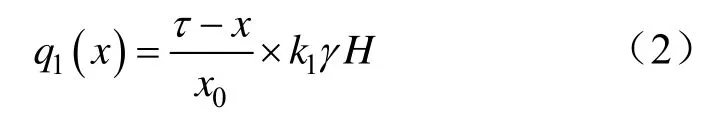
式中，τ≤x≤0。

同理可得支承压力在区间s上的分布规律为：

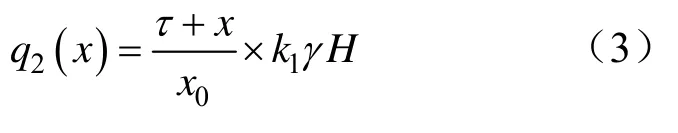
式中，0≤x≤s。

在煤帮极限平衡区取 dx段煤体进行研究，其受力模型如图4所示。

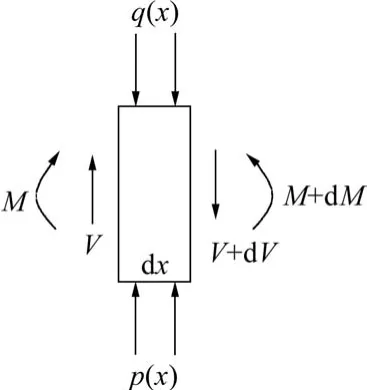
图4 煤帮微单元体分析模型[10]

将q(x)dx作为集中荷载，则由弹性地基梁在集中荷载作用下的解可得 4102运顺煤帮极限平衡区内任一单元岩体的内力解。

由集中荷载下弹性地基梁模型的剪力解析解可得任一单元岩体剪力v1为：

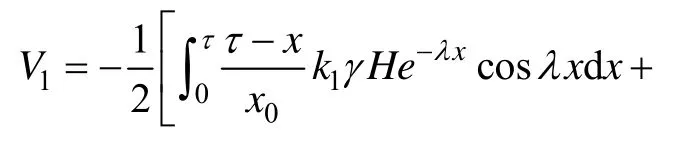
式中，λ为回采巷道两帮下卧底板的弹性特征值，

2.2 弹性区支承压力下煤帮变形分析

支承压力下弹性区岩体的内力分析模型如图 5所示。

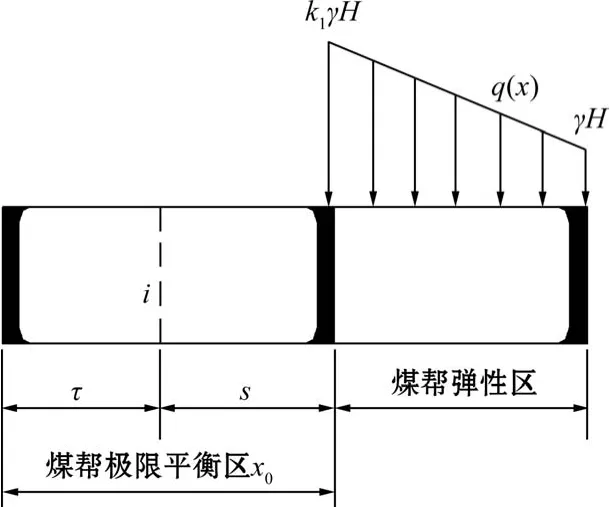
图5 弹性区岩体内力分析

为便于讨论，可将支承压力简化为三角形荷载和均布荷载两种工况。均布荷载下任一单元岩体的剪力V2为：

三角形荷载下任一截面i的剪力V3为：

3 煤帮极限平衡区宽度分析

由图 1可知，在巷帮弹塑性截面上，τ=x0，s=0。由式（4）～式（7）可得弹塑性界面上总的剪应力为：

由应力极限平衡原理可知，当煤帮弹塑性界面上的岩体所受应力达到极限平衡时将产生剪切滑移，然后挤压底板并形成底鼓。

4 巷道底板岩体破坏深度计算

巷道煤帮将顶板支承压力传递给巷道底板的滑移线场模型如图6所示。

图6 巷道底板滑移线场模型

为便于讨论底板破坏深度，建立简化后底板岩体力学分析模型如图7所示。

图7中的两组直线分别为主动极限区aa′b和被动极限区acd的滑移线，而a′c为对数螺线。设底板岩体的内摩擦角为1φ，对数螺线方程为：

图7 巷道底板力学计算模型[11]

由图7可得：

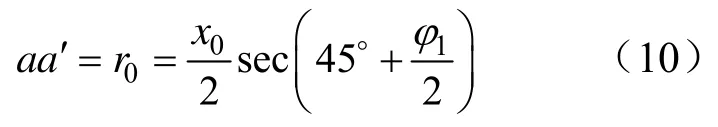
同理，在Δoae中，有：

对于Δdac仍可简化为等腰三角形，其中：

将式（16）代入式（11）即可得到：

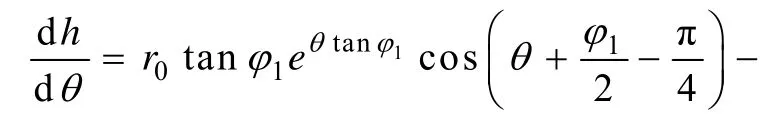
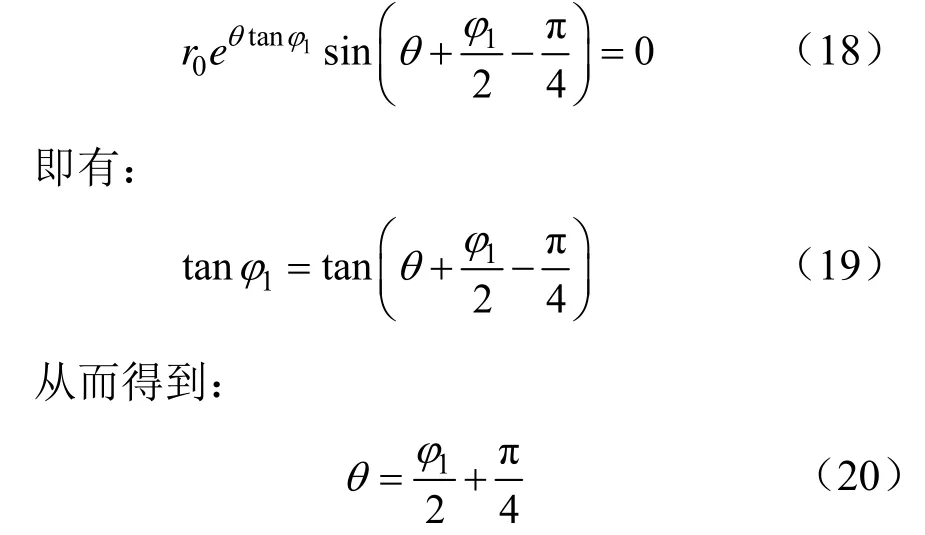
把式（10）和式（20）代入式（17）得到巷道底板岩体最大破坏深度hmax：

此外，利用Δoae还可求得最大破坏深度距煤帮表面的水平距离：

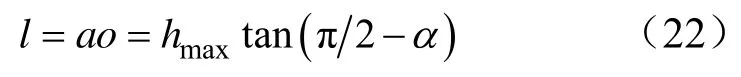
将式（16）和式（20）代入式（22）可得：

5 巷道底板破坏深度计算

5.1 煤帮极限平衡区宽度分析

为有效控制巷道两帮及底板的变形破坏，在此运用式（8）来确定煤帮的极限平衡区范围，将表1中各已知参数代入式（8），并利用matlab数值分析软件求得文家坡煤矿4102运顺1255～1278 m区间段的煤帮极限平衡区宽度为2.95 m。

5.2 巷道底板破坏深度分析

结合上述煤帮极限平衡区的计算结果，当底板岩体内摩擦角φ1=10°时，由式（21）得最大破坏深度hmax为：

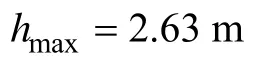
将hmax= 2 .63 m 代入式（23）得最大破坏深度hmax距相应巷道煤帮壁的距离为：

在确定运输顺槽煤帮极限平衡区宽度及底板最大破坏深度的基础上，合理设计锚杆（索）的支护参数并对巷道两帮及底板进行了加固处理。监测结果表明，加固后巷道围岩变形速率显著降低，围岩稳定性得到明显改善。

6 结论

（1）将回采巷道煤帮支承压力的曲线分布形式改为线性分布，建立了回采巷道煤帮的弹性地基梁受力模型。综合考虑极限平衡区和弹性区上方顶板支承压力对煤体变形的影响，给出了煤帮任一界面上的剪力计算方法。

（2）回采巷道两帮煤体在支承压力下塑性流动的实质是煤帮弹塑性界面上煤体所受的剪应力超过其抗剪强度，得到了巷道埋深、顶板上覆岩层容重、煤帮应力集中系数、煤体极限平衡区和弹性区的宽度、回采巷道两帮下底板的弹性特征值及煤体抗剪强度的关系式。

（3）利用上述方法计算了文家坡煤矿4102运顺巷道煤帮极限平衡区宽度和底板破坏深度，为合理确定该巷道围岩支护参数提供了科学可靠的理论依据。