波浪作用下墩柱结构物涂层界面气泡演化规律
常留红,徐 斌,孙文硕,覃甁山,汤 薇
(1.长沙理工大学水利工程学院,湖南 长沙 410114; 2.洞庭湖水环境治理与生态修复湖南省重点实验室,湖南 长沙 410114; 3.中交第二航务工程勘察设计院有限公司,湖北 武汉 430071)
墩柱是近海及海洋工程中常用的一种结构形式,多用于码头和桥梁建设等,往往由单个或一组柱状结构组成。由于墩柱位于浪溅区的部位长期处于干湿交替状态,波浪对结构物的低频往复冲击力加速了结构物的腐蚀破坏[1]。研究表明,涂层的腐蚀失效一般起源于缺陷处[2]。混凝土结构物在涂覆防护涂层过程中,不可避免地会形成小气泡等初始损伤[3-4],而波浪冲击荷载往复作用加剧了涂层界面上气泡等初始损伤的扩展演化,导致结构物涂层剥蚀而提前失效[5]。涂层失效[6-7]是指涂料在使用过程中由于各种原因,导致涂层的物理、化学和机械性能发生不可逆的变化,最终致使涂层的破坏。其中,涂层起泡是由于涂层某一部位与接触物体之间的黏结力降低,造成底材表面升起半球状凸起,这是涂层失效最为常见的表现。可见,波浪冲击荷载作用下涂层界面的气泡损伤演化是涂层防腐性能劣化的重要原因。由于气泡等初始损伤导致涂层剥蚀问题已成为近岸工程防灾减灾亟须解决的热点和难点问题。
为了描述涂层材料的力学特性,有关学者建立了多种本构模型,如黏弹性本构模型和弹性模型[8-9]等。Alice等[10]对全固化和部分固化的矩形环氧树脂试样进行了多温松弛试验,计算了与溶液浓度有关的玻璃化转变温度,考虑了固化程度的影响,从而优化了文中提出的环氧树脂黏弹性本构模型的参数。李勇等[11]根据环氧树脂的流变性质,提出了一种未固化的环氧树脂黏弹性本构模型,并揭示了材料的双牛顿区现象。许珊珊[12]通过对PTFE涂层织物膜材料进行循环拉伸性能、蠕变性能和应力松弛性能的试验,研究了加载次序、温度、应力水平和拉伸速率等因素对涂层织物膜材料黏弹性力学性能的影响规律,并推导了基于各向异性的膜材料黏弹性本构方程。
除了建立黏弹性本构模型外,众多学者还通过建立线弹性本构模型来研究涂层的应力应变行为。HU等[13]将涂层看作简单的弹性模型,并基于弹性分析,预测出高温下陶瓷表面的拉伸应力不会大到足以引起表面裂纹的结论。对比黏塑性本构模型,发现虽然两种模型预测结果存在一定的数值差异,但在基于应力失效机理分析中,黏弹性本构模型预测精度较高。Zhang等[14]根据试验结果分析了温度、压力和应变速率对聚氨酯涂层应力应变行为的影响,建立了温度和应变速率与杨氏模量、屈服应力和应变硬化斜率的关系模型,并提出一个双线性本构模型描述随温度、应变速率和压力变化的应力应变行为,模型预测与试验结果吻合较好。
还有一些学者通过单轴压缩试验研究涂层的应力-应变关系。Handge[15]通过分析剪切滞后模型,研究了单轴荷载作用下聚合物涂层连续开裂过程中碎片尺寸分布的演化规律,阐明了界面非线弹性应力传递机制对断裂动力学的影响,并利用界面剪切应力的非线性表达式,导出涂层应力和应变的解析表达式。黄钰桐等[16]研究了不同养护龄期对环氧树脂-混凝土单轴压缩试验的影响,通过分析环氧树脂-混凝土早龄期的压缩性能,建立了考虑龄期的环氧树脂-混凝土单轴压缩强度预测本构模型。
以上对涂层本构模型的研究成果和试验方法为研究混凝土结构涂层界面气泡损伤演化提供了理论依据。然而在复合材料损伤研究中,在波浪驱动的低频交变应力作用下,涂层界面应力响应过程及损伤演化的相关研究有待进一步深入开展。本文基于ABAQUS软件,通过加载与波浪作用同周期和幅值的等效低频冲击荷载,研究涂层界面气泡在波浪冲击载荷作用下的动力应力响应过程,并将初始损伤引入连续介质模型,分析波浪荷载作用下涂层内部气泡损伤演化过程,以及界面气泡局部细观应力应变场及其演化过程规律,并建立波浪作用下的涂层界面损伤本构模型。
1 数学模型
应用于水利工程的新型环保防护涂层主要有环氧涂层、氟碳防腐涂层及聚脲防腐涂层等。其中,环氧涂层具有突出的黏接、力学和耐介质等性能被广泛应用于海洋防腐中[17]。试验表明,环氧涂料较适用于海洋结构物的浪溅区[18]。因此,选取环氧树脂涂层作为研究对象,应用ABAQUS建立涂层三维数值模型,开展气泡对涂层界面的损伤演化研究。
1.1 线弹性理论
由于环氧涂层涂料与混凝土之间具有良好的附着力,在不考虑化学腐蚀、开裂等其他因素时,波浪力的作用不会导致无损伤处的脱黏,并且由于短时间内气泡不会破裂即不会发生塑性应变,所以只考虑气泡的弹性应变阶段。
线弹性本构方程可表达为
σ=Ddεd
(1)
式中:σ——应力分量向量;d——阶数;Dd——弹性矩阵;εd——应变分量向量。其中,各向同性线弹性模型的应力-应变表达式为
(2)
各项同性线弹性模型的模型参数为弹性模量E和泊松比ν,剪切模量G与E、ν的表达式为
(3)
1.2 数学模型参数及网格划分
通过UG进行建模,ABAQUS导入进行计算。其中,计算模型分为柱状混凝土、涂层、气泡(初始损伤)三部分,柱状混凝土的直径和高度均为2 m;涂层覆盖在圆柱侧表面,涂层厚度对性能的影响较大。试验[19]表明:涂层厚度取值范围应为0.13~0.40 mm,本文取0.30 mm。为便于分析和研究气泡的演变规律,通过增大气泡直径加速气泡的力学变化[20],气泡的水平投影直径取值分别为20 mm、40 mm、60 mm。由于在波高和周期相同的条件下,不同水深的应力谱基本相同,因此为减少计算量,只考虑加载水深为9 m时不同波浪要素下的荷载谱。
环氧涂层材料参数采用文献[21]的数据,海洋浪溅区的混凝土结构较多采用C50等级的海工高性能混凝土,具体参数为:环氧树脂密度为980 kg/m3,弹性模量为2 580 MPa,泊松比为0.37;混凝土(C50)密度为2 500 kg/m3,弹性模量为35 GPa,泊松比为0.2。
对建立的本构模型进行网格自动划分。在网点布种时,要保持各部件的布种点重合,这样模拟计算结果的精度才准确,否则,将导致精度下降,迭代时不收敛,无法完成模拟运算。气泡网格采用C3D8R单元(八结点线性六面体单元),如图1所示,为便于观察,气泡网格放大了50倍。

图1 网格划分Fig.1 Schematic diagram of model meshing
1.3 网格收敛性验证
为确保网格大小设置的合理性,各工况初始网格大小设置为直径的1/30,再增加一组网格大小为直径1/60的工况进行验证计算,对比最大应变值的时间历程。以直径60 mm为例,气泡的网格大小分别为2 mm和1 mm。由于气泡向四周为渐变网格,且渐变区域远大于气泡大小,对应变区域基本无影响,所以结构上下底面的网格大小都设为10 mm。
由图2可知,两种大小网格的计算结果基本相同,所以网格大小设为2 mm(直径的1/30)是合理的。

图2 网格收敛性验证 Fig.2 Grid convergence verification
1.4 应力-应变曲线验证
为验证建模过程的正确性,将通过单轴压缩试验得到的真实应力和塑性应变进行验证,数值模拟的计算条件设置与文献[22]中的物理模型试验条件一致:圆柱试样高30 mm,直径20 mm,弹性模量E=210 GPa2,泊松比ν=0.3。由图3可见,试验曲线和数值模拟曲线吻合良好。
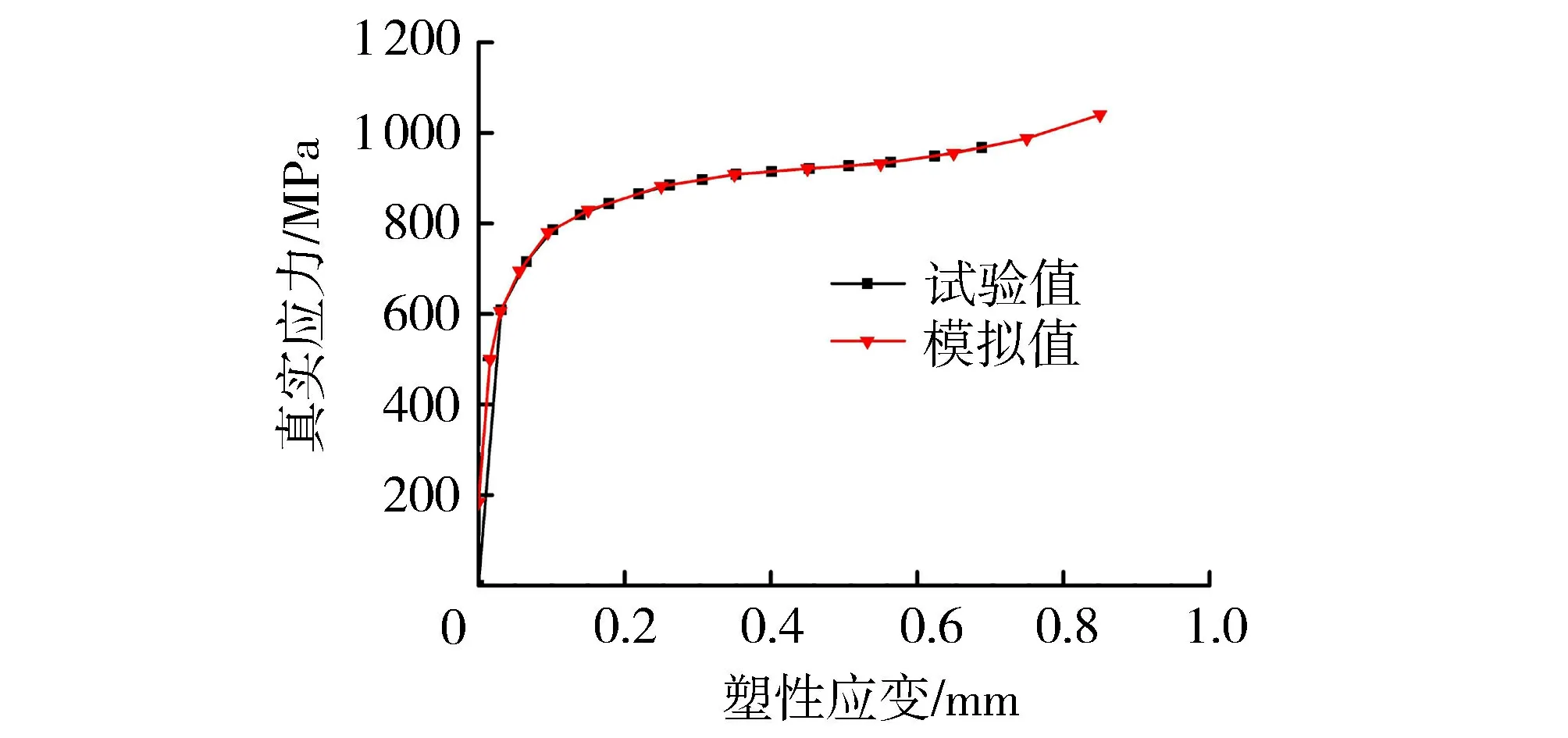
图3 塑性应变验证Fig.3 Plastic strain verification
2 波浪作用下气泡对涂层界面损伤演化机理
结合工况,气泡直径为φ=40 mm、波浪高度为H=1 m、波浪周期为T=4 s的应力和应变历时曲线,分析涂层界面气泡的云图变化及其对波浪力的动态响应。由图4可以看出,气泡最大应变和应力值随时间的变化与水平波浪力基本一致。涂层界面气泡在波峰处应力和应变达到最大,波峰过后,应力和应变随时间逐渐减小,当水面线低于气泡所在位置时波浪与气泡不接触,大约持续1/2T,这段时间内应力和应变不发生变化(即为0)。从图4可以看出,应变和应力均呈周期性变化。
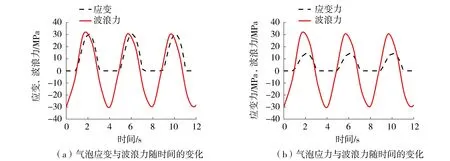
图4 应力、应变和波浪力随时间t的变化Fig.4 Variations of stress,strain and wave force with time
结合图5可知,应变云图在-2.5×10-5~3.1×10-3之间变化,气泡在一个波浪周期内应变先增大后减小,并且中心位置处的应变最大。随着时间的推移,应变范围逐渐扩大,并在t=1/2T时达到最大值,应力峰值为14.37 MPa。通过扩大变形系数可以看出气泡的应变范围和裂缝的扩展方向相互垂直,分别为水平扩展和垂直扩展,气泡变形是从中心位置形成一个竖向裂缝,随着时间的推移(即水平波浪力的变化)继续竖向发展,并向两侧扩展,在t=1/2T时裂缝达到最大。气泡的应变在波峰后逐渐减小,应变范围也逐渐缩小,呈现周期性变化,峰值为3.05 mm。
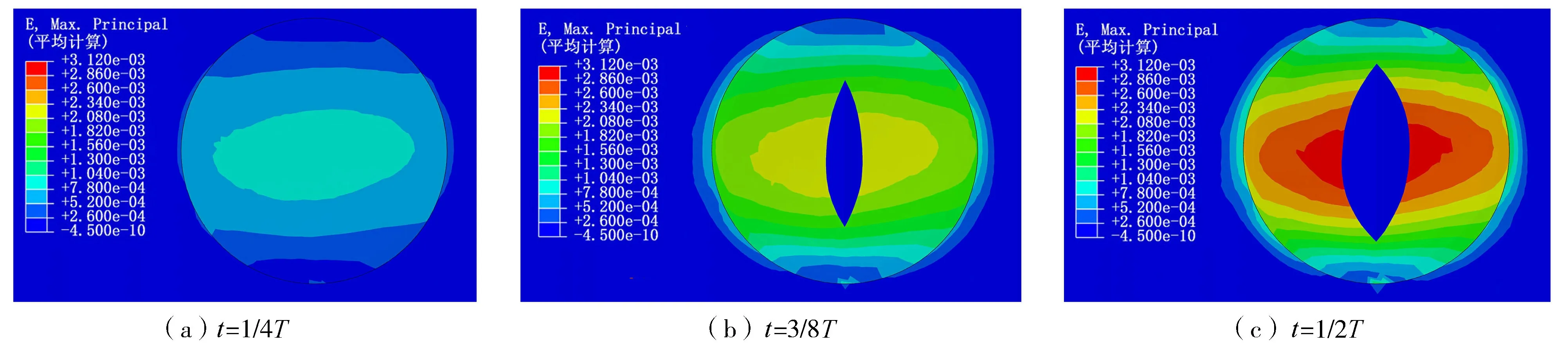
图5 气泡应变随时间变化云图Fig.5 Change of bubble strain nephogram with time
通过波浪作用于气泡的时间历程中气泡应变云图的变化情况,分析不同因素对涂层界面和气泡损伤演化趋势的影响。由分析可知,应变和应力呈周期变化,1/4T时开始产生应变和应力,并随着时间推移逐渐增大,1/2T时应力和应变达到最大。随后,气泡的应力和应变逐渐减小,在3/4T时波浪与气泡开始分离,达到最小值。应力和应变过程变化对称,为减少计算量,主要分析前1/2T气泡应变的变化情况,对比时间为1/4T、3/8T、1/2T时的云图。
2.1 波高对涂层界面气泡应变的影响
选取φ=40 mm、T=4 s的工况,分析H=1 m、1.5 m、2 m时对涂层界面气泡应变的影响。
如图6、图7所示,应变云图在-2.5×10-5~6.5×10-3之间变化。随着波高的增加,各时间点气泡中心位置的应变越大,且等值的应变范围越广,其中应变值最大的区域位于气泡中心,应变值最小的区域位于气泡的上下两侧。气泡横向的应变值分布较广,近似一个椭圆。气泡变形是先从中心位置形成一个竖向裂缝,随着波浪力的增大,继续竖向发展,并向两侧扩展,随着波高的增大,变形越大。另外,气泡的变形发展在初始时竖向变形较大,随着波浪力的增大,横向扩展速度加快,竖向扩展速度减慢。由以上分析可知,在其他条件相同的情况下,气泡的损伤演变随着波高的增大而增大。

图6 t=3/8T时波高对气泡应变影响云图Fig.6 Influence nephogram of wave height on bubble strain at t=3/8T
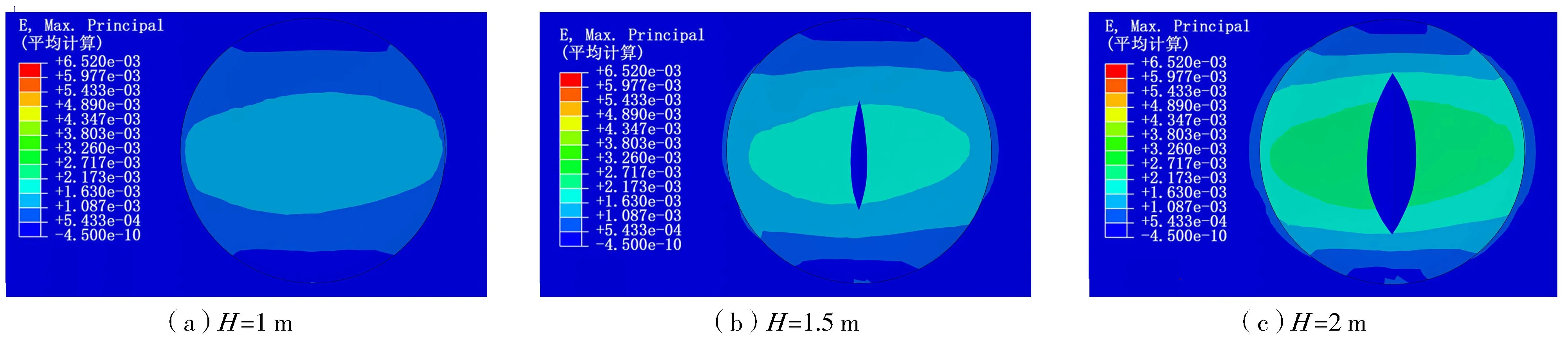
图7 t=1/2T时波高对气泡应变影响云图Fig.7 Influence nephogram of wave height on bubble strain at t=1/2T
2.2 周期对涂层界面气泡应变的影响
选取φ=40 mm、H=1 m的工况,分析T=4 s、6 s、8 s时对涂层界面气泡应变的影响。
由图8、图9可知,应变云图在-2.5×10-5~3.18×10-3之间变化,在不同波浪周期波浪力的作用下,气泡的裂缝在不同时刻略有差异,但其变化过程是相同的,并且裂缝的大小和范围基本相同,但波浪周期越小,波浪力作用的频率越快。由此可见,在其他条件相同的情况下,同一时间内短周期波浪对气泡造成的损伤更大。
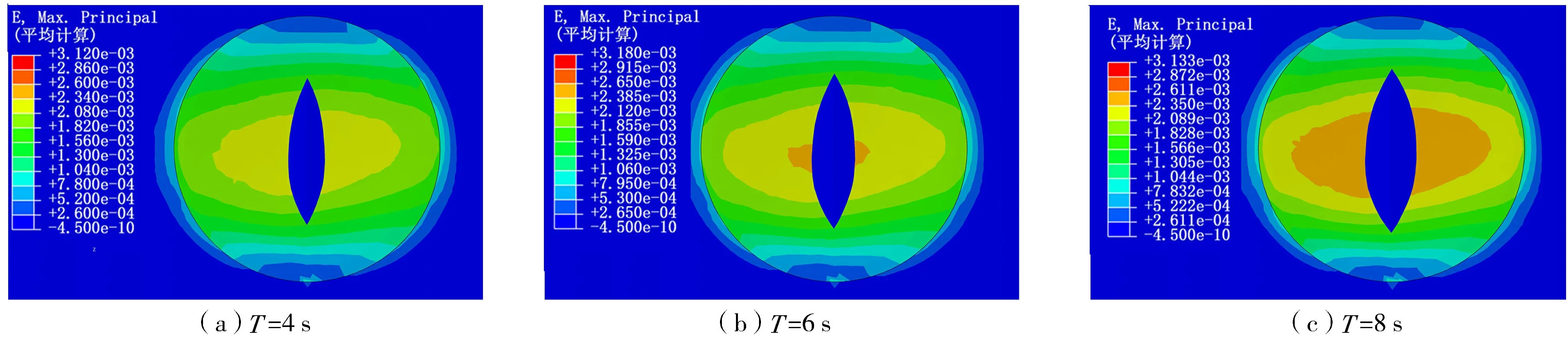
图8 t=3/8T时波浪周期对气泡应变影响云图Fig.8 Influence nephogram of period on bubble strain at t=3/8T

图9 t=1/2T时波浪周期对气泡应变影响云图Fig.9 Influence nephogram of period on bubble strain at t=1/2T
2.3 气泡直径对涂层界面气泡应变的影响
选取工况H=1 m、T=4 s的波浪荷载,分析φ=20 mm、40 mm、60 mm时气泡对涂层界面气泡应变的影响。
由图10、图11可知,应变云图在-4.5×10-5~3.5×10-3之间变化,当波浪周期和波高相同时,在同一时间点,应变的大小随气泡直径的增大而增大,且φ=60 mm的气泡最先出现裂缝。对比图11可以发现,在同一时间点时,气泡直径越大,其裂缝扩展速度越快,范围也越广。由此可知,在其他条件相同的情况下,气泡直径越大,越容易破裂损伤。

图10 t=3/8T时气泡直径对气泡应变影响云图Fig.10 Influence nephogram of diameter on bubble strain at t=3/8T

图11 t=1/2T时气泡直径对气泡应变影响云图Fig.11 Influence nephogram of diameter on bubble strain at t=1/2T
如图10所示,随气泡直径的减小,应变分布(椭圆的形状)越规则。应变在z轴方向从中心向两侧逐渐减小,并且相对于x轴方向递减速度较快,应变最小值位于气泡的上下两端,分布范围也近似于椭圆状。
3 波浪作用下涂层界面气泡最大应变值的变化规律
分析不同因素对涂层界面气泡最大应变值的影响,并通过固定其他变量,对某变量与涂层界面气泡最大应变值的关系进行定性分析。
3.1 波高对涂层界面气泡最大应变值的影响
如图12(a)所示,同一直径的气泡,其最大应变值随波高的增大而增大,3种直径气泡的最大应变值变化规律一致。从不同直径曲线还可以看出,气泡直径的大小虽然差值相同,但直径为60 mm和40 mm的最大应变值变化曲线间距相对于直径为40 mm和20 mm的两条曲线间距较小,可以认为气泡直径越小,涂层界面气泡最大应变值变化越大。
3.2 波浪周期对涂层界面气泡最大应变值的影响
如图12(b)所示,同一直径的气泡,其最大应变值基本不随波浪周期的变化而变化,不同气泡直径的3条曲线近似于水平线,由此可以认为波浪周期对气泡最大应变值的大小没有影响。但从相邻两条曲线的间距可以发现,与波高规律相同,即气泡直径越小,涂层气泡最大应变值变化增大,呈不等间距变化。
3.3 气泡直径对涂层界面气泡最大应变值的影响
由分析可知,气泡直径越小,涂层界面气泡最大应变值变化越大,呈不等间距变化。结合图12(c)可以发现,气泡的最大应变值随直径的增大而增大,但当气泡直径足够大时,应变的变化受气泡直径增大的影响逐渐减小。
3.4 不同因素下涂层界面损伤演化规律
综合波浪高度、周期以及气泡直径各因素,气泡应变随直径和波浪高度变化曲线如图13所示。
由图13可知,应变峰值随气泡直径和波高的增大而增大。应变和气泡直径呈现多项式关系,而应变和波高呈正线性关系,拟合公式为
ε1=α1φ2+α2φ+α3
(4)
ε2=β1H+β2
(5)
式中:ε1、ε2——对应气泡直径和波高的应变;α1、α2、α3——考虑气泡直径的影响系数,β1、β2——考虑波高的影响系数。
将式(4)和式(5)进行拟合,得出应变与气泡直径和波高的经验公式:
ε=-0.837Hφ2+0.115 1Hφ
(6)
由于在弹性应变范围内,T与峰值应变大小无关,但与应变的时间历程有很大的关系,并且应变随时间的变化规律与施加的周期荷载变化情况一致。根据式(6),可得图14。
如图14所示,同一条件下,拟合公式中应变随波高的增大而呈线性增大,随气泡直径的增大而呈多项式增大。当其他条件相同时,波高对涂层界面损伤演化的影响最大;气泡直径对涂层界面损伤演化的影响有限,当气泡直径足够大时,应变的变化受气泡直径增加的影响逐渐减小。因此,通过探索波浪作用过程中结构物/涂层界面的气泡损伤演化过程响应,对延长海洋结构物使用寿命和减小灾害性腐蚀破坏具有重要的理论意义和应用价值。
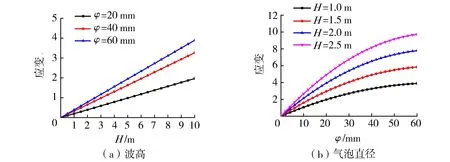
图14 应变随波高和气泡直径的变化曲线Fig.14 Variation curves of strain with wave height and diameter
4 结 论
a.涂层界面气泡中心最先达到应变破坏的临界点,并逐渐向四周扩展。气泡变形是从中心位置竖向演化,并随着波浪力的增大,逐渐竖向发展,同时逐渐向两侧扩展,且随着波高的增大,横向扩展速度加快,竖向扩展速度逐渐减慢。
b.在其他条件相同的情况下,气泡的应变与波高呈线性正相关关系;应变与气泡直径呈二次方正相关关系,但应变速率与气泡直径呈负相关关系;周期对气泡应变没有影响,只影响气泡应变的变化周期。
c.根据应变随波浪要素和气泡直径等参数的变化规律,拟合应变与气泡直径和波高的经验公式。从经验公式曲线图中可以看出,当其他条件相同时,应变的变化受气泡直径增加的影响逐渐减小。

