具脉冲出生和季节性捕杀的种群系统优化算法
黄光球,陆秋琴
西安建筑科技大学 管理学院,西安 710055
非线性规划问题的全局最优解的求解是一个非常困难的问题,因为只有凸规划且其数学表达式可导时,采用传统优化理论才能获得其全局最优解。若非线性规划是非凸非凹或者是其数学表达式不可导,则传统优化理论失效。为了解决该问题,人们发明了群智能优化算法来求取非线性优化问题的全局最优解[1-3]。此类算法对非线性优化问题的结构没有特殊限制条件,因而具有广泛的适应性。
传统的群智能优化算法是依据一些特殊的自然现象构造而得,自然现象本身的特征对群智能优化算法的性能影响很大。因此,寻找具有优良特性的自然现象来构造群智能优化算法是提升群智能优化算法的有效手段。最近几年,人们已提出了很多新型的群智能优化算法,如蝙蝠算法[4]、蜂群算法[5]、鲸鱼算法[6]、蛙跳算法[7]、灰狼算法[8]、布谷鸟算法[9]等,这些算法的共同特征是算法所依据的自然现象非常简单,无法用数学模型进行描述。由于存在此缺陷,关于算法的参数确定和性能分析变得异常困难。
为了解决上述问题,人们开始寻求能被数学模型很好描述的自然现象来开发新一代群智能优化算法,其中能够被种群动力学数学模型[10-11]描述的自然现象就是其中的一种。文献[12]采用两个种群Lotka-Volterra 种群动力学模型构建出了第一个种群动力学算法,种群间的作用关系有竞争、互利、捕食-被食、融合、突变和选择;以文献[12]为基础,文献[13]构建出了基于3 个种群的Lotka-Volterra 种群动力学优化算法。
在自然界中,很多种群的增长是通过脉冲出生新生个体来完成的,一段时间后,从幼年种群成长而来的成年种群的捕获也是季节性的。该自然现象非常普遍,且能被具脉冲出生和季节性捕杀的种群动力学数学模型[14-15]很好描述。本文正是依据该自然现象构造出了一种新的群智能优化算法——具脉冲出生和季节性捕杀的种群系统优化算法(population system optimization with impulsive birth and seasonal killing,PSO-IBSK)。与现有的种群动力学优化算法相比,本文算法具有如下特点:
(1)种群个体自然地划分成幼年个体(简称幼体)和成年个体(简称成体)两类,每类个体数是依据具脉冲出生和季节性捕杀的种群动力学模型自动进行动态计算而得,避免了人工确定个体数的困难。
(2)所有算子是通过幼体的脉冲出生、幼体演变为成体、成体的季节性捕杀、虚弱个体的死亡而构造出来的,符合种群动力学规律,且与所求解的实际优化问题无关,故具有很好的普适性。
(3)每个算子具有明确功能,其中出生算子和成长算子可分别实现成体向幼体瞬时和延迟传递信息,有助于搜索跳出局部陷阱;捕杀算子可周期性地将不良成体清除,死亡算子可将虚弱个体随机清除,该两个算子有利于提升算法的求精能力;强势算子可实现强壮个体向虚弱个体扩散强壮信息,竞争算子可实现幼年和成体之间的有效信息交换,该两个算子有利于提升算法的探索能力;进化算子可确保算法具有全局收敛性。
(4)采用具脉冲出生和季节性捕杀的种群动力学模型确定PSO-IBSK 算法中的相关参数,使算法的参数确定具有科学性。
(5)计算过程中,PSO-IBSK 算法每次只处理个体特征数的6‰~8%,从而使时间复杂度大幅降低。
1 PSO-IBSK 算法设计方法
假设要求解的优化问题如下:

式中,X=(x1,x2,…,xn)为变量,在求解过程中X的不同取值称为试探解,Rn是n维欧氏空间;f(X)为目标函数;H为搜索空间。
1.1 优化问题试探解的生物学解释
在一个生态系统G中生活着一个生物种群,该种群由具有两种阶段状态的若干生物个体组成,即阶段状态s=1 的幼体和阶段状态s=2 的成体,其中幼体经过一段时间的生长后会长大成为成体,而幼体是由成体出生的,幼体的出生持续时间很短,故称之为脉冲出生。为了节省资源,降低种群中的个体密度,需要周期性(季节性)地对该生态系统中一些生长状况不良的成体进行捕杀,以便提升种群的整体质量。
在时期t,假设该种群的幼体数和成体数分别为N1(t)和N2(t),个体总数为N(t)=N1(t)+N2(t);每个幼体和每个成体都用唯一编号表示,于是所有幼体和所有成体的编号集合分别为种群中的每个幼体和每个成体都具有n个特征,于是对于阶段状态为s的个体i来说,用其特征表示就是,其中就是阶段状态为s的个体i的第j个特征,i∈Cs(t),j=1~n,s=1~2。
搜索空间H中优化问题式(1)的试探解与生态系统G中种群的幼体和成体的对应关系如下所述。
时期t,在式(1)的搜索空间H中随机生成N(t)个试探解,即∈Cs(t),s=1~2},其中。将搜索空间H视为生态系统G,则时期t在生态系统G中阶段状态为s的个体i就与搜索空间H中的试探解一一对应,也就是阶段状态为s的个体i的特征与试探解的分量相对应。在生态系统G中,生物个体的动力学演化规律总结如下:
(1)幼体是由成体以脉冲方法突然产生的;
(2)幼体经过时间段T后成长为成体;
(3)在某个季节内,某些生长状况不良的成体会被捕杀掉;
(4)某些虚弱的幼体和成体会死亡;
(5)幼体和成体的生长状况越好,继续生存下去的概率会越高,即个体的演化规律符合达尔文进化论规律。
个体的生长状况由优化问题式(1)的目标函数值描述,个体的生长状况越好,其对应的目标函数值就越小。时期t阶段状态为s的个体i的生长状况用IGI(individual growth index)指数来表示,其计算方法为:
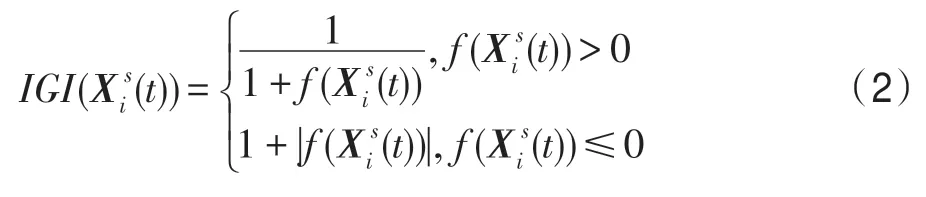
1.2 种群系统动力学模型
在生态系统G中,假设幼体的出生具有规则脉冲性,则具有阶段结构和脉冲出生的单种群离散模型为[16]:
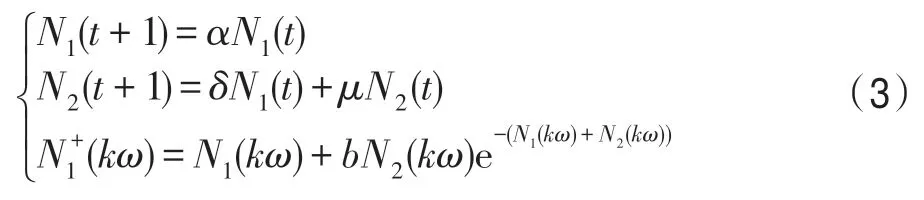
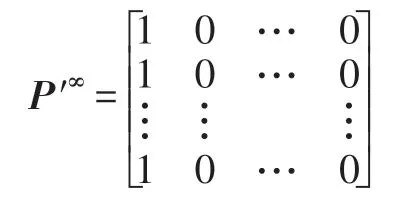
其中,t∈Z+,Z+为非负整数集;令从t到t+1 的幼体的出生数=0,b>0,当t=kω(k∈Z+,ω为正数)时,幼体数N1(t)增加了N2(t);δ为幼年种群的成长率,0<δ<1;幼年和成年的死亡率分别为d1和d2,0 若考虑对成体的捕杀,E为对成体进行捕杀的捕杀率,0 考虑脉冲出生,并考虑对式(4)的成体进行季节性捕杀,不失一般性,设对成体的捕杀发生在(T1/ω,T2/ω](0 ≤T1 迭代N1(t)和N2(t),可得式(5)在脉冲区间内的解析解,即: 式(6)在脉冲区间成立且α≠μ,α≠β。为简单起见,下面总是设α≠μ,α≠β。当t=(m+1)ω时,由式(6)得: 定义内禀再生数R0为R0=bp/(1-r)(1-q),令b0=(1-r)(1-q)/p。当R0<1 时,如果在平均数量上,个体在死亡前没有得到替补和补充,则种群会走向灭绝。式(8)满足: 当R0>1 时,存在一个正平衡点E*(u*,v*),其中: 定理1[17]令γ=若b>b0,则式(8)存在一个正不动点E*(u*,v*) ;若b0 PSO-IBSK 算法的算子是通过各生物个体及其相互之间的作用关系构造而成。令: (1)出生算子。该算子描述的是由成体产生幼体。首先生成阶段状态为s的强壮个体集合SIs(t),该集合中的个体的IGI 指数高于同一阶段状态的IGI 指数的平均值,SIs(t)集合中的个体数为L,L称为特征个体数;然后,从SI2(t)中随机选出两个成体i1和i2,由其产生的幼体数为B(t+1)个,B(t+1)=,即: 式中,i=1~B(t+1) ;MF(t) 为从{1,2,…,n} 中以概率Z0随机选择所形成的特征编号集合;Z0称为个体特征受影响的最大概率;λ=Rand(-1,1),Rand()为均匀分布随机取值函数;ρ=Rand(0,1)。 由式(11)产生的B(t+1) 个幼体的编号集合为BI(t+1)={i0,i0+1,…,i0+B(t+1)-1},i0=|C2(t)|+1。 一方面,因幼体是通过两个强壮个体杂交产生的,故幼体的质量普通较高;另一方面,因幼体是瞬时产生的,故一定数量的优质个体的瞬时投放有助于搜索跳出局部最优解陷阱。 (2)成长算子。该算子描述的是幼体经过一段时间后长大为成体。假设当前幼体i以概率δ要转变为一个成体,为了使该幼体具有成体的一些特征,首先,在阶段状态为s的个体中随机选择L个个体,由其编号形成的集合为GIs(t),然后,将GI2(t)中的成体的部分特征传给该幼体,使其成为成体,即: 然后,将幼体i从幼体集合中删除,即C1(t+1)=C1(t)-{i},将该个体的阶段状态改为成年状态,其编号为|C2(t)|+1,即C2(t+1)=C2(t)+{|C2(t)|+1}。 成长算子描述了质量较高的幼体演变为成体的过程。成体是由高质量的幼体演变而来,若成体的质量不断得到提升,则意味着搜索向全局最优解不断靠近;若成体质量没得到提升,则会被死亡算子和捕杀算子清除掉。因此,在这两个算子辅佐下,成长算子有利于提升本算法的全局寻优能力。 (3)捕杀算子。该算子描述的是将生长状态不良的成体进行人为删除,删除数目为E个。从成体集合选择IGI 指数最低的E个个体,其编号形成的集合为WI2(t),将WI2(t)中的所有个体进行人为清除: (4)死亡算子。该算子描述的是虚弱个体的自然死亡。对当前阶段状态为s的个体i,若该个体的IGI 指数低于处于该阶段状态的个体平均IGI 指数,则以概率ds令其死亡,即: (5)强势算子。该算子描述的是强壮个体的特征向虚弱个体扩散的现象,即强壮的个体对虚弱的个体产生影响。对阶段状态为s,个体编号为i的当前个体来说,有: (6)竞争算子。该算子描述的是幼年和成体之间的相互竞争现象。对阶段状态为s,个体编号为i的当前个体来说,有: (7)进化算子。该算子描述的是个体的进化需满足达尔文进化论规律。对于阶段状态为s的当前个体i,其进化算子的定义如下: 式中,函数IGI()按式(2)计算。 算法1PSO-IBSK 步骤1初始化: (1)令演化时期数G=105~108,误差要求ε=10-5~10-10,L,Z0;N1(0)=N2(0)=200,m=0。 (2)依据2.1 节确定参数b、δ、d1、d2、ω、T1、T2。 (3)在搜索空间H中随机生成试探解集: (4)确定个体编号集合C1(0)={1,2,…,N1(0)},C2(0)={1,2,…,N2(0)}。 (5)以X(0)为基础,找出初始全局最优解Y*0。 步骤2执行下列操作: 步骤3结束。 1.5.1 时间复杂度 PSO-IBSK 算法的时间复杂度计算如表1 所示,其中 1.5.2 PSO-IBSK 算法的全局收敛性分析 Table 1 Time complexity表1 时间复杂度 不失一般性,令f1即为所求的全局最优解。由式(18)的下标形成的集合为U={1,2,…,Z(t)}。 ∀X∈H,有f1≤f(X)≤fZ(t),将H划分为如下非空子集={X|X∈H且f(X)=fi},i=1~Z(t),显然有: 令Xi,j(i=1~Z(t),j=1~表示中的第j个状态;个体从状态(i,j) 转移到状态(k,l) 表示为Xi,j→Xk,l;设pij,kl、pij,k为从Xi,j分别到Xk,l、中任一状态的转移概率,pi,k为从中任一状态到中任一状态的转移概率,则: 引理1在PSO-IBSK 算法中,,i=1~Z(t),j=,满足: (1)引理式(20)的证明:设状态i为时期t个体i的状态,其空间位置为,由式(17)知,该个体具有适应度递增特性,故在时期t+1 有: (2)引理式(21)的证明:设状态i为时期t个体i的状态,在时期t+1,个体i随机选各算子进行演化以便转移到更好的状态k上。此时,存在有如下两种情况: ①若状态i=1,即全局最优状态,因下一步不会转移到较差的状态上去,故必以概率p1,1=1 留在原状态i上。因p1,1=1>0。命题得证。 ②若状态i≠1,则在状态1 和当前状态i之间必至少存在一个中间状态k,使得f1≤fk 综上所述,可得∃k 定理2[18]设P′是一n阶可归约随机矩阵,即通过相同的行和列变换后可得到,其中C是m阶本原随机矩阵,且T≠0,R≠0,则有: 上述矩阵是一个稳定随机矩阵,P′∞=1′P′∞,P′∞=P′0P′∞唯一确定且与初始分布无关,P′∞满足条件: 定理3PSO-IBSK 算法具有全局收敛性。 证明从各算子的定义式(11)~式(16)可知,与满足关系,表明PSO-IBSK算法的演变过程具有Markov特性。每个,i=1~Z(t)是有限Markov 链上的一个状态,根据式(20)可得状态转移矩阵为: 且P′的每行均满足式(19)。根据式(21)可得: 于是,P′是一个Z(t)阶可归约随机矩阵,满足定理2 的条件,故有: 因C∞=C=(1),T∞=0,故必有R∞=(1,1,…,1)T,于是: 上式表明,当k→∞时,pi,1=1,i=1~Z(t),于是: 因此,PSO-IBSK 算法具有全局收敛性,证毕。 目前,进行群智能算法收敛性分析的方法有图搜索法[19]、代数方法、解析分析法、状态空间模型法和马尔科夫分析法[20]等,这些方法的证明过程复杂,仅适合于特定算法的收敛性分析,没有通用性。本文提出的群智能算法收敛性分析法是基于有限马尔科夫链的可归约随机矩阵稳定性定理,证明过程非常简单,可适用于所有群智能算法的收敛性分析,具有通用性。同时,本证明过程表明,对一个群智能算法来说,只要其种群个体演化符合达尔文进化论规律,该群智能算法就是全局收敛的。 种群系统模型的参数是算法的内置参数,由1.2节介绍的理论进行设置,用户无需修改。下面讨论这些参数的设置方法。 首先讨论捕杀时间T1和T2选取对式(9)描述的幼年和成体数量的影响,以及种群最大可持续捕杀量E。由定理1 可知,式(9)的正平衡点依赖于收获的时间,尽管捕杀量E相同,太迟的捕杀将导致种群的灭绝。在每个繁殖季节后,收获成体越早,系统可承受的捕杀量越大,对生存下来的个体来说,其存活的概率也越大。从生物学角度来看,捕杀成体可以减少种内竞争,使得其他个体得到充足的食物和空间,进而增加存活概率。因此,在繁殖季节结束后,收获成体对具有脉冲出生的种群是比较有利的。同时也可得到成年种群的平衡态v*是关于T1的减函数。事实上,如果τ为一常数,则: 由于0 由定理1 知,若b0 因此,只需考虑一个周期内的可持续捕杀量。不失一般性,取m=0,则可持续捕杀量为: Fig.1 Changes of the number of juveniles and adults with time图1 幼年和成体数随时间的演变规律 人工控制参数包括Z0和L,需要用户根据所求优化问题的实际特征进行人工设置。下面通过Awad等人最新发布的智能优化算法测试包中所介绍的基准函数F6[21],该函数由Scaffer 函数经旋转和平移扩展而得,其表达式如下:式中,M为n×n维旋转矩阵;O为n维向量,其中每一维的值在[-80,80]中随机选取。 令n=50,Z0=0.01,G=108,PSO-IBSK 算法运行100 次,表2 描述了L与最优目标函数值的平均值(OFV)和计算时间的平均值(CT)之间的关系。表2 表明,当L=3~7 时,OFV的精度达到最佳,而CT递增不大,建议L=3~7。 Table 2 Relationship of L with OFV and CT表2 L 与OFV 和CT 之间的关系 令n=50,L=3,G=108,PSO-IBSK 算法运行100 次,表3 描述了Z0、OFV和CT之间的关系。结果表明,当Z0=0.006~0.080 时,OFV精度较高,但CT增加不大,建议Z0=0.006~0.080。 Table 3 Relationship of Z0 with OFV and CT表3 Z0 与OFV 和CT 之间的关系 本文选用CEC2013[22]智能优化算法测试包中12个难度很大优化问题来对PSO-IBSK 算法与其他算法进行比较,如表4 所示。 Table 4 12 benchmark functions in CEC2013表4 12 个CEC2013 基准函数优化问题 求解这些优化问题时,PSO-IBSK 算法的参数设置是n=50,G=108,ε=10-8,Z0=0.01,M=3。与PSOIBSK 算法进行比较的7 种智能优化算法为BRKGA(biased random-key genetic algorithm)[23]、ACO-IM(ant colony optimization-influence maximization)[24]、SRPSO(self-regulating particle swarm optimization)[25]、SLIWBBO(self learned invasive weed-mixed biogeography based optimization)[26]、DE-DMSC(differential evolution with dual mutation strategies collaboration)[27],DARSRWO(double adaptive random spare reinforced whale optimization)[28]、GABC(genetic artificial bee colony)[29],这些算法各参数设置可参见其对应文献。 求解各个优化问题时,每个算法均独立求解51次。表5 给出了各算法的求解结果,表中计算结果是各算法求解各优化问题时的计算值与理论值之间的偏差。 Table 5 Results obtained by each algorithm表5 各算法的求解结果 Fig.2 Sample convergence curves图2 样本收敛曲线 从表5 可以看出,这8 个算法按最终排名1 和最终排名2 排序所得的结果均如下: PSO-IBSK>DARSR-WO>DE-DMSC>BRKGA>ACO-IM=GABC>SRPSO>SLIW-BBO 图2(a)~(f)给出了各算法求解优化问题F3、F7、F14、F20、F22、F23 时的样本收敛曲线。 本文基于具脉冲出生和季节性捕杀的种群动力学模型提出的PSO-IBSK 算法能够动态自动计算幼年和成体数,从而使得种群个体数的确定具有科学性;PSO-IBSK 算法中的算子是依据幼体的脉冲出生、成体的长成和季节性捕杀、个体间的竞争关系和虚弱个体的死亡而构造出来的,符合种群动力学规律。各个算子分工明确,个体间信息交换充分,出生算子和成长算子的综合作用有助于搜索跳出局部最优解陷阱,强势算子和竞争算子的综合作用有利于提升算法的求精能力和探索能力,而进化算子能确保算法具有全局收敛性。PSO-IBSK 算法中的大量参数采用具脉冲出生和季节性捕杀的种群动力学模型确定,提升了算法参数确定的合理性和科学性。PSO-IBSK 算法每次处理的个体特征数很少,适应于求解维数较高的优化问题。 PSO-IBSK 算法的下一步改进方向如下: (1)深入研究各算子的动态特征; (2)深入研究个体的动态特征。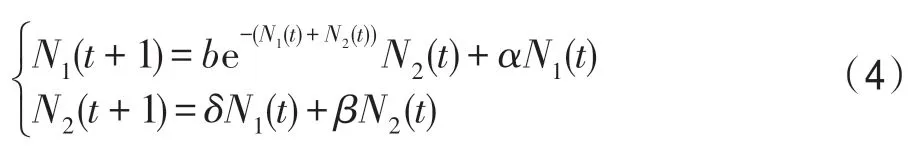


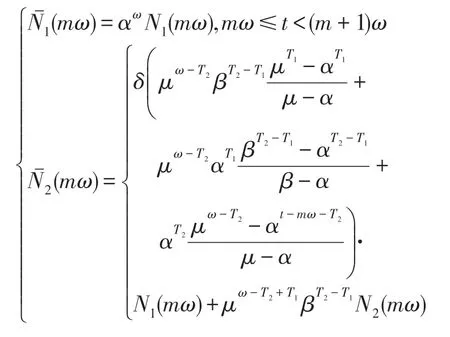
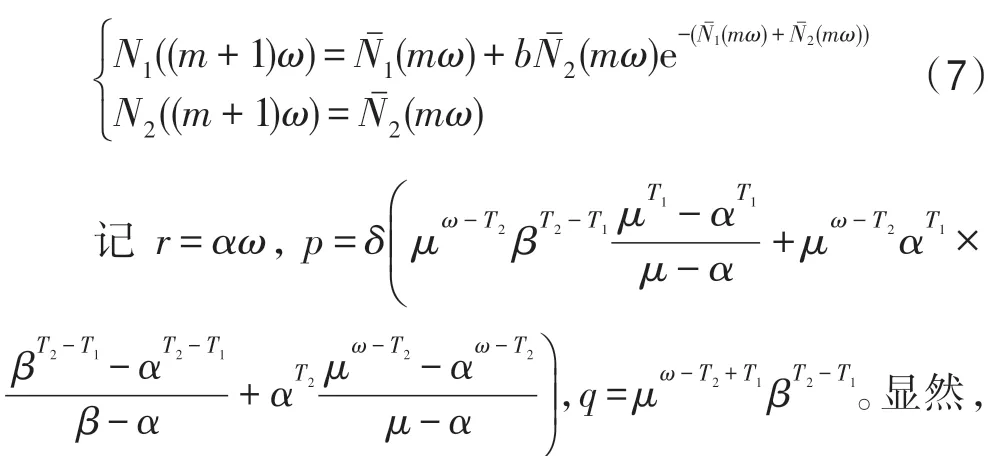
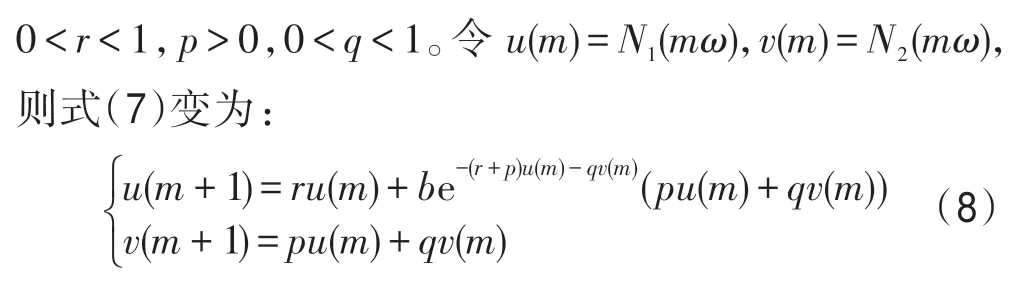
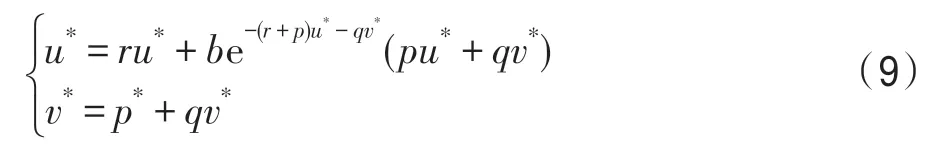
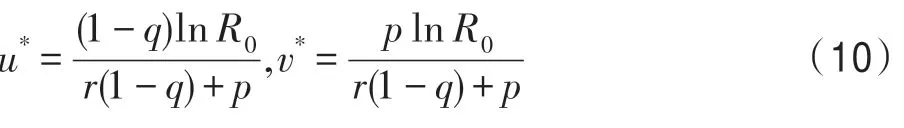
1.3 算子设计
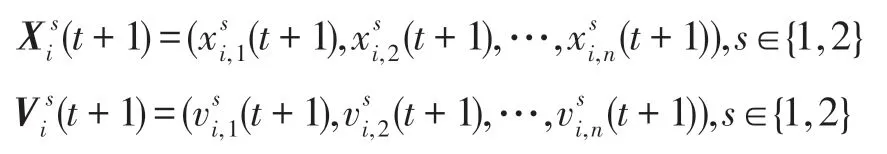
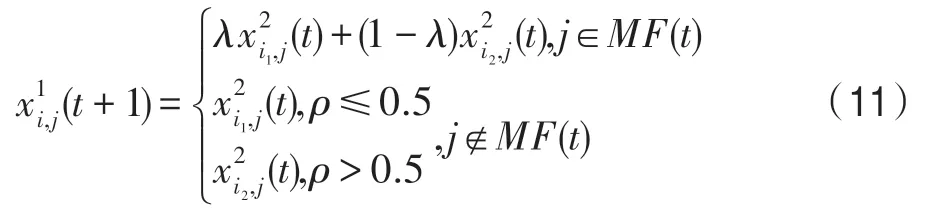
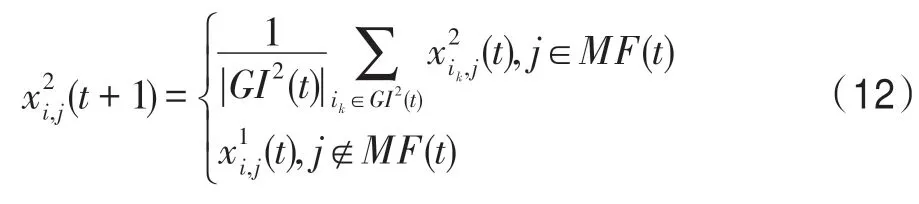



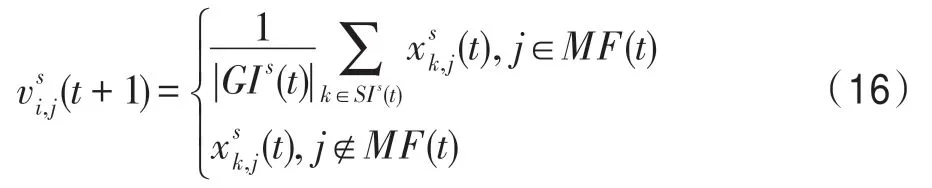

1.4 PSO-IBSK 算法构造



1.5 算法特点分析




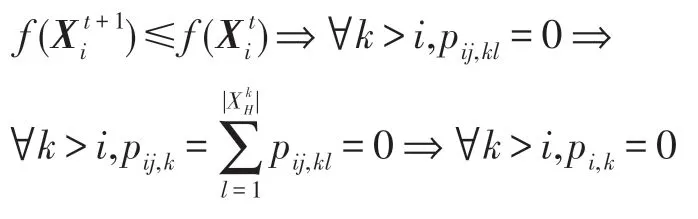
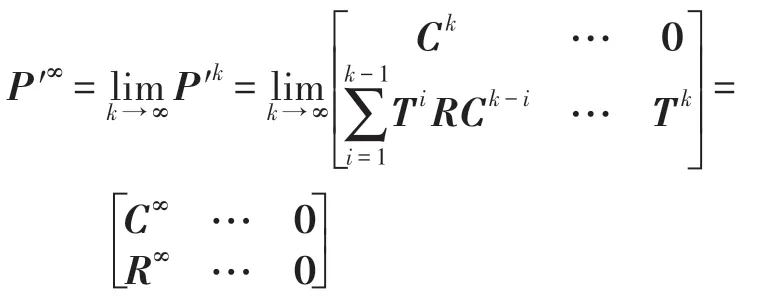
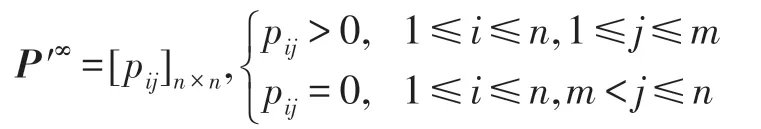


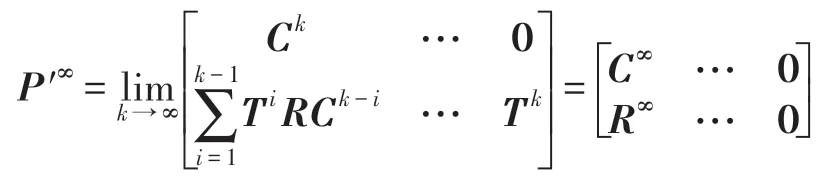
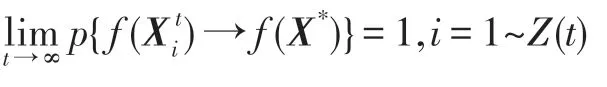
2 算法参数确定
2.1 种群系统模型的参数设置方法


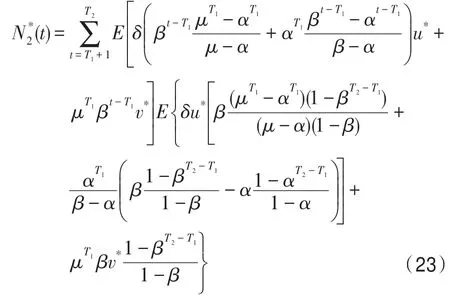

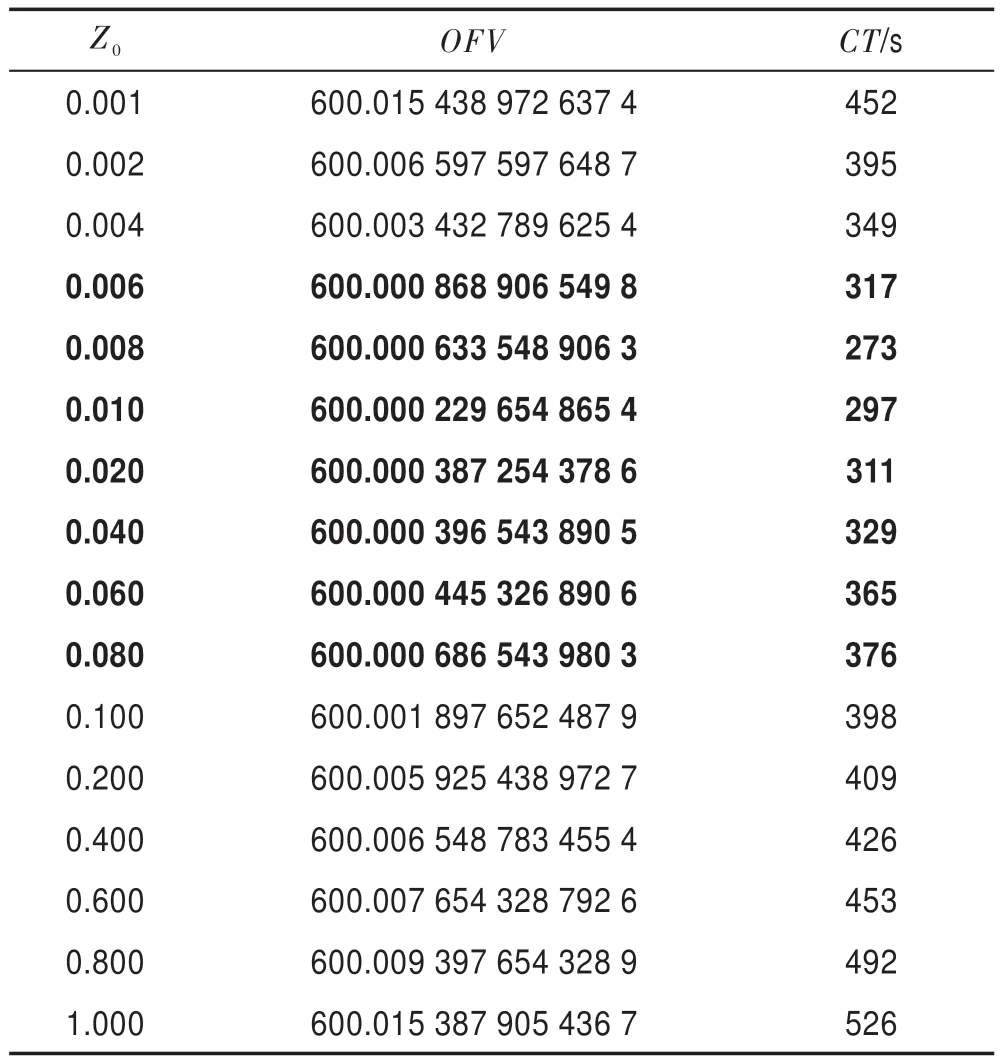
2.2 人工控制参数设置方法
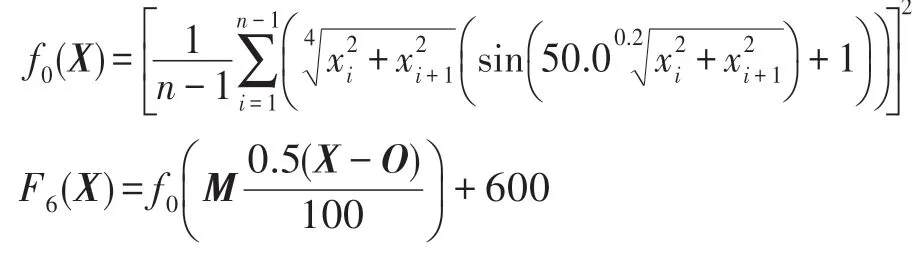

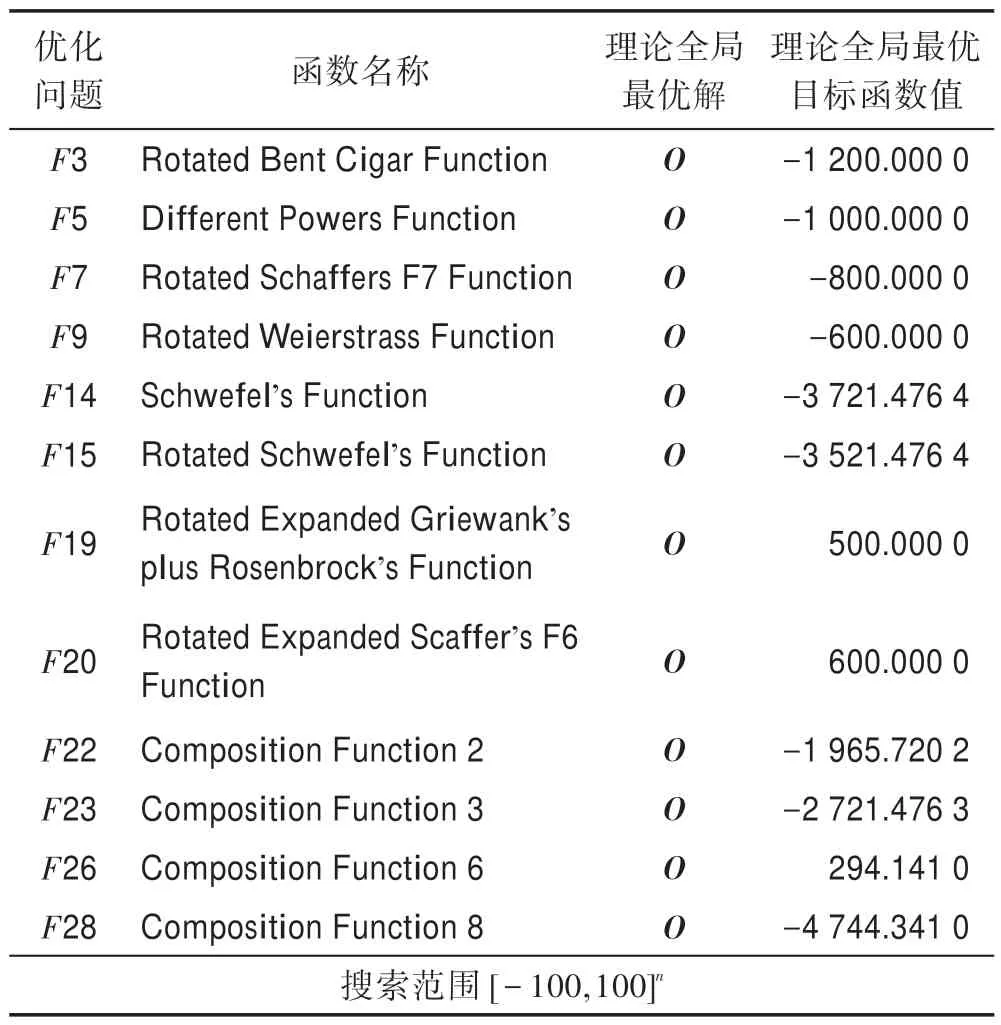
3 PSO-IBSK 算法与其他算法的比较
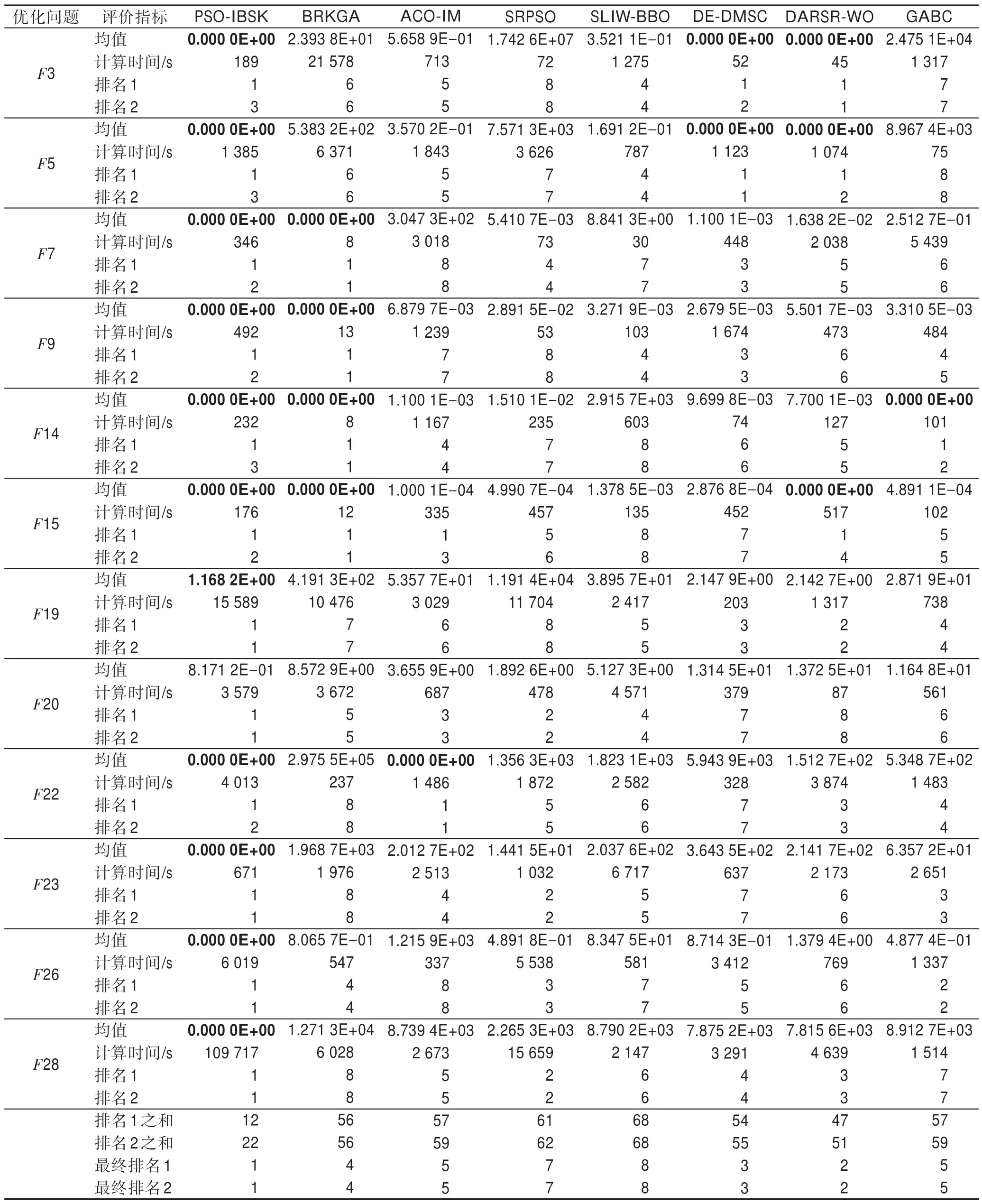
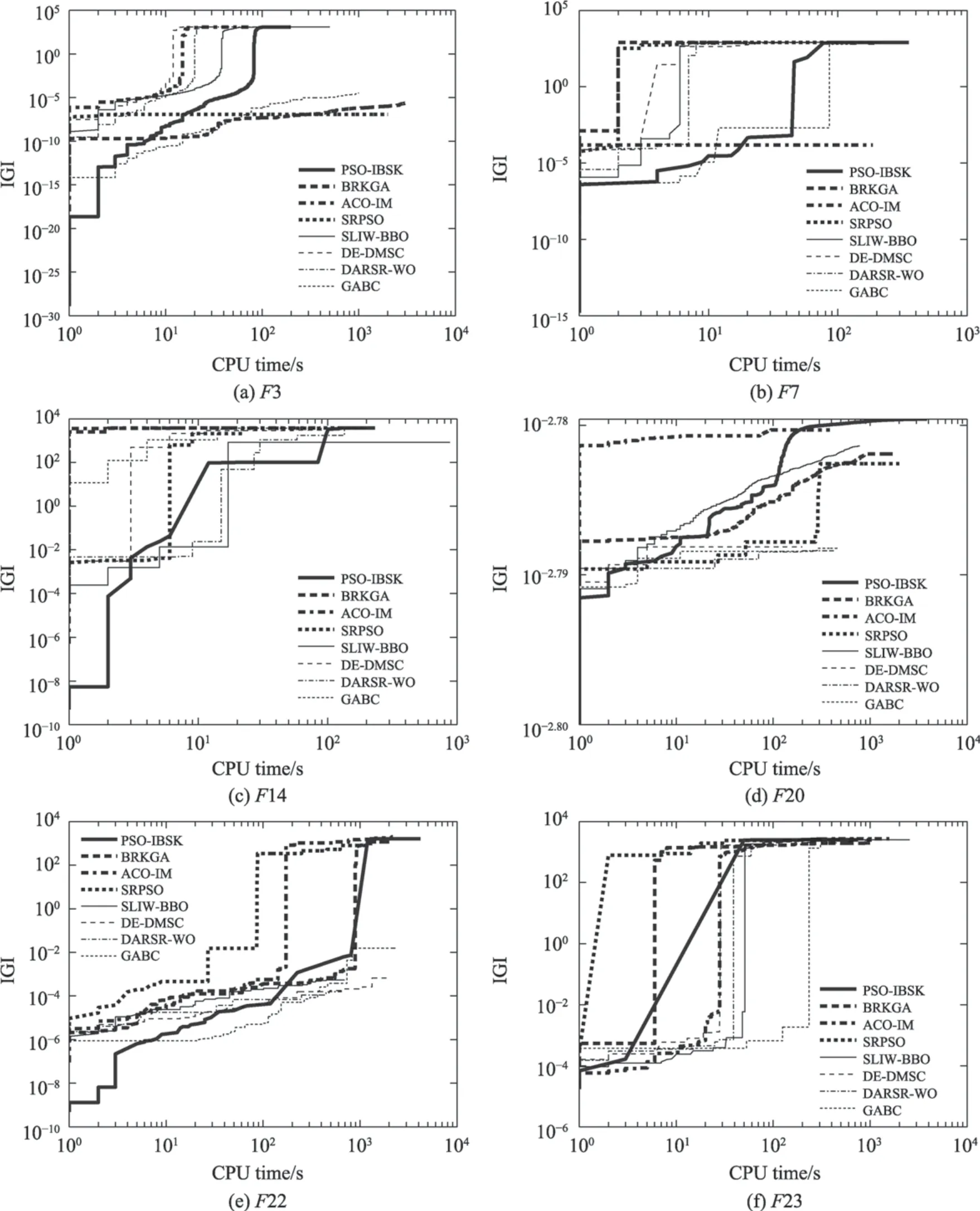
4 结束语

