某水闸结构抗震能力分析

邹国华,周清勇,万亮亮

(1.江西省修江水利电力勘察设计有限责任公司鄱阳分公司，江西 鄱阳 333100；2.江西省水利科学院，南昌 330029)

水闸工程是我国河湖防洪体系中的重要组成部分，但因为建设时期的历史原因和技术条件落后，自然灾害的影响以及后期维护不足，大量水闸结构存在各类安全隐患。在2009年的全国大中型水闸专项除险加固规划成果中明确指出，当年我国的2 622座大中型水闸中，有184座存在结构抗震能力不满足规范要求的情况，能否安全运行关乎当地人民的生命财产安全[1]。目前为止全世界仅日本方面对水闸抗震性能开展了系统研究[2-3]，我国多数水工结构抗震性能分析集中于探索混凝土坝的抗震能力，少数关于水闸的研究也将重点放在动水-闸门相互作用上，而少有关注水闸结构自身抗震性能[4-8]。因此，有必要对我国处于地震高发地区的水闸工程进行结构抗震能力计算。

1 工程概况

某水闸工程主要由闸室、消能设施和两岸连接段等结构组成，共分3孔，孔口尺寸为12 m×6 m(宽×高)。闸室过流总净宽为36.0 m，总宽为48.0 m(含右岸刺墙)，顺流向全长为48 m。某水闸闸室采用整体式结构，在每个闸孔底板中心线上设结构缝，每个闸室单元呈倒“T”形，横向宽度为14.0 m，闸室顺流向长为25.0 m。闸底板厚为1.5 m，闸墩厚为2.0 m，墩高为16.68 m，胸墙采用板梁式结构，一端与闸墩固结，另一端与闸墩简支，净宽为12.0 m，高为6.93 m，板厚为0.25 m，底梁宽为1.20 m(竖向)，高为2.00 m(水平向)，中梁宽为1.10 m，高为1.60 m。闸门采用弧形钢闸门，半径为10.0 m，弧形闸门支座牛腿高为2.50 m，宽为2.00 m，厚为1.20 m。在弧形门底坎下游侧的闸底板分缝处及防渗铺盖的分缝均设有止水，并与弧形门底坎止水相联。

根据实际工程尺寸建立某水闸有限元仿真模型(如图1所示)，在闸体部分易损区域将网格做细化处理，并建立薄层单元模拟建基面，地基范围按不同方向各取1.5倍闸高。模型共有节点数为120 768个，单元数为86 282个，模型全部单元采用八节点六面体单元，由于水闸结构闸墩上的公路桥、启闭机房是相对独立的，与闸墩上的垫座并无一体化的刚性连接，因此，在公路桥与闸墩和启闭机房与闸墩之间分别设置了薄层单元，体现结构连接处的性能差异。

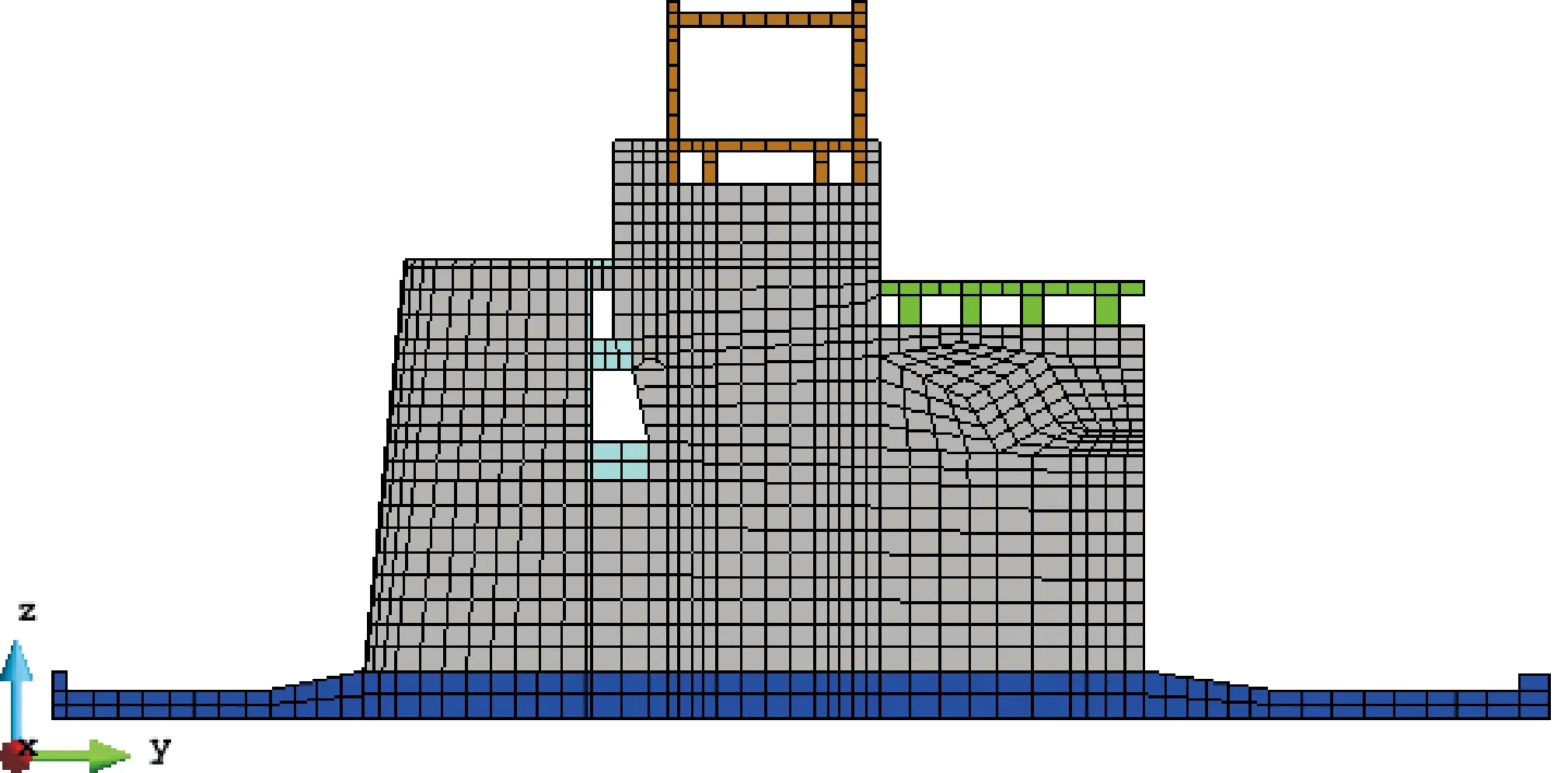
图1 某闸坝有限元模型示意

2 计算参数及仿真理论

2.1 材料参数

模型按业主提供的竣工图纸进行材料分区，由于缺少材料力学性能参数的相关资料，本次仿真计算材料参数按照设计报告结合《水工混凝土结构设计规范》(SL 191—2008)[9]混凝土标号建议值进行取值(见表1所示)。其中材料动态参数在静态情况下根据水工建筑物抗震设计规范(GB 51247—2018)[10]将弹性模量提升50%，抗压强度提升10%。

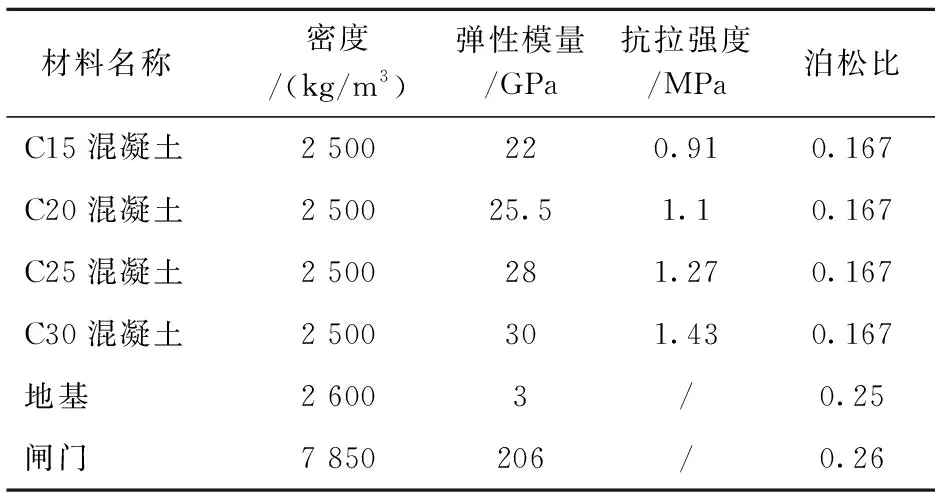
表1 材料参数

2.2 边界条件及荷载组合

本次仿真计算在模型水平向施加法向约束，地基底部施加三向约束，潜在张开、滑移块体部位不施加约束。静力计算荷载包括结构自重荷载、静水荷载、扬压力、土压力、公路桥荷载和启闭机荷载，其中，静水压力主要为闸前14.28 m校核水位时的水推力，公路桥荷载按《公路桥涵设计通用规范》(JTGD 60—2015)规定中二级公路标准进行计算。采用时程法在静力分析的基础上进行动力分析，通过广义Newmark法确定每一时刻坝体与地基的应力分布及变形情况。地震荷载选用Koyna实测波进行计算，按地震动加速度峰值与速度峰值之比A/V可将其分类为高频波，属于对结构较为不利的地震荷载，其归一化的加速度时程曲线如图2所示，采用固定人工边界作为地基边界条件，采用Westgaard附加质量法考虑地震荷载作用下库水—闸体的动力相互作用。使用超载法将输入的地震动荷载按比例放大，对某水闸结构的极限抗震能力作出评价。

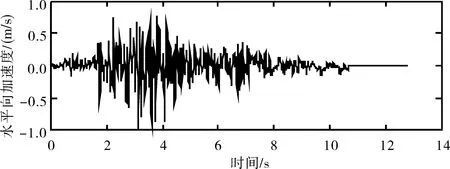
图2 Koyna地震波加速度时程曲线示意

2.3 仿真理论及仿真条件

本文采用通过Fortran语言自主研发的有限元仿真软件，其损伤计算基于应变等效原理，将复杂的多轴问题转换为简单的单轴问题，再通过试验得出的应力应变全曲线计算相应损伤值。根据混凝土的拉压异性，本文损伤模型选取过镇海提出的应力应变全曲线[11]，该曲线已得到国内外科研工作者的认可，并纳入我国混凝土结构设计规范[12]。

混凝土单轴受拉应力应变曲线表达式如下：

σ=(1-dt)Ecε

(1)

(2)

(3)

式中：

σ——混凝土的应力；

ε——混凝土的应变；

ft,r——混凝土单轴抗拉强度；

εt,r——ft,r对应的应变；

dt——单轴受拉损伤变量；

Ec——混凝土弹性模量；

at——混凝土受拉应力应变曲线软化段参数。

混凝土单轴受压应力应变曲线表达式如下：

σ=(1-dc)Ecε

(4)

(5)

(6)

式中：

fc,r——混凝土单轴抗压强度；

εc,r——fc,r对应的应变；

dc——单轴受压损伤变量；

ac——混凝土受压应力应变曲线软化段参数。

3 仿真结果分析

某水闸在校核工况下的静力仿真结果见图3，由图3可见，某水闸闸室结构各向位移均较小，其中受公路桥荷载及自重荷载作用，结构最大位移位于公路桥跨中位置，其竖直向位移为1.67 mm，小于规范允许扰度值l0/400的35 mm标准。

图3 某水闸静力仿真结果示意

闸室结构应力分析如下：受公路桥自重、公路桥荷载以及水荷载的影响，泉港闸交通桥大梁底部中间部位出现了1.32～1.45 MPa的拉应力，超过泉港闸C25混凝土抗拉强度(见表1)，因此，交通桥部位出现多处损伤，但最大损伤值仅为0.11，不会影响结构正常使用；受闸门自重、公路桥荷载以及水荷载的影响，泉港闸牛腿部位出现了0.88～1.12 MPa的拉应力，极小部分区域超过泉港闸C20混凝土抗拉强度(见表1)，因此，牛腿与闸门连接处出现局部细微损伤，损伤值仅为0.08，不会影响结构正常使用；其余各部位应力均为超过混凝土静态抗拉强度。

某水闸在不同放大系数地震动荷载作用下的损伤破坏情况如图4所示，由图4可见：地震动放大系数的提升对水闸损伤分布及破坏深度的影响十分可观。如图4a所示，在原始Koyna波地震荷载作用下，闸室结构大面积出现表层损伤，主要集中在启闭机房，交通桥和闸墩迎水面底部位置，其中闸墩部位出现损伤主要是由于未考虑地基的非线性特性，在线弹性材料与非线性材料的交界部位出现应力集中；交通桥部位的损伤主要集中在桥墩支座以及大梁底部，在规范荷载标准下已属于出现地震后的最不利情况；启闭机房部位的损伤主要集中于闸墩支座以及启闭机房侧面顶部，闸墩支座处损伤主要是由于启闭机房的侧向刚度远低于闸墩结构，因此，在震动发生时将出现变形不协调的情况导致该部位出现应力集中，而启闭机房侧面顶部处损伤主要是由于鞭梢效应，该部位出现的动力响应远大于底部闸墩处。如图4b所示，当地震动放大系数为2.5时，原损伤部位的损伤面积明显扩大，损伤程度进一步加深，同时胸墙与闸墩衔接处也出现局部损伤。如图4c所示，当地震动放大系数为2.8时，损伤面积及损伤程度进一步提升，可以初步判断顶部启闭机房无法有效运行，达到抗震能力临界值。

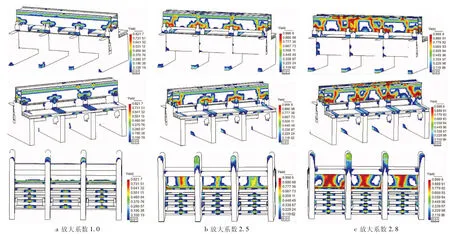
图4 不同加速度放大系数下某水闸结构损伤(D≥0.01)分布示意

为进一步验证某水闸的极限抗震能力，对结构在不同放大系数地震动荷载作用下时进入深度损伤的区域进行分析，结构深度破坏情况如图5所示。如图5a所示，在原始Koyna波地震荷载作用下，闸室结构进入深度损伤的区域有限，仅在交通桥大梁底部及启闭机房部位出现零星深度损伤，不会影响结构正常运行；如图5b所示，当地震动放大系数为2.5时，深度损伤部位的损伤面积明显扩大，变化主要出现在顶部启闭机房与闸墩衔接部位，此时机房易出现局部开裂现象，但结构整体仍能正常运行；如图5c所示，当地震动放大系数为2.8时，深度损伤面积进一步提升，顶部启闭机房出现损伤贯通区域从而整体失效，此时已无法有效控制闸门，可以判断工程无法正常运行，因此，认定2.8倍的Koyna波地震荷载即为某水闸的极限抗震能力。

图5 不同加速度放大系数下某水闸结构深度损伤(D≥0.6)分布示意

4 结语

本文通过仿真某水闸静动态荷载作用的下的结构响应，分析了其应力分布、结构变形及破坏情况，并在此基础上从损伤破坏的角度进一步分析了结构在不同放大系数地震动荷载作用下的工作性态。

研究表明地震动放大系数的提升对水闸损伤分布及破坏深度的影响巨大。对于某水闸结构而言，地震易损区域主要集中在启闭机房，交通桥和闸墩迎水面底部位置，均属于可预见的损伤部位，经计算最终认为某水闸结构的极限抗震能力为2.8倍的Koyna波地震荷载。地震荷载的随机性是其最为重要的特性之一，工程随时面临着超过抗震设计的荷载考验，因此研究抗震分析时，应充分了解结构的极限抗震能力，为结构安全运行提供保障。