基于不同植被指数的TRMM数据降尺度及误差校正研究
张寒博, 韦梦思, 覃金兰, 徐 勇, 窦世卿
(桂林理工大学 测绘地理信息学院, 广西 桂林 541006)
降水是维持全球水循环的一个重要环节[1-2],降雨量的大小、强度对农作物的科学种植起着不可忽视的作用[3]。现有研究表明TRMM数据可以为农业干旱监测[4]、草地监测等[5]提供科学的参考。华中地区河网密集,容易引发洪涝灾害,水土流失较为严重[6],华中地区是我国粮食主产区和重要的商品粮生产基地[7],通过研究华中地区降水的分布情况,可以为水土保持和农业发展等提供科学依据。
降水数据主要有3个来源:①传统气象站数据; ②地面气象雷达数据; ③热带测雨卫星(tropical rainfall measuring mission, TRMM)数据[8]。传统气象站数据质量受制于气象站点的数量,在一些站点数量较少且地表类型复杂的地区,数据准确度不能满足应用需求[9-10]。非降水回波对雷达降水估测影响较大,导致雷达降水数据误差大。TRMM数据覆盖范围广,可得到区域连续的降水数据,在一定程度上可以替代气象数据[11]。许多学者的研究证明TRMM数据在珠江流域[12]、湖南省长株潭地区[13]、金沙江流域[14]、怒江流域中上游等[15]国内地区均具有较好的适用性。现阶段,TRMM数据分辨率已不能满足应用需求,降尺度方法也层出不穷,李琼等[16]采用逐步回归、BP神经网络、GWR模型对TRMM数据进行降尺度,结果表明 GWR模型校正效果最优;熊俊楠等[17],基于GWR模型实现了青藏高原地区TRMM数据的降尺度;曾业隆等[18]基于地形起伏度,通过GWR模型提高了TRMM数据的空间精度。现有的研究主要采取单因子进行TRMM降尺度,且在华中地区尚缺乏相关研究。由于TRMM降尺度数据与真实数据存在一定的误差,许多学者致力于提升TRMM降尺度数据精度的研究[19-20]。现有多种校正方法,不同的校正方法在同一地区的校正精度有所差别,不同地区地形差异也决定了不同地区优选校正方法的差异,需要通过试验加以确定优选的校正方法。为此,本文基于GWR模型,以EVI和NDVI两种植被指数因子及地形因子为自变量,TRMM数据为因变量,对华中地区2001—2019年的TRMM数据进行空间降尺度。再对优选的降尺度数据进行GDA和GRA校正,最后通过气象站数据在不同时间尺度对校正前后的数据进行对比分析。
1 材料与方法
1.1 研究区概况
华中地区(图1)是中国7大地理分区之一,地处我国的中部(24°58′—36°22′N,108°21′—116°39′E)[21],由湖南、湖北、河南3省组成,总面积约为5.60×105km2,约占全国总面积的5.9%[22],是我国东西地势与南北气候的过渡地带。区域内地势西高东低,属温带季风气候和亚热带季风气候,雨热同季,受到全球气候变暖的影响,夏季可能会发生区域性极端日降水事件。

图1 华中地区气象站空间分布
1.2 数据源及预处理
本文采用2001—2019年的TRMM 3B43(version 7)月降水数据、MOD13A3数据均来源于NASA网站(https:∥search.earthdata.nasa.gov/)。其中TRMM数据空间分辨率为0.25°×0.25°(大约为27.5 km×27.5 km),经过投影变换、角度旋转、单位换算等预处理,并将一年12期的TRMM月数据进行求和,获得TRMM年累计数据;NDVI,EVI数据从MOD13A3数据中获取,其空间分辨率为1 km×1 km,进行波段提取、投影变换、最大值合成等处理,并对一年12期NDVI,EVI月数据求平均,分别得到年均NDVI、年均EVI数据。DEM数据从地理空间数据云(http:∥www.gscloud.cn/)中获取,空间分辨率为90 m×90 m,经过投影转换、重采样等处理,并利用ArcGIS获得坡度、坡向数据。气象站数据来源于中国气象局国家气象中心(http:∥cdc.cma.gov.cn/home.do),包括2001—2019年华中地区56个地面气象站降水数据以及研究区外一定范围的地面站点数据,经过数据整理,累加计算出年降水数据。
1.3 研究方法
1.3.1 GWR模型 GWR模型是Brunsdon等[23]提出的一种用于量化空间异质性的局部参数估计方法[24],是普通线性回归模型的扩展。GWR模型将数据的空间位置嵌入到回归参数中,引入地理距离权重进行最小二乘法逐点参数估计,来分析空间数据非平稳性的统计回归模型。其计算基本公式为:
(1)
式中:yi为第i个样本点因变量的降水量;xit为第t个自变量的第i个样本点的观测值; (ui,vi)表示第i个样本点的经纬度坐标;β0(ui,vi)为第i个样本点的常数项回归参数;βt(ui,vi)为第t个影响因子对第i个样本点的线性回归参数;ε(ui,vi)为模型在第i个样本点所计算出来的残差值;n为点的数量。
1.3.2 数据降尺度 由于降水量和地形、植被等因素存在空间非平稳性,所以可以对华中地区TRMM数据与同期的NDVI值、EVI值值、高程、坡度和坡向数据建立GWR模型,来实现TRMM数据的空间降尺度,其详细步骤为: ①将1 km×1 km分辨率的NDVI值、EVI值、高程、坡度、坡向数据重采样为与TRMM数据相同的空间分辨率0.25°×0.25°。 ②设低分辨率的TRMM数据(0.25°)为因变量,NDVI数据(0.25°)/EVI数据(0.25°)、DEM数据(0.25°)、坡度数据(0.25°)、坡向数据(0.25°)为自变量,设置核函数参数为ADAPTIVE,内核带宽参数为CV(选择这两个参数建立的GWR模型所得到的数据决定系数较高),建立低分辨率GWR模型。从回归模型中得到各自变量对应系数、常数项及残差项。 ③将各自变量系数、常数项和残差项利用反距离权重法插值得到高分辨率的自变量系数值、常数值和残差值(1 km)。 ④基于GWR模型,将高分辨的数据进行模型回代,得到空间分辨率为1 km的TRMM降尺度数据。
1.3.3 数据校正 尽管通过降尺度,很大程度上提高了TRMM数据分辨率,但与气象站数据相比仍存在很大的误差,因此有必要对降尺度数据进行校正。分别利用GRA,GDA对降尺度数据进行校正,从而获得更高精度的降水数据。GDA校正的大致过程为: ①将研究区56个气象站点随机分配成试验点(36个)和验证点(20个),计算试验点及其研究区周边气象站数据和对应位置降尺度TRMM数据降水量之差; ②选择反距离权重的插值方法,将差值的点数据转换为连续的面数据; ③将降尺度TRMM数据和插值的差值相加,得到校正后的降尺度TRMM数据。
GRA校正步骤和GDA校正相似,不同的是将试验点及其周边气象站数据和降尺度TRMM数据相比,并将相加改为相乘即可。
1.3.4 精度指标 本文以气象站数据作为“真实值”,用决定系数(R2)、相对误差(BIAS)、均方根误差(RMSE)对降尺度数据进行精度评定。R2评定降尺度降水数据与气象站数据的线性相关性,其值在0到1之间,值越大相关性越高;BIAS反映降尺度数据与气象站数据的偏离程度,BIAS越接近0数据越精确;RMSE来评定误差的整体水平。计算公式为:
(2)
(3)
(4)
2 结果与分析
2.1 TRMM数据适用性分析
通过2001—2019年研究区内56个气象站年尺度降水数据与相对应的TRMM数据构建线性回归函数。由图2可知,R2为0.630,BIAS为0.072,RMSE为250.09 mm,上述精度评价指标说明,TRMM年尺度数据与气象站年尺度数据具有较好的相关性。其中BIAS数值为正,表明TRMM年尺度数据存在一定程度的高估现象。通过计算每个气象站年尺度数据与相应位置TRMM年尺度数据的R,构建华中地区56个站点R的泰勒多边形(图3),可以看出R的范围为0.54~0.97,高于0.75的点比例为85%,且都通过了0.05的显著性检验。

图2 TRMM年尺度数据和实测年尺度数据的关系散点图

图3 基于气象站点的研究区R值空间分布
将华中地区2001—2019年TRMM月尺度数据和56个气象站月尺度数据按照季尺度分别进行合成,并对TRMM季尺度数据进行相关性分析。由图4可以看出,春季(R2=0.818)、夏季(R2=0.710)、秋季(R2=0.788)和冬季(R2=0.865)的TRMM季尺度数据与气象站季尺度数据存在较好的相关性。且与TRMM年尺度数据的相关性比较,TRMM季尺度数据优于TRMM年尺度数据。BIAS数值波动范围为0.052~0.069,4个季节相对误差相差不大。RMSE值最大的季节是夏季(RMSE=55.72 mm),最小的为冬季(RMSE=14.08 mm)。与TRMM年尺度数据的均方根误差(RMSE=250.09 mm)相比,TRMM季尺度数据的精度明显优于TRMM年尺度数据。

图4 TRMM季尺度数据与实测季尺度数据散点图
对华中地区56个气象站数据和TRMM数据在月尺度上进行相关性分析,构建月尺度数据的线性回归方程。从表1可以看出,月的R2在0.637~0.875浮动,其中R2最小的月份是8月,最大的月份为12月,普遍来说,降雨量较少的月份R2较大。各个月的BIAS数据表明,BIAS数值范围为0.030 1~0.983 0,其中最低的月份为7月。RMSE的数值在12.115~62.414 mm,数值最大的月份为7月。月尺度数据与季尺度数据在R2、BIAS和RMSE具有一致性。
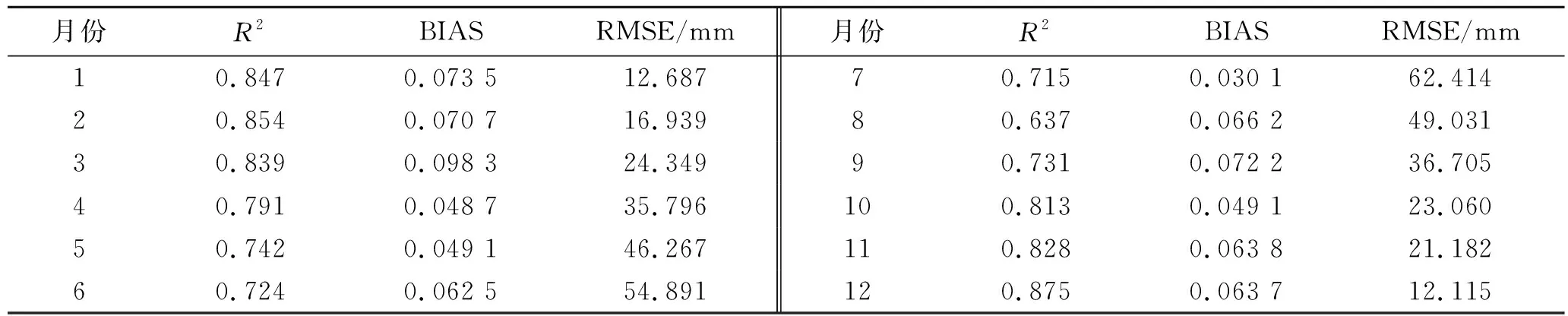
表1 研究区TRMM月尺度数据适用性的验证结果
2.2 TRMM降尺度及校正数据分析
2.2.1 年TRMM降尺度数据校正分析 本文将DEM数据、坡向数据和坡度数据分别结合EVI数据和NDVI数据对TRMM数据降尺度,得到1 km的TRMMYear-EVI数据和TRMMYear-NDVI数据。由图5可知,降尺度前后数据空间分布具有一致性,具体表现为降水量由南到北、自东向西递减趋势,符合地理学上的地带性差异。华中地区的降雨主要集中在湖南地区,东南边缘地带相较其他地区降雨量较多。在华中地区的中部,降雨量分布呈现一条明显的过渡带,往北递减,往南递增。降尺度后的数据均能更为详细的反映华中地区降水量的空间分布,在河南东南部、湖北东部、湖南南部等地区尤为明显,且TRMMYear-EVI数据比TRMMYear-NDVI数据更接近TRMM数据。
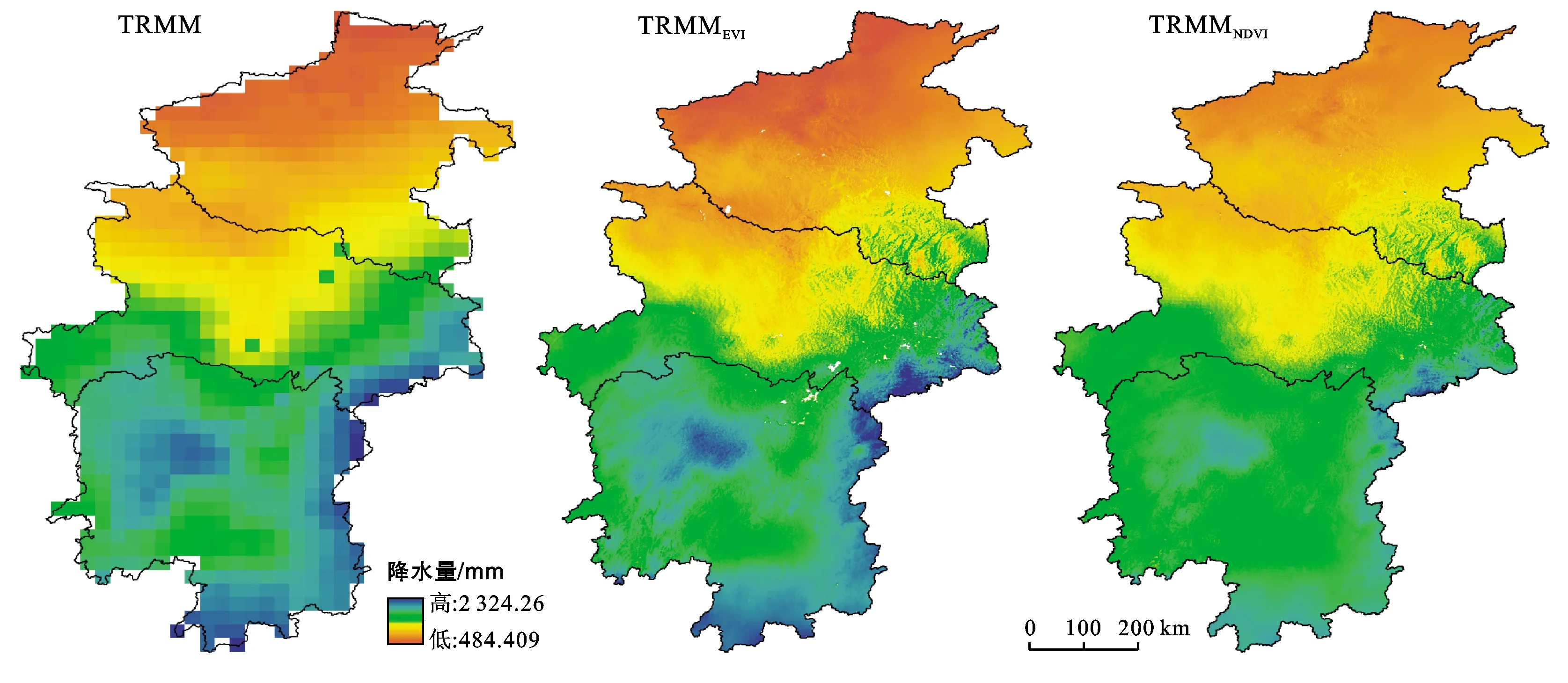
图5 研究区年平均TRMM数据降尺度结果
为了进一步对比两种植被指数反演TRMM数据降尺度的效果,分别对两种降尺度数据和气象站数据进行相关性分析。由图6可知,TRMMYear-EVI数据(R2=0.847,BIAS=-0.044,RMSE=173.55 mm)比TRMMYear-NDVI数据(R2=0.836,BIAS=-0.040,RMSE=176.31 mm)精度更高,表明在华中地区EVI与TRMM数据相关性更强。

图6 研究区降尺度数据和实测数据的相关性分析散点图


图7 研究区多年平均TRMM数据降尺度校正结果


图8 研究区季尺度数据降尺度校正结果


表3 研究区季数据验证结果


图9 研究区多年平均月降水量

图10 研究区月尺度数据精度指标变化
3 讨论与结论
3.1 讨 论
杜方洲等[26]对东北地区TRMM数据进行深入研究,部分东北地区的冬季降水以降雪形式为主,1月数据拟合效果较差;夏季气候多变,7月数据的模型拟合效果也不理想。东北地区比华中地区的地理纬度高、降雪量多,且东北地区有较大面积的东北平原,夏季短冬季长;而华中地区夏季降雨量大且易发生极端日降雨[25],地形以山地和丘陵为主。在气候与地形等因子的影响下,东北地区与华中地区TRMM的冬季数据质量呈现相反的结果,夏季数据质量呈现一致性。日后可以深入研究TRMM数据与各种因子间具体的相关性,探究华中地区TRMM数据季节性周期规律。
目前,基于两种植被指数因子反演TRMM降尺度对比研究较少,现有熊俊楠等[17]采用EVI、杜方洲等[26]和金辉明等[27]采用NDVI为因子进行TRMM数据降尺度研究,张寒博等[28]研究表明在长江流域NDVI比EVI降尺度效果更好。本文研究结果表明在华中地区TRMMYear-EVI数据比TRMMYear-NDVI数据精度更高。从EVI和NDVI的原理公式出发,可知EVI相较NDVI考虑到了蓝光波段、气溶胶和冠层的影响。NDVI在植被覆盖率高的地区,红光波段容易出现饱和现象,而EVI综合了大气抵抗植被指数和抗土壤植被指数的特性。综上所述,由于不同的植被覆盖情况和不同植被指数公式的特性,在不同地区采取EVI或NDVI对TRMM数据降尺度,得到的效果呈现差异性。
通过GDA校正和GRA校正,可以进一步提升TRMM降尺度数据的精度。国外学者Zhang[20]对位于中国西南地区的红河流域TRMM降尺度数据进行校正,研究表明在该地区GRA校正效果优于GDA校正效果。而本文研究的华中地区TRMM数据的降尺度校正效果与之相反。红河流域于华中地区相比,纬度较低,北回归线横穿流域,日照时间较长。由此,经纬度位置差异可能影响GDA校正和GRA的校正效果。另外从GRA的原理公式出发,可知,当TRMM数据或气象站数据部分缺失而呈现异常高的数值时,TRMM数据与气象站数据相差过大,GRA比值倍数增加,导致使用GRA校正出来的降尺度数据较大程度上偏离真实地表降雨情况。GDA校正使气象站数据与TRMM数据进行差值运算,虽然不可避免出现误差,但在华中地区所呈现的效果表明GDA校正效果更佳。综上,GDA校正和GRA校正的效果差异可能与地理纬度和数据质量有关。
3.2 结 论
(1) 年、季和月尺度的TRMM数据在华中地区都体现出较好的适用性。与气象站数据的R2,BIAS和RMSE均满足精度要求。
(2) 通过GWR模型实现了TRMM数据空间分辨率由0.25°到1 km的提升,对降尺度数据和气象站点插值数据进行分析,两者具有一致的空间分布。

(4) 对季、月的TRMM降尺度数据进行GDA校正,结果显示降雨量大小与校正效果呈现正相关。但在校正前后,冬季数据具有更高的可信度。

