新能源场站并网测试系统数据分段技术研究
安瑞峰 , 李晓军 , 常 潇
(1.山西世纪中试电力科学技术有限公司, 山西 太原 030001;2.国网山西省电力公司电力科学研究院, 山西 太原 030001)
0 引言
近年来,山西新能源发展迅猛,截至2020 年6月新能源装机已突破2 500 万kW,预计2025 年底全省新能源装机容量将超过6 000 万kW。 新能源场站接入电力系统后,按相关标准[1-7]要求在6 个月内向电力系统调度机构提供有关运行特性的测试报告,测试内容包括有功/无功控制能力测试、电能质量测试等。目前,测试工作主要有现场测试、数据分析、报告编制等环节,测试工作存在任务繁重、数据分析效率低等问题。 针对这些问题,文献[8—11]提出了新能源场站并网测试装置的标准及研制,但在数据处理方面依然存在效率较低、工作量较大的缺点。 基于此,本文设计了一套新能源场站并网测试系统, 并针对手动功率区间划分效率较低的问题,提出了一种基于奇异值分解SVD(singular value decomposition)的数据自动分段算法,实现各测试区间的数据自动分段,提高了测试效率。
1 源荷储一体化并网自动测试方法
1.1 测试系统布置
本文设计的新能源场站并网测试系统由待测设备模块、数据采集模块和数据分析模块3 部分组成。其中,被测对象是指所需要测试的风电场、光伏电站,测试项目包括有功/无功控制能力测试、电能质量测试等;数据采集模块主要实现各测试项目的功率及电能质量数据采集, 即采集风电场的有功、无功、电压、电流等基础数据和谐波、不平衡度等电能质量数据;数据分析模块是实现数据自动分段与分析、测试报告自动生成的核心模块,执行数据导入、基于奇异值分解的数据自动分段、数据处理、生成测试报告等程序。
1.2 测试装置要求
电能质量分析仪与功率分析仪应当满足国标对于测试设备的要求,能有效准确采集各项测试数据。测试项目持续时间长,测试数据量大,数据采集装置应配置与服务器实时通信的能力,宜采用数据采集卡。装置的数据传输通信支持IEC 61850 国际规约,便于扩展。
1.3 测试流程
自动测试整体流程有6 部分。 一是测试信号(即测试数据):包括被测对象的有功功率、无功功率、相电压和线电压值、功率因素、谐波电压和谐波电流、三相不平衡度、频率、长时闪变和短时闪变值。 二是选择测试方法:国家标准规定了不同测试项目的测试时间、测试要求。 测试方法应基于国家标准,在现场可根据测试精度、测试时间和测试项目等,合理选择测试方法。 三是测试数据处理分析:采集电能质量分析仪和功率分析仪的测试数据,存入数据库,并传入数据分析模块,进行数据分析。 四是数据分析模块:判断是否需要分析不同功率区间的测试结果,若需要则运用数据分段算法对数据进行分段。 五是分段后的数据传入数据处理系统,计算出测试项目所需要的指标与结果。 六是生成测试报告:数据处理算法基于国家标准,对传入的数据进行处理,计算出结果并输入报告生成模块,匹配报告模板,自动生成测试报告。
2 基于SVD 的数据自动分段技术
2.1 数据自动分段流程
根据测试要求,多项测试项目需要在电站不同功率区间下进行测试,获得数据。 识别不同功率区间是测试数据分析的核心工作,其首要任务就是检测过渡段。定义过渡段为从一个平稳数据段到另一个平稳数据段的变化区段。本文以某风电场有功功率测试为例,有功功率从80%功率区间以10%为步长下降,一直到20%功率区间,其中有6 个过渡段。检测过渡段,需要检测到快速变化段的起始和结束时间,从而明确各功率区间的时间边界。基于此,不同功率区间数据的自动分段问题也可以被认为是一个检测数据边界的问题。而功率数据与其他测试数据有着时间以及采样点上的对应关系,所以找到了各功率区间数据的边界,按照时间和采样点的对应关系就能对数据进行分段。过渡段数据的变化规律呈现出快速变化的特点, 而SVD 对于数据不连续的奇异点有着良好的检测性能,故本文采用奇异值分解进行数据自动分段,步骤如下。
步骤1:数据预处理。 读取功率测试数据,记为P,P 由 N 个采样点构成,可以表示为 P=[P1,P2,…,PN]。进行差分处理并构造其Hankel 矩阵,如式(1)所示。

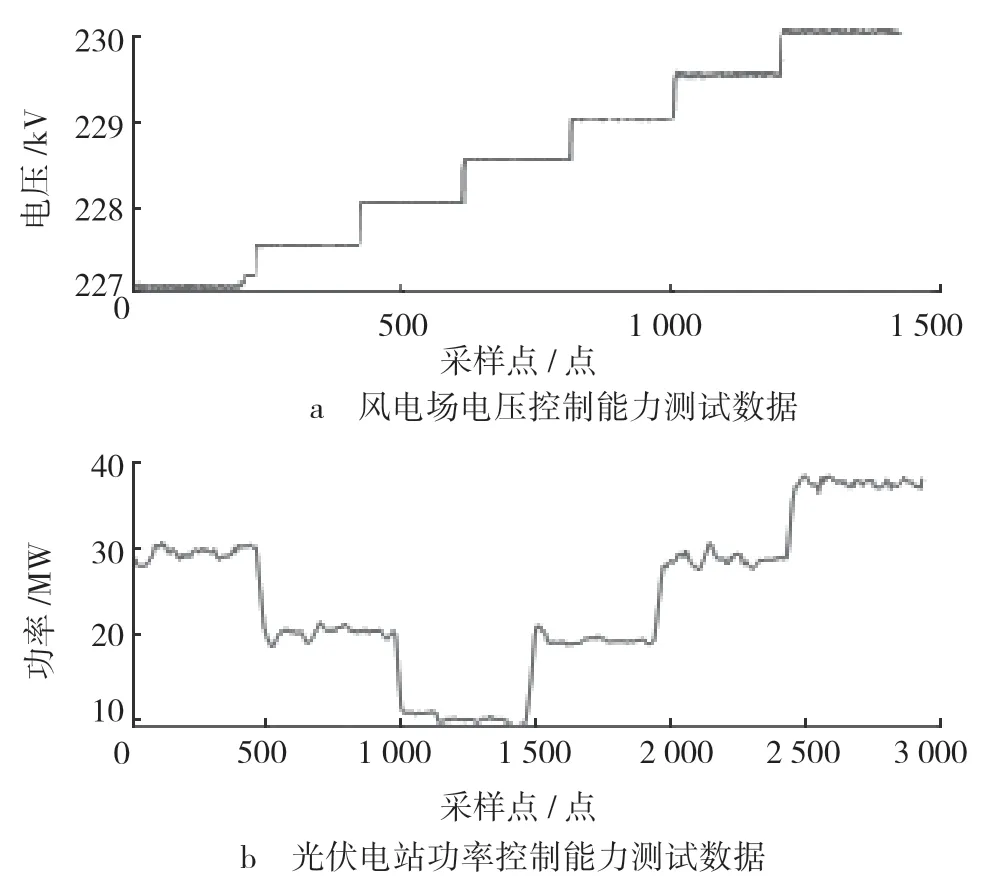
其中,n 满足 1 步骤2:奇异值分解。 对矩阵X进行奇异值分解得到式(3)的结果,提取其奇异值λi。当数据处于突变位置时,其奇异值表现为剧烈突变,所以,SVD可以计算出数据突变点的边界。 步骤3: 构建自适应阈值进行数据自动分段。由于各电站在容量上表现出高度的不确定性,若采用固定阈值会造成该阈值无法适用于所有数据分段流程。而自适应阈值是解决固定阈值造成分段准确度较低缺陷的有效办法。 步骤4:数据分段修正。 本文以多个采样点为计算窗口逐点计算该段数据的SVD 值。 由于SVD计算得到的过渡段结束时刻存在一定延时,故需要对其进行修正。 奇异值分解的基本概念为:对于一个任意的实矩阵 X(其中 X=∈Rm×n),必然会存在两个正交矩阵U 和 V,U 和 V 可表示为 此时,式(2)被称为矩阵的奇异值分解,其中S满足以下条件 S 称为奇异值对角矩阵,其中式(4)中O 为零矩阵,并且满足λ1≥λ2≥λ3≥…≥λa≥0,λi(i=1,2,…,a)被称为矩阵 X 的奇异值,其中 a=min(m,n)。式(2)可进一步被表示为 本文中数据分段问题可等价为过渡段边界计算问题, 其过渡段边界计算方法如2.1 节所述,其中阈值的设置尤为重要。 为了检测算法的准确性,引入“漏警率”和“虚警率”来验证算法。 其中,PL表示漏警率;PX表示虚警率;DW表示未被检测到的过渡段事件个数;DD表示多被检测到的过渡段事件个数;DA表示实际过渡段个数。 由于不同测试项目的测试数据不同,所以固定阈值会造成某些项目的测试数据无法准确进行数据分段,分段结果的漏警率和虚警率都会偏高。 为了解决固定阈值造成数据分段准确度低的问题,本文提出自适应阈值的方法。而确定自适应阈值的前提是找到过渡段幅值特征与计算出的奇异值的关系。本文基于30 组仿真数据,计算过渡段幅值与最大奇异值的关系,计算结果显示,过渡段幅值和最大奇异值是线性关系,因此可以用最大奇异值作为阈值。 根据曲线拟合角度以及仿真测试,本文选取最大奇异值的0.65 倍作为自适应阈值。 对数据逐点构造其Hankel 矩阵后进行奇异值分解, 可得到奇异值随时间变化的曲线。 基于2.3节所提的自适应阈值,如果奇异值大于自适应阈值到奇异值小于自适应阈值,则这一段数据可以认为是过渡段。而奇异值分解的输入信号长度与过渡段边界计算结果相关,如果输入信号长度过长,则无法准确计算出过渡段边界, 如果输入信号长度太短,则会大大增加计算时间。 基于仿真数据和实测数据验证,本文采取输入信号长度为9,在这个取值下算法具有最佳表现。 本文以9 为计算窗口逐点计算SVD 值,由于计算得到的过渡段边界具有一定的时间延时, 所以需要对其进行修正。 本文以奇异值最大值的10%作为阈值向前搜索100 个点,得到修正后的过渡段边界。 本文基于MATLAB 平台,生成1 000 条仿真数据,验证算法对过渡段的计算性能,以漏警率和虚警率来进行量化。 数据生成规则如下。 a) 数据一共有3 种关键参数,即过渡段数量、过渡段幅值以及稳定段的采样点数。 本文针对这3种关键参数,每种参数生成10 条数据,3 种参数组合一共有1 000 条仿真数据。 b) 过渡段数量从 3 到 30, 以 3 为步长增加;过渡段幅值从1 到10,以1 为步长增加;稳定段的采样点数从100 到1 000,以100 为步长增加。 c) 每一条数据加上噪声,噪声为随机生成,范围为0 到过渡段幅值的0.1~0.5 倍。 得到的仿真数据以上述数据分段方法进行过渡段数量以及过渡段边界的检测,检测到的过渡段边界与真实的过渡段边界相差稳定段采样点数的5%即记为错误,以字母G 表示过渡段幅值,得到的仿真结果如表1 所示。 表1 仿真数据验证结果 % 从表1 可以看出,本文提出的数据分段的准确率较高, 在加入0.1 倍和0.2 倍过渡段幅值的噪声情况下均能准确进行数据分段, 在0.25 倍过渡段幅值噪声的加入下,分段准确率稍低,并出现了虚警和漏警的情况, 但0.25 倍过渡段幅值的噪声在实际工业中已远远超出了标准。 选取新能源场站实际测试的2 条数据进行仿真验证,实测数据如图1 所示。 从实测数据分析结果来看, 本文所提方法能够准确识别过渡段边界,从而对数据进行分段。 图1 实测数据示意图 本文针对新能源场站测试工作中手动数据分析效率较低的问题,提出了一种新能源场站并网测试系统,基于奇异值分解对数据进行自动分段,通过仿真及实验验证,得到如下结论。 a)设计了一套新能源场站并网测试系统,基于数据采集装置与数据分析模块,实现数据的自动处理与分析计算,并自动生成测试报告,极大地提高了测试效率。 b)提出了基于奇异值分解的测试数据自动分段方法,能准确识别数据过渡段边界,从而对数据进行分段,提高了测试效率,减少了人工操作。 c)对所提方法进行仿真和实测数据验证,数据分段效果较好,在实际测试分析工作中有广阔的应用前景。2.2 奇异值分解


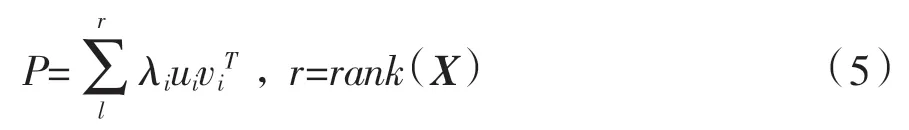
2.3 构建自适应阈值

2.4 过渡段修正
3 算例验证
3.1 仿真数据验证

3.2 实测数据验证
4 结论

