数学实践与建模对就业选择问题的分析

公 丽

（华北水利水电大学，河南 郑州 450046）

1 问题重述

随着就业形势的日益严峻，越来越多的求职者面临就业时选择困难的问题，如何权衡兴趣专长、工资待遇、发展前途、工作环境等问题成为很多人的困扰，本文通过利用层次分析法建立数学模型，对如何在就业问题上做出科学的选择进行了分析。而层次分析法可以对就业的选择提供一定的依据。层次分析法简称AHP,是将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础上进行定性和定量分析的决策方法，适合于目标值受很多因素影响的，难以定量描述的决策问题[1]。

对于此问题，首先建立层次结构，将决策问题分为总目标、各层目标、评价准则，然后构造各层次所有判断矩阵、单排序及一致性检验，最后通过进行层次总排序得到最低层中各方案对目标排序的权重，此最终权重最大者即为最优的方案，从而将难以直接量化的难题变得更加直观。

最后对建立的模型进行了评价，提出了该模型的改进方法。

2 模型假设

（1）假设求职者的能力都符合公司招聘的要求；

（2）假设求职者的性别、年龄以及婚姻状况对于决策没有影响；

（3）假设有C1、C2、C3 三个公司可以供求职者选择；

（4）假设B1、B2、B3、B4、B5、B6 分别代表专长发挥、工资待遇、发展前途、单位声誉、工作环境、生活环境六个影响因素，且就业者在就业时只考虑这六种因素；

（5）假设A 代表求职者的就业满意度。

3 模型的建立与求解

3.1 构建层次结构

将此决策的目标值、需要考虑的因素以及决策对象按思维过程分为最高层、中间层，绘出层次结构图，如图1 所示。

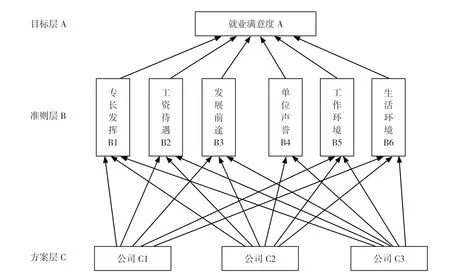
图1

3.2 构造成对比较矩阵

不把所有的因素放在一起进行比较，而是两两进行比较，以减少不同性质的因素相互比较的困难，来提高比较结果的准确性。

根据比较规则和综合意见，准则层B 和目标层A 的比较判断矩阵如图2 所示。

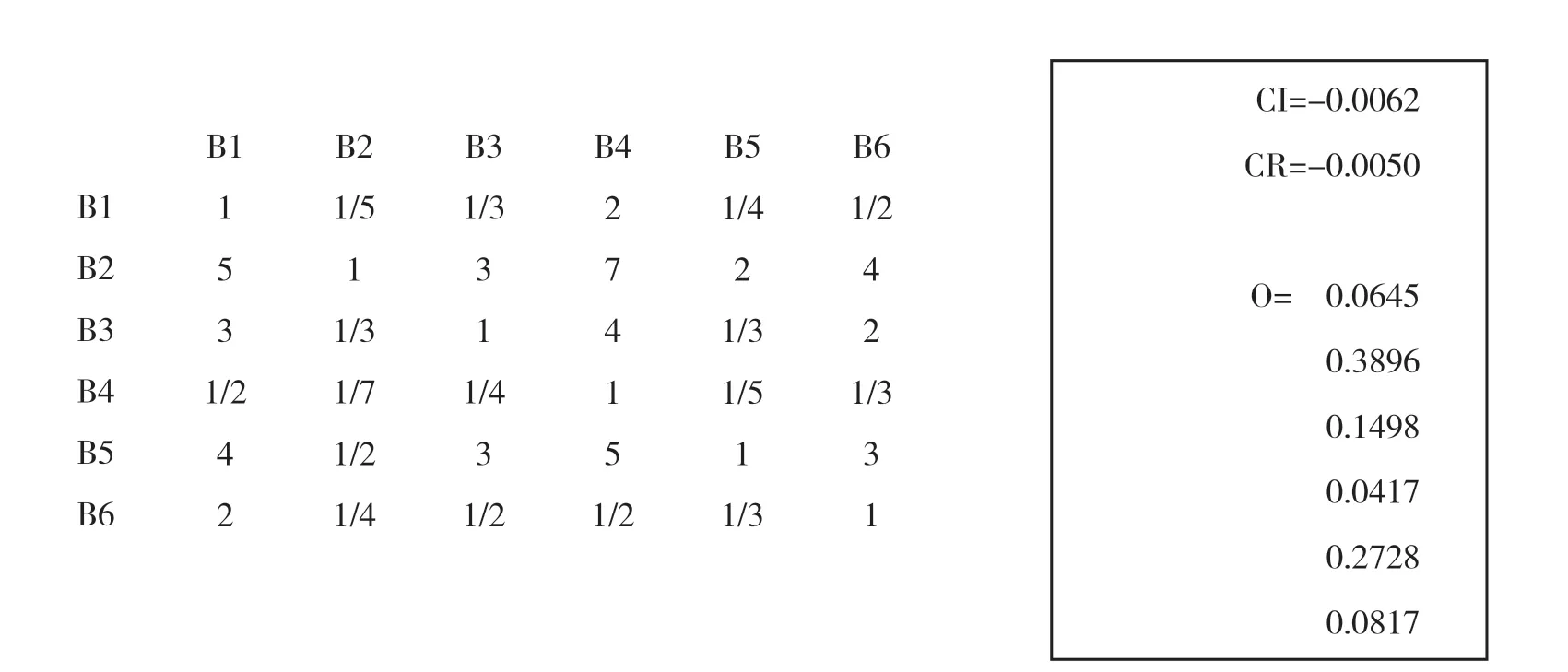
图2

3.3 方案层C 对准则层B 的比较判断矩阵

如上图3～8 所示。

图3

图4

图5

图6

图7

图8

3.4 层次总排序

通过MATLAB 软件的计算，判断矩阵均通过一致性检验，因此进行总排序即可得到最低层对于目标的排序权重。

由上表1 可以看出，三个待选公司的排序为：公司C3（0.4585）、公司C1（0.3407）、公司C2（0.2009）。

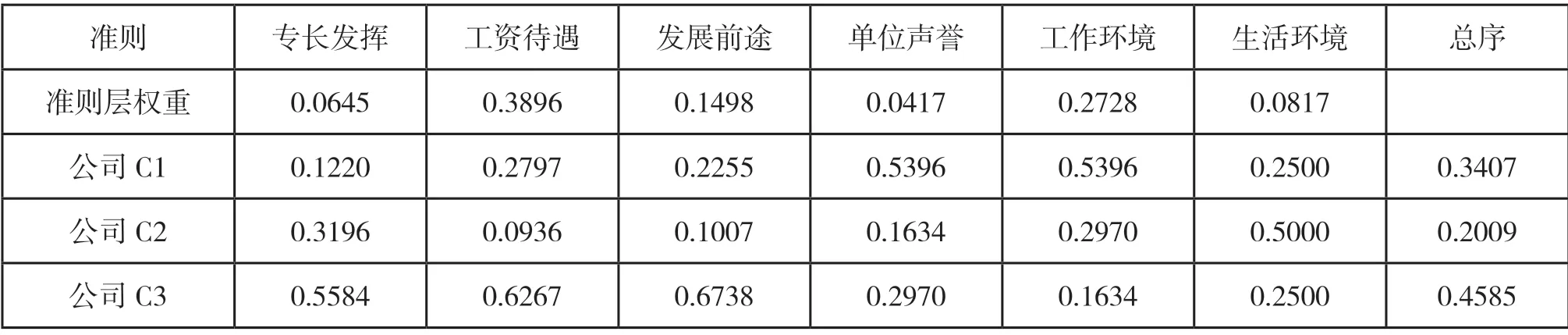
表1

4 结论与分析

近年来我国的就业形势十分严峻，求职的竞争压力的增加使他们在就业的时候不得不对一些条件做出舍取，面对能否在就业时找到适合自己发挥专长的岗位，工作单位的福利待遇如何，自己或者单位未来的发展状况如何，单位在社会的影响力怎样，工作条件，城市位置如何等问题都是影响求职者选择的因素。很多时候，对于不同的人来说这些因素的重要性是不同的，而且这些影响因素很难直接量化，众多因素相互交错影响又给人们的判断提高了难度，如何在就业时综合考虑以上影响因素的影响从而做出科学的决策是我们面临的一个问题。

本文运用层次分析法将难以直接量化的问题通过科学的计算得出相对可靠的量化结果，同时该方法不单纯追求高深的数学知识，而是把定性方法与定量方法有机的结合起来，使复杂的系统分解为一层又一层，在这个过程中，使人们的思维变得更加系统化，更加数学化，而且在计算过程中，运用MATLAB 编程使复杂的计算过程变得简洁、准确、高效。在计算过程中对判断矩阵进行了一致性检验，保证了误差在可控制的范围内。

在改进方面，该模型没有考虑到求职者性别、年龄对决策的影响。其次，层次分析法本身也具有以下不足：（1）判断矩阵中的各个标度的赋值有很大的随意性，同时，这种赋值方式对于单人决策是可行的，对于多人决策，可能会出现冲突。（2）判断矩阵的赋值方式有待斟酌，即矩阵中对称位置权数取倒数关系。（3）正反矩阵的这种“倒数”赋值会在后面的计算标准权重和相对权重中产生“意见放大”现象。因此，我们应当有一种方法，一方面清楚明了地用来确定多人决策过程中对相关要素的赋权问题；另一方面解决“意见放大”问题。对此，我们可以借鉴穆迪优先图表法来解决[2]。