纳米颗粒添加对熔融盐传热特性的影响

刘 吉， 胡槐生 ，杨双维， 王少君， 李丽君

(1.中国能源建设集团安徽省电力设计院有限公司， 安徽 合肥 230601;2.华北电力大学 生物质发电成套设备国家工程实验室， 北京 102206;3.大唐陕西发电有限公司灞桥热电厂， 陕西 西安 710065)

1 背景介绍

目前能源日益紧缺同时大规模使用化石能源造成了环境污染，因此太阳能作为一种分布广泛且清洁的能源得到了越来越多的应用[1]。太阳能发电具有来源广，运行费用低，不污染环境等特点，主要发电方式包括光伏发电和光热发电[2]。其中太阳能光热发电是将太阳光通过反射镜汇集到太阳能收集装置上，加热装置内的传热介质，然后带动发电机发电的发电方式[3]。这种方式产生的电是交流电，因此，太阳能光热发电系统与储能系统结合后具有电负荷可控能力，能够用于调峰，利于电网稳定，除此之外，还能克服太阳能分布分散性、稀疏性等缺点[4]。

光热发电的储能系统储能材料对储热系统的效率和成本有重要的影响[5]，因此储热介质材料的选择便显得十分重要。目前常用的储热介质有水、熔融盐、导热油、相变金属、高温混凝土等[6]。相比于其他储热材料，高温熔融盐有潜热大、热稳定性好、储能密度高、价格低廉等优势，被越来越多的研究者认可重视，未来有很大发展潜力。为了进一步提高光热电站中熔盐的传热能力以减少发电系统建设成本，现在许多改性方法已经应用于光热熔盐，目前发展比较成熟的改性方法主要有复合熔融盐[7,8]、熔盐添加多孔超导材料[9-12]、熔盐基纳米流体[13]。前人提出了不同的添加纳米颗粒熔融盐形成纳米流体强化传热的机制，现阶段被承认的潜在机制主要有以下三种：布朗运动理论[14]、半固体层理论、团聚理论[15]。

为了提高光热发电系统中蓄热系统的传热特性，开发一种热导率更高的储热材料，本研究通过计算径向分布函数(Radial Distribution Function,RDF)及均方位移(Mean Square Displacement,MSD)对Hitec盐及Hitec盐基纳米流体的热导率进行分子动力学模拟，从微观角度分析不同温度、不同质量分数/颗粒粒径对热导率的影响，揭示传热的微观机理，为熔盐纳米流体的性能调控提供技术思路。

2 研究方法

本研究基于分子动力学模拟原理，采用Buckingham势函数与平衡态分子动力学等方法模拟分子动力学过程，同时通过计算MSD、扩散系数以及RDF，揭示熔盐基纳米流体传热机理。

2.1 分子动力学模拟原理及技术参数

分子动力学(Molecular Dynamics，MD)模拟是一种基于经典的牛顿力学来模拟微观尺度体系分子运动的方法，其计算的步骤是先从分子体系的不同状态构成的系统中抽取样本，然后对体系的构型进行积分计算，最后以构型为基础进一步计算体系的热力学性质及其他宏观物理量[16]。

分子动力学技术参数主要包含边界条件、模拟系综、模拟时间步长、模拟系统弛豫。边界条件是指在求解区域边界上所求解的变量或其导数随时间和地点的变化规律，在MD模拟中，因为模拟的微观尺寸很小，以及方法的限制，通常都选用周期性边界条件。模拟系综就是指在某些限定条件下，使得整个区域内的大量原子的某些性质整体保持一致的不同系统的集合，常用的系综有：正则系综(NVT系综)、等温等压系综(NPT系综)等，根据不同的模拟要求，选择合适的模拟系综[17]。模拟时间步长是系统对热力系统状态的采样间隔时间，理论上取样的间隔时间越短，也就是系统状态的取样频率越高，所得到的数据就越精确，但计算机的计算负担也相应越大，计算过程所用的时间也越长。因此，对于一个热力过程，选取一个合适的时间步长是很关键的，一般情况下，时间步长选取0.000 5 ps就足够对系统完整取样，且不会浪费计算资源。弛豫就是使系统达到稳定的动态过程，一般情况下，在对系统建模过后，模型的参数与预期系统需要的初始参数相差较多，如果直接进行采样，则会造成模拟值浮动较大，甚至模型崩溃的后果。因此，在对系统进行正式的热力学参数取样前，需要使系统达到预期的初始参数值，这就需要系统在相应的系综下弛豫一段时间，来使系统内部参数达到要求。

2.2 分子动力学模拟过程

在确定体系的分子模型、力场模型、初始条件后，设定模拟的技术参数，进行正式的模拟。在模拟开始之前需要将模拟需要的各种参数按照MD模拟程序要求的格式写入不同的文件，以便于MD模拟程序进行读取。接下来就是要确定MD程序为所输出的参数信息、输出信息的频率以及包含这些参数信息的文件格式等。随着模拟的进行，用于记录模拟体系内各原子速度和位置的相文件(Trajectory File)或历史文件(History File)就会迅速的积累，生成数量庞大的数据。在实际的模拟过程中，由于相轨迹文件的增长速度很快，很容易写满整个储存空间，因此有必要预先估计相轨迹文件的大小，给定一个适宜的输出间隔步数。最后，再对所得到的系统内的原子信息进行后期处理，得到体系的热导率和比热容等热力学参数。整个的MD模拟流程如图1所示。

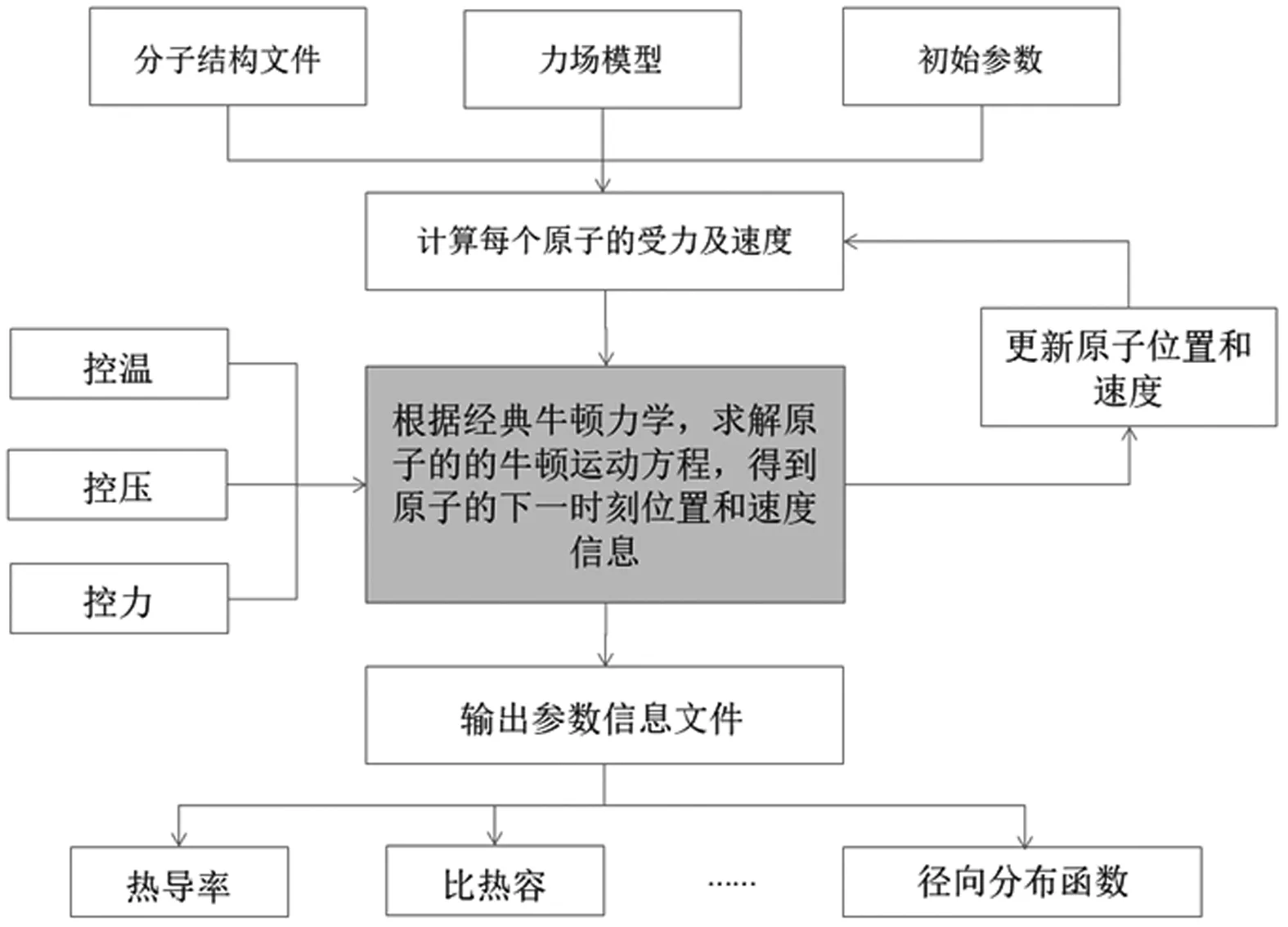
图1 分子动力模拟流程图

2.3 势能函数

当进行模拟时，可以用分子间的相互作用势函数来代表分子之间的相互作用力。一般两体势函常用L-J势函数[18]、Morse势函数[19]等。但L-J势函数的排斥项可能会与实际情况偏离较远，故Buckingham[20]提出了具有指数函数形式的排斥项，即：

(1)

相应的相互作用力函数为：

(2)

计算原子交叉相互作用的混合规则为：

(3)

(4)

(5)

为了调整排斥力的硬度，可以从Buckingham的指数项系数着手。Buckingham势多用于熔融盐热力学性质的研究[21]。

2.4 平衡态分子动力学方法

平衡态分子动力学(Equilibrium Molecular Dynamic, EMD)方法是通过使整个热力学系统处于动态平衡，根据线性响应理论中的Green-Kubo公式以及能量流自相关函数来求得热导率。在Green-Kubo公式中，给出了热导率与微观热流之间的关系。

(6)

式中：V—热力学体系的体积；kB—玻尔兹曼(Boltzmann)常数；T—模拟体系的温度(K)；J—微观热流。

(7)

式中：ri(t)—表示原子i在不同时间下的空间坐标；ei(t)—表示原子i在不同时间下的能量大小。

2.5 均方根位移和扩散系数

均方根位移MSD表征了粒子的随机运动的程度，计算式如下。

x2=2DS(t)

(8)

(9)

式中：η—基液的粘度；d—颗粒直径；kB—玻尔兹曼常数(kB=1.380 649×10-23J/K)。

2.6 径向分布函数

径向分布gAB(r)为在以A类原子为中心的空间球体积内发现B类原子的概率，与B类原子在整个空间内的分布的概率之比。利用几何关系可以计算球壳的体积。

(10)

若整个模拟体系的体积为V，体系中含有A类原子nA个，含有B类原子nB个，当A、B两种原子在整个体系内的分布是均匀时，在球壳体积内发现A、B两类原子的概率分别为4πρAr2δr和4πρBr2δr，其中ρA、ρB是A、B原子的原子数密度。

径向分布函数gAB(r)可以表征模拟体系的内部结构，尤其是A、B两类原子之间的相互距离关系。例如，gAB(r)峰值所对应的半径即为A、B两类原子之间的最可几距离，峰的高度和尖锐程度表征了两类原子之间的结构有序度。通过径向分布函数还可以计算出两种原子之间的配位数NAB：

(11)

其中，积分的上限为径向分布函数的第一个极小值点对应的位置。通过配位数可以清楚地解两类原子之间的相互作用的强弱。

3 结果与分析

3.1 模型重构

根据ICSD数据库，利用Materials Studio进行建模，构建了如图1中所示的二氧化硅(SiO2)晶胞，该晶胞由四个硅原子和八个氧原子组成。利用此晶胞构建相应直径的球形SiO2纳米颗粒，而后在SiO2纳米颗粒表面构建Connolly表面，以防止盐粒子进入纳米颗粒内部。为避免尺寸效应对模拟结果的影响[22]，正方向Hitec盐(质量分数比为NaNO3∶KNO3∶NaNO2=7∶53∶40)盒子边长设置为5 nm。SiO2纳米颗粒质量分数为2%、4%、6%的纳米流体模型如图2(a)～(c)所示。

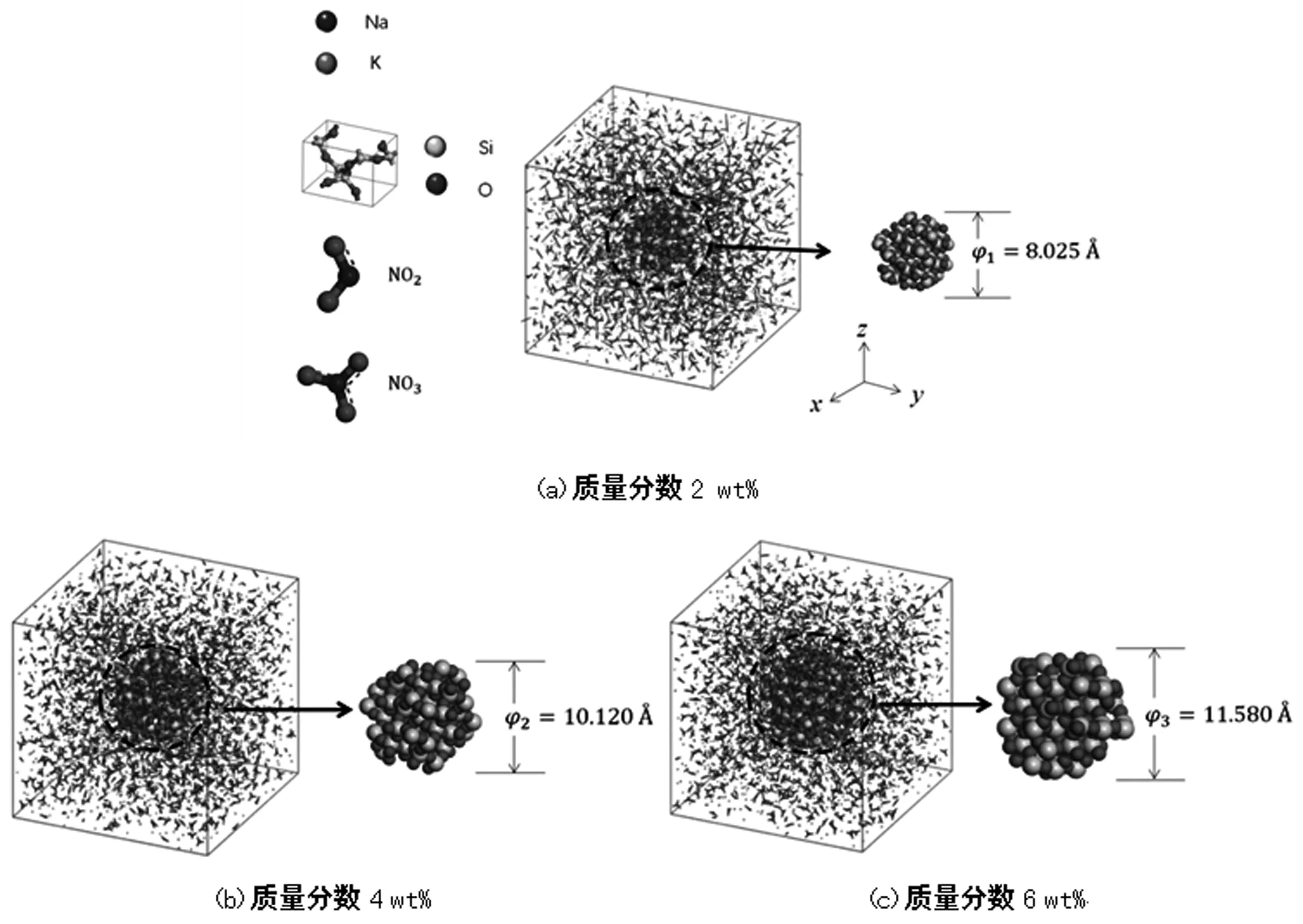
图2 Hitec盐内添加SiO2纳米颗粒模型图

3.2 力场

采用Buckingham势来描述体系分子之间的作用力，熔融盐基纳米流体内部粒子之间的作用参数如表1和表2所示[23]，SiO2纳米颗粒与盐之间的作用力通过式(3)～(5)计算，其中，亚硝酸根中的氮元素和氧元素分别表示为N2和O2，硝酸根中的氮元素和氧元素分别表示为N3和O3。

表1 分子间势函数参数

表2 分子内势函数参数

3.3 平衡分子动力学方法计算热导率

本研究运用EMD方法计算了Hitec盐基纳米流体的热导率。模拟中，时间步长设置为0.5 fs。三个方向均施加周期性边界条件。分别选取Hitec盐工作温度内473.15 K、573.15 K、673.15 K、773.15 K四个温度进行模拟。在给定体系温度后，对结构进行能量最小化处理。接下来使系统先分别在NPT系综、NVT系综下驰豫100 ns，而后在NVE系综下驰豫200 ns。图3表示573.15 K，添加4 wt%纳米颗粒工况下NVE系综体系的热流自相关函数、温度和能量随时间的变化。从图3(a)可见热流自相关函数HCACF随时间收敛至0；图3(b)、(c)中系统的温度和能量都已稳定收敛。其他工况也如此，此处不再赘述。

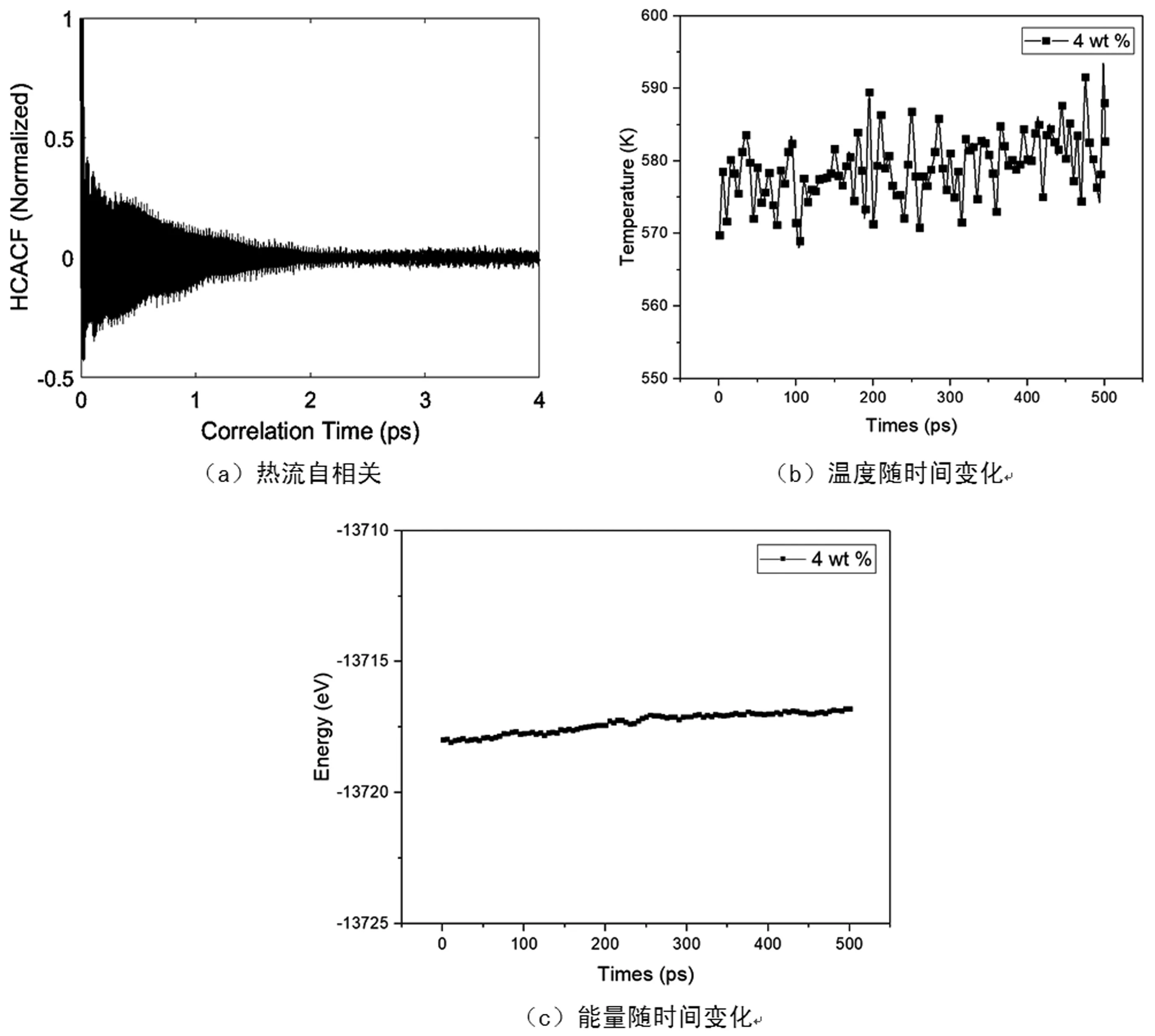
图3 HCACF、温度及能量变化图

3.4 纳米颗粒添加对Hitec盐热导率的影响

3.4.1 温度的影响

图3为纯熔盐与熔盐基纳米流体热导率随温度的变化关系。可见，573 K温度下，纯熔盐的热导率为0.503 W/(m·K)，该数值与文献[24]的实验测量值误差小于5%，由此证明本研究的模拟是可靠的。从图中还可以看出，不同温度下，熔盐基纳米流体的热导率始终都是大于纯熔盐，该结果表明熔融盐中添加纳米颗粒对熔盐的热导率有一定的提升作用，从而使得熔融盐在实际的应用中的吸热和释热时间缩短。在太阳能热发电系统中，越高的传热性能可使水更快地转化为水蒸汽，从而提高发电效率。此外，图4表明，熔盐及其纳米流体的热导率均随着温度的升高而降低。该变化趋势与文献[18]的结论一致。

图4 热导率随温度变化关系曲线

3.4.2 质量分数/粒径的影响

图5为573.15 K温度下熔融盐基纳米流体的热导率随质量分数/粒径改变的变化图像。从图5中可以看出，当质量分数小于4 wt%时，纳米流体的热导率随纳米颗粒质量分数/粒径的增大而升高；然而，当质量分数大于4 wt%时，热导率呈下降趋势。Li等人[22]研究发现，当纳米颗粒的直径一定时，纳米颗粒的质量分数越大，熔盐的热导率越大。桑等人[25]研究发现，当质量分数一定时，纳米颗粒的直径越大，熔融盐基纳米流体的热导率越小。也就是说，颗粒质量分数与纳米流体热导率是呈正相关关系，而颗粒粒径与热导率呈负相关关系。因此，质量分数与粒子直径之间存在一个竞争机制。低质量分数时，颗粒质量分数的影响占主导；而高质量分数时，颗粒粒径作用更为显著。因此，随着质量分数增加，纳米流体热导率出现先增加后降低的趋势。

图5 热导率随质量分数/粒径的变化关系曲线

3.5 均方根位移和扩散系数

为了揭示纳米颗粒对熔盐热导率提升的机理，本研究计算了MSD和扩散系数。本文分别计算了不同温度下纯Hitec盐与添加SiO2的熔盐中基液粒子的MSD，如图6所示，其斜率就是扩散系数DS。在四个温度下，都能够看出，当添加了SiO2后，基液粒子的MSD都会减小，其中减小比例最大的为温度是773 K的情况，减小比例最大的为温度是473 K的情况。在温度为473 K时，加入SiO2后，MSD从120下降到110左右，尽管随着时间延长，无论是否加入SiO2都会发生MSD增大的现象但能够看出，未加入SiO2的基液粒子其MSD增长速度(扩散系数)较快，加入SiO2的基液粒子MSD增长速度(扩散系数)较慢，最后两者MSD相差比例更大。温度为573 K、673 K和773 K的情况和温度为473 K的情况大同小异，都展现出相同的趋势。有研究者提出[26]，加入纳米颗粒后体系也增加了额外的热量输运，进而引起基液微对流。所以可以根据基液微对流的强弱程度，判断颗粒加入后体系额外的热量输运程度，进而判断纳米颗粒对纳米流体热导率的影响。从图6中可以看出，随着温度升高，纳米流体基液与纯熔盐粒子的MSD增大，说明温度升高体系的总能量也升高，基液粒子无规则运动加快。此外，在同一个温度下，加入纳米颗粒后的基液的MSD均小于纯Hitec盐的MSD。图7给出了纳米流体基液的扩散系数与纯熔盐的扩散系数之比(DS/DP)。图中结果显示，在研究的温度范围内，DS/DP均小于1，这说明纳米颗粒的添加不但不会增加额外的热量输运，还会阻碍热量输运。因此，基液微对流不是熔盐纳米流体热导率升高的原因。

图6 不同纳米颗粒质量分数下的MSD

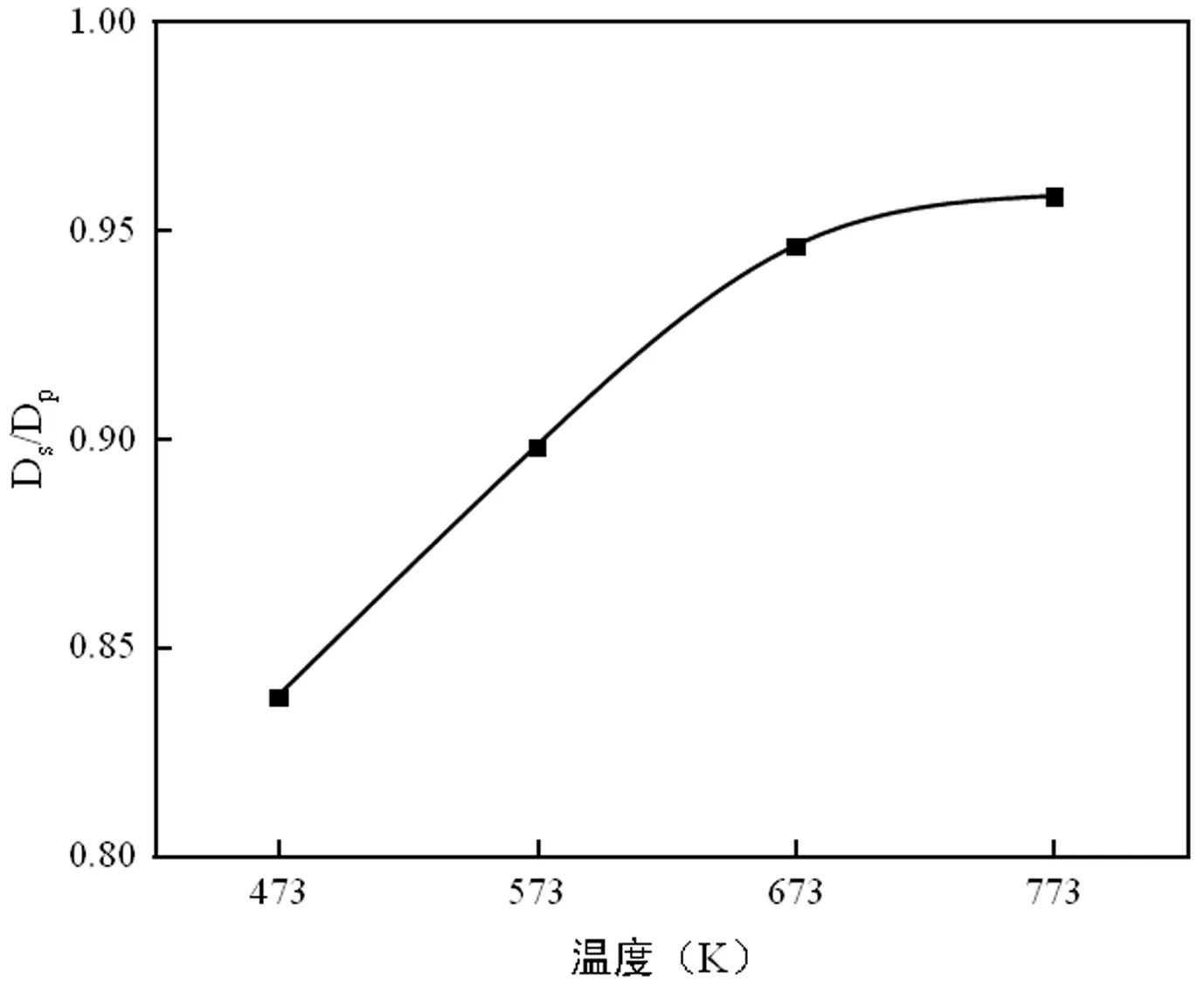
图7 纳米流体基液的扩散系数与纯熔盐的扩散之比

3.6 径向分布函数

进一步通过计算径向分布函数(RDF)分析熔盐纳米流体的微观结构。图8至图14给出了基液中不同离子间的RDF。

从图8、图11及图14中可以看出，当质量分数为4 wt%时，Na-Na与Na-K离子对的RDF第一峰的高度最高，其余两种情况的峰高与峰宽基本相同，而K-K离子对之间的RDF质量分数为6%时最高，其余两种情况下都基本一致，第一峰所在位置几乎相同。由此可知，添加纳米颗粒对阳离子之间的相对位置没有影响。

图8 Na-Na离子之间的RDF

从图9、图10、图12及图13中可看出，三种质量分数例下的RDF第一峰的位置有所不同，说明添加纳米颗粒会影响基液中阴阳离子之间的作用力。其中，质量分数为4 wt%和6 wt%时的K-N2、K-N3离子对的RDF峰所在位置几乎一致，都小于2 wt%的情况。由此说明2 wt%的结构的钾与氮之间的结构比较松散，其余两种情况的结构较致密。Na-N2在三种质量分数下的RDF几乎相同，说明添加纳米颗粒对其作用力无影响，而尤为重要的是Na-N3之间的RDF第一峰的位置从左至右为4 wt%、2 wt%、6 wt%，与热导率的模拟结果变化趋势相同，说明Na-N3之间的配位数对热导率的变化起到主要决定作用。随着温度的升高，熔盐基体的RDF会减小，结构变得疏松，从而导致整体的热导率减小[18]。

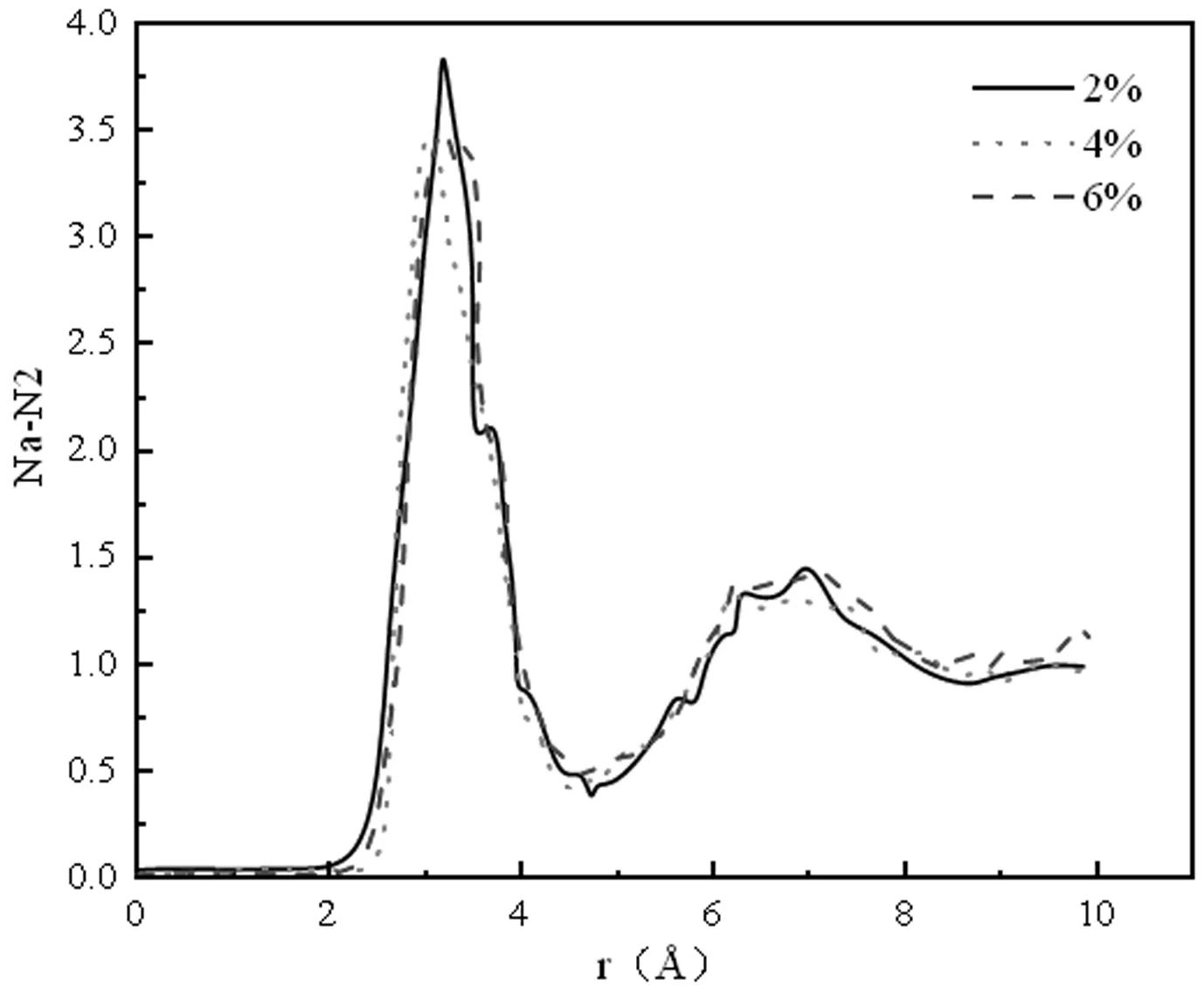
图9 Na-N2离子之间的RDF

图10 Na-N3离子之间的RDF

图11 K-K离子之间的RDF

图12 K-N2离子之间的RDF

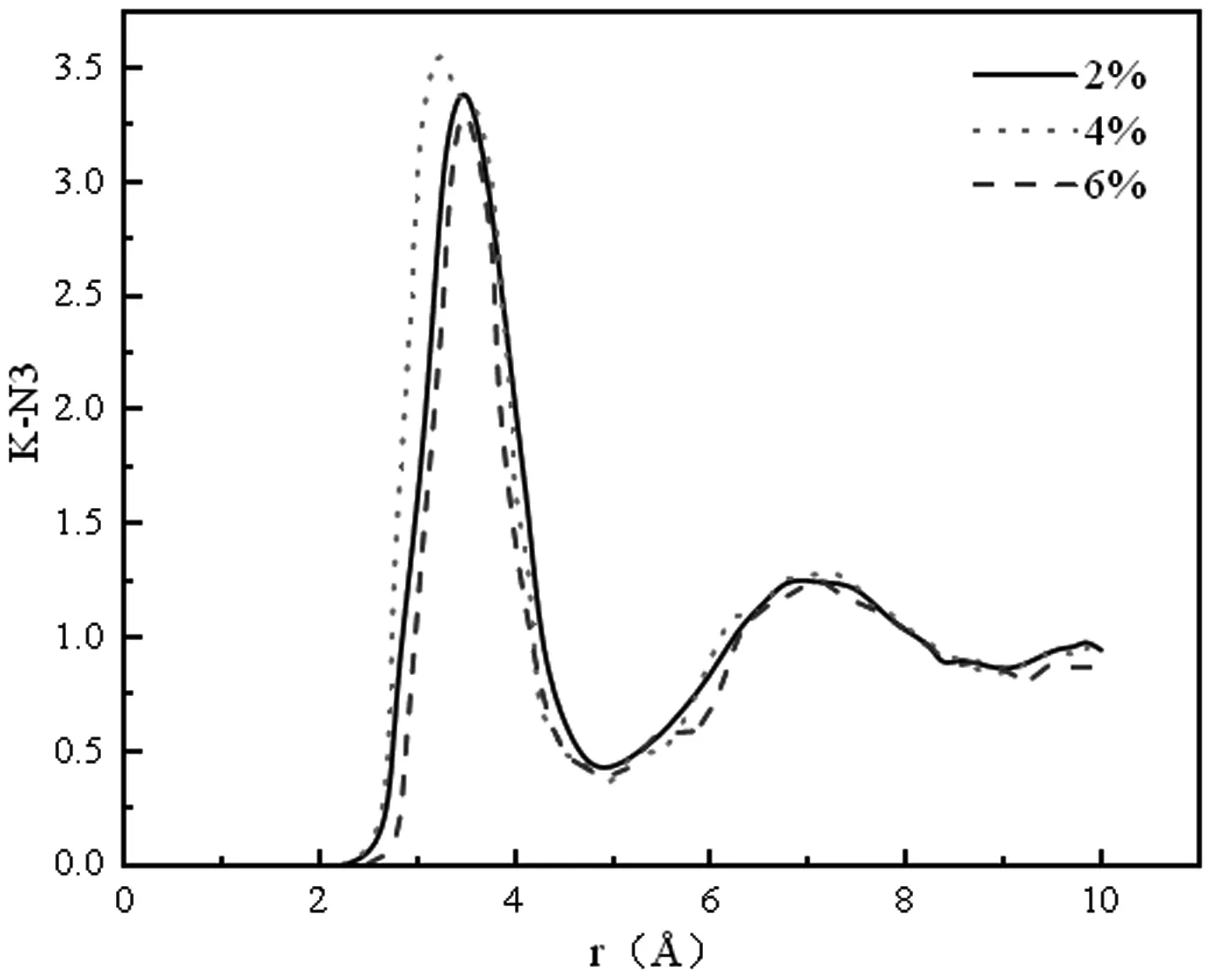
图13 K-N2离子之间的RDF

图14 K-Na离子之间的RDF

4 结论

本研究首先通过Materials Studio软件建立了添加不同直径、不同质量分数纳米颗粒的纳米流体，以及纯Hitec盐模型。之后，对模拟中所应用的力场势函数模型参数及合理性进行了详细描述。并且详细介绍了EMD方法计算热导率过程中的模拟细节及参数设定，展示了热导率的模拟结果，并与前人的模拟结果进行对比，验证了结果的正确性。利用对纳米流体基液及纯Hitec盐的MSD及RDF的结果分析了热导率的变化机理。得到以下结论：

(1)熔融盐中添加纳米颗粒会使热导率增大，熔融盐与熔融盐纳米流体的热导率都随着温度的升高而降低。

(2)纳米流体的热导率与添加颗粒的质量分数成正比，与颗粒直径成反比。

(3)通过对均方根位移和扩散系数的计算可知，纳米颗粒的添加不但不会增加体系额外的热量输运，还会阻碍热量输运。

(4)通过对径向分布函数的计算可知，Na-N3之间的配位数对热导率的变化起到主要决定作用。随着温度的升高，熔盐基体的RDF会减小，结构变得疏松，从而导致整体的热导率减小。