基于粒子群优化极限学习机的睡眠分期方法

吴振华，邱 倩

（南昌航空大学 软件学院，江西 南昌 330100）

0 引 言

睡眠是人类最重要的生理活动之一，良好的睡眠有利于人类保持身体健康。但随着时代的进步，人们在工作、学习、生活上的压力也随之增加，越来越多的人患有睡眠障碍。睡眠障碍会产生许多问题，包括疲劳、焦虑、抑郁和死亡风险等，是具有公共危害性的疾病[1-2]。

多导睡眠图（Polysomnography, PSG）常用于睡眠状态评估，它利用脑电图机将被测试者整夜的脑电（Electroencephalogram, EEG）、肌电（Electromyogram, EMG）、心电（Electrocardiogram, ECG）、眼电（Electrooculogram,EOG）、呼吸等生理参数同步记录，由专业的医生根据R&K准则[3]，将睡眠状态划分成清醒期（WAKE）、快速眼动期（Rapid Eye Movements, REM）和非快速眼动期（Non Rapid Eye Movements, NREM）。其中NREM又可以划分为N1～N4共4个子阶段，其中N1、N2期称为浅度睡眠，N3、N4期称为深度睡眠。虽然PSG测试结果较为准确，但需要在专业的睡眠中心进行数据采集，不适用于民众长期日常监护。且在数据采集记录后，专家会手动识别每个数据所生产的睡眠阶段，这项工作繁琐且劳累，因此，设计一种高准确率的自动睡眠分期方法已成为睡眠医学领域的研究热点[4]。

ECG信号和呼吸信号作为人体重要的生理信号，在一定程度上能够反应测试者在夜间的睡眠情况，国内外均有学者利用ECG信号对睡眠进行分期检测，并取得了不错的成就。Mourad Adnane[5]等通过心率变异性（HRV）、去趋势波动分析（DFA）和窗口去趋势波动分析（WDFA）方法从RR序列中提取7个特征，采用支持向量机（Support Vector Machine, SVM）的方法对SLEEP-WAKE二类分期进行分类，得到78.5%的准确率。王金海等[6]采用SVM设计并实现了基于心率变异性的睡眠分期算法，采用主成分分析（PCA）的方式降低了数据间的冗余度，获得了较高的预测精度。冯晓星[7]等通过提取单通道ECG信号的RRI和HRV六个衍生特征，利用隐马尔可夫（Hidden Markov Model, HMM）模型对特征进行训练，睡眠分期准确率达92.3%。

一些学者尝试将ECG信号和呼吸信号相结合进行睡眠建模。M.O.Mendez[8]等基于时域自回归模型对特征进行提取并使用HMM对心率变异性进行分析，监测准确率为72%。许良[9]将HMM和BP神经网络（Back Propagation Neural Networks, BPNN）相结合的混合算法应用到睡眠分期计算中，先利用HMM对心率呼吸率信号进行建模，得到各睡眠状态下的HMM模型，然后利用BPNN对HMM分期计算的结果进行记忆训练，提高睡眠分期的识别率。李涛[10]等在通过引入ECG信号QRSTP波之间的间距、幅值以及RR间期的分位数等新的时域特征后，利用最小二乘支持向量机（LSSVM）方式对所提取的特征进行建模分类，在六类分期上得到75.5%的准确率。由此可见，利用人工智能方式建立睡眠模型具有一定的可行性。

BPNN非常适用于睡眠阶段的分析，它容错性强，具有学习复杂非线性关系的能力，但是它反向学习过程缓慢，可能导致局部最优解出现[11]。极限学习机（Extreme Learning Machine, ELM）克服了BPNN的缺点，它基于神经网络的概念，精确度高、处理数据时间短，相较于BPNN具有更好的泛化能力和处理速度。在建立睡眠模型后，提取原始数据中的特征数据进行学习，但并非所有特征都是有效的，并且ELM初始化参数生成方式的随机性会导致模型不可避免的产生隐含层神经元冗余、对位置输入参数识别能力差等问题，从而降低预测精度。针对这些问题，本文通过粒子群优化算法（Particle Swarm Optimization, PSO）对原始特征数据进行择优选择以及对ELM的输入权值和隐含神经元的阈值进行寻优，从而建立PSO-ELM模型以提高睡眠模型的精度。

1 方 法

1.1 数据集

实验数据来自麻省理工学院提供的MIT-BIH多导睡眠数据库[12]，该数据库中共记录了17个受试者的相关数据，对于每位受试者，该数据库提供了包括EEG、ECG、呼吸和血压等4种生理数据，并提供了人工标注的睡眠分期标签，数据采样频率为250 Hz。睡眠分期遵循R&K准则，对每位受试者的生理数据按照30 s进行分段，并对睡眠阶段进行标注。

1.2 数据预处理

生理信号通常会受一些未知频率成分的干扰，因此本文对ECG信号和呼吸信号作滤波处理。一般ECG信号的频率范围为0.05～100 Hz，采用巴特沃斯低通滤波器对ECG信号进行预处理。呼吸信号的波形简单且频率较低，噪声主要以高频噪声为主。正常人的呼吸频率为0.2～0.4 Hz，采用Kasier低通滤波器对呼吸信号进行预处理，将滤波器的带通频率设为0.5 Hz，带阻频率设为1.0 Hz，带通波动与带阻衰减分别设为0.01和0.001。截取测试对象slp01a的一段数据（5 000个数据），滤波后的效果如图1所示。

图1 ECG信号、呼吸信号滤波处理

1.3 特征提取

1.3.1 HRV特征提取

HRV是指连续心搏瞬间心率的微小差异或逐次心跳间隔即RR间期的变化规律。主要受心脏交感和副交感神经双重调节和相互制约的影响，HRV还呈现出与脑电类相似的周期性变化规律，其时域、频域和非线性信号在不同的睡眠阶段具有不同的特点。本文选取的HRV特征见表1所列。

由表1可知，HRV的时域特征由mRR、SDNN、RMSSD、SDSD、NN50和pNN50构成。其中，mRR指相邻RR间期的平均值，SDNN指RR间期的标准差，RMSSD指RR间隔之间差异平方均值的平方根，SDSD指相邻RR间隔之间的差异标准偏差，NN50指相邻RR间隔相差超过50 ms的个数，pNN50指相邻RR间隔相差50 ms的个数占总间隔个数的百分比。

表1 HRV特征提取总结表

HRV的频域特征由VLF、LF、HF、TP、pLF、pHF和LFHF构成。一般HRV频谱划分为4个频带[13]：甚低频ULF（＜0.03 Hz）、极低频（0.03～0.04 Hz）、低频（0.04～0.15 Hz）和高频（0.15～0.4 Hz）。频域分析方法应选取一段信号进行频谱分析，睡眠分期标签的时间是30 s，因此本研究选取30 s的HRV信号作为时间尺度，提取该尺度内的频域特征。

近似熵（Approximate Entropy, ApEn）和样本熵（Sample Entropy, SamEn）是两种较为常用的非线性分析指标。此前，ApEn和SamEn更多用于分析脑电信号。将ApEn和SamEn应用于睡眠心率数据和呼吸数据的分析，可以定量描述在不同睡眠阶段下心率和呼吸的波动情况。本文采用ApEn分析HRV的非线性特征。

1.3.2 呼吸信号特征提取

呼吸作为人体重要的生理信号之一，随着睡眠的加深，测试者的呼吸频率也会逐渐降低。呼吸波有着类似HRV的变化规律，其时域和频域特征在不同的睡眠阶段有着不同的表现。本文选取的呼吸特征见表2所列。

表2 呼吸特征提取总结表

采用和HRV相似的时域分析方法，其中Resppeak_num指一段时间内呼吸波峰数量，Average_Resp指一段时间内呼吸波峰波谷的间隔平均值，Resppeak_valley_SD指连续波峰波谷的间隔标准差，Resppeak_SD指连续呼吸波峰的间隔标准差。

参考已有研究，将呼吸波频谱分为3个频带：极低频VLF（0.01～0.05 Hz）、低频LF（0.05～0.15 Hz）和高频HF（0.15～0.5 Hz）。呼吸波的频域特征在一定程度上反应了呼吸量的强弱，当呼吸频谱能量较大时，说明呼吸信号能量集中，呼吸活动比较有规律；当频谱能量较小时，说明呼吸信号能量分散，呼吸活动表现为随机性强、规律性弱。同时，本文也计算了呼吸波的近似熵来反应呼吸波的非线性特征。

1.3.3 心肺耦合信号特征提取

哈佛医学院的C.K Peng等人[14]将心肺耦合现象用于研究睡眠质量和睡眠呼吸事件。通过计算心率信号和呼吸信号在给定频率下的功率乘积，即测量互功率谱可以得到这两个信号在该频率下是否有较大的振幅。另外，计算心率信号和呼吸信号的相干性，由此可知这两个信号的振荡同步情况，即是否保持恒定的相位同步。用相干性和互功率谱相乘得到的结果来定量估计心肺耦合的强度。利用文献[15]中的研究方法，得到低频LF（0.04～0.10 Hz）和高频HF（0.10～0.40 Hz）频段范围内的耦合能量。

1.4 建模方法

1.4.1 极限学习机

极限学习机（ELM）[16]是一种有效的单隐含层前馈神经网络学习算法，它与传统的单隐含层前馈神经网络相比，能够有效克服传统神经网络因采用梯度下降法进行训练而导致陷入局部极值的缺点，并且具有处理速度快、泛化能力强、易于实现等优点，其结构示意如图2所示。

图2 ELM结构示意图

假设给定N个训练样本{xi, ti），1≤i≤N，xi=[xi1, xi2, ...,xim]T∈Rm，ti=[ti1, ti2, ..., tin]T∈Rn，则ELM的训练模型表示为：

式中：ωi表示连接网络输入层节点与第i个隐含节点的输入权值向量；βi表示连接第i个隐含层节点与网络输出层节点的输出权值向量；oj表示网络输出值。

为了取得较好的预测精度，训练过程应以零误差逼近训练样本，即：

联合式（1）和式（2）可得：

式（3）可表示为：

式中：Y为网络输出矩阵；H为隐含层输出矩阵。

由于H矩阵为常数矩阵，则ELM的学习过程可等价于式（4）中β的最小二乘解β′的求解过程，即：

式中，H+是矩阵H的Moore-Penrose广义逆矩阵。

1.4.2 粒子群优化算法

在粒子群优化算法（PSO）中[17]，所有粒子的适应值由适应度函数决定，每个粒子都被赋予速度用来搜索方向和距离，并且能够保存寻找的最佳位置信息。粒子群在初始状态下，通过计算个体的适应值选择个体的局部最优位置向量pbest和种群的全局最优位置向量gbest。在迭代寻优的过程中，通过pbest和gbest不断更新自身的速度和位置，即：

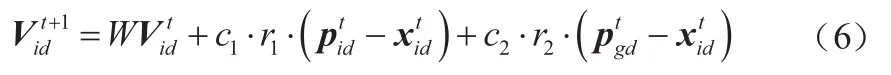
式中：W称为惯性因子，通过调整W的大小，可以对全局寻优性能和局部寻优性能进行调整；c1和c2称为加速常数，前者为每个粒子的个体学习因子，后者为每个粒子的社会学习因子，当c1和c2为常数时可以得到较好的解，一般取c1=c2∈[0，4]，通常设置c2=c2=2；r1和r2是0到1的随机因子，可增加搜索随机性。

1.4.3 粒子群优化极限学习机

处理好数据的所有特征后，需要选择出最具有代表性的特征放入极限学习机中。通过人工方式选择特征不一定能够得到最好的预测结果，并且ELM初始化参数生成方式是随机确定的，有可能导致隐含层神经元冗余、对未知输入参数识别能力差等问题，从而影响模型精度。面对上述问题，R. Ahila[18]等提出了PSO优化ELM的方法，该方法通过利用PSO算法对电力质量的数据特征以及ELM的输入权值和隐含神经元的阈值进行寻优，从而提高电力系统干扰分类模型的泛化能力和精确度。虽然睡眠状态分期与电力系统干扰分类属于不同的应用领域，但本质相同，都是对采集的信号进行特征提取，并通过提取的特征进行状态分类。因此，本研究利用R. Ahila等提出的方法建立基于粒子群优化极限学习机的睡眠分期模型（PSO-ELM）。

PSO-ELM模型中的每个粒子都用二进制表示，包含2个部分：特征掩码和隐含神经元。PSO-ELM 粒子表示见表3所列。

表3 PSO-ELM 粒子表示

特征掩码部分表示所选的特征，n表示所有特征的总数。当pf为“1”时，表示当前特征已被选中，如果为“0”则表示未选中该特征。隐含神经元部分表示PSO-ELM模型中隐含神经元的数量，其中N表示最大隐含神经元的总数。

在适应度函数中，利用ELM和总特征选择的精度对PSO-ELM模型进行评价，如式（7）所示：

式中：wA和wF是权重因子，表示分类精度acci和所选特征数的权重；nf是特征的总数；fj是特征掩码的第j位；acc表示分类精度，如式（8），其中分类正确和分类错误的例子分别用cc和uc表示。

PSO-ELM模型的详细步骤如下：

（2）对粒子pi在种群中的每个位置训练一个ELM分类器，并计算适应度函数 fi tnessi；

（4）设置迭代次数，并开始迭代；

（6）对粒子pi训练一个ELM分类器并计算适应度函数fi tnessi；

（7）如果粒子当前位置的适应度函数 fi tnessi为最大值，则更新局部最优解和全局最优解；

（8）如果迭代次数达到最大，则回到步骤（5），否则进行步骤（9）；

（10）利用训练好的ELM分类器对睡眠数据进行睡眠分期。

PSO-ELM模型的算法流程如图3所示。

图3 PSO-ELM模型的算法流程

2 实验与讨论

为证明利用PSO算法对数据特征进行寻优以及对ELM分类器中隐含神经元数量进行寻优后，能够有效提升睡眠分期模型的精度，本文以三类睡眠分期数据为基础做了以下实验：

（1）确定ELM分类器隐含神经元数量范围；

（2）ELM、SVM、BPNN分类器在原始特征空间中分类的精度评估与对比；

（3）PSO算法对ELM、SVM分类器在数据特征寻优后睡眠分类精度的评估与对比；

（4）PSO算法对特征以及ELM分类器中隐含神经元数量进行寻优后睡眠分类精度的评估；

（5）本文方法与现有睡眠分类方案的对比。

2.1 主成分分析

原始特征数据相对较大，数据与数据间存在一定的相关性，直接用这些特征指标来区分不同的睡眠状态会导致数据间的冗余，导致程序运行时间过长并对预测结果造成一定影响。因此，本文利用PCA对原始特征数据进行主成分提取，将原来具有一定相关性的数据重新组合成一组新的互不相关的综合特征向量，用更少的数据代替原先数据，提高运算效率。

对样本特征数据进行PCA处理并提取新的特征向量，如图4所示。由图中数据可知，当新的特征向量个数为16时，累积贡献率已达到95%，表明选取前16个特征向量足够表征原始数据。通过PCA对原始特征数据进行预处理，在满足原始数据不失真的条件下，降低了数据量和数据间的相关性，提高了算法的执行速度以及准确性。

图4 PCA特征降维

2.2 ELM隐含神经元数量

ELM分类器对原始数据的分类精度会随着隐含神经元数量的变化而变化[19]。为说明这种行为，以三类睡眠分期数据为基础进行实验。将ELM隐含神经元的数量从10个增加至110个，其中每新增10个为一次实验，计算在不同数量的隐含神经元下ELM分类器对三类睡眠分期的平均分类精度。表4为训练和测试时的精度变化，图5为相应精度变化图。根据表4和图5可以清楚看出，ELM分类器的训练精度随隐含神经元数量的增加而增加，在隐含神经元数量为90时达到最大。测试精度一开始随着隐含神经元数量的增加而增加，当隐含神经元达到一定数量后，测试精度开始逐渐降低。因此，在三类睡眠分期实验中，隐含神经元数量在80～90区间时测试精度达到最大。所以，在三类睡眠分期实验中，若不对隐含神经元数量进行寻优选择，则统一设定隐含神经元数量为90。

图5 ELM分类精度变化

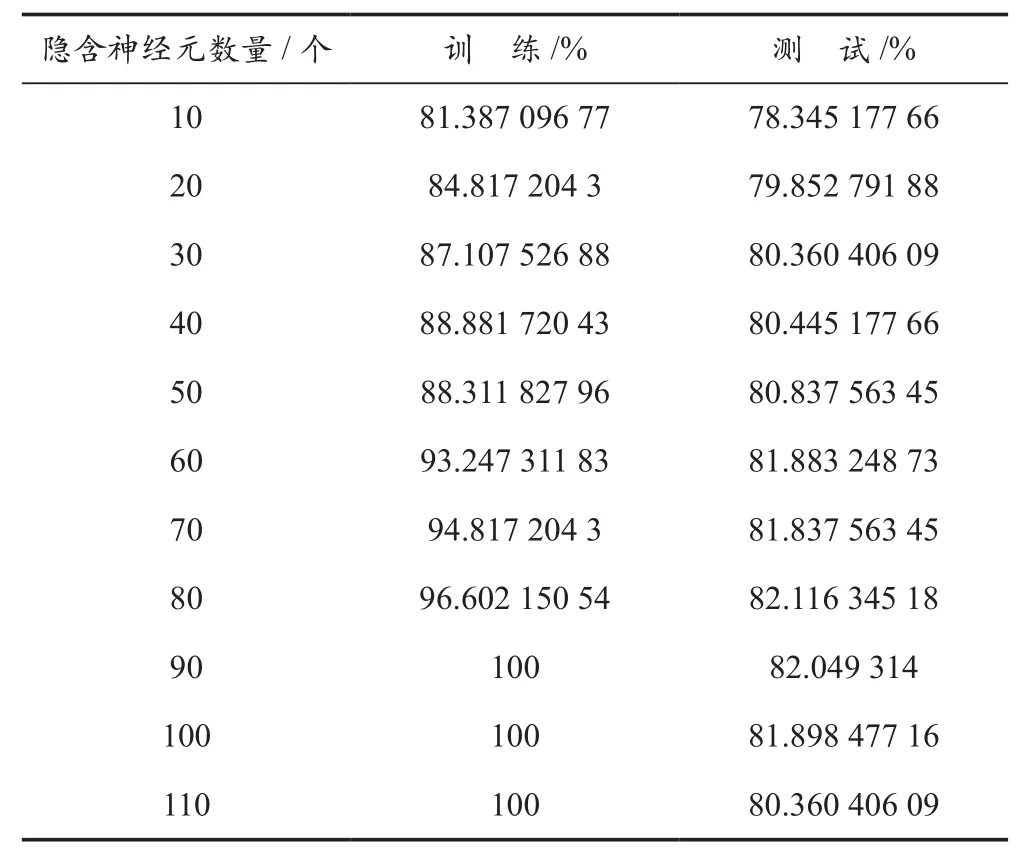
表4 ELM隐含神经元数量训练、测试时的精度

2.3 原始特征空间中分类

为能有效评估ELM分类器在原始特征空间中对睡眠信息进行分类的有效性和优越性，进行了以下实验。

利用ELM分类器、SVM分类器以及BPNN分类器分别建立三类睡眠分期模型，并将这3个模型得到的结果进行比较。实验结果见表5所列。

表5 原始特征空间中分类结果

从表5中可以看出，基于ELM睡眠分期模型的分类结果明显优于SVM和BPNN睡眠分期模型的分类结果，并且所耗费的时间也最短。此外，在SVM睡眠分期模型中，训练集和测试集间的精度误差高达29.09%，存在严重的过拟合现象。而在ELM睡眠分期模型中，训练集和测试集间的精度误差为7.62%，虽然也存在一定的过拟合现象，但并不严重。可以证明，ELM分类器相较于SVM和BPNN分类器，能够更有效的对睡眠信息进行分类。

2.4 基于特征选择的分类

在上述实验参数不变的情况下，利用PSO算法对ELM和SVM睡眠分期模型中的特征数量进行寻优，从而验证通过选择有效的特征数量能够提升睡眠分期模型精度的结论。其中，PSO算法中的参数设置：c1、c2设置为2，wA和wF分别设置为0.95和0.05，粒子的数量设置为30，共进行25次实验，选择其中分类效果最好的一次为最后的实验结果（实验结果加粗显示）。表6和表7分别给出了PSO算法优化ELM和SVM睡眠分期模型进行特征寻优的过程。

表6 PSO算法寻优ELM睡眠分期模型特征参数过程

表7 PSO算法寻优SVM睡眠分期模型特征参数过程

由表6和表7可以清楚看出，可以通过PSO算法对模型中的特征进行寻优选择，从而提升模型的分类精度。这说明，原始特征空间中并不是所有特征数据都是必要的，使用了不必要的特征反而会降低模型的分类精度。此外，相比较表5中ELM和SVM睡眠分期模型的分类结果，利用PSO算法对模型特征进行优化后，训练集与测试集间的精度误差明显降低，尤其是SVM睡眠分期模型，从原先的29.09%降低至2.12%，过拟合现象得到明显缓解。

2.5 基于特征与隐含神经元个数选择分类

通过表4可知，ELM三类睡眠分期模型最优的隐含神经元的个数在80至90之间。为了能够进一步提高睡眠分期模型的精确度，利用PSO算法在ELM睡眠分期模型进行特征寻优的基础上增加对隐含神经元个数的寻优，寻优过程见表8所列。对比表6和表8的结果可以看到，对隐含神经元个数进行进一步寻优后，ELM睡眠分期模型的整体精度从86.28%提升至87.11%，测试集与训练集间的误差从3.72%降低至3.41%。虽然变化不大，但仍然可以说明利用PSO算法优化ELM睡眠分期模型的有效性。

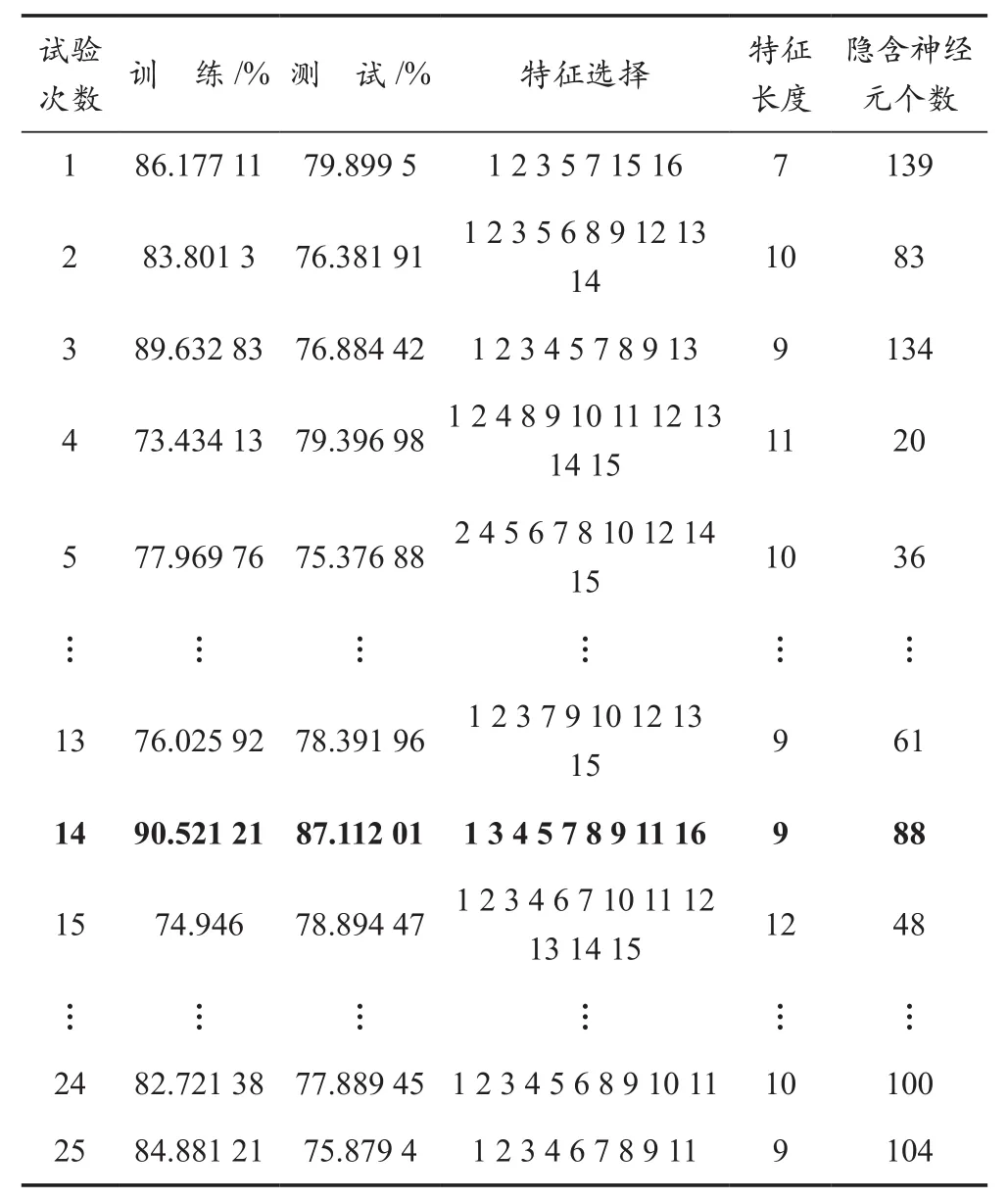
表8 PSO寻优ELM特征参数和隐含神经元个数过程

此外，表9给出了在4种不同睡眠分期状态下，SVM睡眠分期模型、PSO-SVM睡眠分期模型、ELM睡眠分期模型以及PSO-ELM睡眠分期模型之间的对比。实验证明，无论是在哪种睡眠分期状态下，利用PSO算法对SVM睡眠分期模型和ELM睡眠分期模型进行优化后，均可提升模型的精确度，并且能够有效缓解过拟合现象。

表9 4种睡眠分期模型对比

2.6 模型对比

从上述实验可知，PSO-ELM睡眠分期模型具有优秀的表现力，以三类睡眠分期的PSO-ELM模型为基础，与已有的基于心电和呼吸信号的睡眠分期方案进行比较。为保证实验的有效性，使用在同一数据集下的数据，用文献中提出的不同方法对ECG信号和呼吸信号的特征进行提取和建模，并与本文所提方法相比较，结果见表10所列。许良[9]提出用HMM-BP模型对睡眠进行分类，这种方法在睡眠的NREM期能得到较好的判别效果，但在REM期的表现不佳。李涛[10]利用LSSVM的方式对所提取特征进行建模分类，这种分类方式在睡眠的NREM期表现不错，准确率达86.58%，但在WAKE期和REM期的准确率均不超过80%。本文提出的PSO-ELM睡眠分期模型在WAKE期、REM期以及NREM期的准确率均超过80%，NREM期的准确率达88.96%。由此可以看出，PSO-ELM睡眠模型相比较现有睡眠分期方案具有一定优势。

表10 不同睡眠分期方案比较

3 结 语

睡眠分期是研究睡眠障碍和相关疾病的重要客观指标，为提高睡眠分期模型的准确率，本文提出了基于粒子群优化极限学习机的睡眠分期方法。实验结果表明，粒子群优化算法结合极限学习机对数据特征进行寻优，并对ELM的输入权值和隐含层神经元的阈值进行寻优，这种方法相比ELM模型而言，在睡眠分期的准确率上均占有明显优势，并且在一定程度上能够缓解模型的过拟合现象，是一种有效的睡眠分期模型，具有良好的应用前景。