基于复杂网络的通信工程专业课程体系分析

马金龙,张俊峰，张建燕，刘立萌

(1.河北科技大学 信息科学与工程学院，河北 石家庄 050018；2.中国联合网络通信有限公司河北雄安新区分公司，河北 容城 071700)

一、引言

“新工科”建设是基于国家发展战略部署、新旧增长动能转换和产业转型升级优化的新要求而提出的高等工程教育改革方向[1]。在“三新”(新技术、新业态、新产业)背景下，对工科人才创新创业能力有了更高的要求，迫切需要加快工程教育改革创新，培养一大批创新型卓越工程科技人才。

地方高校在“新工科”建设过程中，积极开展对新兴工科专业的研究与实践，结合新工科的新要求，加快传统工科专业的升级改造，在总结自身工程教育发展的历史中，找准定位，发挥自身专业发展优势，创新人才培养[2]，教育教学改革正在如火如荼的进行中。但是目前工科的课程教学依然存在诸多问题[3]-[9]，尤其是课程体系的构建，极大地影响着“新工科”人才的培养[10]。

第一，缺乏整体课程体系的全面认识。通信工程专业的通识课、必修课和选修课是一个有机的整体。由于专业课的教师在教学过程中往往只注重自己讲授的课程，忽视了学生对专业的整体认识，在学生对专业了解较少的情况下，直接一门课程接一门课程的学习专业知识，使学生头脑中不能形成完整的结构化知识框架，不了解所开设的课程在所学专业知识体系中的地位与作用。

第二．教学内容设置不灵活。在教学内容安排的过程中，专业课教师很大程度上依赖于教材和原有的教学经验，未能及时发现在教学内容中存在的不足，如：课程内容存在重复、冗余情况，课程顺序设置不合理等。

第三，理论与工程实际脱节。当今社会，新的理论、新的技术层出不穷，特别是对于信息工程领域，新的技术模式、新的智能仪表不断出现。但是专业的教学内容和课程体系却并没有发生变化，难以让学生掌握日新月异的新知识和新技术。

针对这一系列问题，本研究将复杂网络理论引入到通信工程专业课程体系的分析中，对通信工程专业知识网络的拓扑结构和统计特性进行分析，并结合通信工程专业教学实际问题进行探讨。Gephi软件对数据的各种操作和显示，不仅包括对拓扑网络中的节点、边和标签进行调整(着色以及大小的调节)，而且Gephi软件内的实时的布局算法可以对数据进行各种各样的布局[11]。借助Gephi软件将通信工程专业课程体系以拓扑结构的形式直观表示出来，使学生能够系统了解本专业课程之间的关系及其整体知识结构体系，避免了缺乏引导的机械学习，具有一定的理论和实践价值，同时在教学上可以为教师提供参考，为教学改革提供了新的方法和思路。

二、通信工程专业课程网络建模

本研究的对象是通信工程专业课程体系，将河北科技大学通信工程专业的各门课程建模成网络节点，并以课程之间包含的知识点关联以及先后学习关系为基础，找到课程两两之间的连边关系，建立通信工程专业课程网络。通信工程专业包含27门课程(见表1)、110种关系，即课程网络有27个节点、110条边。

表1 通信工程专业的27门课程

把表1中的所有课程之间的关系在Excel表格中整理成文本形式的数据资料，然后导入Gephi软件进行可视化展示，可以得到27个节点、110条边的网络模型，为了让网络看起来更直观形象，对课程网络进行外观和布局的设计。在外观上，将每个课程名称标注在相对应的节点上，将节点大小按照每个节点度值的大小调整，节点的度值越大，对应的视觉大小就越大。本网络为有向无权网络，网络中所有的边权重都为1。节点的颜色，按照节点度的大小来填充，采用的是深浅渐变颜色，节点度值越高，节点颜色越深。在布局方面，本网络采用了Fruchterman Reingold布局，建好的通信专业课程关系网络模型如图1所示。

图1 通信工程专业课程关系网络模型

三、基于统计特性的结果分析与讨论

度、集聚系数、介数和平均路径长度可用于分析网络的结构特征[12]-[14]。在本研究中，使用这4个参数分析通信工程专业课程网络。我们利用Gephi软件，对网络的特征参数进行统计，并基于网络参数对实际课程体系网络进行特征分析。

(一)基于节点度特性的网络分析

网络G可表示为G=(V,E),其中V={v1,v2,…,vn}是网络中节点的集合。E={eij|i,j=1,2,…,n}为网络中节点之间连边的集合，eij为节点vi和vj之间的边。网络G可以用n阶邻接矩阵A来表示，aij为A中的元素。当节点vi和vj之间有连边时，aij=1。没有连边时，aij=0。

网络中节点的度是指一个节点连边的条数。由于课程网络的节点之间的连边是由课程包含知识点的先后学习顺序所确定的，所以任意2个节点之间的连边是有方向的，建立的课程网络为有向网络。在有向网络中，度按照进入节点和离开节点分为入度和出度两种，进入该节点的边的数目称为该节点的入度，离开该节点的边的数目称为该节点的出度。

节点vi的度，入度、出度和有向图的邻接矩阵的关系如式(1)(2)(3)所示。

(1)

(2)

(3)

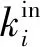
节点的度大小直接反映该节点(课程)在体系网络中的重要性，所以学习者应该将大度所对应课程作为重点学习对象，对这些课程的讲解也成为学科建设的重要任务。在本研究中，出度较大的节点对应的课程表示该课程是其他课程的先导课程的重要程度，入度值较大的节点对应的课程表示该课程是其他课程的后续课程的重要程度。对所建立的通信工程专业课程体系网络模型中的各个课程的度、入度、出度进行了统计，计算度比较大的前8门课程(见表2)。在表3和表4中，分别统计出了通信工程专业课程中入度和出度最大的5门课程，结果表明：入度较大的5门课是技能型专业课(通信原理、光纤通信、数字信号处理、信号与系统、电磁场与微波技术)，出度比较大的5门课多是数学类的公共基础性课程(高等数学、信号与系统、电路、线性代数、概率论与数理统计)。可见公共基础性课程是技能型专业课的先导课程。

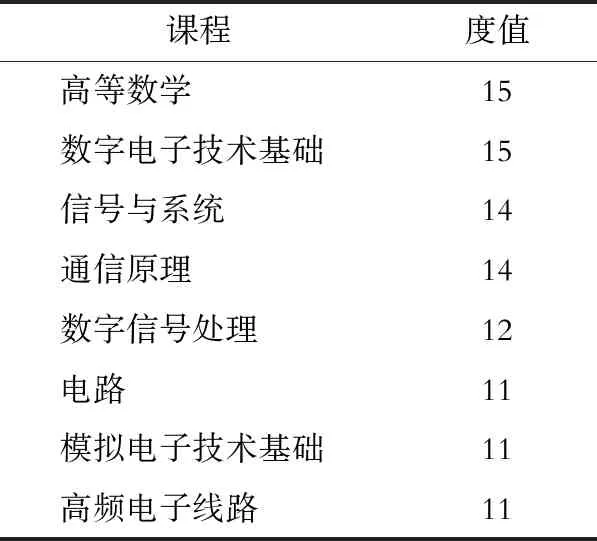
表2 通信工程专业课程网络中度最大的8门课程

表3 通信工程专业课程网络中入度最大的5门课程

表4 通信工程专业课程网络中出度最大的5门课程

(二)基于聚集系数特性的网络分析

网络聚集紧密程度可用聚集系数来描述。不同网络具有不同的聚集系数。在无向网络中节点的集聚系数公式为

(4)

有向网络中节点的集聚系数公式为

根据模糊评价矩阵 C=［C1，C2，C3，C4，C5］=·R，计算并进行归一化处理得出石油安全模糊评价矩阵 C=［0.068 5 0.128 8 0.554 6 0.175 4 0.0727］。将1996—2017年石油安全评价指标标准化数据与石油安全等级灰色统计数相乘，并进行归一化处理，由最大隶属度原则可得出1996—2017年中国石油安全状态，见表8。

(5)

其中ki是节点vi的度，Mi为网络中实际存在的边数。

平均聚集系数计算公式为

(6)

利用Gephi软件不仅可以统计出整体网络的平均聚集系数，还可以统计出每个节点的聚集系数。通过Gephi软件计算得出通信工程专业课程网络的平均聚集系数为0.267，并对每个节点的聚集系数进行了统计(见表5)。如果任意一门课程的聚集系数远大于该网络的平均聚集系数，就可以说明该门课程与其相邻课程彼此之间关联比较紧密。

表5 通信工程专业课程的聚集系数

以计算机通信网为例：计算机通信网的聚类系数最大，说明计算机通信网的邻居课程(大学计算机基础、C语言程序设计、计算机通信网、微机原理及应用、通信原理)彼此之间关联最为紧密。在教学方面，可加强这些课程协同教学工作。

(三)基于介数特性的网络分析

网络中所有的最短路径的条数与经过这个节点的最短路径数的条数之比定义为节点介数。介数Bi的计算公式为

(7)

其中Njl是节点vj和vl之间最短路径的数目，Njl(i)是节点vj和vl间最短路径并且同时经过节点vi路径的数目。

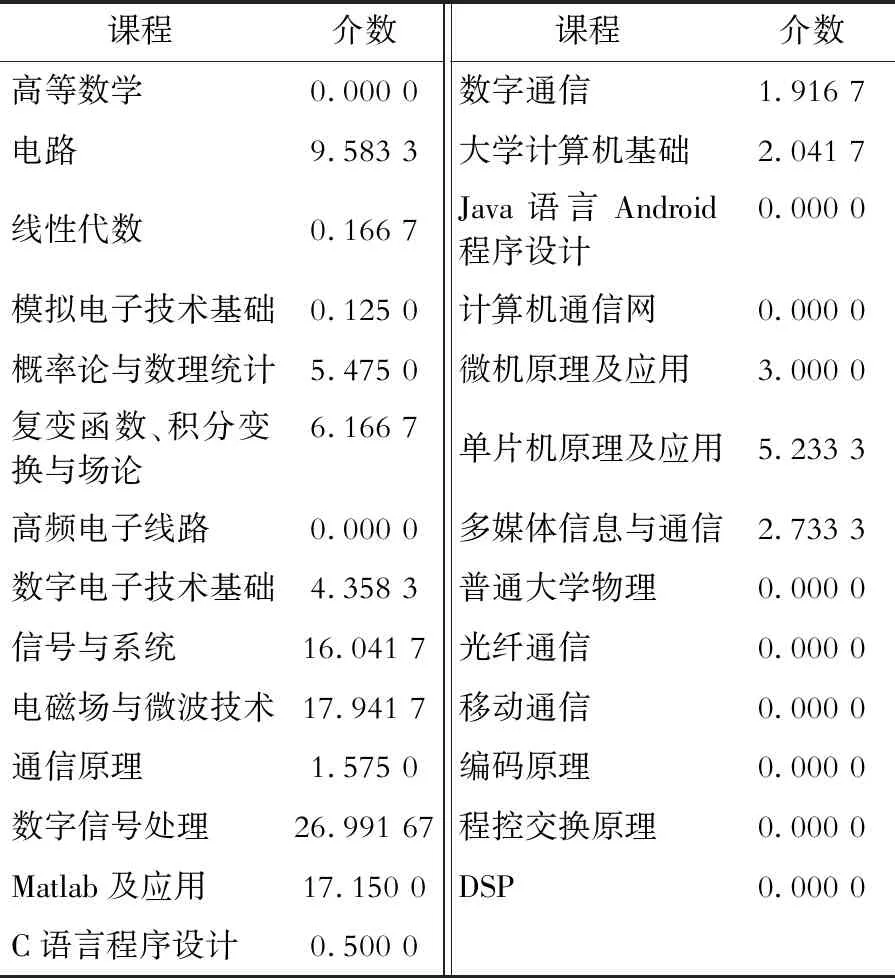
表6 通信工程专业课程网络的节点介数

(四)基于平均路径长度特性的网络分析

有向连通网络的平均路径长度L是指网络中所有节点和节点之间距离的平均值，见式(8)。

(8)

其中，dij代表节点i到节点j的距离，N代表网络中节点的数目。

任意两点之间的距离又称为两点连接的最短路径，2个节点之间存在最短路径就说明这2个节点是连通的，即可达的，平均路径长度是复杂网络用来研究网络连通性的一个重要统计特性。

本研究通过采用Dijkstra算法[15]对通信专业课网络的平均路径长度进行了计算，求得平均路径长度为1.55，由此可以得出结论：该网络中任意2门课程之间最短路径小于2，且1个网络中平均路径长度越小，网络连通性和可达性越强，所以该网络具有较强的连通性和可达性。

在表7中，统计了删除单个课程(节点)，路径减少数量最多的11门课程，路径减少的越多，说明该节点代表的课程与其他课程关联越复杂，但是考虑到此统计效果和平均度的统计效果类似，意义也相近，所以本课题再次统计了当删除1个节点时，总体网络平均路径长度的变化。在整体课程网络中删除1门课程，以及去除与该课程节点相连的路径，会增大整个网络的平均路径长度，如此就可以检验单独1门课程对整个网络连通性的影响。1门课程如果被删除后，平均路径长度增长的越大，表示该门课程越重要，即课程被删除后对课程网络的破坏性越大，表8整理了删除单门课程后平均路径长度增长最多的11门课程排序。据此可以清晰得出重要程度排名前五的课程为：数字电子基础、概率论与数理统计、高等数学、电磁场与微波技术、单片机原理，说明这些课程是学好专业知识的关键课程环节。

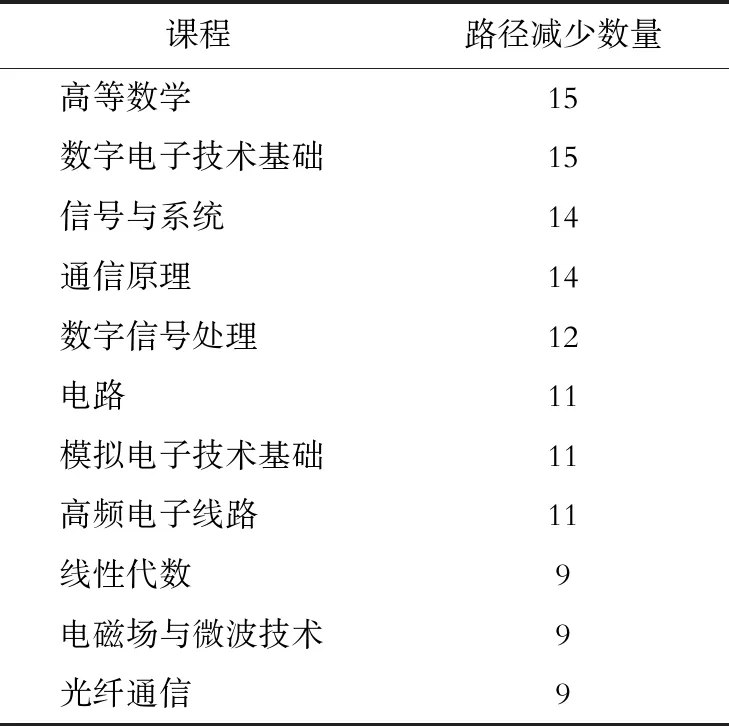
表7 删除后路径减少最多的11门课程

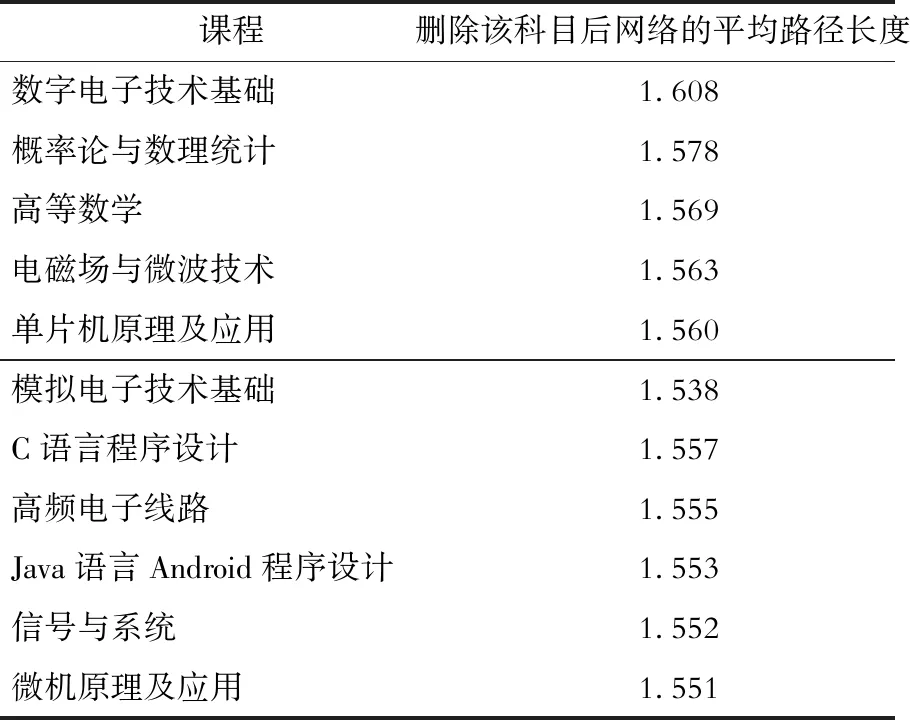
表8 删除单门课程后平均路径长度增长排序

(五)专业课程体系社团划分法

复杂网络的社团结构，简单来说就是指一个个的集合组成整体网络。集合即社团划分时将距离较近、综合特性比较接近或者相似程度较高的节点聚集在一起，这样的聚集点就形成一个个社团[16][17]。社团划分过程中，首先需要用到Gephi软件中的统计工具模块化，统计结果中可以发现数据资料多了一列数据Modularity Class，能明显看出27个节点被模块化成了3种类别，不同类别分别对应0，1，2(见表9)。

表9 课程模块化分类

接下来进行外观调整，采用Modularity Class渲染方式自定义社团划分的颜色，属于同一社团的节点被渲染为同一种颜色，运行之后社团划分拓扑结构即可成型。如图2所示，本研究将整个通信工程专业课网络划分成了3个社团，其中每个社团内部的节点连接比较紧密，在仿真软件里无论移动的哪一个节点，它仍然会自动恢复回去原来的位置，这中间似乎有一种吸引力牵引着每个社团中的节点。然而社团之间即不同颜色的集合节点连接相对稀疏，说明社团中每门课联系比较紧密，不同社团之间的科目联系比较少。在设计课程培养方案时，应加强模块内部之间课程教师的交流合作和协同教学。

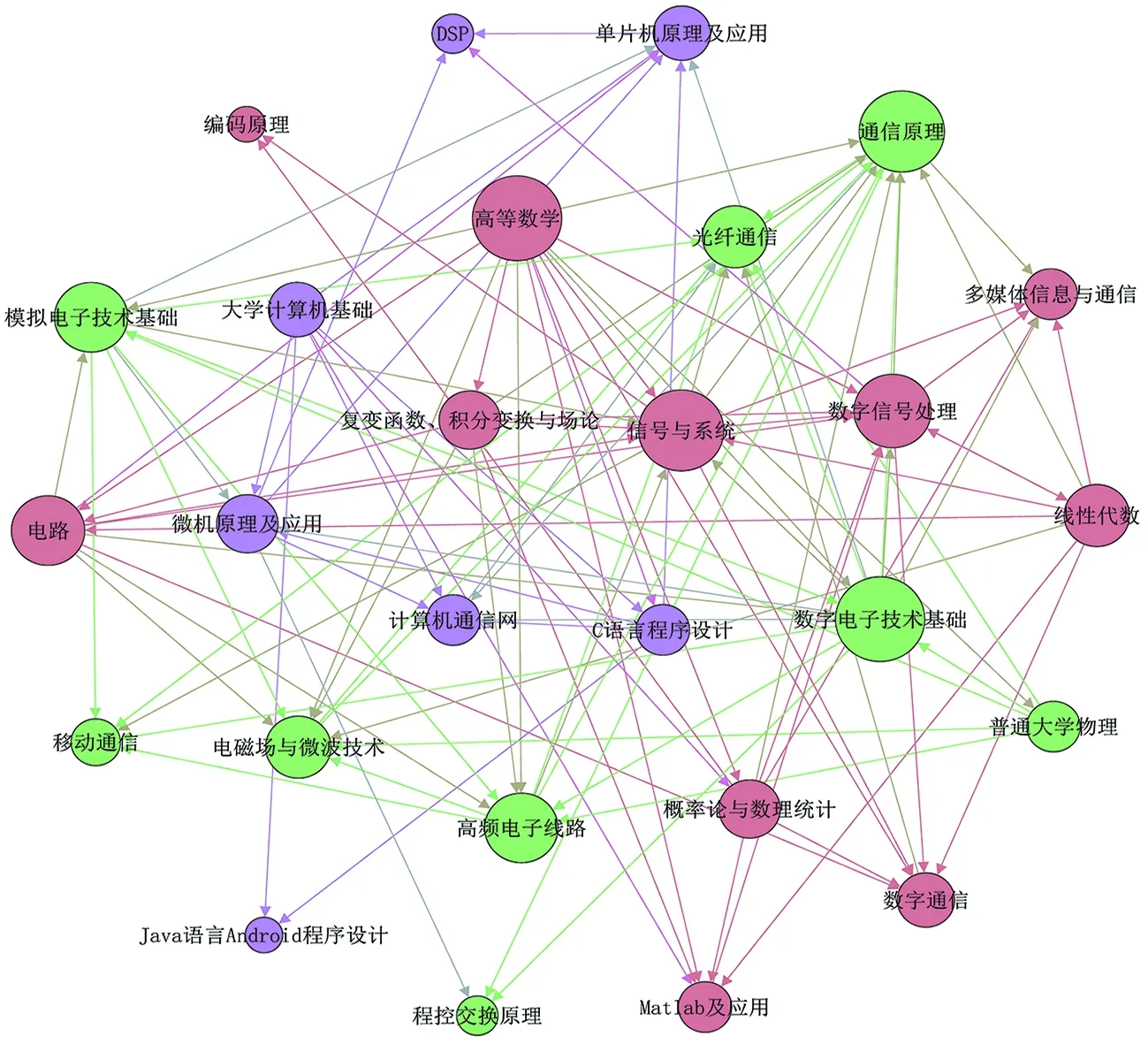
图2 通信工程专业课程网络的社团划分

社团划分这种拓扑结构也是一种统计特性工具，比不进行社团划分的初始网络更有利于清晰明了地看出课程之间联系紧密程度，同时更有利于进一步开发复杂网络的其他功能。所以说基于复杂网络社团结构理论对课程体系的深入研究不仅具有十分重要的研究意义，还具有广泛的应用前景。

四、结语

本研究结合教学大纲和大学生本科课程表对通信专业课程体系网络的节点进行了选取，以知识点之间的教学步骤为基础，建立课程之间关联，对课程网络的所有的有向连边进行了确定，将课程及课程之间的关系转化成Excel表格文本数据并导入Gephi软件，以河北科技大学通信工程专业为例构建了有向课程网络。然后，利用复杂网络的统计理论对通信工程专业课程网络的特性进行了统计计算，就计算出的结果进行了深入的分析研究。最后将分析结果与专业课程的教学实际相结合，和高等院校教学课表相比较，提出对教学改革的建设性建议。针对通信工程专业课程体系中各科课程重要性的分析，度、介数和平均路径长度变化量可用来衡量课程的重要性，重要性排列靠前的课程，应进一步提升其重要性。针对通信工程专业课程体系中各科课程的教学顺序分析，入度较大的课程是多数其他课程的后续课程，出度较大的课程是多数其他课程的先导课程。针对通信工程专业课程体系的课程分类分析，可根据聚类系数设计准确的社区划分方法，利用社区划分方法将课程划分为不同的培养模块。

“新工科”建设背景下，基于复杂网络理论的通信工程专业课程教学改革不仅实现了对课程授课和学习顺序的验证及调整，也为当前的高校教学改革提供了有效工具，更为复杂网络在课程优化领域的应用研究提供了一定的支撑和基础。