基于CNN的机载气象雷达气象目标检测方法
喻庆豪, 吴 迪, 朱岱寅, 钱 君
(1. 南京航空航天大学电子信息工程学院雷达成像与微波光子技术教育部重点实验室, 江苏南京 211106;2. 中国航空工业集团公司雷华电子技术研究所, 江苏无锡 214063)
0 引言
机载气象雷达是一种实时预报降水量的遥感设备。实际应用中,雷达一般工作在下视模式。当雷达天线方向图主瓣或旁瓣照射到地面时,来自地面物体的散射回波往往会湮没气象目标信号,严重影响气象参数的准确估计,从而恶化机载气象雷达的工作性能[1]。回波中的强地杂波背景在目标检测过程中会产生大量的虚警,增加了气象目标检测的难度[2]。因此气象目标的识别是必不可少的。
解决气象目标检测问题,通常需要以下两个过程[3]:1) 结合时域、多普勒域和俯仰维空域的相关信息,计算可区分气象目标与地杂波的判别函数;2) 根据判别函数设计性能较优的分类器,实现气象目标检测。目前已有文献利用地杂波和气象目标在谱矩信息方面的差异,设计了针对地基气象雷达的目标检测函数。由于静止地物目标后向散射回波在慢时间域的相位具有低可变性[4],杂波相位对准(Clutter Phase Alignment, CPA)技术利用此特性实现对气象目标的判别。相位起伏指标(Phase Fluctuation Index,PFI)和相位结构函数(Phase Structure Function,PSF)根据相邻采样脉冲间相位的变化快慢程度区分地杂波和气象目标。与固定地杂波相比,气象目标回波的相位变化更快[1,5]。谱杂波识别(Spectrum Clutter Identification,SCI)算法利用四种判别函数,即谱功率分布(Spectral Power Distribution, SPD)、谱相位起伏(Spectrum Phase Fluctuation, SPF)、功率纹理(Power Texture, PT)和谱宽纹理(Spectrum Width Texture, SWT),结合时域和频域信息实现对地杂波和气象目标的判别[6-8]。
除判别函数外,分类器的设计也是一项重要的工作。一般来说,模糊逻辑方法定义了极化变量和特定类型的水凝物之间的非线性关系,利用此非线性关系实现水凝物分类[9-12]。然而,模糊逻辑方法的检测性能并不稳定。此外,贝叶斯分类器、K近邻(K-Nearest Neighbor, KNN)算法,支持向量机(Support Vector Machine, SVM)和CNN同样可应用于气象目标检测中[1,5,13-18],而且国内外学者已经证明以上分类网络在图像识别和图像分类等方面具有明显的效果[3,19-22]。
本文提出了一种基于CNN的气象目标检测方法。该方法利用垂直阵列系统获取气象目标的俯仰维信息,并根据双通道雷达回波数据计算干涉相位。然后将CPA、多普勒速度和干涉相位作为三种判别函数一同输入到分类器中,进而得到最终的检测结果。仿真结果表明,该方法比传统的判别函数方法具有更好的检测性能,而且CNN比传统的分类器具有更好的鲁棒性。
1 基于CNN的气象目标检测方法
本文方法的整体处理流程如图1所示。本文选用CPA、多普勒速度和补偿后的干涉相位作为判别函数,在进行气象目标检测前,应先设计合适的CNN分类器,即设计CNN的网络结构,并使用合适的数据作为训练集数据对CNN进行训练至模型收敛,并能在验证集数据中有理想的准确率和损失结果。
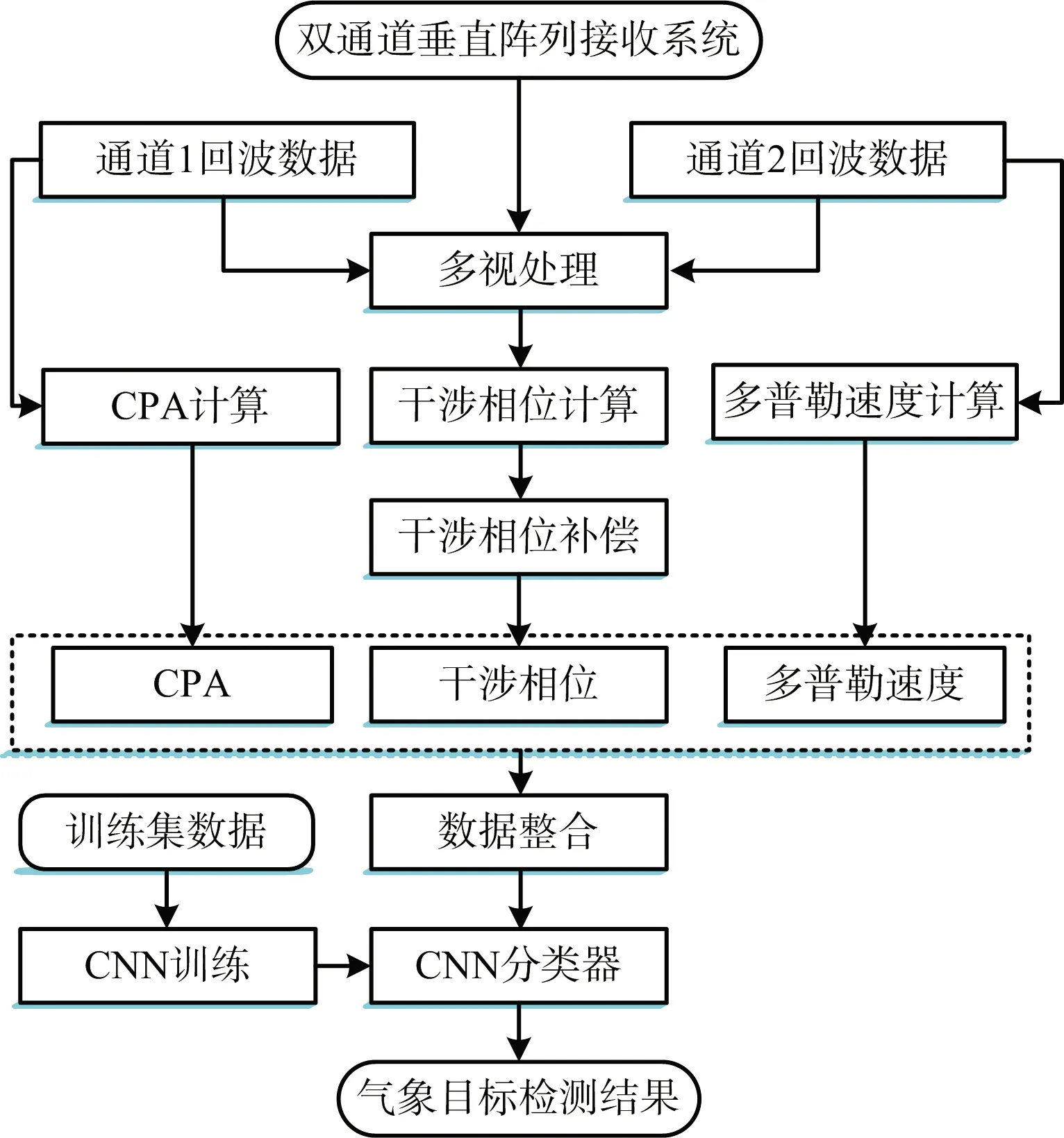
图1 基于CNN的气象目标检测方法流程图
在气象目标检测时,首先通过垂直阵列接收双通道雷达原始数据,通过多视处理和干涉相位补偿得到待检测的干涉相位数据,并根据回波计算CPA和多普勒速度。并将上述三种指标作为判别函数,并整合成适合CNN输入的数据形式,再输入到训练好的CNN中即可得到气象目标的检测结果。
2 判别函数的选择
2.1 CPA


2.2 多普勒速度
本节利用脉冲对处理法(Pulse Pair Processing, PPP)通过回波提取多普勒速度信息。脉冲对处理法不需要知道整个多普勒功率谱的详细结构,在时域直接计算得到谱的统计特征值。
设回波幅度的复振幅为S(t)=I(t)+jQ(t),I(t)、Q(t)分别为S(t)的实部和虚部。回波信号中取样样本数为N,则样本自相关函数为

j(Qi+1Ii-Ii+1Qi)]
(1)
脉冲重复间隔为Tr的相继两个回波信号的相位差为
(2)
式中,arctan{·}是反正切函数算子。因此多普勒平均频率可估计为
(3)
地杂波分量的多普勒速度在0 m/s附近;而气象目标通常被认为是缓慢移动的目标,因此气象目标具有非零多普勒速度特性。因此多普勒速度有能力检测出地杂波中的气象目标。
2.3 干涉相位
与CPA和多普勒速度两种判别函数不同,干涉相位是一种基于俯仰空域的气象目标检测函数。为获取气象目标的空间高度信息,本文采用俯仰双通道系统采集雷达回波数据, 对应的二维空间几何接收模型如图2所示。在俯仰通道接收模式下,干涉相位与下视角(即空间位置)有关。因此,在干涉相位图中,由于地杂波和气象目标高度不同,二者对应的干涉相位值也会存在差异,因此可利用干涉相位区分气象信号分量和地杂波分量。

图2 二维空间几何接收模型
本文选择线性调频信号(LFM)作为发射信号采集雷达数据,散射点P接收的回波信号经解调后如下所示:
exp{jπk(τ-rs(t)/c)2}·
exp{-j2πfc·(rs(t)/c)}+n(t,τ)
(4)
式中,k为线性调频信号的线性调频率,Tr为脉冲持续时间,c为电磁波传播速度,η为信号幅度,rs(t)/c表示电磁波从发射机传播到点P再由点P反射回接收机的总时间。为了简化分析,将忽略信号中的干扰成分n(t,τ)。则经过距离向脉冲压缩的信号为
(5)
式中,sinc{x}=sin(πx)/(πx),其中第1部分为脉冲压缩后信号幅度,对于两个不同的接收机R1,R2,rs(t)可以被表示为
(6)
一般来说,双通道系统的回波信号是相同的,但在式(5)第2部分中的相位有所不同。因此两通道的相位差可以表示为

(2π/λ)·dsinθ0
(7)
式中,d表示阵元间距,θ0表示P点处的入射角。则对于地杂波的干涉相位可以表示为
φA1A2_C=(2π/λ)·dsinθc
(8)
需要注意的是,在实际应用中,气象信号在空间高度上的分布是不规则的,这就导致了入射角的变化。也就是说,气象回波是由多个入射角的回波叠加而成。由气象信号得到的干涉相位与天线方向图和气象场景的反射率因子有关。为了简化分析,在图2中假设气象回波数据来自恒定入射角。因此,纯气象信号的干涉相位计算如下:
φA1A2_W=(2π/λ)·dsinθw
(9)
根据图2中几何关系可知,设φA1A2_W+C为气象目标和地杂波的混合信号,则同一距离门内气象目标和地杂波混合信号的干涉相位取值范围是
(2π/λ)·dsinθw<φA1A2_W+C≤
(2π/λ)·dsinθc
(10)
对于垂直阵列系统,干涉相位与方位角无关。因此,在相同距离处,干涉相位在方位角上保持不变。干涉相位提供了判别哪些区域可能包含天气信号的信息。设双通道系统中和通道接收信号为SS,差通道的接收信号是SD,则待检测的干涉相位图可计算为
InP=arg{[SD+SS]·[SD-SS]*}
(11)
式中,[·]*为共轭算子,arg{·}表示相位运算符。对地杂波而言,探测距离的变化会引起下视角的变化,进而影响杂波的干涉相位值。因此需要逐距离门对由距离变化引起的固有相位差进行干涉相位补偿才可得到待检测的干涉相位值。假设探测距离为R,载机飞行高度为H,在此距离门处地面目标对应的下视角为θc,且sinθc≈H/R,因此干涉相位的补偿量为
PC=2πdH/Rλ
(12)
经过干涉相位补偿后,地杂波分量的干涉相位值会趋近于0,而混合信号的干涉相位值应偏离0。干涉相位利用气象目标和地杂波的空间高度信息不同来检测气象目标,可有效避免低脉冲重复频率(Pulse Repetition Frequency,PRF)对多普勒频谱展宽和多普勒模糊的影响。因此,根据补偿后的干涉相位,可利用俯仰空域信息实现气象目标检测。
3 CNN分类器设计
近年来,GPU计算能力的大幅度提升以及神经网络软件搭建网络框架的极大便利性,使得CNN在学术界和工业界越来越受青睐,CNN被广泛应用于图像分类,人脸识别等多个领域。因此,鉴于CNN强大的分类能力,本文利用此网络处理气象回波数据,实现对气象目标的检测。
本文将雷达回波数据预先处理成三种判别函数的形式,根据到CNN的卷积计算原理,将三种判别函数整合成一个三维数组。在处理过程中,CNN被视为滑动窗口检测器,需要在数据中逐像素点滑动并输出判断结果。将CNN的输入数据的大小设置为3×32×32,因此每个待检测像素点的最终检测结果取决于待测单元周围3×32×32的三维数据在CNN中的输出。
训练CNN网络,需要生成或是找到合适的数据作为训练集。训练集的原始数据需要先通过计算得到三种判别函数,并将其整合成三维数据,然后分成若干组3×32×32大小的数据,最后根据先验信息将这些数据分别赋予地杂波和气象目标的标签。为了防止每组数据主要由噪声像素点组成,用时为了使CNN有足够且有效的样本进行训练,这里选用至少一半像素点为气象或是地杂波的数据,而且为了使样本的选取更具有代表性,选择像素点的原始数据的幅度不应该太低。
利用CNN可以详细分析出所选的三种判别函数和两种回波数据之间的非线性关系。本文所设计的CNN模型的网络结构如表1所示,它由5个卷积层(Convolutional Layer),1个全连接层(Fully Connected Layers, FC)和2个最大池化层(Max-pooling Layer)组成,此网络选择线性整流函数(Rectified Linear Unit, ReLU)作为激活函数,同时为了改善流经网络的梯度,提高训练速度,在网络中设置批量归一化(Batch Normalization,BN)。将三维输入数据输入到网络中,通过每一层网络的处理和计算,最后通过Softmax函数计算气象目标和地杂波被取到的概率并与检测门限比较,输出最终检测结果。

表1 CNN结构及属性
4 实验结果与分析
本节利用仿真数据验证所提出方法的有效性,为此生成两组机载雷达仿真数据,主要参数见表2。为了训练前一节中设计的CNN,首先利用第一组数据作为训练集数据,使用该数据分别计算出CPA,多普勒速度和补偿后的干涉相位,并将三种判别函数的计算结果整理成三维数据的形式。

表2 仿真数据和实测数据对应的主要参数
为了证明这三种判别函数的特征选取是有效的,如图3所示,对训练集数据中的CPA、干涉相位和多普勒速度三维数据进行特征分类空间描述,图中,蓝色散点和红色散点的位置分别代表地杂波与气象目标对应的判别函数值在该三维空间中的分布情况。从图中可以看出,地杂波和气象目标对应的两种点迹在CPA-多普勒速度-补偿后的干涉相位构成的三维空间中有明显的界限,这可说明特征选取的有效性和正确性。
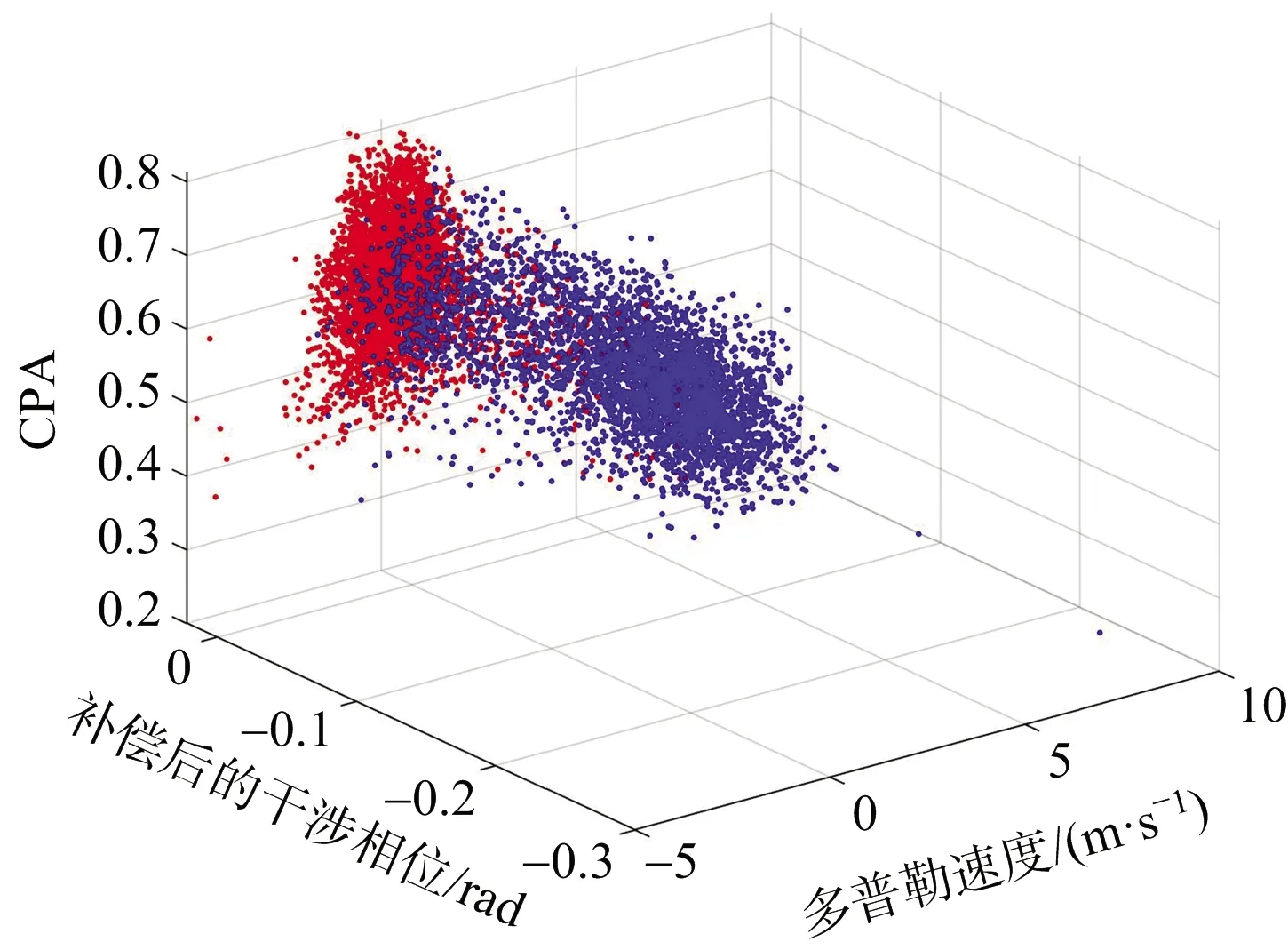
图3 地杂波与气象目标在三种判别函数空间中的分布
利用上一节提到的数据存储方式,从此三维数据中提取10 000组3×32×32大小的数据,标记为气象目标,同时提取10 000组数据标记为地杂波。然后从上述20 000组数据中随机选取14 000组作为训练集数据来训练CNN,余下6 000组数据作为验证集,以观察训练过程中准确率曲线和损失曲线的变化情况。训练过程中采用具有动量随机梯度下降法(Stochastic Gradient Descent with Momentum, SGDM)训练设计的网络,将epochs设置为15,学习率(Learning Rate)设置为0.01。经过训练,检测验证集的准确率可以达到99.60%,检测验证集的损失降低至0.021,此时额外的训练不会改进模型,CNN模型达到收敛状态。
训练好CNN后,就可以用CNN进行气象目标检测,图4给出了在测试集中三种判别函数的计算结果以及气象目标的真值图,真值图中,“1”表示含有气象目标分量的像素点,“0”表示只有地杂波分量的像素点。由于飞机运动带来的多普勒频移使得CPA和多普勒速度在数值上与理论值存在偏差,而在CNN的作用下测试中平台速度对分类结果的影响可忽略,不需要补偿多普勒信息,直接对原始回波进行分析即可。

图4 三种判别函数的计算结果及理论真值图
为了更直观地反映本文方法的检测性能,将正确分类为气象目标的像素点标记为TP,将错误分类为气象目标的像素点标记为FP。类似地,将正确分类为地杂波的像素标记为TN,错误分类为地杂波的像素标记为FN。在图5中,在信杂比为5 dB的情况下,将该方法检测结果与CPA、多普勒速度和PFI三种气象目标检测方法的检测结果进行比较。如图5所示,虽然本文提出的方法在信噪比较低的区域仍然有一些被误判为FP和FN的像素点,但具有最好的检测性能。由于飞机的运动,使得原始回波数据中的多普勒信息恶化。依赖于多普勒信息的CPA,多普勒速度和PFI等检测方法的性能明显较差。然而,本文提出的方法结合了多普勒域和空域的信息,在谱矩信息恶化的情况下仍可获得较好的性能。
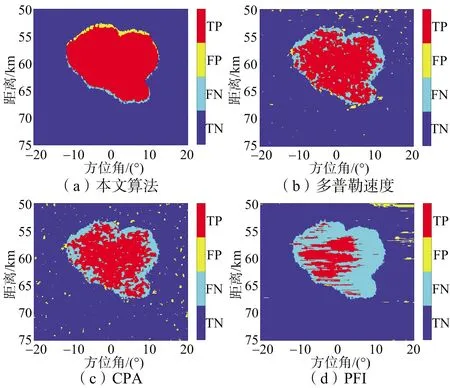
图5 利用不同方法得到的气象目标检测结果
进一步地,利用检测概率和虚警概率定量分析几种方法的性能,检测概率和虚警概率分别定义为
(13)
图6给出了在Pfa=0.001 4时,不同检测方法对应的检测概率随信杂比的变化关系。结果表明,相比于其他方法,所提方法在检测概率方面具有更优的性能。

图6 不同信杂比下各种检测方法对应的检测性能曲线
此外,为了验证谱矩特性对各种方法检测性能的影响,在合理情况下,设定信杂比为5 dB,分别改变地杂波的谱宽和气象目标的多普勒频移,得到图7和图8对应的检测概率曲线。可见,由于谱宽的增加,基于多普勒信息的气象目标检测方法的性能有所下降,而本文方法结合了多普勒信息和空域信息,有效降低了由谱宽增加带来的检测性能的恶化。而多普勒频移较低时,几种基于多普勒信息的检测方法的检测概率都不是非常理想,但本文方法在多普勒频移较低时,能够有比较高的检测概率;且在多普勒频移比较高时,本文方法的检测概率仍比另外几种算法更高,突出了本文方法的优越性。

图7 不同地杂波谱宽下各种检测方法对应的检测性能曲线

图8 不同气象目标多普勒频移下各种检测方法对应的检测性能曲线
为了突出CNN的优越性,使用相同的训练数据集来训练贝叶斯分类器和支持向量机,并用训练好的贝叶斯分类器和支持向量机对图5中涉及到的测试数据集进行了处理,检测结果如图9所示。结合图9和图5(a)的检测结果,可以看出,两种常规分类方法的检测结果中存在较多的FP和FN像素点。因此,采用CNN作为气象目标的分类器是一种较好的选择。

图9 使用不同分类器对应的检测结果
5 结束语
为检测强地杂波背景中的气象目标,本文提出了一种基于CNN的目标检测方法。该算法结合多普勒域信息和空域信息,将CNN作为分类器实现对气象目标的检测。文中详细讲述了该方法的实现流程以及CNN的具体结构,并通过仿真结果表明,该方法可有效用于气象目标的检测。与现有的大多数方法相比,该算法具有更优的检测性能,并能很好地克服谱矩信息变化带来的影响,具有一定的实用价值。

