联合时频分析和谱估计的机动目标ISAR成像
周子铂, 王鑫奎, 蔡万勇, 刘建卫, 张朝伟
(1. 空军预警学院, 湖北武汉 430019; 2. 中国人民解放军63696部队, 江苏江阴 214400)
0 引言
逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)成像作为微波成像领域的代表性技术,通过积累回波可以获得目标的微波电磁图像。具体而言,ISAR通过发射大带宽的信号获得距离向的高分辨,方位向的高分辨则由目标与雷达之间的相对转动实现[1-3]。对于匀速转动目标,传统的距离-多普勒(Range-Doppler, RD)算法在完成平动补偿之后就能得到比较清晰的目标图像。然而对于机动目标而言,同一距离单元内多个散射点回波的频谱易发生混叠,致使传统的RD成像方法获得的ISAR图像非常模糊。
此前,学者们已经提出了很多方法来解决机动目标ISAR成像的方位向散焦问题。机动目标旋转一般包含有加速度甚至加加速度,目标的旋转加速度产生二次相位项,高机动目标的旋转加加速度将产生三次相位项。因此,散射点回波的多普勒频率都是时变的[4-5]。文献[6]提出一种利用参数自相关方程和广义扩展傅里叶变换的参数估计方法来重构机动目标的距离-瞬时多普勒图像。鉴于机动目标方位向回波为多分量线性调频信号,自相关方程产生的交叉项致使ISAR图像质量恶化。由于目标回波多普勒频率的时变特性,能反映信号频率随时间变化的时频分析工具通常被用来获取高分辨的瞬时ISAR图像,一些有效的时频分析方法被提出。在文献[7]中,回波信号被建模为多分量的三次相位信号,综合利用距离-瞬时多普勒算法和距离-瞬时调频率算法获得高分辨的瞬时ISAR图像。文献[8]提出了基于距离-瞬时多普勒导数的机动目标ISAR成像算法,该算法通过多普勒频率的任意阶导数实现方位分辨,可视为传统RID算法和RIC(Range-Instantaneous-Chirp-Rate)算法的扩展。然而,上述算法中复杂的迭代参数估计步骤增加了算法负担并且会导致较严重的误差传导。
对于弱机动目标,上述算法一般可以产生高分辨的ISAR图像,但是对于强机动目标,受相干积累时间内方位向高阶相位的影响,上述方法成像分辨率会显著恶化。在相干积累时间一定的条件下,超分辨成像可有效提高ISAR成像的分辨率。鉴于多重信号分类(Multiple Signal Classification, MUSIC)谱估计算法在波达方向(Direction of Arrival, DOA)应用方面的高分辨特点,Odendaal等在文献[9]中首先提出利用Schmidt提出的空间谱估计方法来重构大转角条件下的二维超分辨雷达图像。南京电子技术研究所的凌牧等在文献[10]利用基于AR-CAPON联合谱估计的方法实现ISAR图像的超分辨,该方法对实测ISAR数据建立自回归(Auto Regressive, AR)模型,然后利用Burg算法求解AR模型进行数据外推,提高CAPON滤波器的长度上限,再利用CAPON算法进行超分辨ISAR成像。上述所述均为谱估计方法应用于普通目标,由于机动目标在成像时间内的复杂运动,将谱估计方法应用于经由时频工具处理之后的回波,不仅可有效避免目标机动对ISAR成像的影响,而且可克服小转角对方位分辨率的限制,进而获得机动目标的高分辨ISAR图像。
由于机动目标的方位向信号可被建模为多分量的线性调频信号,本文提出利用短时傅里叶变换(Short Time Fourier Transform, STFT)获得单个距离单元特定瞬间的频谱,进而减弱长成像时间内多普勒频率的时变特性。由于STFT的分辨率受限于“不确定性”原则,本文提出在对回波经过STFT处理之后,再利用MUSIC谱估计方法重构机动目标的高分辨ISAR图像。本方法不仅可以有效避免其他时频分析方法的交叉项影响,而且可以克服“不确定”原则对STFT分辨率的限制,进而可获得高分辨的ISAR图像。
1 ISAR成像模型
机动目标的ISAR成像模型如图1所示,XAY为雷达坐标系,A为目标的旋转中心,即雷达所在的位置。R0表示目标参考点O到雷达的距离;w,α分别表示目标旋转的初速度和加速度。θ表示目标的瞬时旋转角度:
(1)
此处,tm代表慢时间,目标上的任一散射点Qi到雷达的距离可表示为
R=R0+x0sinθ+y0cosθ
(2)

图1 ISAR成像模型
成像时间内的目标旋转角度通常较小(3°~5°),因此,有如下近似sinθ≈θ,cosθ≈1。进而散射点到雷达的距离可以表示为
(3)
Qi散射点的多普勒频率可以表示为
(4)
此处,λ表示雷达发射信号的波长。重构Qi散射点的相位如下:
(5)
此处,φ0代表初始相位。P表示一个距离单元内包含的散射点个数,在完成平动补偿之后,第l个距离单元的回波信号可以表示为多分量的线性调频信号[11]:
(6)
根据公式(5)和(6)可知,机动目标的慢时间域回波可以表示为多分量的线性调频信号,经过傅里叶变换之后,各散射点回波的宽带频谱会产生重叠。因此,传统RD算法获取的机动目标ISAR图像将是方位向散焦的。下面介绍本文提取的获取机动目标的高分辨ISAR图像的方法。
2 机动目标的高分辨ISAR成像
2.1 基于STFT方法的距离-瞬时多普勒成像
STFT通过截取信号的一小段并应用傅里叶变换获得此一小段信号的频谱,具体实现如图2所示。
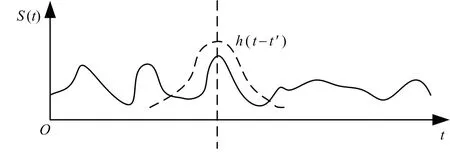
图2 STFT截取信号
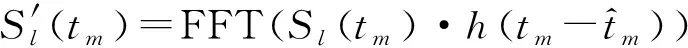
(7)


(8)
(9)
(10)
2.2 基于STFT方法的距离-瞬时多普勒成像
鉴于“不确定”原则对STFT时间分辨率和频率分辨率的限制,在窗函数截取信号使信号长度变短之后,频率分辨率变差,进而ISAR成像结果变得模糊。因此,此部分主要介绍空间谱估计方法对STFT结果的超分辨处理,克服“不确定”原则的限制。
如式(8)和(9)所示,在截取窗的短时间内,时间tm可以近似为常数,每个散射点的多普勒频率仅仅与散射点的横向坐标xi相关。可得第l个距离单元的回波可表示为
(11)

已知高分辨空间谱估计方法常用于波达方向(Direction of Arrival, DOA)估计,MUSIC估计方法可以估计得到多个信源的准确方位,类比可以将MUSIC估计方法应用于单个距离单元内散射点横向位置估计,即多普勒频率域的超分辨。首先,由式(11)可将第l个距离单元的回波以矩阵形式表示。由于慢时间维选取了N个脉冲用来成像,因此第l个距离单元的维度为N×1,如式(12)所示。

(12)

X=A·S+N
(13)

(14)
(15)
(16)
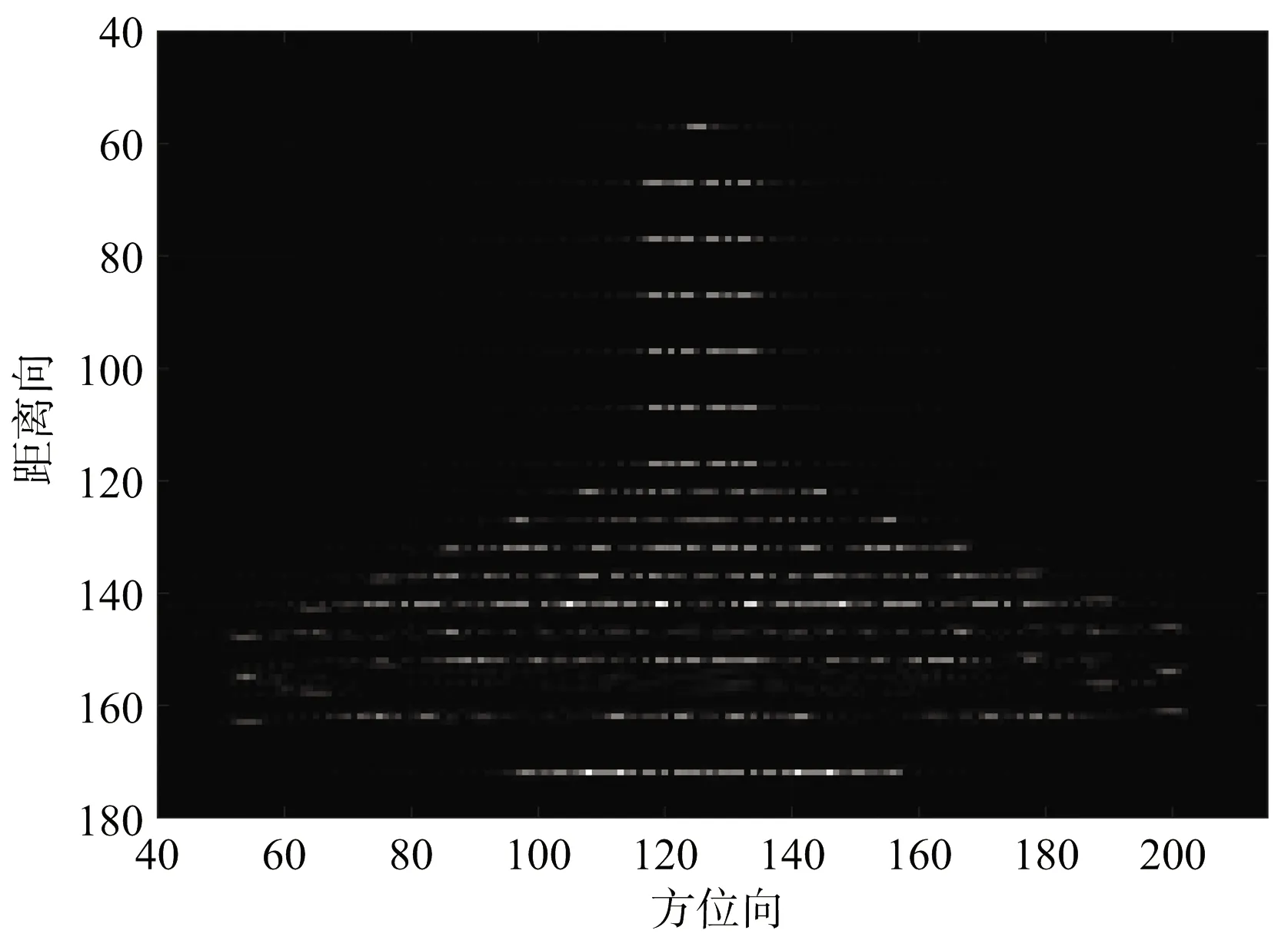
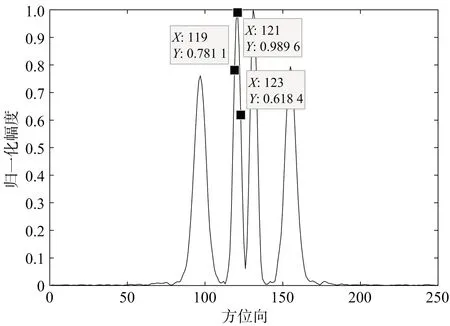
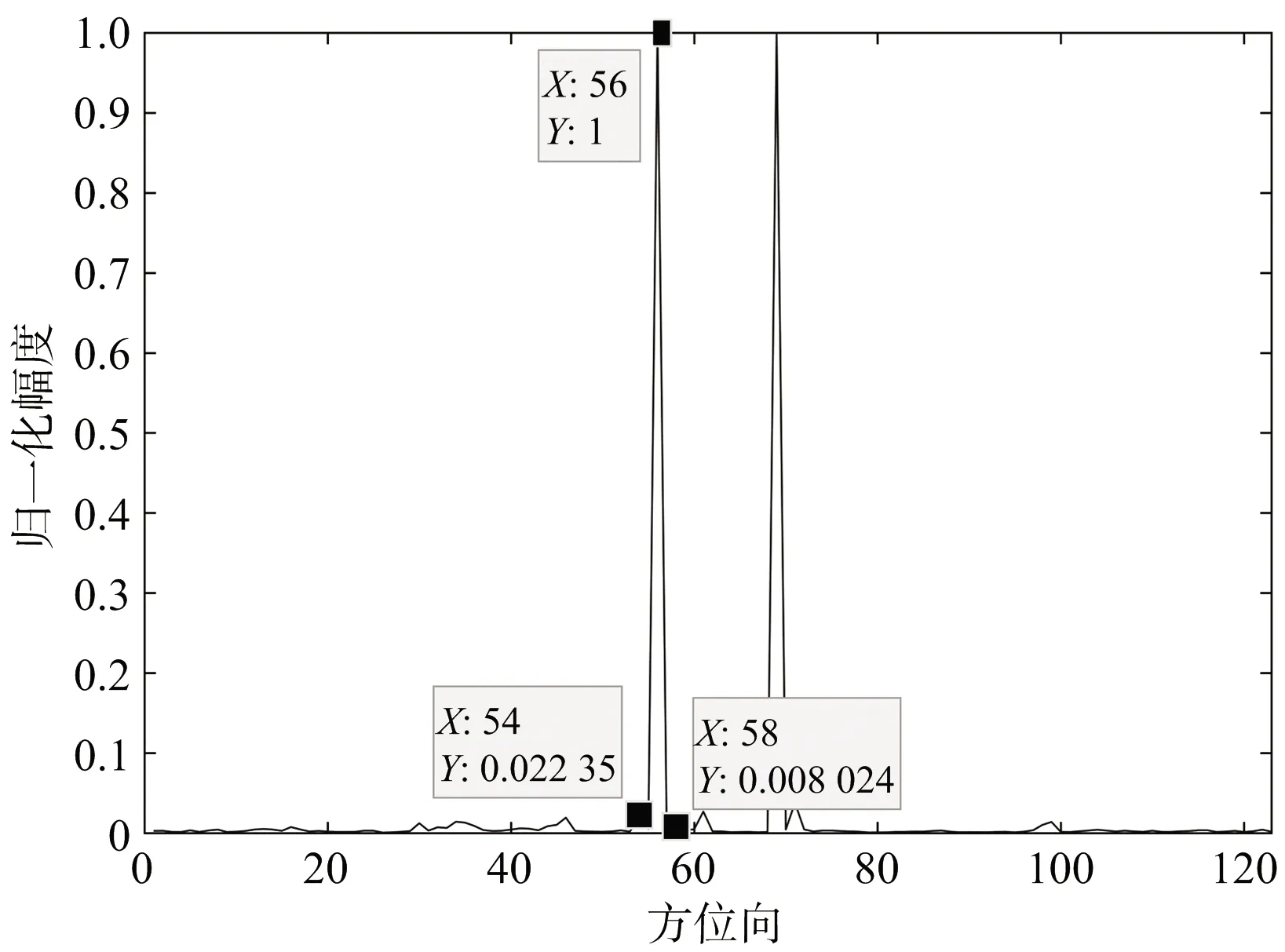
注意到,MUSIC谱估计方法用到了信号的统计特性,这需要多次数据采集来实现。不同于阵列天线可以在不同的时间获取多次快拍以获得信号的统计特性,ISAR成像仅有一次快拍,所以经典的MUSIC谱估计方法不能直接应用在此处。滑窗技术被用于解决此问题,以获得多次快拍,并消除回波之间的相干性,具体如图3所示。其中,滑窗的长度为(d×1,d (17) 第k个子矢量Xk的协方差矩阵可写作 (18) 此处H代表复共轭转置。完整回波矢量的协方差矩阵为 (19) (20) 图3 回波滑窗技术 MUSIC谱估计算法实现高分辨,是基于数据自相关矩阵信号特征子空间和噪声子空间的正交关系。协方差矩阵RXX可以分解得到N个特征值,从大到小依次为(λ1>λ2>λ3>…>λN),对应特征值的特征向量设为v。信号子空间由P个大的特征值对应的P个特征向量张成Vs=[v1,v2,v3,…,vP],噪声子空间则由剩余的N-P个小特征值对应的特征向量张成Vn=[vP+1,vP+2,vP+3,…,vN]。因此,协方差矩阵RXX的分解如式(21)所示: (21) 此处∑表示P个大特征值组成的信号特征值,因此∑为(P×P)维的对角矩阵。σ表示N-P个小特征值,噪声特征值可近似视为相等。最后,MUSIC的谱估计结果可由式(22)求解得到。在特定的范围内搜索散射点的横向坐标x,峰值出现的位置即为散射点所在的位置,相比于经典的傅里叶变换而言,基于MUSIC算法的空间谱估计算法能获得更好的频率分辨率。 (22) 步骤1 对所有回波进行距离压缩和平动补偿,得到方位向回波为 (23) 步骤2 对所有距离单元的方位向回波S(f,tm)进行STFT处理,并通过最小熵准则来选择聚焦效果最佳的多普勒频谱S(f,fm)。 上述为基于联合时频分析和MUSIC超分辨的机动目标ISAR成像算法,具体的算法执行流程如图4所示。 图4 算法执行步骤 本部分通过ISAR成像实验验证上述所提出方法的有效性,包含两组实验:散射点仿真模型和波音B727实测数据成像实验。雷达参数和仿真目标参数如表1所示。所有实验的成像模型如图1所示,并假设平动补偿已经完成。仿真散射点模型如图5所示。 表1 目标和雷达的仿真参数 图5 仿真模型 为形象准确分析目标机动对于回波多普勒频率的影响,此处先对第132个距离单元进行时频分析,分别采用STFT和魏格纳-威利分布(WVD)对其进行处理,具体两种算法获得的时频分布如图6所示。图6(a)表示STFT算法获得的时频分布图,图中显示包含有4条亮线,即表示包含有4个散射点,但是4条线在频率轴方向都比较粗,表明STFT获得的时频分布图的频率分辨率比较低,即为前面讲到的STFT分辨率受“不确定”原则限制。图6(b)表示WVD算法获得的时频分布图,根据WVD的定义可知WVD分布图包含很多交叉项,并且图中无法区分出明确的4条线,但是最外围的两条自项产生的时频分布线比STFT结果较细,即WVD可以获得较高的频率分辨率。然而,两个分布图都表示多普勒频率随慢时间逐渐变化,表明机动目标回波多普勒频率的时变特性。 (a) STFT计算结果 (b) WVD计算结果图6 第132个距离单元的时频分析结果 仿真散射点模型的机动目标成像实验的回波模型如图1所示,此时目标的旋转参数分别为:初始角速度为0.04 rad/s,角加速度为0.03 rad/s2。图7显示了4种方法的仿真模型机动目标成像结果。图7(a)为传统RD方法获得的机动目标ISAR成像结果,从图中可以看到由于目标的机动飞行,所成ISAR图像在方位维会产生严重的散焦现象。图7(b)和图7(c)为时频分析工具WVD和STFT算法所成的ISAR图像,在不同的窗长和时间点上对回波信号进行WVD或者STFT处理,然后根据最小熵准则选择聚焦效果最佳的一维方位像,最终组成所得到的ISAR图像。观察图像可见,一方面,由于WVD中众多交叉项的存在,在所成的ISAR图像中会产生众多对应的“假点”;另一方面,虽然STFT算法所获得的图像没有交叉项产生的“假点”,但是由于“不确定”原则的限制,STFT算法的方位向分辨率较差,最终导致所成ISAR图像也比较模糊,如图中白色圆圈部分所示。而且,根据图像可进一步观察到,散射点越远离目标的方位轴心,散射点在方位维的模糊现象越严重。图7(d)所示为本文所提新方法获得的ISAR图像,相比于上述三种成像方法,新方法获得的图像更加清晰,具体而言,白色圆圈内的模糊现象得到很好的解决。 (a) 经典RD算法成像结果 (b) WVD算法成像结果 (c) STFT算法成像结果 (d) 所提出方法成像结果图7 仿真模型ISAR成像结果 为进一步表明所提出的联合时频分析和谱估计成像方法可获得更好的聚焦效果,选取上述图7中的第132个距离单元,其归一化曲线图如图8所示,观察图像可知,此距离单元具体包含有4个散射点。图8(a)和图8(b)分别表示FFT和WVD的多普勒频率聚焦效果。因为FFT呈现的是回波的整个的多普勒频谱,由于目标的机动操作,各散射点的多普勒频率为时变的,即为宽带频谱,多个散射点的多个频谱发生混叠,最终多普勒频率聚焦效果被严重影响,导致4个散射点无法被完全分辨。另一方面,WVD的交叉项导致原本4个散射点的4个谱峰连接在一起,并且多个交叉项的叠加会产生伪峰,从而导致各散射点无法被完全区分,甚至产生“假点”。图8(c)和图8(d)呈现STFT算法和所提出算法的更好的散射点分辨效果。为具体说明MUSIC谱估计方法对于STFT算法的估计效果,图8(c)和图8(d)的第二个峰值(图8(c)中X=121,图8(d)中X=58)的宽度数据如表2所示。由表2数据可知,所提出方法的峰值下降速度比STFT算法的峰值下降速度更快,可以说明图8(d)中的峰值更窄,即所提出方法可以获得更好的方位分辨率。 (a) FFT算法聚焦效果 (b) WVD算法聚焦效果 (c) STFT算法聚焦效果 (d) 所提出方法聚焦效果图8 第132个距离单元的方位向聚焦效果 表2 仿真数据第二个谱峰的宽度 此部分,美国海军实验室的波音B727实测数据[13]被用来进一步实验验证所提成像方法的有效性。其中,回波的载频和带宽分别为9 GHz和150 MHz,脉冲重复频率为20 kHz,此处选择256个脉冲用于ISAR成像。目标回波平动补偿之后的一维距离像如图9所示。 图9 波音B727实测数据一维距离像 图10给出了4种方法对于波音B727飞机的实测数据成像结果。同样,图10(a)为传统RD算法获得的ISAR图像,显然由于目标的机动飞行,ISAR图像在方位向出现严重的散焦现象。然后,为克服散焦现象,WVD和STFT算法分别用来实现机动目标ISAR成像,如图10(b)和图10(c)所示。与上述散射点模型实验类似,WVD算法中生成的交叉项会产生众多“假点”,从而导致所成图像几乎无法识别出目标的轮廓。相比于WVD算法,STFT算法可以获得目标的图像,但是,鉴于“不确定”原则对分辨率的限制,且STFT中的滑窗降低了信号的长度,导致STFT所成图像在方位维分辨率较低,即各散射点依旧会在方位维产生模糊,如图10(c)中呈现的结果所示。由于MUSIC空间谱估计方法可以获得更好的频谱分辨率,所以MUSIC对STFT算法处理之后的回波进行谱估计可以克服“不确定”原则对频率分辨率的限制,获得更佳的ISAR成像结果,本文所提新方法的成像结果如图10(d)所示,并且所得图像比上述三种方法更佳清晰。 (a) 经典RD算法成像结果 (b) WVD算法成像结果 (c) STFT算法成像结果 (d) 所提方法成像结果图10 波音B727实测数据成像结果 同样,为进一步表明多提出方法对频率分辨率的改善,图10中的第31个距离单元的聚焦效果被选取出显示于图11。图11(a)为STFT算法对方位向的聚焦效果,图11(b)为本文所提方法对方位向聚焦的效果,由图可见,该距离单元主要包含两个散射点,此处选择第一个峰值(图11(a)中X=119,图11(b)中X=56)用比较频谱宽度,具体谱峰宽度数据如表3所示。可见,所提成像方法的峰值的下降速度比STFT算法的峰值下降速度快,即图11(b)中的峰值宽度更窄,即所提方法能获得更好的方位向聚焦效果。 上述实验结果已经证实基于联合时频分析和谱估计的成像方法的有效性,更进一步的机动目标ISAR超分辨成像算法的研究将在未来的工作呈现。 (a) STFT算法聚焦效果 (b) 所提方法聚焦效果图11 波音B727实测数据第31个距离单元的聚焦效果 表3 实测数据第一个谱峰的宽度 本文介绍了一种联合时频分析和谱估计的机动目标ISAR成像算法,该方法在整个成像时间内选取一段短时间对目标进行方位向压缩,进而克服长时间内的多普勒频率的时变特性,然后应用MUSIC谱估计方法对上述方位向压缩结果进行超分辨处理,最终在该段短时间内实现机动目标的高分辨成像。相比于单一的时频分析方法,所提方法可以克服“不确定”原则对成像分辨率的限制,获得高分辨成像结果。最后,通过仿真模型和波音B727实测数据证实了所提方法的有效性。


2.3 具体成像步骤



3 ISAR成像实验与分析




3.1 散射点仿真模型实验







3.2 波音B727实测数据实验







4 结束语

