灰色拓扑预测改进及其在热负荷预测中的应用
付万元 马广兴、2 张宁
1 内蒙古工业大学土木工程学院
2 内蒙古自治区土木工程结构与力学重点实验室
3 内蒙古集宁一中
随着我国现代化进程的加快,使得供暖面积以每年2~3%的速度增长[1]。供暖面积的增长使能源消耗急剧上升。因此,有效地降低建筑采暖能耗已经成为了我国节能工作的重中之重[2]。通过跟踪预测用户热负荷的变化,并制定相应运行控制策略是减少热能浪费的有效途径之一[3-4]。灰色拓扑预测模型因具有对样本数据需求少,收敛速度快,精度高以及便于验算的优点已在交通、天文、能源、农业、经济等众多领域得到广泛应用[5-6]。但是笔者发现灰色拓扑预测在应用中还有不足之处。因此笔者对传统灰色拓扑预测做出了改进,目的是提供一种及时准确的热负荷预测方法,为采暖系统协调运行提供依据。
1 原始数据获取与预处理
本文预测所需的数据有集中供暖系统逐时热负荷及逐时室外温度。具体详细数据来源于呼和浩特市某高校供暖系统。数据采集时间为19/02/01 00:00:00至19/02/13 23:00:00,热负荷值共计312 组,室外温度值共计312 组。这一时间段对应室内温度波动幅度不超过依0.4°C,供热质量较高。因此,采集数据经剔除个别异常值可以用作负荷预测。
1.1 原始数据预处理的重要性
由于预测需要一定量的历史负荷数据,对未来的热负荷进行预测。历史数据的准确与完整程度直接关系到负荷预测的精度,在数据采集过程中由于记录仪器、传输通道、接收仪器等发生故障都可能导致所采集数据异常或缺失。若将异常数据不经处理用于热负荷预测,其中带有伪信息,伪的变化规律必将影响预测结果的准确性,因此,在进行热负荷预测模型的建模前,必须将原始数据中的异常值进行剔除与缺失数据的补全处理以还原热负荷序列中隐藏得正确信息与规律。
1.2 异常负荷数据的剔除
文中采用的异常数据剔除方法为数据横向比较法,设Q(t)为第t 时刻的热负荷数据;Q(t-1) 为第t-1时刻热负荷的数据;Q(t+1)为t+1 时刻热负荷的数据;将t-1 时刻热负荷的数据和t+1 时刻热负荷的数据的平均值与t 时刻的热负荷数据Q(t)做比较,若所得比值大于或小于所设定的阈值,则视该点数据为异常值,将其剔除。计算公式如下:
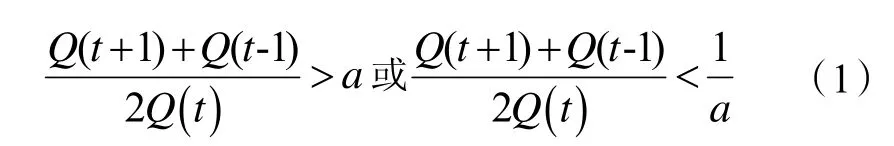
式中:a 为给定的阈值。
通过以上变化,可以将负荷序列中的假数据、伪数据剔除。保留负荷序列中大部分的有效数据。并采用异常和空缺值的时刻点前一时刻和后一时刻的负荷平均值替换异常和空缺值得负荷数据。
针对本文19/02/01 00:00:00 至19/02/13 23:00:00所采集数据,阈值a 设定为1.2。然后计算某一时刻相邻时间点对应负荷平均值与该点负荷值的比值,将计算结果与所给定的阈值相比较,判定异常值并剔除,用前后点负荷数据之间的平均数代替,具体处理结果见图1。
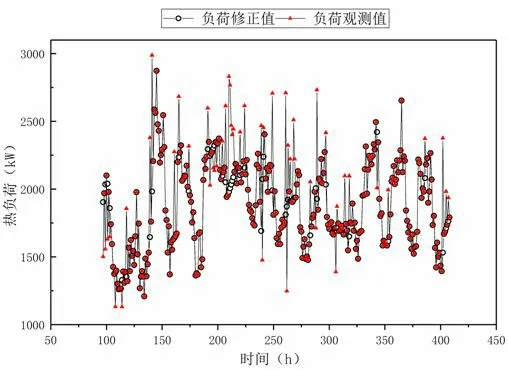
图1 处理数据与原始数据对比
将时间设定为1~312 h,对应负荷处理结果记为Qi(i=1,2,…,312)。
2 模型建立
2.1 数据标准化及归一化
传统灰色拓扑预测在应用中只是通过历史样本数据建立模型来寻找样本的整体规律,未涉及影响结果的其他因素,致使预测值与实际值存在较大偏差。本文加入了影响未来负荷的主要因素——室外温度这一数据来降低预测值与实际值得偏差。
模型所用数据存在单位和量级都不同的现象。因此,应将数据进行标准化处理。数据的标准化,是指将数据进行比例缩放处理,使之落入一个特定区间。数据的标准化处理能够去除数据的单位限制,将数据处理转化为无量纲参数,便于不同单位或量级的数据能够进行比较和加权。本文选择的样本数据处理方法是数据标准化的典型形式,即数据的归一化处理,将数据统一映射到[0,1]区间上。

式中:XI为归一化目标值;Xi为输入样本数据;Xmax、Xmin为输入样本数据的最大值和最小值。
2.2 灰色拓扑预测
2.2.1 基于分数阶序列的灰色拓扑预测
将待分析的数据资料做成曲线图,根据研究的需要选取一组阈值,在曲线图上分别寻找与各阈值线的交点,交点在横坐标的投影到原点的距离作为该阈值GM(1,1)建模的原始数据,用这些时刻数据分别组建GM(1,1)模型,每个阈值对应一个GM(1,1)模型,用该模型群预测每一阈值未来可能出现的时间,将这些预测时间值和对应的阈值组成的点连接起来,得到的曲线就是灰色拓扑预测的未来波形变化趋势图。研究表明,分数阶算子GM (1,1) 模型的模拟精度高于传统GM(1,1)模型,具有更强的普遍适用性[7]。因此,灰色拓扑预测中阈值对应GM(1,1)模型以分数阶累加序列和分数阶累减序列建模区别于传统GM(1,1)模型以一阶累加序列和一阶累减序列建模。
2.2.2 对预测序列还原
预测所得结果为落在区间[0,1]的数值,设所得序列为qi(i=97、98、…、120),需要经过还原得到预测负荷值。还原式为:
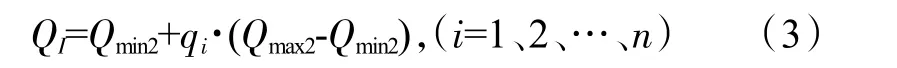
Qmax2、Qmin2确定如下介绍:
建筑物供暖热负荷计算公式Q=q·V·(Tn-Tw),其中Q、q、V、Tn、Tw分别是建筑供暖热负荷、建筑物的体积供暖热指标、建筑物的外部体积、供暖室内计算温度、供暖室外温度。q、V、Tw在整个供暖过程中为定值,Q随着室内外温差Tn-Tw的变化而变化,记Tn-Tw为吟T。将采集数据时间设定为1~312,对应室内外温差值为吟Ti。
找出室内外温差序列(吟Tj+1、吟Tj+2、…、吟Tj+23、吟Tj+24)(j=1、2、…、n)共24 组数据中的最大值和最小值,记为吟Tmax1、吟Tmin1;找出室内外温差序列(吟Tj+25、吟Tj+26、…、吟Tj+47、吟Tj+48)(说明:吟Tj+25、吟Tj+26、…、吟Tj+47、吟Tj+48作为预测前馈信息,在实际运用中可通过设定室内温度值与中国气象网获得未来24 小时逐时温度值做差得到)共24 组数据中的最大值和最小值,记为吟Tmax2、吟Tmin2。
室内外温差序列(吟Tj+1、吟Tj+2、…、吟Tj+47、吟Tj+48)共48 组数据按照下式进行标准化处理:
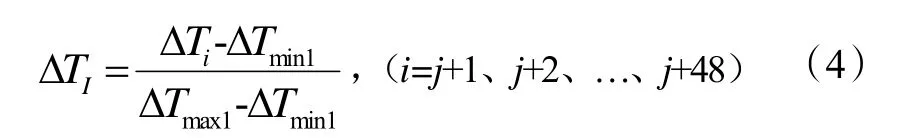
得到室外温度值标准化处理得到序列(吟tj+1、吟tj+2、…、吟tj+47、吟tj+48),在序列(吟tj+1、吟tj+2、…、吟tj+23、吟tj+24)中的最大值和最小值分别为1 和0,在序列(吟tj+25、吟tj+26、…、吟tj+47、吟tj+48)最大值和最小值分别是。
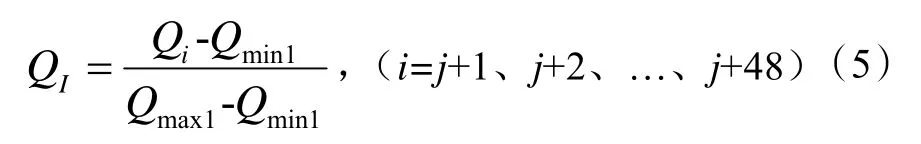
得到室外温度值标准化处理序列(qj+1、qj+2、…、qj+47、qj+48),在序列中(qj+1、qj+2、…、qj+23、qj+24)中的最大值和最小值分别为1 和0,在序列(qj+25、qj+26、…、qj+47、qj+48)最大值和最小值分别是(Qmax2-Qmin1)/(Qmax1-Qmin1)和。

3 预测过程
将热负荷值序列(Q1、Q2、…、Q24)、(Q25、Q26、…、Q48)、(Q49、Q50、…、Q72)、(Q73、Q74、…、Q96)分别归一化,得到热负荷值归一化序列(q1、q2、…、q24)、(q25、q26、…、q48)、(q49、q50、…、q72)、(q73、q74、…、q96);再将未来24 小时室内外温差序列(吟T97、吟T98、…、吟T120)归一化,得到室外温度值归一化序列(吟t97、吟t98、…、吟t120);将室外温度值归一化序列(吟t97、吟t98、…、吟t120)分别与热负荷值归一化序列(q1、q2、…、q24)、(q25、q26、…、q48)、(q49、q50、…、q72)、(q73、q74、…、q96)加权相加;得建模序列:(a·吟t97+b·q1、a·吟t98+b·q2、…、a·吟t120+b·q24)、(a·吟t97+b·q25、a·吟t98+b·q26、…、a·吟t120+b·q48)、(a·吟t97+b·q49、a·吟t98+b·q50、…、a·吟t120+b·q72)、(a·吟t97+b·q73、a·吟t98+b·q74、…、a·吟t120+b·q96)。
将上述序列分别归一化得到序列(q10、q20、…、q240)、(q250、q260、…、q480)、(q480、q490、…、q720)、(q730、q740、…、q960)。
3.1 绘制二维平面关系曲线
将上述值为纵轴,时间为横轴,建立二维平面关系曲线,在曲线上取一系列阈值εi,阈值的选择能够反映波形的发展变化和控制波形的幅度。由阈值做一系列平行于横轴的平行线,得出相对应的交点横坐标值,即阈值对应的时间点序列。以阈值对应的时间点序列为数据,建立GM(1,1)模型群,根据模型对未来24 小时负荷值进行预测。
3.2 基于分数阶序列的GM(1,1)模型建立
1)计算X(0)的r 阶累加生成序列X(r)
r 阶累加生成算子公式为:

其中:祝(n)=(n-1)!
2)对x(r)作紧邻均值生成序列Z(r)

3)计算的X(r)一阶累减生成序列X(r-1)
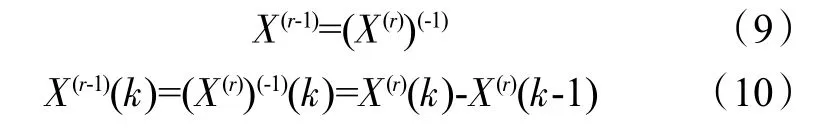
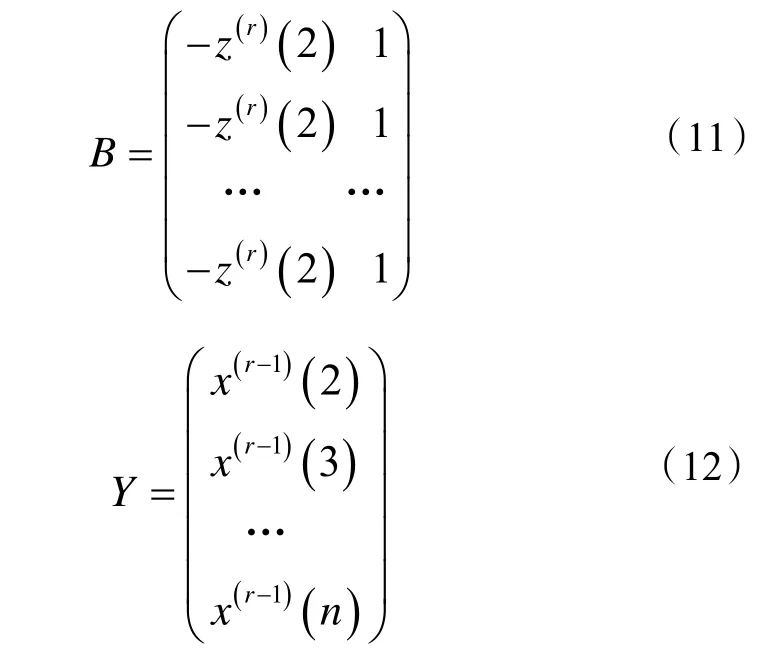
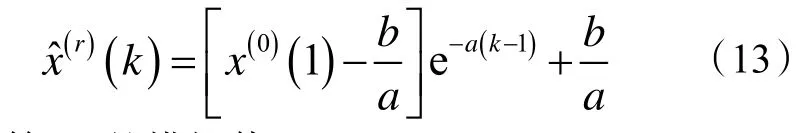
6)计算X(r)的模拟值
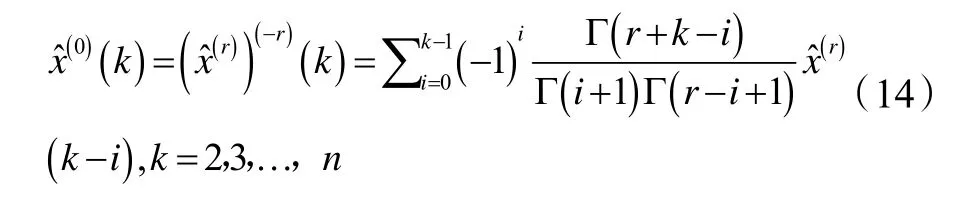
3.3 绘制灰色拓扑预测曲线
通过模型GM(1,1)群得到的预测结果按照时间出现的先后顺序画在相应的坐标上,并将这些点以光滑曲线连接,记为灰色拓扑预测模型的预测曲线,上述作图在origin 中完成,通过纵向坐标读取器,可读取未来24 小时某一时刻的负荷值。得到未来24 小时热负荷值归一化序列(q97、q98、…、q120)。
3.4 灰色拓扑预测序列还原及再利用
将得到的未来24 小时热负荷值归一化序列(q97、q98、…、q120)还原,还原式为式(3)。将还原值(Q97、Q98、…、Q120)作为新信息置入预测序列,去掉原预测序列的老信息(Q1、Q2、…、Q24),用序列(Q97、Q98、…、Q120)建模,预测下一天负荷值(Q121、Q122、…、Q144)。以此循环,得到Q144后续负荷值。
3.5 误差检验
对连续预测得到的负荷值按照式(15)~(17)进行误差分析:
残差检验公式
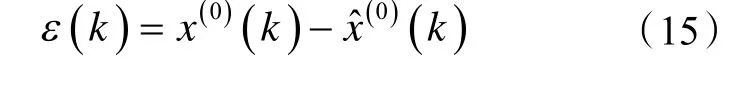
相对误差检验公式

平均相对误差检验公式
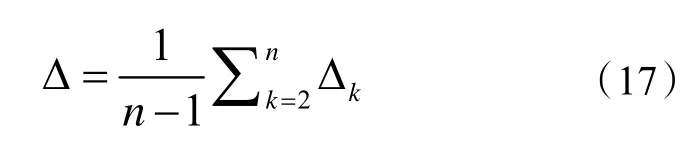
4 实例应用
4.1 给定阈值求取时间序列
阈值的选择能够反映波形的控制波形的摆动幅度和发展变化,根据选择阈值的原则,将阈值数据进行划分即ξ1=0,ξ2=0.2,ξ3=0.35,ξ4=0.51,ξ5=0.7,ξ6=0.85,ξ7=1,将上述阈值做平行于横轴的直线,得出与原始数据交点,得出若干组不同阈值的时间序列(图2)。

图2 阈值划分图
将所得时间序列置于表1(由于连续热负荷呈周期性波动,波动周期T 为24依2,因此将同一阈值下得的时间序列按照周期T进行分类):

表1 时刻序列表
4.2 建立基于分数阶序列的GM(1,1)模型
以阈值1 对应序列(7.18,27.12,56.09,80.06)具体为例:
1)对该序列进行r 阶累加处理,r=-0.2 可得到序列(7.18,25.684,50.0916,66.32776)
2)对x(r)作紧邻均值生成序列Z(r),得到序列(16.432,37.8878,58.20968)
3)计算的X(r)一阶累减生成序列X(r-1),得到序列(18.504,24.4076,16.23616)
重复上述步骤,得到不同阈值对应灰色预测模型,并将结果置于表2:

表2 预测时间响应式
4.3 绘制灰色拓扑预测曲线
通过模型GM(1,1)群得到的预测结果按照时间出现的先后顺序画在相应的坐标上,并将这些点以光滑曲线连接,记为灰色拓扑预测模型的预测曲线,上述作图在origin 中完成,通过纵向坐标读取器,可读取未来24 小时某一时刻的负荷值(图3)。
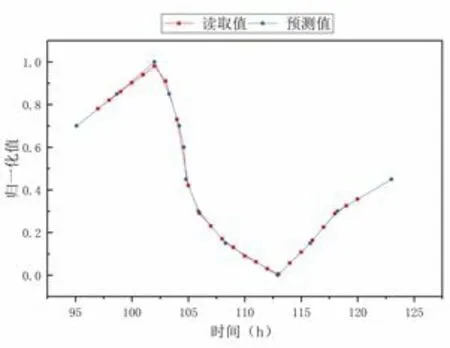
图3 灰色拓扑预测图
4.4 灰色拓扑预测序列还原及再利用
确定该区间最大值及最小值,在此例中Qmax1,Qmin1,吟Tmax1,吟Tmin1,吟Tmax2,吟Tmin2为2264.8,1384.25,31.95,18.45,29.5,10.45,QI=吟ti(Qmax-Qmin)+Qmin=2105,QJ=吟tj(Qmax-Qmin)+Qmin=1253.9,将预测数列(q97、q98、…、q120)按照式(3)进行还原,并将还原所得值用作为信息用到下一天预测建模中。最终将19/02/05 00:00:00 至19/02/13 23:00:00 负荷预测值与真实负荷值整理具体如图4。

图4 真实值与预测值对比
对19/02/05 00:00:00 至19/02/13 23:00:00 负荷预测值与真实负荷值共计216 组对比数据作误差分析,平均相对误差为9.294%。
5 结论与展望
文章对灰色拓扑预测在热负荷预测应用中的不足提出了一种改进方法:传统灰色拓扑预测在应用中只是通过历史样本数据建立模型来寻找样本的整体规律,未涉及影响结果的其他因素,本文加入了影响未来负荷的主要因素——室外温度。灰色拓扑预测中阈值对应GM(1,1)模型以分数阶累加序列和分数阶累减序列建模区别于传统GM(1,1)模型以一阶累加序列和一阶累减序列建模。预测所得结果为落在区间[0,1]的数值,根据供暖相关知识得出了预测数列还原为负荷值的数学关系式,还原式为(6)。
以采暖系统中未来热负荷实时预测为例,改进方法成功对某高校集中供热系统热负荷的未来值进行了全波形预测,对未来负荷预测值与真实负荷值共计216 组对比数据作误差分析,平均相对误差为9.294%,验证了该模型在热负荷呈现波动性时具有精度高、可靠度高的特点。本文所讲述的方法可以作为采暖系统实现“按需供热”,保障热用户舒适性的基础和前提。

