一种关于巴哈车架的建模和仿真

陈博文

（211167 江苏省 南京市 南京工程学院）

0 引言

车架是汽车的骨架，通常用于支撑和连接汽车各个零部件；不仅要承受来自各个方向的载荷，同时还要保护车手的安全。在巴哈赛车中，车架除了用于支撑所有其他功能的系统之外，还同时兼具有防滚架的作用，增强车身总体强度、抗扭弯度等，在车体发生侧翻时保护车手不受伤害，减少地面带给车手直接的冲击。

本文以巴哈车架为研究对象，参照2020 巴哈大赛竞赛规则，采用正向设计的方案，利用有限元分析软件对车架强度（包括静态载荷、弯曲工况、制动工况、转弯工况）、车架刚度（包括扭转刚度、弯曲刚度）、自由模态的有限元仿真分析。基于软件仿真结果得出各个工况下的应变、位移、支反力云图，计算车架扭转、弯曲刚度来评判车架的合理性，实现巴哈车架的建模和仿真。

1 巴哈车架材料与管件参数的确定

参照2020 巴哈大赛竞赛规则中对车架材料和尺寸规格的要求：拟采用4130 合金钢（30CrMo）为管件基准钢铁材料，其力学性能远比Q235钢高，屈服强度可达785 MPa，抗拉强度超过985 MPa；具有很高的强度和韧性；材料的基本参数：密度为7 850 kg/m3，泊松比约为0.279，杨氏模量为2.11E+11 Pa。根据2020 巴哈大赛要求，拟决定车架主要管件规格Φ25.4 mm×3.0 mm,次要管件规格Φ25.4 mm×1.7 mm[1]。

在CATIA 里先确定好杆件连接点、悬架硬点等位置的参数，初步画出车架的空间线图（如图1 所示）。完成线图后，再对线图拔肋，分别对主要管件和次要管件按不同规格起肋管，注意在多个杆件连接处需要对该段做坡口处理，运用布尔切割把干涉段减去，保留主要杆件，避免计算时重复计算重合段质量。部分管件需要弯曲处理，弯管延伸段不得超过838 mm，且弯径必须小于152 mm。除非添加扣板加固车架防滚环与防滚箍之间的连接，其规格参数同主要管件一致，车架总质量约为41.457 kg，初步设计的巴哈车架钢管图为如图2 所示。

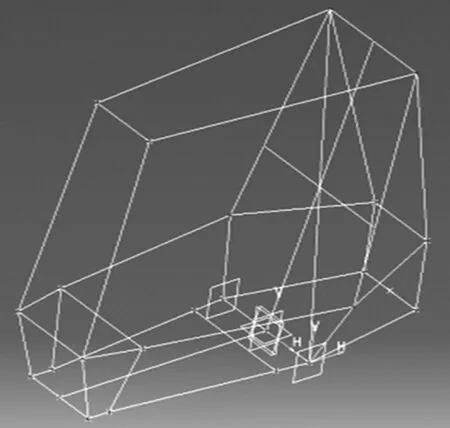
图1 巴哈车架空间线图Fig.1 Baja frame line diagram

图2 巴哈车架钢管图Fig.2 Baja frame steel pipe diagram

2 巴哈车架有限元仿真分析

将CATIA 保存的STP 模型导入到Workbench中，利用static structural（静态结构）板块完成静态载荷、刚度分析、自由模态等多个有限元仿真。

初步设定有限元模型建立时网格尺寸为10 mm，共有5 615 个节点和2 812 个梁单元。钢管连接方式采用焊接，保证相邻钢管之间节点重合，使得所有管件成为一个整体，如图3 所示。

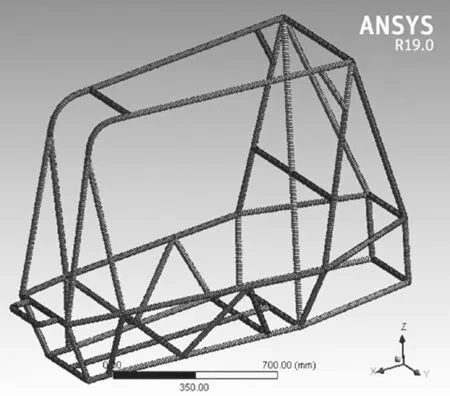
图3 车架网格划分Fig.3 Meshed frame

2.1 静态载荷分析

车架所受静态载荷包括车架自身重量、驾驶员体重、发动机、转向系统等，在Workbench 中，通过简化为添加重力场、集中载荷、均布载荷来达到加载静态载荷的目的。由于车架在行驶过程中会受到动载、偏载、冲击载荷等多种载荷类型综合作用，考虑到车架的载荷类型多样化，且为理想化模型，存在其他单元分担车架所承受的载荷，因此需要进一步计算。设车架所受载荷公式为

式中：FS——等效载荷；m ——质量；g ——重力加速度，取9.8 N/m2；AS——等效载荷系数，计算载荷时取2.0～2.5，这里取2.5[2]。

可得车架所受静态载荷情况如表1 所示。

表1 车架所受静态载荷情况Tab.1 Static load conditions on the frame

图4 为车架在静态载荷状态下整体应力分布以及添加的悬架约束条件。

图4 静态载荷下车架所受约束条件Fig.4 Constraints under static load

2.2 车架强度分析

2.2.1 弯曲工况分析

为模拟车架在静止状态下应力分布并分析车架弯曲变形情况，以重力场、均布载荷、集中载荷等多种形式对车架进行仿真，检验其强度、抗疲劳能力。同样，计算载荷时需要乘以一个等效载荷系数，通过对车架与悬架的连接点添加约束，将载荷添加到车架，实现车架弯曲工况的模拟[3]。

弯曲工况分析时，车架具体约束方式添加如表2 所示。

表2 弯曲工况下车架约束方式Tab.2 Frame constraints of bending conditions

经过有限元分析，车架在弯曲工况下的应力云图如图5 所示，最高可达2.747 6 mm；应力分布云图如图6 所示，最大应力为31.277 MPa，出现在防滚箍和防滚环连接处，此处多管件连接，易出现应力集中现象。远低于4130 钢的屈服极限785 MPa，所以车架整体存在很大的强度富余量，存在很多优化空间.

图5 弯曲工况下的应力云图Fig.5 Stress nephogram under bending condition

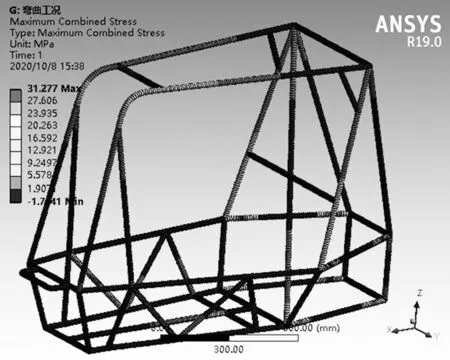
图6 弯曲工况下的应力分布云图Fig.6 Stress distribution nephogram under bending condition

2.2.2 制动工况分析

为模拟车架在比赛中遇紧急制动时所受载荷情况，赛车在制动时会受到一个纵向的惯性力作用。惯性力的大小由赛车和车手总体质量的大小、制动减速度决定。通过对车架施加1.4g 的制动减速度，并约束车架各个悬架硬点的自由度来实现制动工况的分析。

制动工况分析时，车架具体约束方式添加如表3 所示。

表3 制动工况下车架约束方式Tab.3 The frame constraints of braking conditions

图7 所示为制动工况下车架的位移云图，最大可达3.646 4 mm；图8 所示为制动工况下车架的应力云图，最高可达44.892 MPa，主要集中在后悬架硬点区域和防滚环焊点。

图7 制动工况下的位移云图Fig.7 Displacement cloud diagram under braking condition

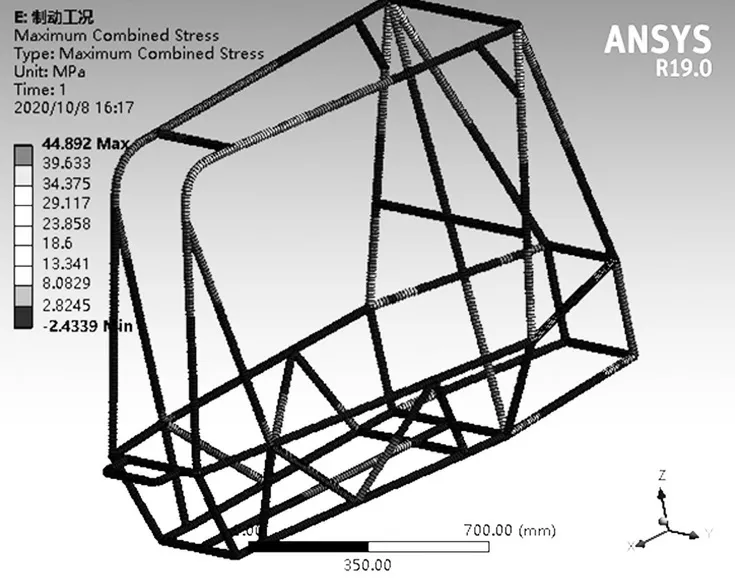
图8 制动工况下的应力云图Fig.8 Stress nephogram under braking condition

2.2.3 转弯工况分析

行驶过程中，车架会因为转向时的离心力作用受到横向载荷，会对车架产生一个弯曲变形的作用。同时，当赛车经过坑洼路面时，产生轮跳会对车架有扭曲变形的作用。通过对车架加载离心加速度和对其悬架硬点约束来达到模拟转弯工况分析。

转弯工况分析时，车架具体约束方式添加如表4 所示。

表4 转弯工况下车架约束方式Tab.4 Frame constraints of turning conditions

图9 所示为车架在转弯工况下的位移云图，其最大位移量为4.658 9 mm 在防滚箍和主环连接处；图10 所示为车架在转弯工况下的应力分布云图，最高可达45.287 MPa，主要集中在后悬架硬点处附近。

图9 转弯工况下的位移云图Fig.9 Displacement cloud map under turning condition

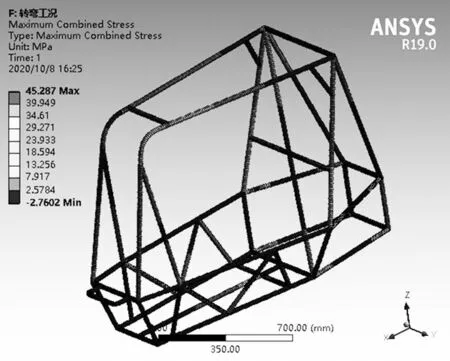
图10 转弯工况下的应力分布云图Fig.10 Stress distribution nephogram under turning condition

2.3 车架刚度分析

2.3.1 扭转刚度分析

将车架看作简支梁，通过给车架上的左前悬架硬点和右前悬架硬点处添加相反方向的位移约束，后悬架硬点均限制方向移动，释放所有硬点的旋转自由度，以达到对车架实现扭转效果。

扭转刚度分析时，车架具体约束方式添加如表5 所示。

表5 扭转刚度时车架约束方式Tab.5 Frame constraints of torsion stiffness

考虑到对整车扭转刚度分析时的扭转角度小，可利用扭转刚度计算公式

式中：M——转矩；θ——扭转角度；F——支反力；l——位移约束的横向距离；h——位移约束竖直距离。

经过有限元分析可得，在使前悬架产生1 mm 扭转所需支反力为F=3 426.9 N，位移约束的横向距离l=0.42 m，位移约束竖直距离h=0.02 m。解出扭转刚度Sr=5 330.7 N·m/(°)，而一般巴哈车架扭转刚度应大于1 000 N·m/(°)，符合设计所需要求。

其应力分布云图如图11 所示。可以看出，车架整体应力较低，最大应力为289.05 MPa，主要分布在前横梁和防侧撞结构件的连接处，此处为多个管件连接接口处，易产生应力集中现象，加上扭转刚度分析时给车架一定的强制位移会产生较大应力。而4130 钢材料的屈服极限为785 MPa，最大应力小于屈服极限，故检验合格[4]。

图11 扭转应力分布云图Fig.11 Torsional stress distribution nephogram

其位移云图如图12 所示。最大位移分布在防滚箍和防滚环连接处，约为3.081 4 mm。

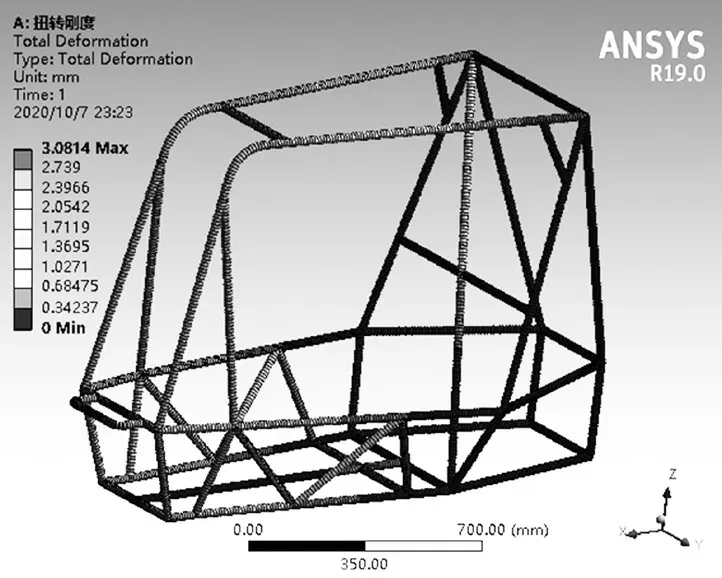
图12 扭转位移云图Fig.12 Torsional displacement cloud map

2.3.2 弯曲刚度分析

将车架视作简支梁，前悬架和后悬架的连接点作为支点，仅释放左右前悬架Y 方向的自由度。

对车架中部区域加载压力，最后检测其弯曲变形程度和应力分布情况。车架具体约束方式添加如表6 所示。

表6 弯曲刚度时车架约束方式Tab.6 Frame constraint mode for bending stiffness

计算简支梁的弯曲刚度：

式中：F——施加的载荷；l——前后悬架硬点距离；a——施加载荷的点到前悬架硬点的距离；b——施加载荷的点到后悬架硬点的距离；w——车架底部挠度。

拟在车架中部施加一个F=5 000 N 的载荷，前后悬架硬点l=1.200 2 m，前悬架应点到施加载荷点的距离a=0.707 5，后悬架应点到施加载荷点的距离b=0.492 7。由应力云图标尺可得挠度w=0.81×10-3m（如图13 所示）。将数值代入式（3）可得弯曲刚度：EI=207 642 N·m2，符合弯曲刚度要求[5]。

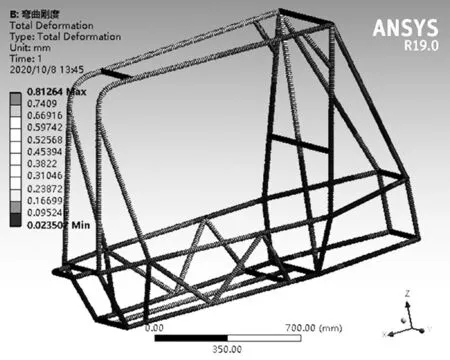
图13 抗弯刚度作用下位移Fig.13 Displacement under bending stiffness

2.4 自由模态分析

行驶过程中，由于路面颠簸，会对车架产生激发振动，发动机工作时自身又会产生震动。当两种震动频率相同时会出现共振现象，从而对车架造成较大的损害。利用Workbench 中的模态分析板块，对车架进行自由模态分析，即采用自由边界的方法，不添加任何的外部载荷和约束对车架分析。

赛车行驶过程中，两个主要的激振源由来分别是路面激励和发动机激振。巴哈赛车选用的发动机是Briggs &Stratton 10 HP OHV Vanguard 19的未经改装单缸四循环风冷发动机，怠速状态下发动机转速约为1 750 r/min，最高转速状态下约为3 600 r/min。参考发动机激励频率公式，分析发动机振动的频率范围。

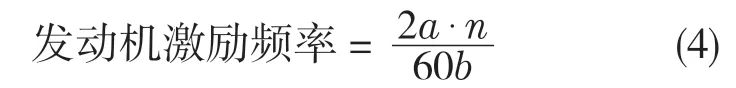
式中：a——发动机的缸数；n——发动机的转速，r/min；b ——发动机冲程数。

由式（4）得发动机激励频率为14.58～30 Hz，相较于车架自由模态分析频率，由于前6 阶为刚体模态，频率几乎为0，到第7阶时出现了车架的固有频率。理论上，车架的前几阶频率是最容易激发出来的，随震动阶次的提高，模态越难以被激发出来[6]。

经过自由模态分析可得，车架总体震动频率均高于发动机激励频率，不会引起共振现象。

3 结论

本文以2020 巴哈大赛竞赛规则为基本，详细阐述了巴哈车架在CATIA、ANSYS 中的建模分析方法，并对车架进行有限元静力学分析。仿真结果表明：该车架在各种工况下都能基本满足强度和刚度要求。综合弯曲工况、制动工况、转弯工况三大工况下的车架应力分布情况可知：应力主要集中在发动机舱的后悬架硬点处，且管件连接点可能会出现应力集中现象，加剧管件的变形，需对目标管件进行加固处理；从扭转刚度、弯曲刚度的分析结果可知：车架整体结构仍有一定优化空间，仍有一定的刚度富裕量，整体架构还可进一步实现空间拓扑优化,适当减小次要管件的尺寸使得整车车架实现轻量化，从而降低车架的整体质量。