基于NFTSMC 的开关磁阻电机预测转矩控制系统

严紫光，邵飞旋

（200093 上海市 上海理工大学 机械工程学院）

0 引言

开关磁阻电机（SRM）具有低速高转矩、结构简单稳定、转子无绕组和永磁体、高容错性等优点，因此成为了混合动力汽车中最常用的电机类型之一，目前主要用于商用车[1]。然而，SRM具有独特的双凸极结构，它在运行时出现的磁链饱和、涡流损耗和磁滞效应等因素使得它呈现出严重的非线性特性，尤其在低速运行时会出现较大的转矩脉动[2]，限制了其在乘用车上的应用效果，因此对SRM 转矩脉动的抑制一直是国内外学者研究的热点。

近年来，预测转矩控制（PTC）已经成为一种适用于非线性和多变量应用的新颖方案。文献[3-4]利用分析方法对SRM 的磁链曲线进行拟合以提高预测模型的精确度；文献[5]提出了一种基于十二扇区电压矢量选择的预测控制方法。文献[6]基于直接转矩控制中扇区划分的方法推导出了新的开关状态切换表以减少预测电压矢量的数量，并设计了多目标成本函数以同时考虑转矩脉动、铜损和平均开关频率；文献[7]提出一种在线自适应调整SRM 的关断角，以避免由于有限控制模型预测控制（FCS-MPC）需要足够长的预测范围而导致电感下降区域中的电流产生负转矩；文献[8]通过将转矩分配函数（TSF）与PTC相结合来减少转矩脉动；文献[9]设计了一种新型TSF 以补偿输入相转矩供应能力的不足。文献[10-11]为了解决SRM 转矩脉动大的问题，提出一种基于模型预测磁通量控制的直接转矩控制方法。

以上提到的控制方法大多只是对转矩或是磁链的单一控制，并且当成本函数中包含多个变量时很难确定各变量的权重系数。本文对开关磁阻电机的预测转矩控制策略进行优化，加入延时补偿，设计单目标成本函数，并且在速度环采用非奇异快速终端滑模控制代替传统PI 控制。通过仿真验证，该方法使得系统能够较好地抵抗负载扰动并减小转矩脉动。

1 开关磁阻电机基本方程与非线性模型

1.1 SRM 基本方程

考虑绕组电阻压降，忽略磁饱和以及相电流对电感的影响，可得SRM 第k 相的电压为

式中：Uk，Rk，ik，ψ，L——绕组端电压、电阻、电流、磁链和电感；ω——转子角速度。

根据动力学定律可列出电机转子的机械运动方程

式中：J——转动惯量；m——相数；Tk——第k相的电磁转矩；TL——负载转矩；D——阻尼系数。

忽略绕组间互感，根据虚位移原理，可以得到SRM 在任意运行点α处的单相瞬时转矩

式（1）—式（3）构成了SRM 的基本方程。针对不同的研究目的，可以提出一些假设以对SRM 数学模型进行合理的简化。根据对磁链或非线性相电感近似处理方法的不同，SRM 数学模型可分为线性模型、准线性模型和非线性模型[12]。

1.2 SRM 非线性模型

为了获得较为精确的电机模型以贴合实际运行时的情况，本文通过ANSYS Maxwell 软件对一台额定功率为1.2 kW、额定电压为72 V、额定电流为27 A 以及额定转速为2 000 r/m 的12/8 极式开关磁阻电机进行有限元仿真，其相关参数如表1 所示。经拟合得到SRM 的静态特性曲线，如图1、图2 所示。

图1 静态转矩特性曲线Fig.1 Static characteristic curves of torque

图2 静态电感特性曲线Fig.2 Static characteristic curves of inductor

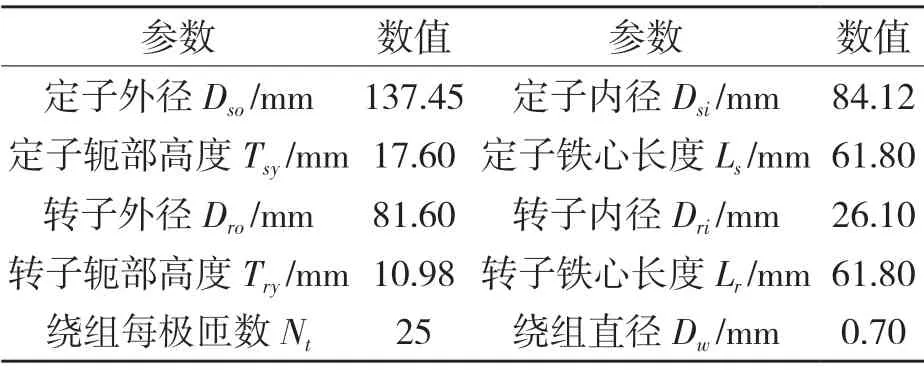
表1 SRM 模型参数Tab.1 Model parameters of switched reluctance motor

本文将SRM 的静态转矩特性与电感特性以查找表的形式导入MATLAB/Simulink 中，构建12/8 三相开关磁阻电机本体模型。

2 开关磁阻电机预测转矩控制策略的优化

2.1 预测转矩控制原理

基于TSF 的预测转矩控制系统框图如图3 所示。采用TSF 将总转矩的期望值Tref分配给每一相，同时完成每一相的换相逻辑判断。根据SRM的状态方程和采样参数，可以从离散预测模型中预测不同开关状态下的输出转矩。通过比较成本函数值可以选出使其获得较小值的开关状态。最终令控制器输出最优的功率电路的状态，以调节各相绕组两端电压值。

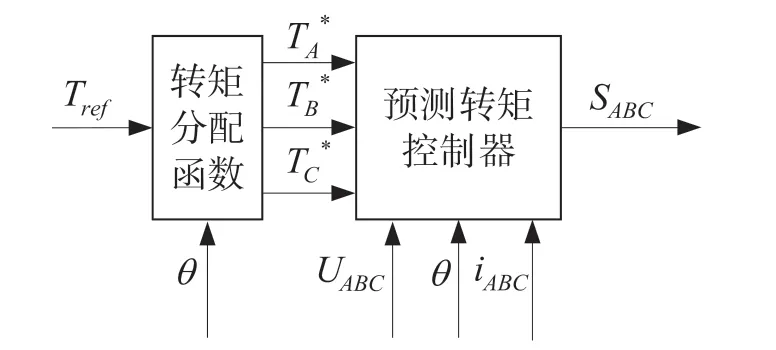
图3 预测转矩控制原理框图Fig.3 Block diagram of predictive torque control principle

2.2 带延时补偿的离散预测模型

将转速方程ω=dθ/dt 代入SRM 的电压方程式（1）中，联立得到微分方程组（4）：

由于采样步长很小，可以将式（4）近似看作线性方程组，因此在一个采样周期内，利用欧拉方程将方程组离散化，得到k+1 时刻的预测电流和转子位置角的离散时间表达式

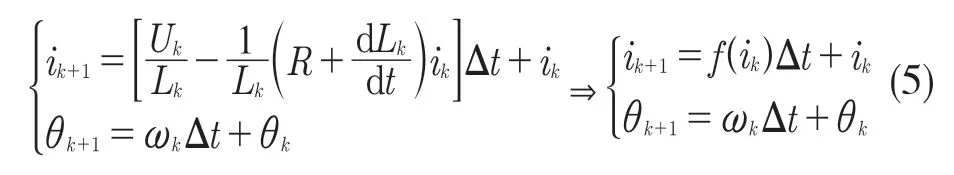
本文采用单步预测控制。考虑到计算的复杂性以及所需的计算时间，系统对k+1 时刻转矩值的预测可能会滞后于k+1 时刻的开关动作，另外由于k+1 时刻的开关状态会影响功率变换器的输出电压，k+2 时刻的电机输出转矩将会受到影响。因此，本文对预测转矩控制器进行延时补偿，即在预测k+1 时刻的转矩值的基础上，进一步预测k+2 时刻的转矩值，经过一次迭代得到k+2 时刻的预测方程：

本文采用传统的不对称半桥作为SRM 的功率变换器。在三种不同的开关状态下，由功率变换器施加在SRM 上的实际相电压可以通过式（7）计算：

式中：Udc——母线电压；UI——开关管上的压降；UD——二极管上的压降；UR——SRM 相电阻上压降。

经过延时补偿后的预测转矩步骤如图4所示。

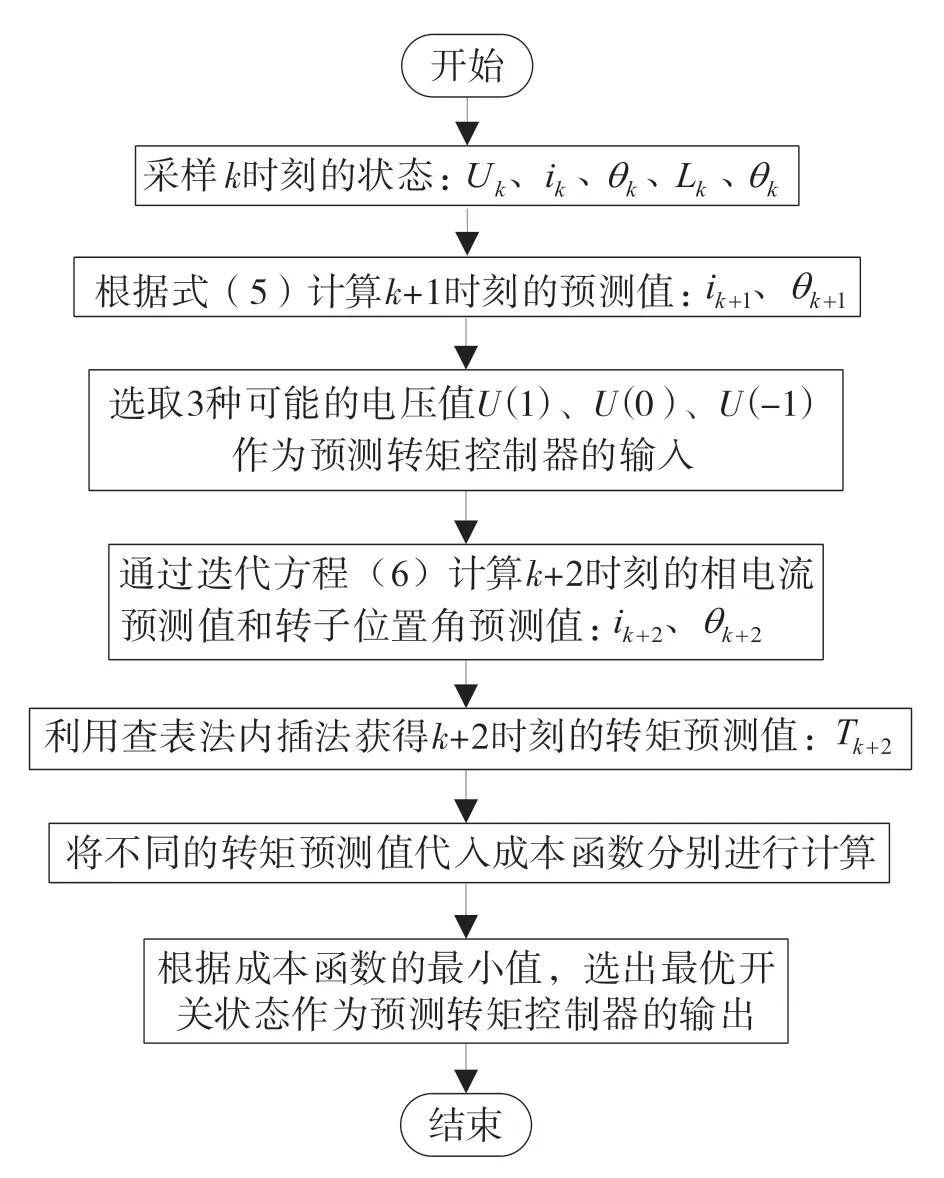
图4 预测转矩控制流程图Fig.4 Flow chart of predictive torque control

2.3 成本函数的设计

文献[13]提出了包含多个控制变量的成本函数，但由于变量的单位不同，很难确定各控制变量的权重系数。为了体现预测转矩控制策略对最小化转矩脉动的优越性，本文不再计及电流的成本函数值，侧重于转矩脉动最小化，成本函数表达式如下：

式中：J ——成本函数；Tref——相期望转矩；Tp——相预测转矩。

以A 相为例，根据开关状态的可能取值，预测转矩候选值为TA（1）、TA（0）或TA（-1），进而得到成本函数候选值为J（1）、J（0）或J（-1）。通过计算 Jmin={J（1），J（0），J（-1）}，若J（1）为其中的较小值，则A 相的最优预测状态为励磁状态。B、C 相情况与A 相类似，不做赘述。

3 非奇异快速终端滑模速度控制器设计

考虑到预测转矩控制对于内部参数变化和外部扰动的敏感性，本文采用滑模控制器代替传统PI 控制器以调节转速。但是，传统滑模控制器存在2 个缺点：一是其具有明显的抖振效应；二是滑模运动难以保证在有限时间内收敛到滑模面。根据文献[14]，利用快速终端滑模控制器可有效解决上述问题。本文在快速终端滑模控制的基础上为避免出现奇异问题，将非奇异快速终端滑模控制器应用到SRM 控制系统中。

SRM 控制系统的状态变量如下：

式中：ωref——给定期望转速；ω——实际转速。

根据式（2）和式（9），状态变量的一阶微分方程可以用矩阵形式表示为

式中：λ=-1/J；u=dTe/dt。

本文将非奇异快速终端滑模面定义为

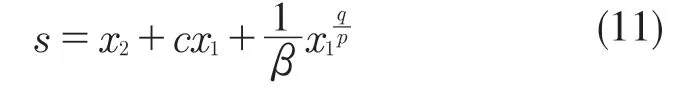
式中：c，β∈R+；q，p ∈N 为正奇数且1＜q/p＜2。

对式（11）求导得

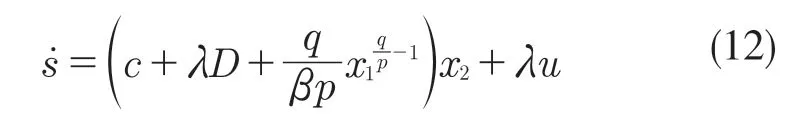
为了保证非奇异性，本文设计了带有终端吸引子的趋近律如式（13）所示：

式中：ξ，γ∈R+；m，n ∈N 为正奇数且0＜n/m＜1。

因此，根据式（12）和式（13），NFTSMC输出的控制量Tref表示如下：

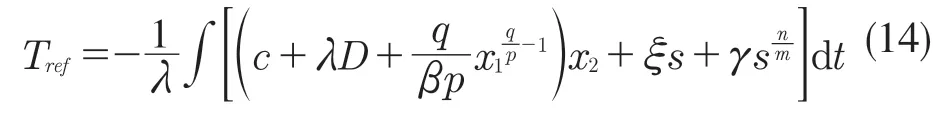
下面对此控制器进行稳定性分析及收敛时间计算。

（1）稳定性分析：

定义Lyapunov 函数为

对式（15）求导得

由于0＜n/m＜1，则1＜n/m+1＜2；又由于m 和n为正奇数，则sn/m+1＞0（s≠0）。由于ξ，γ∈R+，则。因 此，当s ≠0 时，NFTSMC 满足Lyapunov 稳定性条件。

（2）有限收敛时间计算：

令s=0，由式(9)和(11)可得

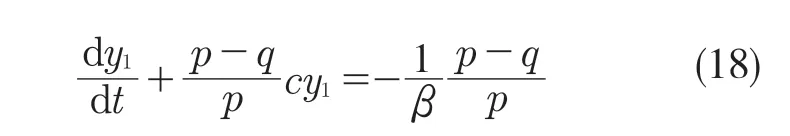
根据一阶线性非齐次微分方程的通解公式，由于t=0 时，C=y1（0），则式（18）的解为

又由于x1=0 时，y1=0，t=ts，则式（19）可写为

化简式（20），可得有限收敛时间为

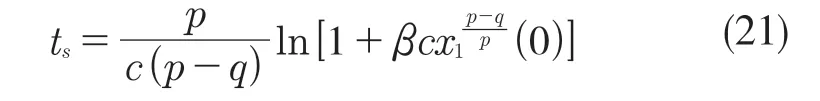
通过设定参数c，β，p，q 可使系统在有限时间ts内到达平衡状态。

引入NFTSMC 的SRM 预测转矩控制系统整体框图如图5 所示。

图5 系统整体框图Fig.5 Overall system diagram

4 仿真验证

为验证本文提出的NFTSMC-PTC 控制方法的可行性与优越性，在不同期望转速和给定负载突变情况下，比较本文控制策略与直接瞬时转矩控制（DITC）方法[15]的控制效果。利用MATLAB/Simulink 仿真软件，搭建SRM 调速系统的仿真模型。

为表征SRM 的转矩脉动，引入转矩脉动系数表达式如下：

式中：Tmax，Tmin——稳态时一周期内的转矩波峰值和波谷值；Tavg——此周期内的平均转矩。

4.1 低速实验

在给定转速500 r/min 下对SRM 控制系统做变负载测试。该系统初始状态为空载运行，在0.06 s时，突加额定负载2 N·m，0.12 s 时，又突减1 N·m的负载。本文控制方法中的NFTSMC 模块的各参数设置为：c=217.8，β=45，p=3，q=5，ξ=0.001，γ=105，m=3，n=1。SRM 控制系统仿真结果如图6、图7 所示。

通过图6 和图7 可知，相比于其他控制方法，在NFTSMC-PTC 控制方法下，电机在启动阶段转速上升最快，能最先达到稳态值，而当电机突加或突减负载时，电机转速存在较小的转速差并能够快速回升至给定值，电机在重新达到稳态后能够保持较低的转矩脉动。由此表明，NFTSMCPTC 控制方法在对抗外部扰动时体现出了良好的鲁棒性。表2 为3 种不同控制方法下的电机动态性能数据对比。其中，ts表示调节时间，Δtr表示加载或减载时的转速恢复时间，kt表示转矩脉动系数。

图6 转速对比图Fig.6 Speed comparison chart

表2 500 r/min 时的系统性能数据对比Tab.2 Comparison of system performance data at 500 r/min

4.2 高速实验

在给定转速1 500 r/min 下对SRM 控制系统做变负载测试，系统负载条件设置与低速实验相同。本文控制方法中的NFTSMC 模块的各参数设置为：c=72.235，β=100，p=3，q=5，ξ=0.001，γ=150 000，m=11，n=5。SRM 控制系统仿真结果如图8、图9 所示。

图8 转速对比图Fig.8 Speed comparison chart

图9 转矩对比图Fig.9 Torque comparison chart

通过图8 和图9 可知，相比于其他控制方法，NFTSMC-PTC 控制方法使得电机在启动阶段有更快的转速响应，能更快达到稳态值，而在电机突加或突减负载时，其转速存在较小的转速差，具有更快的转速回复效果，并能够在重新达到稳态后保持最小的转矩脉动。由此表明，NFTSMCPTC 控制方法具有更快的转速响应，并在对抗外部扰动时体现出了良好的鲁棒性。表3 为3 种不同控制方法下的电机动态性能数据对比。

表3 1 500 r/min 时的系统性能数据对比Tab.3 Comparison of system performance data at 1 500 r/min

5 结论

本文对于SRM 控制系统中转矩脉动的抑制和系统抗扰动的优化提出了一种转速和转矩的联合控制方法。采用带有延时补偿的PTC 对转矩进行控制，同时考虑到PTC 控制方法对于扰动敏感的问题设计了NFTSMC 转速外环进行配合，仿真结果表明所提出的控制方法在有效抑制系统转矩脉动的同时，也能对外部扰动做出快速响应，提高了系统的鲁棒性和稳定性。