柱面气膜密封鼓泡型支承结构力学性能研究
赵超越,刘美红,孙军锋,韦邱发,许冬伟
(650500 云南省 昆明市 昆明理工大学 机电工程学院)
0 引言
目前,柱面气膜密封作为一种新型的、微米级气膜薄膜润滑的非接触式干气密封[1],区别于端面气膜密封独特的柔性支承结构,应用在航空燃气轮中,用来应对其转子系统剧烈振动和热力变形[2],实现密封副之间的非接触,对降低航空燃气轮机油耗损失有一定的重要意义。
柱面气膜密封相比于端面气膜密封的优势在于具有较强的柔性浮动性,允许更大的径向位移,但气膜薄膜一般只有几微米,即使在气膜刚度很大的情况下也无法应对转轴几毫米的径向摆动,所以应合理选用柱面气膜密封的柔性支承结构进行隔离保护,避免密封轴与浮环密封表面因摩擦接触而失效。自从1994 年首次提出柱面气膜密封的概念以来,研究人员尝试了多种柔性支承结构,以柔顺箔、金属橡胶、波箔等比较典型,都取得了一定的成果[3],但也都存在一定的局限性,定量设计难度都比较大,没有推广应用。柔性支承结构在柱面气膜密封中是不可或缺的一部分,对柔性支承材料的选择和结构设计是柱面气膜密封研究亟待解决的问题。本文以箔片动压径向气体轴承作为参考来设计柱面气膜密封新型柔性支承结构。柔性箔片气体轴承常用柔性金属平箔作为内表面,可以采用多种形式底层柔性支承结构为轴承提供一定的形变量[4]。本文采用一种带有鼓泡型箔片的柔性支承结构,探索作为柱面气膜密封柔性支承的可行性。针对鼓泡型箔片动压径向气体轴承,国内外学者先后做了多项研究工作。鼓泡型箔片动压径向气体轴承是由西安交通大学在本世纪初最先提出[5]。侯予[6]等提出了单层鼓泡型箔片轴承并对其进行了理论分析和实验研究,研究表明,此结构有较大的支承刚度和承载能力;卢攀[7]等在不考虑顶层平箔片变形的情况下,分析了单个鼓泡尺寸变化对其支承刚度的影响;赖天伟[8]等提出了采用两层或多层鼓泡箔片作为柔性支承结构,可以有效地调整和改善弹性箔片轴承的刚度和阻尼特性;陈汝刚[9]等提出了以弹性鼓泡支承的新型波箔结构,此结构具有良好的阻尼特性,能够满足微小型高速透平稳定运转。鼓泡箔片动压气体轴承具有优良的性能,自适应性更强,且具有结构简单、制作方便以及适应工作温度的范围广等优点[10],所以本文将其作为参考来设计柱面气膜密封鼓泡型柔性支承结构。
针对鼓泡型柔性箔片这种支承结构,通过仿真分析,获得鼓泡高度、半径以及平箔箔片厚度对其力学性能的影响,得到平箔片和鼓泡箔片的最大等效应力及变形情况,并对结构变形的结果作相应分析。
1 模型参数定义
1.1 模型结构
鼓泡型柔性支承柱面气膜密封结构如图1 所示,主要由转轴、轴套(动环)、浮环(平箔)以及鼓泡箔片等组成。在转轴的转动下,带动轴套同步转动,因轴套外表面开设槽深为10 μm 的T 型槽以及轴套与浮环偏心结构的设计形式,在其间隙处会因流体动压效应形成一层微米级别的气膜薄膜,气膜产生一定的流体动压力使轴套和浮环相互分离。鼓泡箔片置于浮环的外侧,与浮环相接触,用以缓冲转轴因转速过大产生径向位移时动环与浮环发生碰撞。
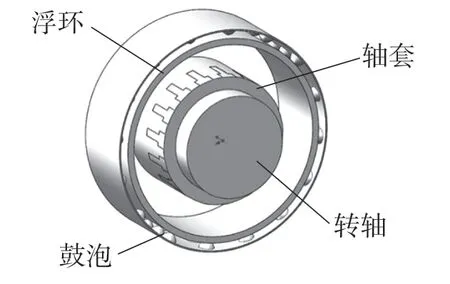
图1 鼓泡型柔性支承柱面气膜密封结构示意图Fig.1 Schematic diagram of bubble-type flexible support cylindrical gas film seal structure
1.2 参数定义
密封介质为空气,本文采用的槽型见图2 所示,具体参数设置见表1 所示。
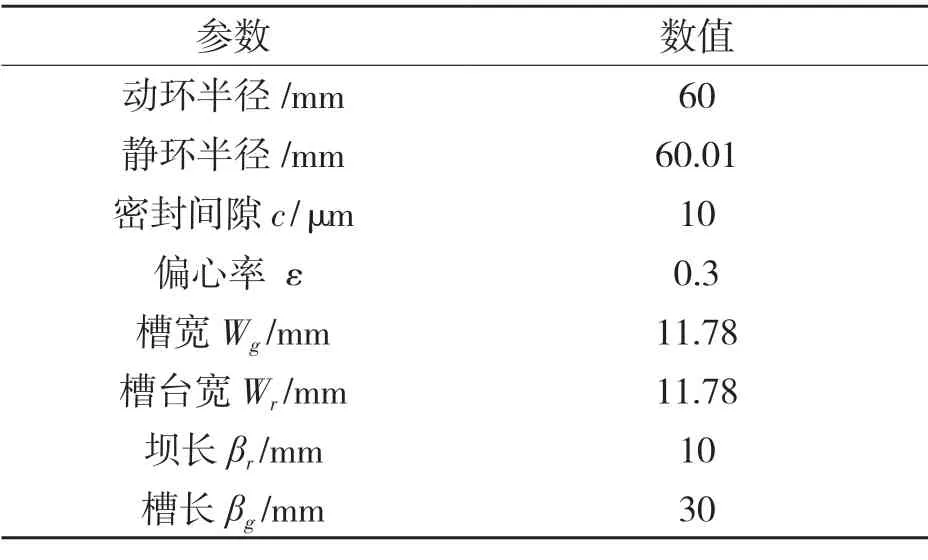
表1 柱面气膜密封结构参数Tab.1 Cylindrical gas film seal structure parameters
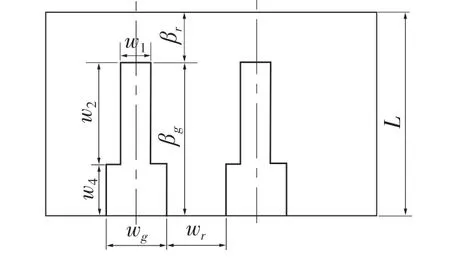
图2 T 型槽柱面气膜展开图Fig.2 The expansion view of T-groove cylindrical gas film seal
本文所采用的槽型为T 型槽,这种槽型在非接触式柱面气膜密封中具有一定的动压效应和正反转工作能力,其槽型结构也是对称布置。
2 流固耦合模型建立
2.1 参数化建模
建立T 型槽柱面气膜密封的动环和静环,其中气膜密封动环外表面开有槽深10 μm 的T 型槽。T 型槽气膜模型如图3 所示,鼓泡模型如图4 所示。
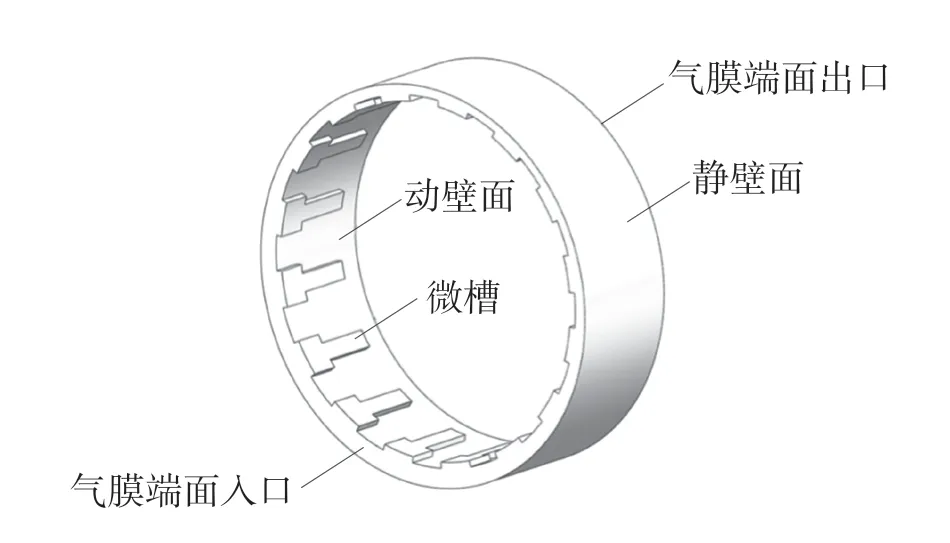
图3 T 型槽气膜模型Fig.3 T-groove gas film model

图4 鼓泡模型的建立Fig.4 Establishment of blister foil model
柔性支承结构主要由3 行16 列相同的鼓泡、鼓泡箔片以及平箔片构成。其鼓泡箔片局部模型示意图如图5 所示,参数设置如表2 所示。

表2 鼓泡型箔片结构参数Tab.2 Structural parameters of bubbling foil

图5 柱面气膜密封鼓泡型柔性支承结构Fig.5 Cylindrical gas film seal bubble type flexible supporting structure
2.2 网格划分
本模型的网格划分需考虑和解决下面几个问题:(1)交界面上的网格和节点的位置非常重要。在计算过程中,画网格的时候,流体交界面和固体交界面网格节点的位置尽量画得相近,保证计算精度。本文采用共型的网格,流体交界面上的网格节点位置和固体交界面上的网格节点位置是一模一样的,提高计算精度;(2)柱面气膜模型横纵尺寸跨度较大,纵向尺寸达到毫米级,而气膜横向尺寸仅有微米级,需要分块进行网格划分。综上,本文采用专业前处理网格划分软件ANSA,分别对流体域和柔性支承固体域进行网格划分。划分后的流体域网格数235 682,固体域网格数572 480,网格类型均是正交性较好的六面体网格。如图6—图8 所示。

图6 T 型槽网格模型Fig.6 Mesh in film of T-groove ring seal

图7 流固共型网格Fig.7 Fluid-solid common mesh
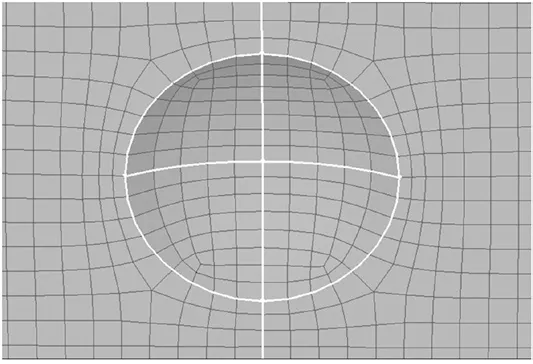
图8 单个鼓泡网格Fig.8 Single bubble mesh
2.3 计算模型假设
(1)假设动环和静环楔形间隙中流体气膜符合牛顿粘性定律的连续介质;
(2)气膜与动环和静环表面无相对滑动,符合无边界滑移条件;
(3)气膜运行稳定,无扰动及振动;
(4)动环和静环在运行过程中无压力变形和热变形;
(5)忽略气膜惯性力和体积力;
(6)只考虑静环的变形与偏转,忽略动环的。
2.4 设置边界条件
(1)流体域内表面:设置旋转速度,模拟轴的转动;
(2)流体域外壁面:这部分是与柔性支承固体接触的FSI 界面,为无滑移壁面条件;
(3)流体域一侧inlet 为端面入口,设置边界条件为压力入口;
(4)流体域另一侧outlet 为端面出口,设置边界条件为压力出口;
(5)平箔内壁面,即与流体域外壁面相重合的一面,设定为流固耦合面;
(6)鼓泡结构与平箔相接触,将鼓泡与平箔接触区设置为接触约束,鼓泡的另一端面设置为固定壁面。
2.5 求解设置
在ANSYS Workbench 平台中,分别建立Fluent 模块和Static Structure 固体模块,将Fluent模块计算压力结果作为载荷加载到固体域计算机几何上。流体分析设置中,采用基于压力求解,选用SIMPLEC 压力修正法来定义分离求解器。
2.6 设定网格独立性检验
如图9 所示,平均气膜厚度为10 μm 的柱面气膜密封浮升力、泄漏量随划分网格数量变化趋势。随着划分网格数量的增加,浮升力、泄漏量都经历了先增大,后趋于平稳的变化趋势。在网格数量从23 万增加到90 万的过程中,气膜浮升力从3 441 N 精确到3 451 N,泄漏量从2.37×10-5kg/s 精确到2.38×10-5kg/s,其运算出来的气膜浮升力误差为0.29%,泄漏量为0.42%。这表明,图9中尽管网格划分更细致,网格数量更多,但其气膜浮升力、泄漏量运算结果误差均小于1%。根据前人的经验[11-12],在不影响流场分析的情况下,网格数量取值尽量小,提高计算效率、减少工作量。综合考虑,采用235 682 的网格数目。

图9 网格无关性验证参数对比图Fig.9 Comparison of grid independence verification parameters
3 单向流固耦合计算结果分析与处理
3.1 气膜流场的分析
转速为12 000 r/min,高压入口侧压力为0.3 MPa,低压出口侧压力为0.1 MPa 时,柱面气膜密封流体域的静压力分布如图10 所示。

图10 柱面气膜密封流体域静压分布Fig.10 Hydrostatic pressure distribution of cylinder gas film seal
动环随转轴进行同步高速转动。因在动环的外表面开设T 型槽,依靠泵吸和动压效应对密封气体进行加压,由于槽区和非槽区之间存在台阶进而在此处引发压降,使得压力在槽根径处积聚,产生较大压力,从而动静环的间隙处形成一层气膜,进行密封。根据静压分布云图,最高压力为0.358 MPa,高压入口侧的压力为0.3 MPa。
3.2 鼓泡结构几何尺寸对柔性支承性能的影响
本节采用控制变量法,针对几个鼓泡结构参数和选用不同材料,分别对单个参数选取不同的数值,分别分析其力学性能。
浮环变形量和等效应力分布如图11、图12所示。可以看出,正是由于鼓泡结构的存在,使得浮环与鼓泡结构的接触端形成了一种柔性接触,使得浮环在接触端产生了较小的变形量,集中分布在浮环与鼓泡的接触区域,但不可避免地在非接触区域会产生较大变形,最大变形量为0.012 4 μm,其值也远小于浮环的厚度和鼓泡的高度。同时,浮环的最大等效应力值也是在浮环与鼓泡的接触区域,最大等效应力值为62.086 MPa,而鼓泡结构此处的最大等效应力值为59.045 MPa。本次分析柔性支承材料使用的是结构钢,具备屈服强度≥355 MPa,远大于62.086 MPa 的应力值。浮环变形量的值不高于0.02 μm,而柱面气膜密封的气膜间隙取为0.01 mm,气膜间隙大于浮环最大变形量。当柔性支承结构正常时,结构不会发生碰撞失效。
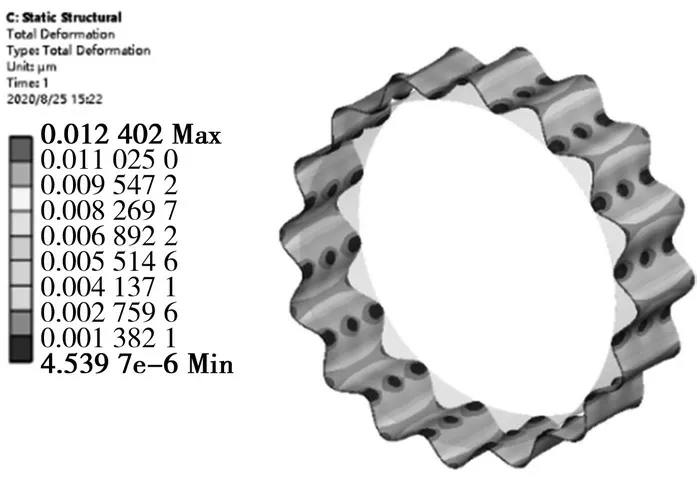
图11 浮环结构变形量云图Fig.11 Cloud diagram of maximum deformation of floating ring structure
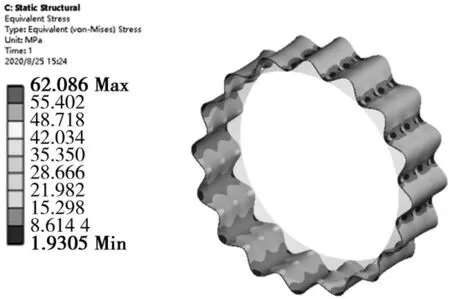
图12 浮环结构等效应力云图Fig.12 Equivalent stress cloud diagram of floating ring structure
3.2.1 平箔厚度对柔性支承性能的影响
根据控制变量法,在确保其他参数不变的情况下只改变单个参数。当鼓泡高度为0.25 mm、鼓泡半径为1 mm 时,分析平箔厚度变化对其柔性支承性能的影响。柔性支承的等效应力最大值、最大变形量的影响曲线图如图13 所示。

图13 平箔厚度对柔性支承性能的影响Fig.13 Influence of flat foil thickness on the performance of flexible support
由图13 可以分析得出,随着平箔厚度的增加,柔性支承的最大等效应力、最大变形量不断在减小。原因是平箔厚度变大会使柔性支承整体刚度变大,增大平箔的抗弯刚度,平箔结构在相同的外载荷下的变形减小,径向刚度增大,同时抑制了平箔变形引起的密封气体的流失,提高了气膜的刚度。而鼓泡结构的最大等效应力,随着平箔厚度的增加,基本不受其影响,保持在一个大致稳定的值。平箔结构最大变形量与平箔结构等效应力的变化趋势基本保持一致。
3.2.2 鼓泡高度对柔性支承性能的影响
由图14 可以看出,在控制其他变量不变的情况下,鼓泡高度增大,柔性支承结构最大等效应力出现了先增大后降低的变化趋势。鼓泡高度在0.2~0.3 mm 的高度时,平箔的最大等效应力值趋于平缓,而平箔的最大变形量,在鼓泡高度处于0.2~0.45 mm 范围内,几乎保持不变,鼓泡高度对平箔的变形量的影响相对较小。
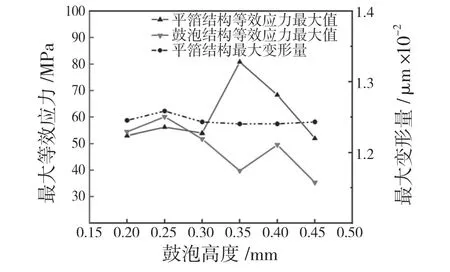
图14 鼓泡高度对柔性支承性能的影响Fig.14 Effect of bubble height on the performance of flexible support
3.2.3 鼓泡半径对柔性支承性能的影响
由图15 可以看出,在鼓泡高度取定0.25 mm时,鼓泡半径过小,平箔会产生较大的等效应力,半径过大,对比较小鼓泡半径的等效应力也没有明显的改善,考虑影响其结构设计的美观且加大了材料的使用,综上鼓泡半径取0.9~1 mm 较为合理。
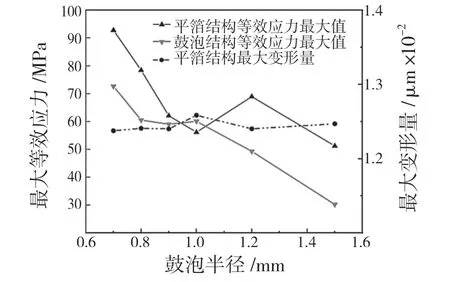
图15 鼓泡半径对柔性支承性能的影响Fig.15 Influence of bubble radius on the performance of flexible support
3.2.4 不同材料对柔性支承性能的影响
在相同的工况下,不同材料的平箔最大等效应力、变形量不同。石墨的最大变形量要明显高于其他材料,是因为石墨材料的密度小,弹性模量、泊松比较小,导致使用石墨材料时,具有较大的变形量、较小的等效应力。但石墨材料有着较好的自润滑性,在结构运行过程中发生碰磨的情况下,石墨粒由于自润滑性可减缓动环与浮环的摩擦,有利于气膜的稳定。而采用铍青铜材料的最大等效应力要明显大于钢材料以及碳化钨材料,最大变形量仅小于石墨材料。考虑到在柔性支承材料的选择中,要注重材料强度与刚度兼顾,铍青铜的等效应力较大而变形量适中,在5 种材料中性能最为合适。如图16、图17 所示。
4 结论
使用ANSYS 软件,对柱面气膜密封柔性支承结构进行单向流固耦合分析,得到了柔性支承结构等效应力和最大变形量情况。得到的相关结论如下:
(1)平箔厚度的变大使柔性支承整体刚度变大,使得柔性支承结构的承载力和抵抗变形能力变强。根据仿真结果发现,平箔厚度在0.6 mm以后,平箔结构的等效应力、最大变形量变化趋势变平缓,建议平箔厚度取值0.6 mm,可以使结构具有较好的强度和刚度。
(2)通过对柔性支承结构中平箔厚度、鼓泡半径、鼓泡高度几个参数的控制变量仿真,对柔性支承的最大等效应力和变形量进行分析发现,鼓泡结构的柔性支承可以很好地抵抗变形,平箔厚度对柔性支承影响最大,鼓泡半径、鼓泡高度对柔性支承相对较小,考虑取值鼓泡半径0.9~1 mm,鼓泡高度0.2~0.3 mm。
(3)通过对柔性支承结构进行仿真研究发现,鼓泡结构的柔性支承在产生合理的等效应力同时有较小的变形量可以很好地抵抗变形,能够满足柱面气膜密封的正常运行。柱面气膜密封鼓泡箔片的箔片变形分布与经典的波箔结构有类似之处,但也存在着明显的差异,鼓泡箔片的点支撑效应是这种差异存在的主要原因。

